Airport gate assignment problem with deep reinforcement learning①
Zhao Jiaming(趙家明),Wu Wenjun,Liu Zhiming,Han Changhao,Zhang Xuanyi,Zhang Yanhua
(*Faculty of Information Technology,Beijing University of Technology,Beijing 100124,P.R.China)(**IT Department,Beijing Capital International Airport Co.Ltd,Beijing 100124,P.R.China)
Abstract
Key words:airport gate assignment problem (AGAP),deep reinforcement learning (DRL),Markov decision process (MDP)
0 Introduction
In recent years,the air transportation has developed rapidly.However,this development has also brought great challenges to the operation and management of civil aviation.Airport is the terminal of any airline,bearing great pressures of the rapid growth of air traffic.The limited resources and operating abilities of airport has become one of the main causes of flight delays.In the airport operation,gates including fixed gates next to the terminal and remote gates located on apron are key resources.The gate assignment directly affects the airport operation efficiency and the quality of experience (QoE) of passengers.Therefore,the optimal assignment of gates plays an important role in practice.
In 1974,Steuart modelled the airport gate assignment problem (AGAP) for the first time[1].Dorndorf summarized the optimization objectives and constraints of the AGAP problem in 2007[2].As a result of his contribution,the academic research on AGAP has turned to the innovation of algorithm.The AGAP algorithms are mainly divided into 2 categories:mathematical programming algorithm and heuristic algorithm.The representative algorithms in the mathematical programming algorithm are the column generation method and the branch and bound algorithm.Both 2 algorithms were used to solve AGAP[3,4]and achieved some positive results.The advantage of mathematical programming algorithm is that it can be found the global optimal solution of the problem.Meanwhile,the shortage is also very obvious,i.e.these algorithms are only applicable to the AGAP with a small number of flights and gates due to their high complexity.The heuristic or modern heuristic algorithms are more popular in academics.The object such as minimizing the idle time of gates,reducing the number of flights that have not been assigned to gate,equalizing the idle time of aircraft,minimizing the distance traveled of passengers and the number of flights assigned to remote gate are considered.The greedy algorithm,genetic algorithm,Tabu search algorithm,bee colony algorithm and several other heuristic algorithms are used to solve these problems[5-9].Ref.[10] has also developed an airport gate assignment framework to deal with the issue of aircraft assignment under random flight delay and adopted a heuristic algorithm module to iteratively solve the AGAP problem.
Although researches have been carried out in the academia,the AGAP still faces many problems in practice.In most cases,the AGAP is divided into 2 stages in practice,i.e.the pre-assignment stage based on known flight plans and the dynamic assignment stage to adjust the random change of flight time.The existing algorithms can be used to solve the pre-assignment problems.However,the contradiction between the complexity of the existing algorithms and the timeliness of the dynamic assignment are both difficult problems.
In the development of artificial intelligence (AI),deep reinforcement learning (DRL) technology has received extensive attention[11,12],which can be applied to solve complex decision problems in various fields.In Ref.[13],DRL method was used to solve the problem of scheduling tasks with multiple resource demands.The results show that the proposed deep RM performs better than the heuristic algorithm and adapts to different conditions.This has significant implications for the research.AGAP is also a kind of task scheduling and resource assignment problem,in which tasks are flights and resources are the airport gates.The important point is that DRL based algorithm can satisfy the timeliness requirements of the dynamic AGAP.
In this research,a DRL based method to solve the AGAP with random flight delay is proposed.Considering the passenger’s QoE,the distance traveled of passengers is reduced by maximizing the ratio of flights assigned to fixed gates next to the terminal.The AGAP is translated into a Markov decision process (MDP) which can be solved as a learning problem.The proposed DRL based method is validated via simulation and the solution using the software Gurobi is given for comparison.Simulation results show that the optimization performances of the proposed method and Gurobi based solution are quite close.Meanwhile,based on the proposed method,the calculation speed of the trained airport gate assignment policy is much faster than that of the Gurobi based solution.This confirms that the proposed method can be used to solve the dynamic assignment problem in practice.The main contribution of this research is summarized as follows.
1) The MDP model of the dynamic AGAP is proposed with constrains of gate resources and time interval modeled in the states.
2) The DRL framework is adopted as the solution of the dynamic AGAP.Simulation results validate that the performance of the proposed DRL-AGAP method is close to that of the Gurobi optimization solver with extremely low computing complexity.
The rest of this paper is organized as follows.System model is presented in Section 1.In Section 2,an optimization problem for AGAP is formulated into an MDP.Then the problem solution via deep reinforcement learning is proposed in Section 3.Section 4 discusses the simulation results.Finally,the proposed method is concluded with future work in Section 5.
1 System model
In this work,the research is based on the AGAP with DRL.Before landing of a certain flight,the gate assignment agent will assign it to an available gate.The system model is described in Fig.1.The total number of flights and gates are denoted byNandM,respectively.The landing time of all the flights is based on a fixed schedule with random time fluctuation.Two types of gates are considered:fixed gates next to the terminal and remote gates located on apron.As an initial research on the AGAP with DRL,the simplest scenario is taken into consideration.Assuming the size of all the gates is the same and all the aircraft types are the same.And also assuming runway assignment has been made prior to the assignment of gates[14].Besides,the runway conflict is not considered in this initial research.
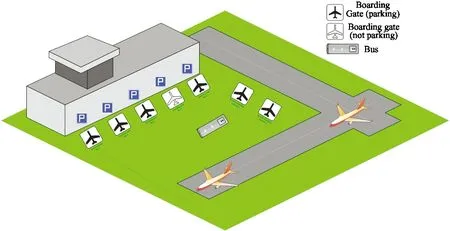
Fig.1 Example of airport gates assignment
1.1 Objective
Airport gate assignment is closely related to passenger’s QoE.In general,people prefer a shorter waiting time and a shorter walking distance after landing.Therefore,when the flight is assigned to the fixed gates,the passengers on the flight are satisfied the most.When the flight is assigned to the remote gates,passengers have to go back to the terminal by shuttle bus.Thus,the passengers are not satisfied and the operation cost is higher.Taking the QoE of passengers as the key operational indicators,the optimization object can be designed as maximizing the rate of flights assigned to fixed gates.The objective function can be calculated as
(1)
where,Y=[yij]N×Mis the assignment matrix and the optimization variable,g=(g1,g2,…,gj,…,gM) is the gate type vector.If flightiis assigned to the gatej,yij=1,otherwiseyij=0.If the gatejis a fixed gate,gj=1,otherwisegj=0.
1.2 Constraints
As the ideal scenario for AGAP is considered in this work,only the basic constraints are taken into account.
1) Each flight must be assigned to one and only one gate
(2)
where,Mis the total number of gates.This formula ensuresi-th could only be assigned to one gate.
2) Time interval constraint
Normally,flight takes some time in the process of entering and leaving the gate.When two or more flights are assigned in the same gate,there must be a certain interval constraint between the departure time of the previous flight and landing time of the next flight[15].According to Ref.[15],the next flight should be assigned to the gate at least 300 s after the departure of the previous one.It can be mathematically expressed as
yikyjk(lj-di-300)≥0
(3)
where,flightfiandfjare assigned to the same gatek,fiis earlier one,yik=yjk=1.ljis landing time offj,diis departure time offj.
3) 0/1 variable constraint
yij∈{0,1}
(4)
yijis the decision variable of AGAP.AGAP is modeled as a 0-1 programming problem.
1.3 AGAP optimization mode
According to the optimization objective and constraints given above,the optimization problem in this paper can be expressed as
yikyjk(lj-di-300)≥0
(5)
yij∈{0,1}
2 Markov decision process formulation of AGAP
The Markov decision process provides a mathematical architecture model for how to make decisions in a state where part of the randomness is partially controlled by the decision maker[16].As the arriving flow of flight is a sequence in time,the assignment decision for these flights must be made as discrete time series.Therefore,the real-time (dynamic) AGAP can be naturally modeled as a Markov decision process.In the rest of this section,the MDP formulation of AGAP and the definition of state space,action space,and rewards will be described.
2.1 State space
The state is formulated as a resource images denoted bySt.The resource view can be divided into two parts:gate image and fight image.
As shown in Fig.2,the horizontal axis represents the gate resources,and the vertical axis represents the time steps.The gate image represents the gate resource occupancy and the available gate resources from current time to aTmaxtime steps in the future.The flight image represents duration between the landing time and the departure time of the next several flights.To simplify the expression of the state,the safety interval is also included in the duration.Besides,the occupied gates are marked in the flight image by colored,which will be updated at each time step after gate assignment.
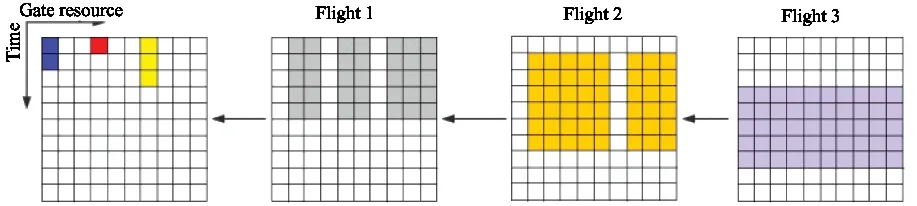
Fig.2 An example of state representation,with gate resources and 3 pending flights
More specifically,taking the colorful image in Fig.2 as an example,the different colors in these images represent different flights.At the current time step,gates 1,4 and 7 are occupied.The blue colored flight is assigned to gate 1 and will still stay in gate 1 for two more time steps.The flight images represent the gate resource requirements of awaiting flights.Flight 1 requires to stay for 5 time steps and there are 7 available gates for it currently.
2.2 Action space
Theoretically,if the flights information remains unchanged during the experimental time,the agent can decide the gates assignment for theNflights at the same time and the size of action space isMN.However,due to the random time fluctuation of the landing time,only the predicted landing time of the upcoming flight is accurate.Thus the dynamic AGAP discussed in this paper is more accurate and practical.As a result,for dynamic AGAP,agent only assigns the first awaiting flight to an available gate,and the size of the action space is greatly reduced toM.The action can be denoted byAt∈{1,2,3,…,M-1,M},whereAt=imeans to assign the first awaiting flight to thei-th gate.
2.3 State transition
When an action has been selected,it will changes the state.Fig.3 shows how the state is affected by the action.In the first row of images,Flight 1 is the first awaiting flight to be assigned.According to the gate image,Fight 1 can not be assigned to gate 1,4 and 7.Flight 2 is the second awaiting flight.According to the image,it will arrive 2 time steps later and leave 7 time steps later.During that time,only gate 1,7 are occupied,gate 4 will be available.If the agent selects gate 2 for Flight 1,the state will change to the images in the second row.Gate 2 will be occupied and the flight images are changed accordingly.
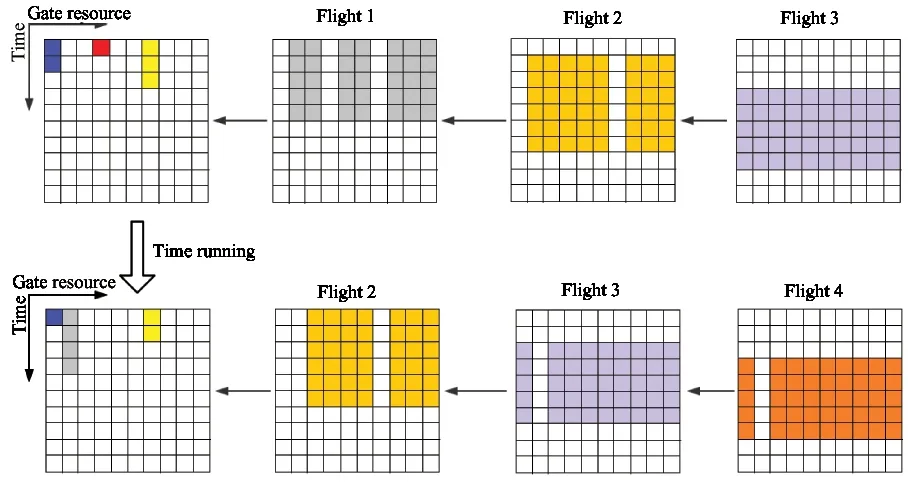
Fig.3 An example of state transition
2.4 Rewards
As mentioned in Section 1,the proposed objective is to maximize the rate of flights assigned to fixed gates.The rewardRis set asRbwhen the flight is assigned to the fixed gate;Rgwhen assigned to the remote gate.The relationship thatRb>Rgis satisfied,which ensures that the agent tends to assigned more flights to the fixed gates.
According to the definition of value of state in reinforcement learning and the definition of the equivalent optimization objective in Eq.(5),the value of the initial stateS0can be calculated as
(7)
where,γis the discount factor andRtis the reward of time stept.Ifγ=1,the reward at time steptcan be calculated as
Rt=gAt
(8)
whereAtis the selected action at time stept.
3 Deep reinforcement learning based problem solution
As the state transition of the MDP of AGAP is quite complicated,a DRL based method is proposed to solve the dynamic AGAP called DRL-AGAP.The policy which the agent uses to make gate assignment decision is designed as a deep neural network (DNN) denoted by πθ.The AGAP is transformed to a DRL problem and the major work is to train the policy network.The framework of DRL-AGAP is given in Fig.4.

Fig.4 The framework of DRL-AGAP
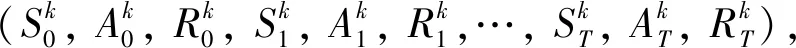
More detailed information of the policy gradient method used can be found in Ref.[13].In Algorithm 1,the process of one time step in the episodic simulation is detailed.

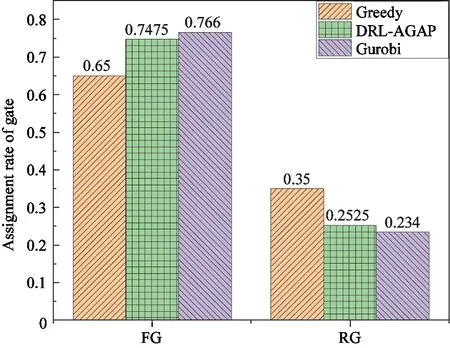
Algorithm1 Simulationprocessofk-thepisodeofj-thflightschedulesStart: Step1:InitializestateSk0. Step2:t=0 Step3:Whetherthereisaflightinthestateoftheflight,ifthereisaflightgotoStep4,otherwisegotoStep8. Step4:InputSktintopolicynetworkπθ,calculatetheas-signmentprobabilityp=(p1,p2,…,pM)ofthefirstflightintheflightstate. Step5:Deleteunavailablegatesinp.Availablegatesprobabilityisp′. Step6:Chooseagateaccordingtop′asAkt. Step7:CalculateRkt,andstore(Skt,Akt,Rkt). Step8:t=t+1 Step9:Ift In this section,the simulation results of the proposed DRL-AGAP method will be introduced.As an initial research,a neural network is built with a fully connected hidden layer with 200 neurons,which is the policy network.The maximum visible time steps of the resource view isTmax=20.Each time step is set to be 5 min in practice,so that resource view can cover 2 h.It is definedM=202 gates at an experimental airport and about 35% of them are fixed gates.The number of flights in each flight schedule isN=400 which lasts for one day.And 100 flight schedules are generated as training sample which means 40 000 flights data would be trained as an sample.The maximum simulation time of each episode is set asT=400 time steps.In each training literation,four episodic simulations are run for each flight schedule.Due to the characteristics of the problem,the step size of the gradient drop cannot be too large.If it is too large,the gradient will disappear.Learning rate is set as 0.0001.After the simulation of 500 iterations,the algorithm converges. We compared the performance of the proposed DRL-AGAP with 2 methods:Greedy and Guorbi.Greedy is the traditional algorithm to solve AGAP.For the current flights,it is assigned to the available fixed gate,regardless of its impact on subsequent flights.Gurobi is a new generation of large-scale mathematical programming optimizer developed by Gurobi Corporation[17].This software is an advanced method to solve AGAP at present.When using this optimization software,the AGAP is modelled as a mathematical programming problem.It is also worth noting that the AGAP solved by software Gurobi is a pre-assignment problem which assigns 400 flights at one time. Firstly,the performance of convergence is evaluated.The sample flight schedules the software Gurobi used to test the optimization performance are the same as the training samples of DRL-AGAP. As shown in Fig.5,the lines indicate the trend of the training process of the policy network.The original policy is a random assignment policy,with which only 35% of flights are assigned to the fixed gates (FG) and the rest 65% of flights are assigned to the remote gates (RG).After about 300 iterations of training,the ratio of flights assigned to FG has increased to more than 70%,which means the improvement of optimization objective is more than 100%.And the RG assignment rate reaches 28%.The range of discount is about 50% which means DRL-AGAP agent can converge the assignment result to the ideal result after training. From Fig.5,the optimized ratio of flights assigned to FG of optimization software Gurobi is slightly higher than the DRL-AGAP method.However,this is a very normal difference between the optimized performance of the global optimization method and the local dynamic optimization method.Generally,the global optimization result can be considered as an upper bound,and the proposed DRL-AGAP method can closely achieve this upper bound.The advantage of the DRL-AGAP is that it can adapt to different flight schedules when the policy network has been trained. Fig.5 Training performance comparation There are 100 new flight schedules generated to test the effectiveness of the policy network.As shown in Fig.6,the average FG assignment rate of DRL-AGAP is about 75%,and the average RG assignment rate of DRL-AGAP is about 28%.Compared with Greedy,the FG assignment rate is increased by nearly 10%,and the RG assignment rate is decreased by nearly 7%.Results also show that the ratio of flights assigned to FG using DRL-AGAP method is only 2% less than that using Gurobi.This is the same as the converged training performance.Meanwhile,the efficiency of using the proposed DRL-AGAP method is much better than using the software Gurobi.During the test,the assignment of 400 flights only needs to cost 29.29 s.But with Gurobi,for each new flight schedule,the global re-initialization is required which takes 1 910.49 s.The calculation speed has been increased by more than 65 times using DRL-AGAP.Calculation speed of the algorithm is improved. Fig.6 Test performance comparation Furthermore,the optimization software Gurobi models the problem as an optimization problem,which can only be pre-assigned according to the flight schedule.The DRL-AGAP proposed in this work models the problem as a Markov decision process,which can assign the gate dynamically according to current flights. In this work,a DRL-AGAP method is proposed to deal with the dynamic AGAP in practice.The dynamic AGAP is modelled as an MDP to ensure real-time decision making.The optimization objective is designed as maximizing the rate of flights assigned to the fixed gates.Simulation results confirm that the proposed DRL-AGAP can significantly increase the optimization objective.Compared with the optimization software Gurobi,the optimization results are close.Meanwhile,the computational cost of the proposed DRL-AGAP is much less than that of Gurobi,which can be used as a real-time dynamic assignment method.As an initial research on AGAP with DRL,the ideal scenario is taken into consideration to validate the feasibility and the effectiveness of the method.In the future,more accurate constraints in practice will be considered to make this kind of DRL based methods actually usable and meet the real operational needs of airports.4 Simulation results

5 Conclusions
 High Technology Letters2020年1期
High Technology Letters2020年1期
- High Technology Letters的其它文章
- Model-free adaptive control of space manipulator under different gravity environment①
- A bibliometric analysis of gene editing research①
- Optimization of yield criterion and simulation based on QP980 high strength steel①
- Exploring serverless computing for stream analytic①
- A 16-channel high-voltage reconfigurable and flexible-controlled implantable wireless closed-loop system for SCI repair①
- Robustness-supported user association and small cell switching ON/OFF strategies in 5G mm-wave networks①
