MULTIPLE JEEPS PROBLEM WITH CONTAINER RESTRICTION?
Xiangying HUA(華香穎)
Center for Mathematical Sciences,School of Science,Wuhan University of Technology,Wuhan 430070,China
E-mail:huaxiangying@whut.edu.cn
Abstract Jeep problem is a kind of model of logistics in extreme situation,which has application in exploration and aircraft problems.The optimal distance and driving strategy of multiple jeeps problem are known.We consider multiple jeeps problem with container restriction,which is more complicated in the proof of feasibility and optimality of a driving strategy.We investigate when it can achieve the same optimal distance as without restriction.Based on the non-restricted optimal distance,a new driving strategy is proposed.We provide the necessary and sufficient condition to ensure the feasibility of the strategy,and obtain the maximal feasible distance.
Key words jeep problem;caravan;container restriction;driving strategy
1 Introduction
The earliest problem that closely relates to jeep problem is Alcuin’s camel problem,which was first mentioned in a collection of mathematical problems in Latin by Alcuin of York[14].In 1947,Fine[7]introduced and solved a jeep problem of maximizing the distance a jeep can travel into the desert using n drums of fuel.Subsequently,Phipps[15],Alway[1],Gale[9]and Hausrath et al.[10]gave other solutions to the original problem or related problems.In each of the above problems the jeep can carry exactly one drum of fuel.Using one drum of fuel,the jeep can travel one unit of distance.It is implicit that the jeep can store whatever fraction of a drum of fuel at any point in the desert.Ding and Fan[5]introduced the optimal sequence method and used it in solving jeep-fuel station problems[6].Exploration problem and aircraft problem are similar to jeep problems[12,13,16].Moreover,jeep problem can be regarded as mathematical models for some practical problem such as interplanetary adventure,long-distance travel of unmanned aerial vehicle and multistage rocket travel,etc.
In 1987,Dewdney[4]proposed following Desert Fox problem:a jeep can carry one drum of fuel in addition to the fuel in its tank,fuel can only be stored in jeeps’s tank or in a drum,maximize the distance the jeep can travel in desert if there are n drums of fuel.In this case,the jeep has multiple loads(a tank and a drum,the drum is bigger than the tank),and a container restriction is imposed:fuel can only be stored in tank and in containers taken by the jeep from start point.In 1993,Jackson,Mitchem and Schmeichel extended Dewdney’s problem and gave an optimal algorithm[11].Recently,single jeep problem with container restriction was also studied by[3],it showed that a jeep can cross a desert of arbitrary length even with container restriction provided there are enough fuel at the start point.In[3],container and tank are equivalent and jeep can take more than one containers.So the problem in[3]is more fl exible than that in[11].In fact,given the same amount of fuel,the optimal distance of problem in[11]will not exceed it in[3].
A group of jeeps is called a caravan,the maximal distance a caravan can travel is de fined as the maximal distance that any jeep in the caravan can achieve.We consider the following caravan J(k,m,s):There are k jeeps and m of them are allowed not to return.Each jeep can carry a maximum load of s containers.Each container can contain one unit of fuel at most.One jeep travels one unit of distance per unit of fuel.
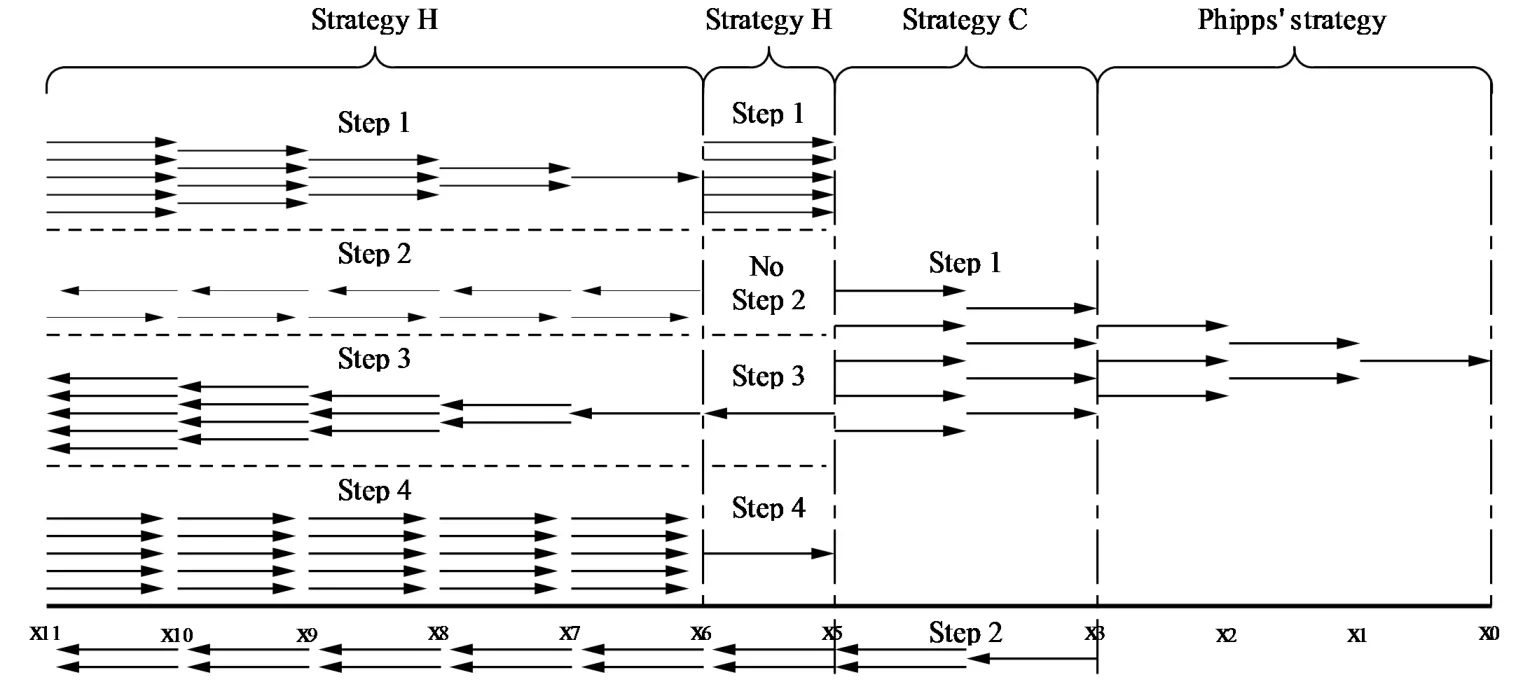
Problem 1.1(Multiple jeeps problem without container restriction)Given sp+f units of fuel at start point S,where p is a nonnegative integer and 0 ≤ f Chen,Ding and Fan obtained the optimal distance(p+f,m)and the driving strategy in[2].We are interested in multiple jeeps problem with container restriction.In this case,fuel can only be stored in the containers which are taken by the jeeps from the start point.Such kind of restriction has practical signi fi cance.For example,astronavigation fuel can only be stored in speci fi c containers and electric energy can only be stored in batteries. Problem 1.2(Multiple jeeps problem with container restriction)Given sp+f units of fuel at start point S where p is a nonnegative integer and 0≤f As previous driving strategies may no longer be feasible and the trouble in the proof of optimality of a feasible strategy,it is difficult to give optimal distance for Problem 1.2.Observe that(sp+f,m)≤(sp+f,m),an interesting question is in which case(sp+f,m)=(sp+f,m).In this note,we introduce driving Strategy H for Problem 1.2 so that(sp,m)=(sp,m)in some situations.For the case that 2k?m≤s,the maximal p such that(sp,m)=(sp,m)is s+k?1+?.For the case that 2k?m≥3s?4,the maximalj p isFor the case that s<2k? m<3s?4,the maximal p isThe proof of the first two cases is simpler.The arrangement of Strategy H in these two cases is intuitionistic.For the last case,it is more complex.To give the proof of the last case,we first give two lemmas.The first lemma excludes a case that will not happen when s<2k?m<3s?4.To prove this lemma,we discuss the possible value of the decimal part of some variables.The second lemma gives two inequations which will be used in the proof of the maximality of the p we give.We prove this lemma by constructing some equations. We fi x some terms for convenience.The travel starts at point S and finishes at point F.F is on the right of S.Driving towards F is called driving forwards.For any integer u with 0≤u≤p,let xudenote the point on segment SF such that the total consumption of fuel on the right of xuis su units.We use xηxθto denote the segment between xηand xθ,the length between them is also denoted by xηxθfor convenience.For any real number a,?a?denotes the maximal integer that no greater than a,?a?denotes the minimal integer that no less than a,{a}denotes the decimal part of a. Theorem 2.1(see[2])The maximal distance the caravan can travel in Problem 1.1 is Theorem 2.1 is just Theorem 3 in[2],if we consider s units of fuel as a new unit of fuel and s units of length as a new unit of length.In this case,when u ≥ m,andwhen 0≤u Now we give a travel strategy that achieves the optimal distance for f=0.The case f 6=0 is similar.There are three stages in the journey. Step 1The first stage is from the start point S(namely,xp)to xk.The strategy is provided by Chen,Ding and Fan[2].For each u with k≤u≤p?1,at xu+1,do the following operations.Repeat u+1?k times:at xu+1,choose one jeep take s units of fuel drive forward to xu;at xu,let it takeunits of fuel and drive backward to xu+1.After that,at xu+1,let all the k jeeps leave with full load and driveunits forwards to xu.As a result,at xu,there are u+units of fuel.Storeunits of fuel for future return of k?m jeeps. Step 2The second stage is from xkto xm.The strategy is provided by Chen,Ding and Fan[2].For each u with m≤u≤k?1,at xu+1,let u+1 jeeps leave with full load and drive forwards to xu.At xu,choose one jeep,storeunit of its fuel at xu,takeunits of its fuel to other u jeeps so that they are full load and will travel forward.Let the chosen jeep use the remainingunits of fuel drive backward to xu,and use the fuel stored at xu+1,···,xp?1return to S. Step 3The third stage is from xmto F(namely,x0).The strategy is provided by Phipps[15].For each u with 0≤u≤m?1,at xu+1,let u+1 jeeps take full load and drive to xu.At xu,choose one jeep,put all of its restunits of fuel into other u jeeps so that they are full load.When u=0,the last jeep will arrive at the finish point F. Let Pudenote any point on segment xu+1xufor all integer u.From the travel strategy of Theorem 2.1 and the proof of Theorem 3 in[2],a strategy can achieve the optimal distance in Problem 1.1 if and only if it is feasible and Puis crossed the same times as it in above strategy.In fact,to achieve the maximal distance(sp+f,m),a travel strategy should satisfy the following two rules: Rule on Cross TimesIf u≤m?1,jeeps only go forward and Puis crossed by jeeps u+1 times.If u≥m,Puis crossed u+1 times when jeeps go forward,and is crossed u+1?m times when jeeps drive backward. Rule on LoadsAny jeep should be full load when it leaves xu+1and goes forward to xu.The fuel a jeep carry should just run out when it leaves xuand travels backward to xu+1. As the existence of container restriction,if(sp+f,m)=(sp+f,m),it must be the optimal distance.An interesting question is under which condition The following example illustrates how the container restriction a ff ects a driving strategy. Example 3.1For the caravan J(3,1,4)in Problem 1.2 with p=5. In this problem,there are 20(sp=4?5)units of fuel in 20 containers at start point.There are three jeeps in the caravan and one of them is allowed not to return.Each jeep can carry four containers. We now try to apply the strategy mentioned after Theorem 2.1.At x5,let a jeep leave and go forward with full load.When it arrives at x4,it remains 32/9 units of fuel.Then we need to build a storage at x4with 28/9 units of fuel.And the jeep need to drive backwards to x5with 4/9 units of fuel.The storage needs 4 containers while the jeeps need 1 container.Thus,there should be at least 5 containers at x4.But when the jeep comes,it bring just 4 containers.So the containers are not enough,and the strategy is unfeasible. Proposition 3.2If sp+f≤sk,then(sp+f,m)=(sp+f,m). ProofIf sp+f ≤ sm,it is easy to see that Phipps’strategy is feasible and When sm Step 1At xk,let all the k jeeps leave with full load and go forward.Each time the caravan cross an xuwhere m Step 2At xm,choose one jeep and take fuel from it to make other m jeeps full load.The m jeeps will continue to go forward using Phipps’s strategy and eventually one of them will arrive at F.Let the chosen jeep use remainingunits of fuel return to xm+1,and use fuel taken from storage jeeps at xm+1,xm+2,···,xk?1return to S by Rule on Loads.Storage jeeps go back to S by the same way. In Strategy C,jeeps just carry bucketful of fuel or transfer fuel from some containers to other containers.So Strategy C will not be af f ected by container restriction and it is feasible. Remark 3.3The conclusion in Proposition 3.2 does not depend on s.In the restricted single jeep problem considered in[3],when s=1,one obtains(sp+f,m)<(sp+f,m)on the left of x1.That is to say,with container restriction,increasing the scale of caravan is benef i cial.When sm Remark 3.4If there are some strategies applied on the left of xk(that is,the start point of the whole travel is on the left of xk),then after Strategy C,there are k?m jeeps at xkshould drive back to S.In this case,if the strategy that used on the left of xkis feasible,there will remain fuel at storages between S and xkby which the k?m jeeps can drive back to S. We now give a strategy called Strategy H that is helpful to realize(sp+f,m)=(sp+f,m)when sp+f>sk.Strategy H is applied on the left of xk.We just describe the operation for f=0,the case that f 6=0 is similar.We emphasise that although Strategy H is used on the left of xk,it is not directly applied on Sxk.In fact,in many cases,we have to divide Sxkinto small parts and apply Strategy H on each part.Without loss of generality,we describe Strategy H on segment xtxt?γ,where t≤p and γ≤k≤t?γ.Notice that t≤p and t?γ≥k indicate that segment xtxt?γis part of Sxk.And γ≤k means that the amount of jeeps that Strategy H can deploy may not exceed k.The length of xu+1xuin Strategy H iswhich is same as in(sp+f,m). Now we describe Strategy H which consists of four steps. Step 1At xt,let all the k jeeps leave and go forward.Each time the caravan cross an xufor all u that t?γ Step 2At xt?γ,if t?γ>k(namely,xt?γis not xk),choose one jeep to travel between xt?γand xtfor t?γ?k times.During this process,the chosen jeep takes fuel from xt,xt?γand storage jeeps according to the Rule of Loads given in the end of Section 2.As a result,more containers and fuel can be moved from xtto xt?γ,and the fuel at storage will be reduced. Step 3At xt?γ,let one jeep takeunits of fuel return to xt?γ+1,and use fuel taken from storage jeeps at xt?γ+1,xt?γ+2,···,xt?1return to xtby Rule on Loads.Storage jeeps go back to xtby the same way.The remaining fuel at xt?γ+1,xt?γ+2,···,xt?1form storages. Step 4At xt,let all the γ jeeps leave and drive forward with full load.Each time they cross a storage,take fuel from storage to make them full load.Now all the k jeeps have arrived at xt?γ.The rest fuel that stored at storages is prepared for the future return journey of k?m jeeps. Remark 3.5As the length of xu+1xuis same as in(sp+f,m),if Strategy H is feasible on Sxk,then(sp+f,m)=(sp+f,m).But Strategy H is not always feasible,we will show under what condition Strategy H is feasible in Theorem 3.13.Note that in Strategy H,when jeeps go forward,they just carry containers with fuel or take fuel from storage to make themselves full load.So container restriction does not a ff ect Strategy H when jeeps go forward.When jeeps drive backward,sometimes fuel and containers will be reallocated between jeeps and storages.So container restriction may a ff ect Strategy H only when jeeps drive backward. We give an example and illustrate how Strategy C and Strategy H are used in a journey to realize(sp,m)=(sp,m). Example 3.6Consider the caravan J(5,3,6)with p=11 in Problem 1.2. In this case,there are 66 units of fuel in 66 containers at start point.There are fi ve jeeps in the caravan and three of them are allowed not to return.Each jeep can carry six containers.The whole journey for the caravan to realize(66,3)=(66,3)is illustrated in Figure 1. Figure 1 The journey for Example 3.6.The whole journey consists 4 parts(Strategy H on x11x6,Strategy H again on x6x5,Strategy C on x5x3,and Phipps’strategy on x3x0)as well as the return trip of 2 jeeps.One can check the whole journey is feasible.In the strategies we used,(66,3)=(66,3)which indicates that xu+1xu= when u≥m and xu+1xu= when u Now we give the necessary and sufficient condition under which the container restriction takes e ff ect for strategies aim at(sp+f,m)in some special situation. Suppose there are b containers and c units of fuel at a place B.As fuel can only be stored in container,we have c≤b.There are g jeeps going to leave B to A,and the distance between A and B is d.As g jeeps need dg units of fuel and a jeep should carry at least one container,we know that b≥g and c≥dg. Lemma 3.7Under container restriction,when d≤1,the journey that g jeeps leave B to A is feasible if and only if c?gd≤b?g.When d>1,the journey that g jeeps leave B to A is feasible if and only if c?gd ≤ ?b? gd?. ProofThe proofs of the cases that d≤1 and d>1 are similar.So we just give the proof of the first case. If d≤1,g containers can store gd units of fuel.So if g jeeps have leaved B,gd units of fuel and at least g containers have been taken away.Thus,there are c?gd units of fuel and at most b?g containers at B.The rest fuel must be stored in containers,we obtain c?gd≤b?g. If c?gd≤b?g,then c?gd units of fuel can be stored in b?g containers.As d≤1,gd units of fuel can be stored in g containers.It allows g jeeps leave B with gd units of fuel and g containers.And it allows the remaining c?gd units of fuel at B be stored in remaining b?g containers. Corollary 3.8Suppose the distance between place C and place D is d.There is a caravan leaving C with full load and arrive at D.And some jeeps in the caravan need to drive back to C with fuel that just fi t the need of their travel.Then with container restriction,the journey is feasible if. Corollary 3.8 is a direct consequence of Lemma 3.7. 3.3.1The Feasibility of Strategy H Now we focus on the feasibility of Strategy H.The length of xu+1xuin Strategy H iswhich is the same as in(sp+f,m).So if it is feasible,(sp+f,m)=(sp+f,m).Now we consider the condition under which Strategy H is feasible.We will apply Strategy H on segment xpxp?γ,where γ is a positive integer.As Strategy H is used on the left of xk,we obtain that p?γ≥k.According to the first step of Strategy H,we have γ≤k.Note that the rightmost segment in xpxp?γis xp?γ+1xp?γ.Put Theorem 3.9In Problem 1.2,if Strategy H can be applied on segment xpxp?γ,namely,p?γ≥k≥γ,we have the following facts. 1.Strategy H is feasible on xpxp?γif and only if ? ≥ 1. 2.If Strategy H is feasible on xpxp?γ,it is also feasible on xu+1xufor all u that k≤ u ≤p?γ?1,namely,(sp,m)=(sp,m). ProofWe emphasise again that the length of xu+1xuisin Strategy H. 1.First,consider the case thatfor all β with 0 ≤ β ≤ γ ? 1,that is,the length of arbitrary xu+1xuis no less than 1/2 if xu+1xuis a part of segment xpxp?γ.By Corollary 3.8,it can be easily seen that Strategy H is feasible on xpxp?γ.Asand γ ≤ k,simple calculation implies ? ≥ 1 holds. Second,consider the case thatfor all β with 0 ≤ β ≤ γ ? 1,that is,the length of arbitrary xu+1xuis less than 1/2 if xu+1xuis a part of segment xpxp?γ.From Remark 3.5,to prove the feasibility of Strategy H we just need to focus on the processes that jeeps drive backward.So in Strategy H we just need to focus on Step 2 and Step 3.We discuss container restriction for xp?γand for xp?γ+β(1 ≤ β ≤ γ ?1)respectively.At xp?γ,there are p?γ?k+1 times that reallocating containers and fuel(p?γ?k times in Step 2 and one time in Step 3).By Lemma 3.7,the ith leaving is feasible if and only if The number on the right hand side of the inequality sign in(3.3)is i because there are at least i?1 containers have been taken away when the ith leaving takes place.The restriction(3.3)gets stricter as i increase.We consider the worst case i=p?γ?k+1,under which(3.3)is equivalent to ? ≥ 1.Then we look at xp?γ+β.For each β,there is only one time that reallocating containers and fuel at xp?γ+β.By Lemma 3.7,Strategy H will not be a ff ected by restriction at xp?γ+βif and only if Restriction(3.4)gets stricter as β decrease.Direct calculation implies the restriction ? ≥ 1 is stricter than(3.4)when β =1.Thus,? ≥ 1 holds if Strategy H is feasible on xpxp?γ. Finally,consider the case thatfor some β andfor other β with 0 ≤ β ≤ γ ? 1,that is,if xu+1xuis a part of segment xpxp?γ,the length of it may be no less than 1/2 as well as may be less than 1/2.By Corollary 3.8,it can be easily seen that those segments on xpxp?γwhose length are no less than 1/2 will not be a ff ected by container restriction.Now,we focus on those segments whose length are less than 1/2.Similar to the discussion we have in the case thatfor all β,Strategy H will not be a ff ected by restriction at xp?γ+βif and only if(3.4)holds,and restriction(3.4)gets stricter as β decrease.Suppose xp?γ+β? is the point on segment xpxp?γthat the length of segments on the right of it are no less than 1/2 and the length of segments on the left of it are less than 1/2.Then xp?γ+β? is the point whose restriction(3.4)is the strictest.Restriction(3.4)at xp?γ+β?is According to the de finition of β?,there is,by which we have According to γ ≤ k ≤ p?γ and β?≥ 1,we have Combining(3.6)and(3.7)we can conclude(3.5)holds.Thus,all segments whose length are less than 1/2 will not be a ff ected by container restriction and Strategy H is feasible.And simple calculation implies ?≥1. From the discussions we have above,we conclude the necessity of ?≥1.And the sufficiency of ?≥1 can also be concluded according to the disscussions.Thus we know Strategy H is feasible on xpxp?γif and only if ? ≥ 1. Remark 3.10From the proof of Theorem 3.9,Strategy H is feasible only when s≥2. 3.3.2The Maximal Capacity of Strategy H By Theorem 3.9 we know the condition under which Strategy H is feasible.Now we concern about the maximal capacity of Strategy H.That is,what is the maximal p such that Strategy H can make(sp,m)=(sp,m).To make our expression concise,let then we have here α is the integer part ofand β is the integer part of,A is the decimal part ofand B is the decimal part of We first give two lemmas which are useful in the proof of the maximal capacity of Strategy H. Lemma 3.11A+B 6=1 if A in(3.11)and B in(3.12)are nonzero. ProofWe use reduction to absurdity.Asit is easy to see that when B 6=0,there isoror. According to(3.14)we have Combine(3.15)and(3.16),we have In(3.17), α and β are integers,so on the right of equal sign the numerator(4β +1)2is odd and the denominator 8(α+β+1)is even,which means s is not an integer.However,in jeep problem,s is the maximal quantity of containers that each jeep can take and s is an integer.Thus,we get an absurdity about s,which indicates that A+B 6=1 when B=. and s is not an integer.Thus,we get an absurdity about s,which indicates that A+B 6=1 when B=. and s is not an integer.Thus,we get an absurdity about s,which indicates that A+B 6=1 when B=. Lemma 3.12If A+B>1,we have ProofLet then we have where δ is the integer part ofand D is the decimal part of.As we have By(3.25)and(3.26)we know δ= α+β+1 when A+B>1,and For(3.20),we have For(3.21),we have we have By(3.26)and(3.31)we know 2sD is an integer when A+B>1,namely,8sD≥4.Combining(3.27)we have 8s(A+B)≥8s+4 holds,so(3.20)and(3.21)hold. Now we can give the maximal capacity of Strategy H. Theorem 3.13Suppose P is the maximal p such that(sp,m)=(sp,m)by Strategy H,then we have ProofFrom Theorem 3.9 we know P is the maximal integer p such that ?≥1.Now we f i nd the maximal p satis fies ? ≥ 1.When finding p and γ,there are three restrictions.The first is ?≥1,which is the result of Theorem 3.9.The second is p?γ≥k,which means that xpxp?γis on the left of xk.The last one is γ ≤ k,which means that the amount of jeeps that Strategy H can use not exceeds the amount of jeeps in the caravan.Especially,for the first restriction,if the other two restrictions are satis fied,then ?≥1 is equivalent to As ?≥1 is equivalent to Thus,the first restriction is equivalent to Let simple calculation implies that f′(γ)=0 when γ = γ??,f′(γ)>0 when γ > γ??and f′(γ)<0 when γ < γ??.Thus,f(γ)gets maximum when γ = γ??. 1.When 2k ? m ≤ s,simple calculation implies γ??≥ k.Combing(3.35)we know p ≤?.Thus,if there exists an integer γ such that the three restrictions hold with p=,then ?f(k)?is the P we are finding.In fact,the γ exists and γ =k.Simple calculation implies that γ =k and p= ?f(k)?satisfy the three restrictions.So when 2k?m ≤ s,P==s+k ?1+??. 2.When 2k?m≥3s?4,the first restriction requires(3.35)holds and the second restriction requires p≥k+γ,so there is a necessary condition that the first and the second restrictions hold at the same time: Under the condition that 2k?m≥3s?4,(3.37)is equal to Simple calculation implies γ?≤ γ??.Combing(3.35)we know p ≤.Thus,if there exist an integer γ such that the three restrictions hold with,then?is the P we are finding.In fact,the γ exists andNow we give the reason why ?γ??is the γ we are finding.Notice that If γ?is an integer,combining(3.39)we have?=f(γ?).Then simple calculation implies the three restrictions hold.If γ?is not an integer,simple calculation implies that f′(γ) ≤ 1 when γ ≤ γ?.Thus we have namely, (3.39)shows that Combining(3.41)and(3.42)we have,namely,the first restriction holds.Combining(3.39),simple calculation shows that the other two restrictions hold.So when 3.When s<2k ? m<3s ? 4,from(3.35)we knowThus,if there exist an integer γ such that the three restrictions hold with,thenis the P we are finding.In fact,the γ exists.Let then simple calculation implies{γ??}=A.We affirm that ? γ = γ1= γ2when A=0, ? γ=γ1when A 6=0 and A+B<1, ? γ=γ2when A 6=0,A+B>1 and B=, ? γ = γ1and γ2when A 6=0,A+B>1 and B=, ? γ=γ1when A 6=0,A+B>1 and B=. As B 6=0 when A 6=0 and A+B>0,then by Lemma 3.11 we know A+B 6=1.Thus,the fi ve cases we give contain all the possibilities of the value of A and B.Now we give the reason why the γ and p=?satisfy the three restrictions. Now we discuss the first restriction.If A=0,then γ??is an integer and γ = γ??= γ1= γ2.Thus,(3.35)holds and the first restriction holds.If A 6=0 and A+B<1,then γ??is not an integer,andSimple calculation implies and By(3.45)we know combining(3.44)and(3.46)we have p and Combining(3.47),(3.48)and(3.20)we know(3.35)holds and the first restriction holds.Similarly,if A 6=0,A+B>1 and B=or,(3.47)gives p and(3.45)gives f(γ1).Combining(3.47),(3.45)and(3.21)we know(3.35)holds and the first restriction holds.Thus,for all the possibilities of the value of A and B,the first restriction holds. Now we discuss the second restriction.If γ takes γ1,we have When 2k?m<3s?4,we have namely, Combing(3.49)and(3.51)we know Thus,the second restriction holds.If γ takes γ2,we knowand Similar to the discussion we have in the case that γ takes γ1,by(3.51)and(3.53),we know namely,the second restriction holds.Thus,for all the possibilities of the value of γ,the second restriction holds. Now we discuss the third restriction.As γ??2 Multiple Jeeps Problem Without Container Restriction
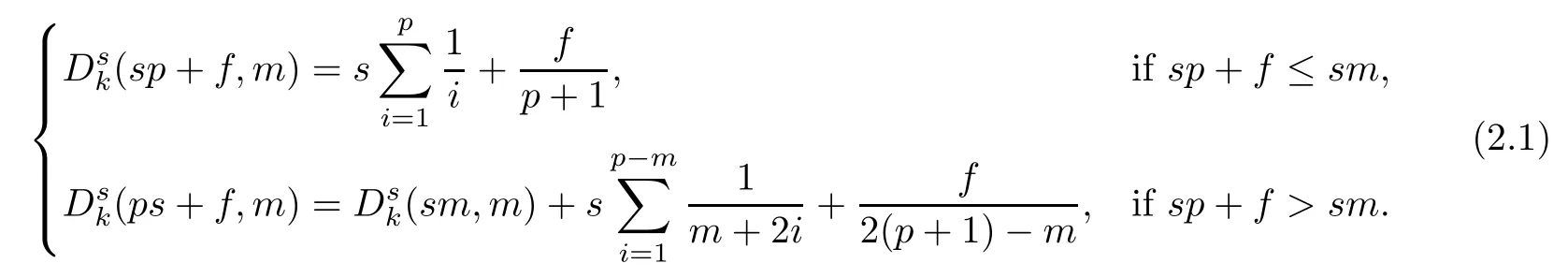
3 Multiple Jeeps Problem with Container Restriction
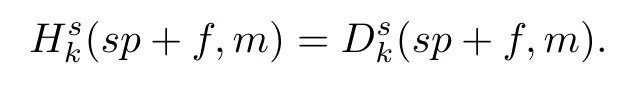
3.1 The Case that sp+f≤sk
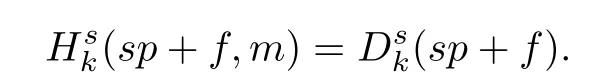
3.2 The Case that sp+f>sk:Strategy H
3.3 The Case that sp+f>sk:the Feasibility and Maximal Capacity of Strategy H
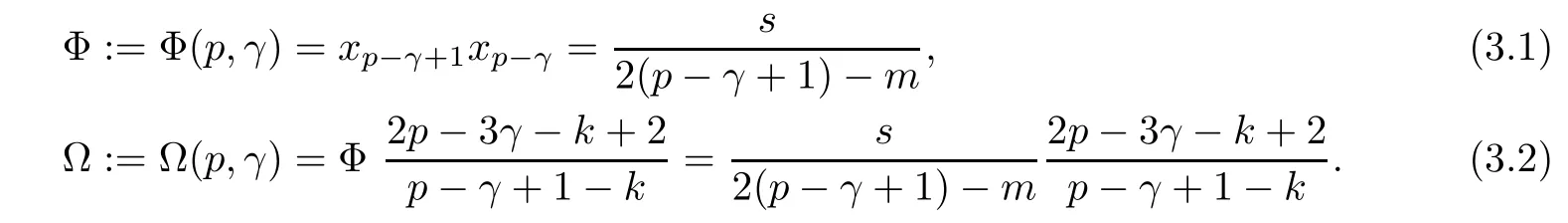
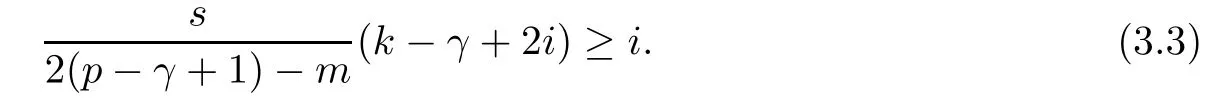
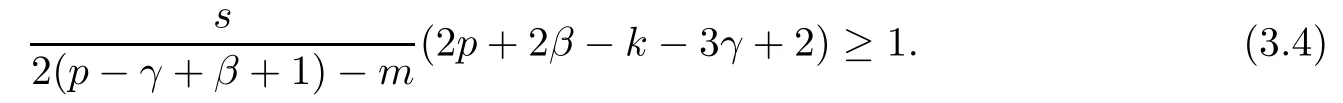
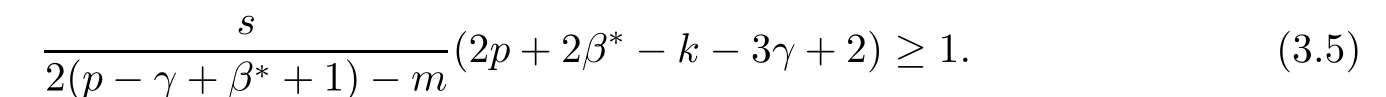
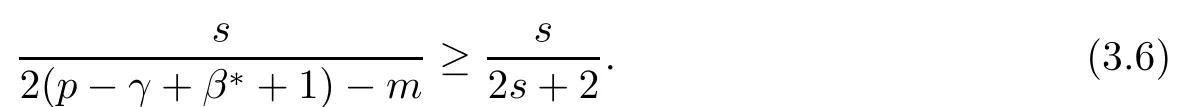

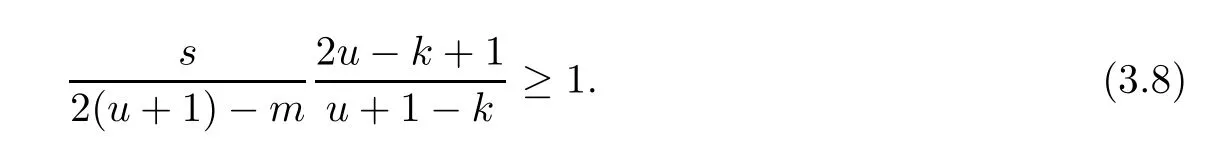


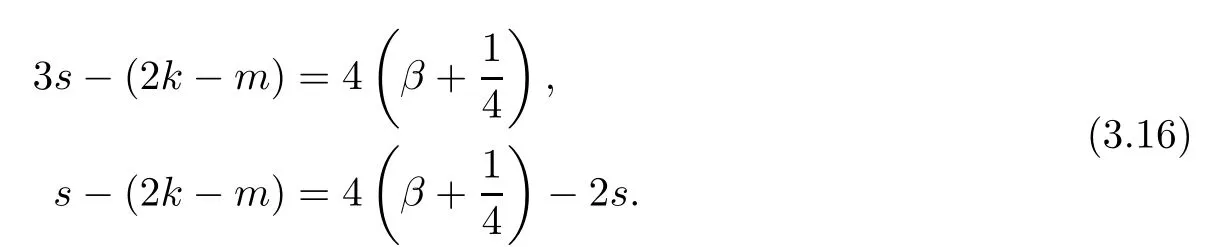



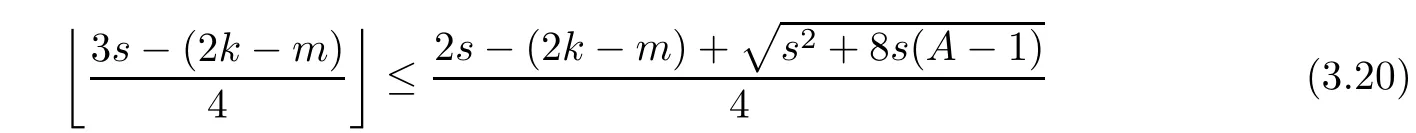
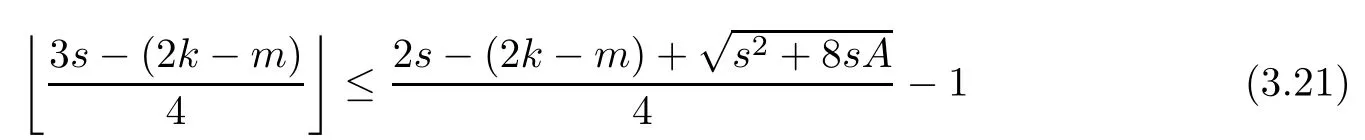
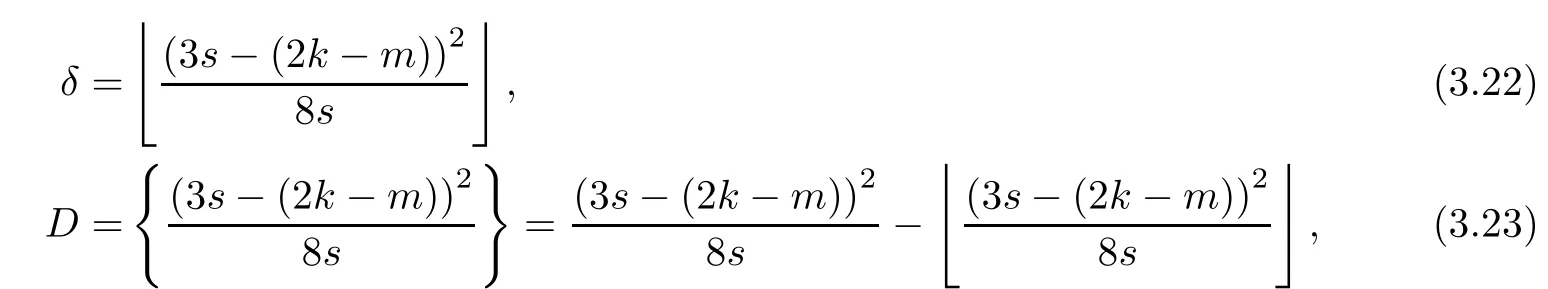
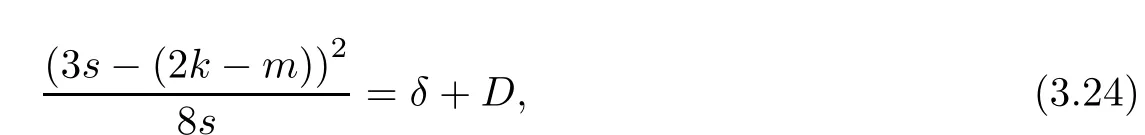



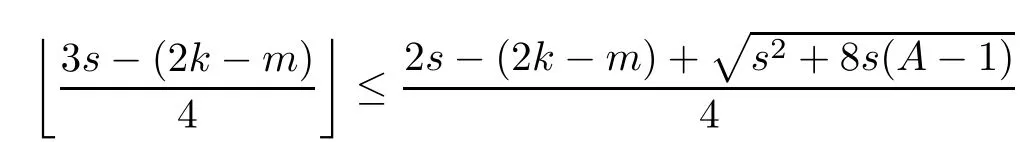
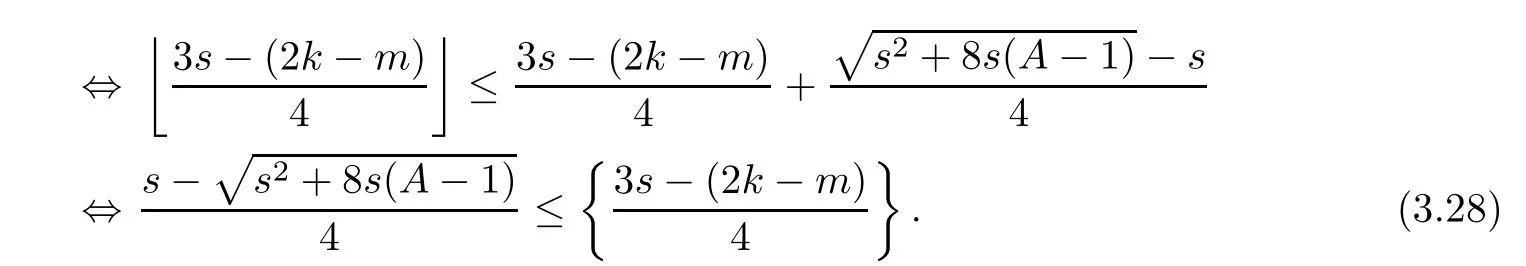
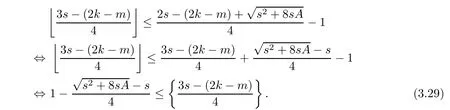

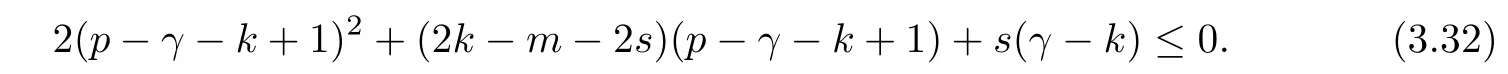
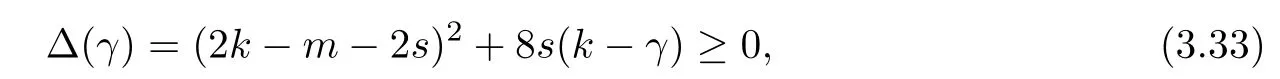
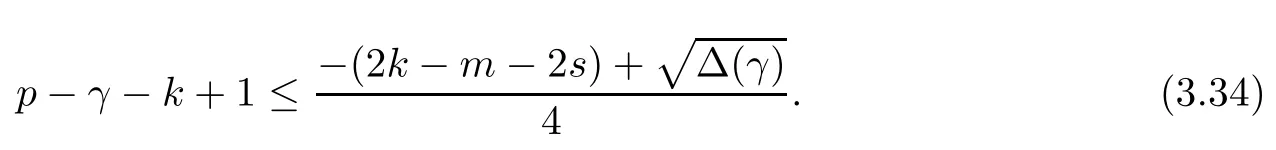
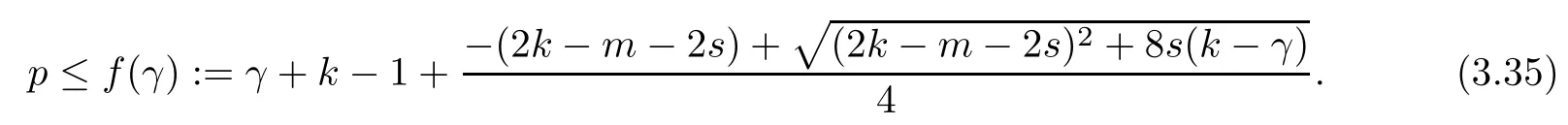
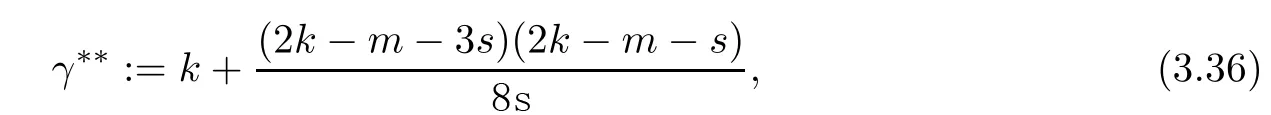
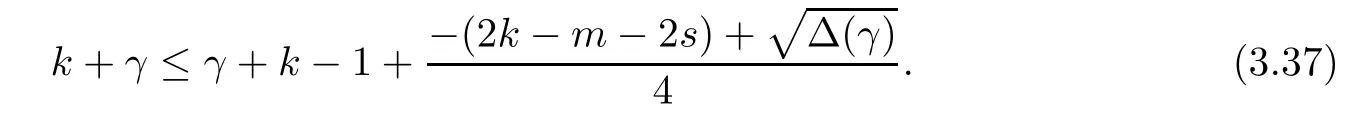
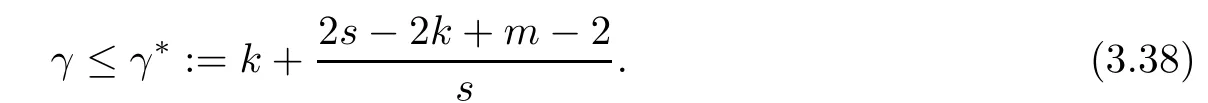
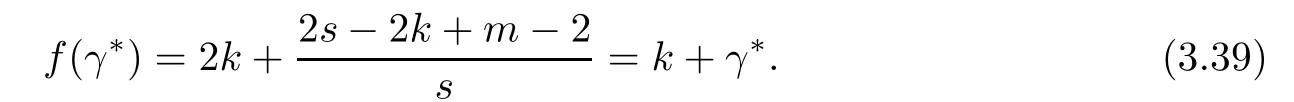



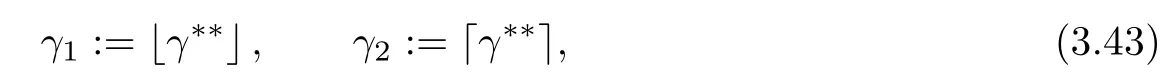
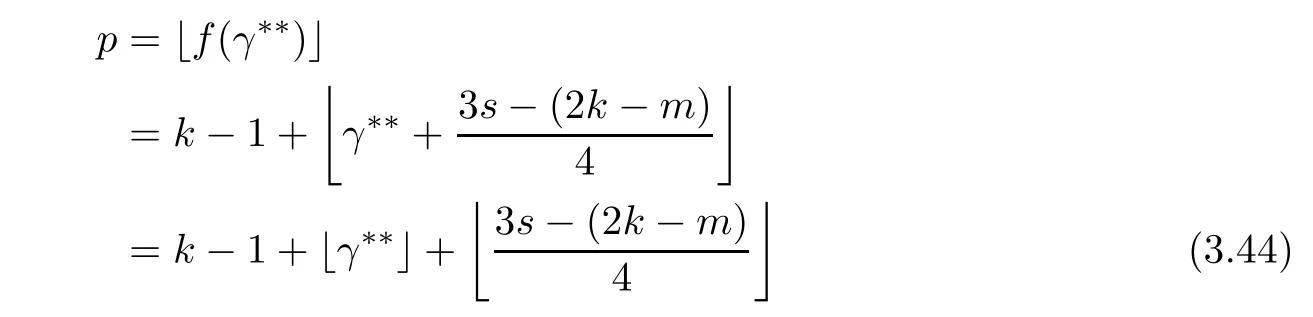
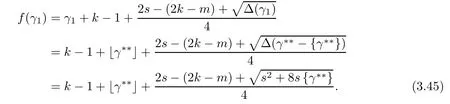
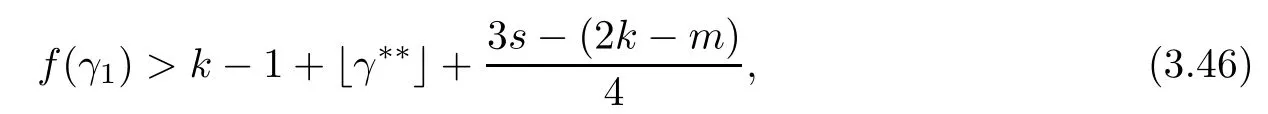

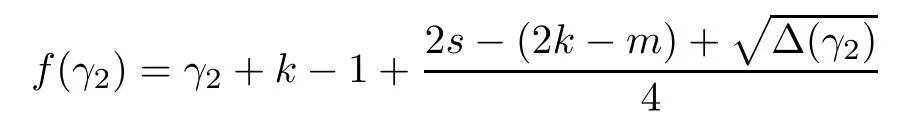
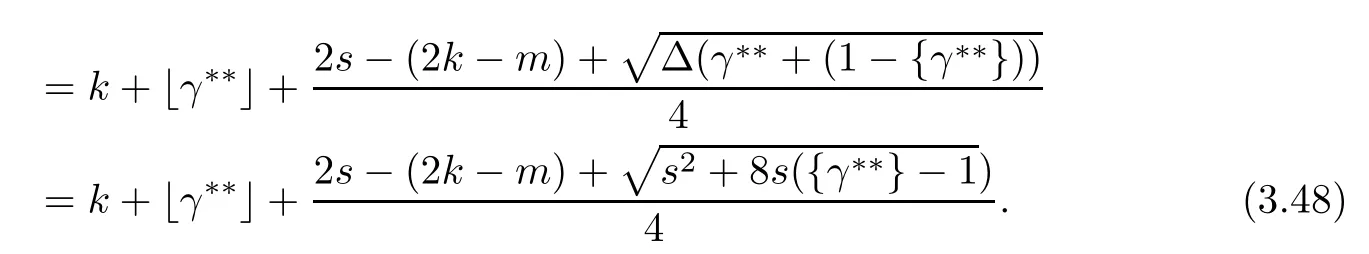
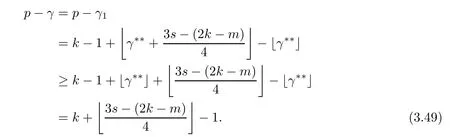



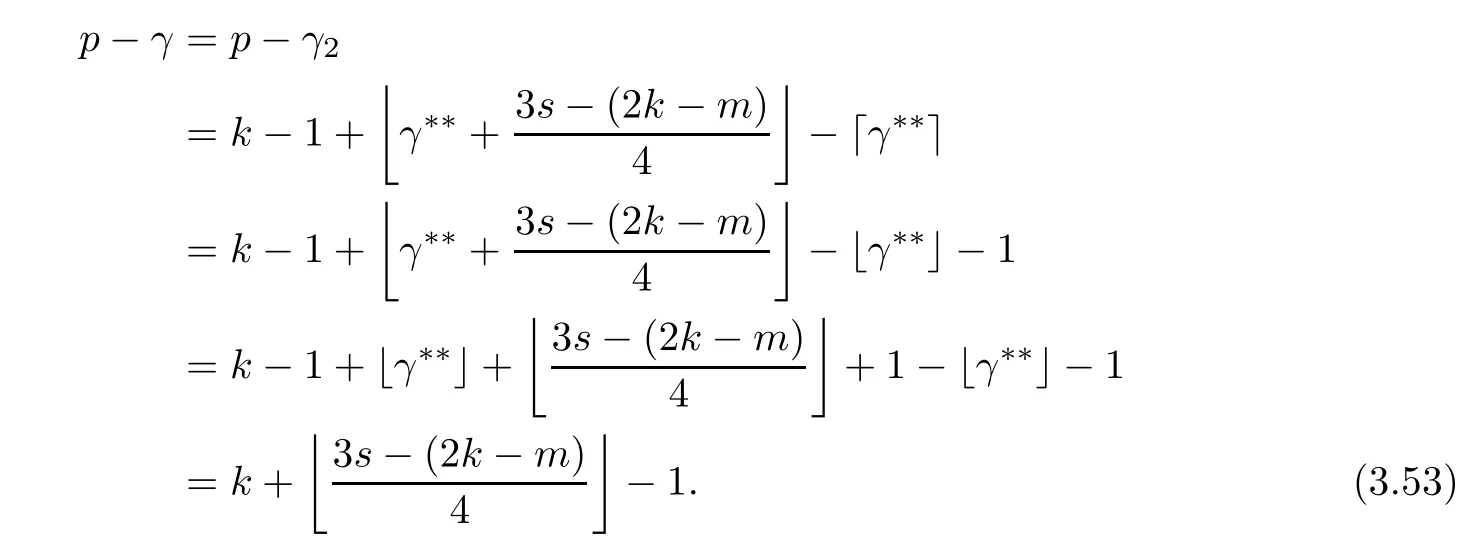

 Acta Mathematica Scientia(English Series)2020年1期
Acta Mathematica Scientia(English Series)2020年1期
