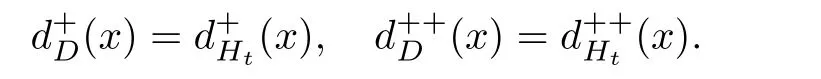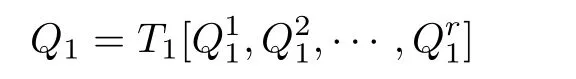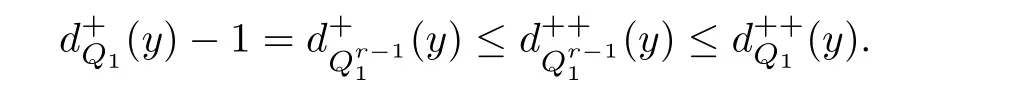準傳遞定向圖上的Seymour點
李瑞娟,史 杰,張新鴻
(1.山西大學數(shù)學科學學院,山西太原030006;2.太原科技大學應用數(shù)學系,山西太原030024)
§1 引 言
Seymour提出的關于定向圖的二次鄰域的問題是有向圖理論中最有趣,最具挑戰(zhàn)性的問題之一.這里,定向圖是指沒有2圈的有向圖.本文涉及到的有向圖是無環(huán),無平行邊的簡單有向圖,相關的術語和符號參看下一小節(jié)以及文獻[1].
猜想1.1[2](Seymour二次鄰域猜想) 在定向圖D中,總可以找到一個頂點x,這個頂點的二次外鄰域至少和它的外鄰域一樣大,即d+(x)6d++(x).
根據(jù)文獻[3],這樣的頂點x稱為Seymour點.
值得注意的是,猜想1.1只適用于定向圖,并不適用于一般的包含2圈的有向圖.例如,n個頂點的完全有向圖,對于每個頂點,都有即
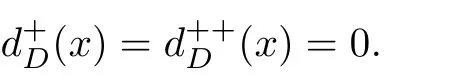
把Seymour二次鄰域猜想限制到競賽圖上,稱為Dean猜想.Fisher在文獻[4]中,利用Farkas引理,證明了Dean猜想[2],得到以下結論.
定理1.1[4]在任何一個競賽圖T中,都包含一個Seymour點.
Havet和Thomass在文獻[5]中給出了Dean猜想更基本的證明,并介紹了一種叫中間序的方法.他們的證明也得到了以下更強的結果.
定理1.2[5]若競賽圖T無出度為零的頂點,則T至少包含兩個Seymour點.
文獻[6]進一步發(fā)展了中間序的方法,證明了猜想1.1對于最小度為|V(D)|?2的有向圖D也同樣適用.同樣地,猜想1.1對于競賽圖減去一顆星,競賽圖去掉子競賽圖的弧集也同樣適用.Ghazal在文獻[7]中也使用了中間序的方法,證明了猜想1.1對于加權競賽圖去掉廣義星同樣適用.Kaneko和Locke在文獻[8]中證明了猜想1.1對于最小出度最多為6的定向圖也同樣適用.Cohn,Godbole,WrightHarkness和Zhang在文獻[3]中證明了該猜想對于某些隨機定向圖也適用.
證明猜想1.1的另一種方法是確定極大值γ,使得在每個有向圖D中存在一個頂點x滿足. 在猜想1.1中,γ=1.Chen,Shen和Yuster在文獻[9]中證明了γ≥r,其中r=0.657298···是2x3+x2?1=0的唯一實根.若對證明方法細化,他們還可以得到r≥0.67815···.近年來,二次鄰域問題被更多人研究,參看文獻[10-12].
本文將證明Seymour二次鄰域猜想在準傳遞定向圖上的正確性,通過研究準傳遞定向圖的Seymour點與擴張競賽圖的Seymour點之間的關系,得到:每個準傳遞定向圖至少包含一個Seymour點;無出度為零的點的準傳遞定向圖至少包含兩個Seymour點.
§2 術語,符號和基本結論
設D是一個有向圖,分別用V(D)和A(D)表示D的頂點集和弧集.
若有向圖D中的不同頂點u和v,存在從u到v的弧,則稱u控制v,寫成u→v,并稱v是u的外鄰點或者u是v的內鄰點.若對于D的一個子有向圖或僅僅是D的一個頂點子集H(可能有H=D),H中頂點u的外鄰點的集合用表示,稱它為H中頂點u的外鄰域.另外,稱為u在H中的出度.設
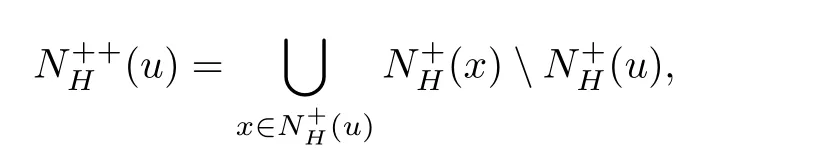
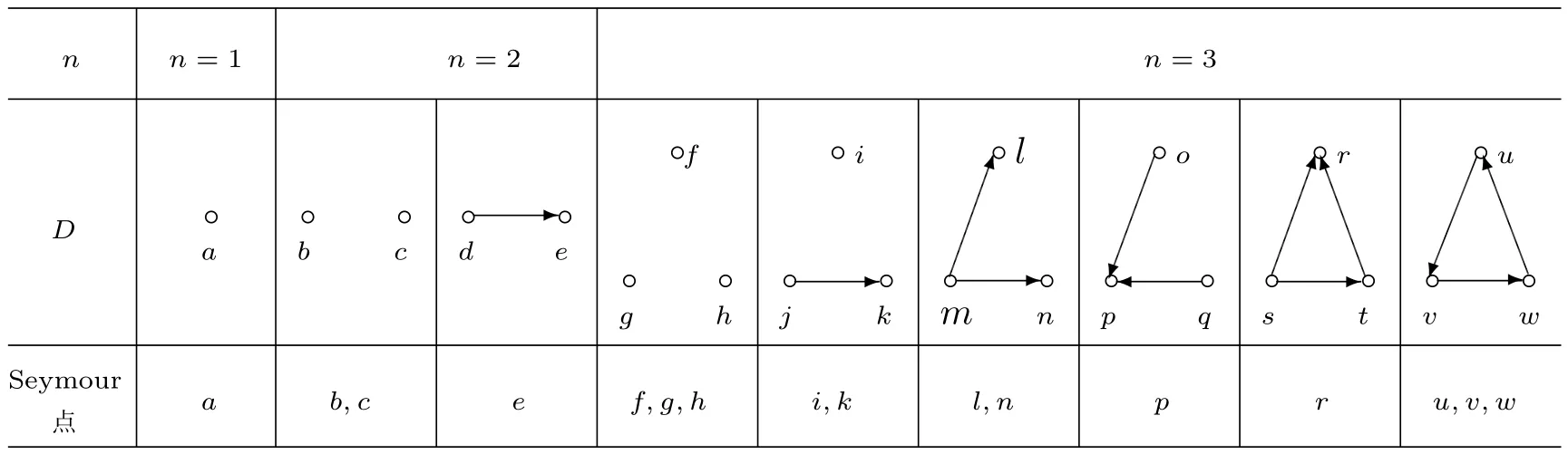
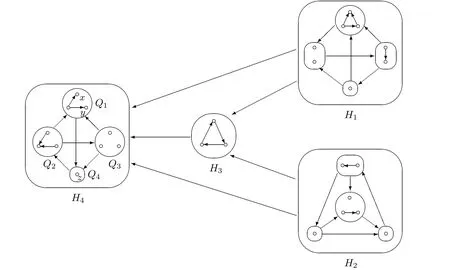
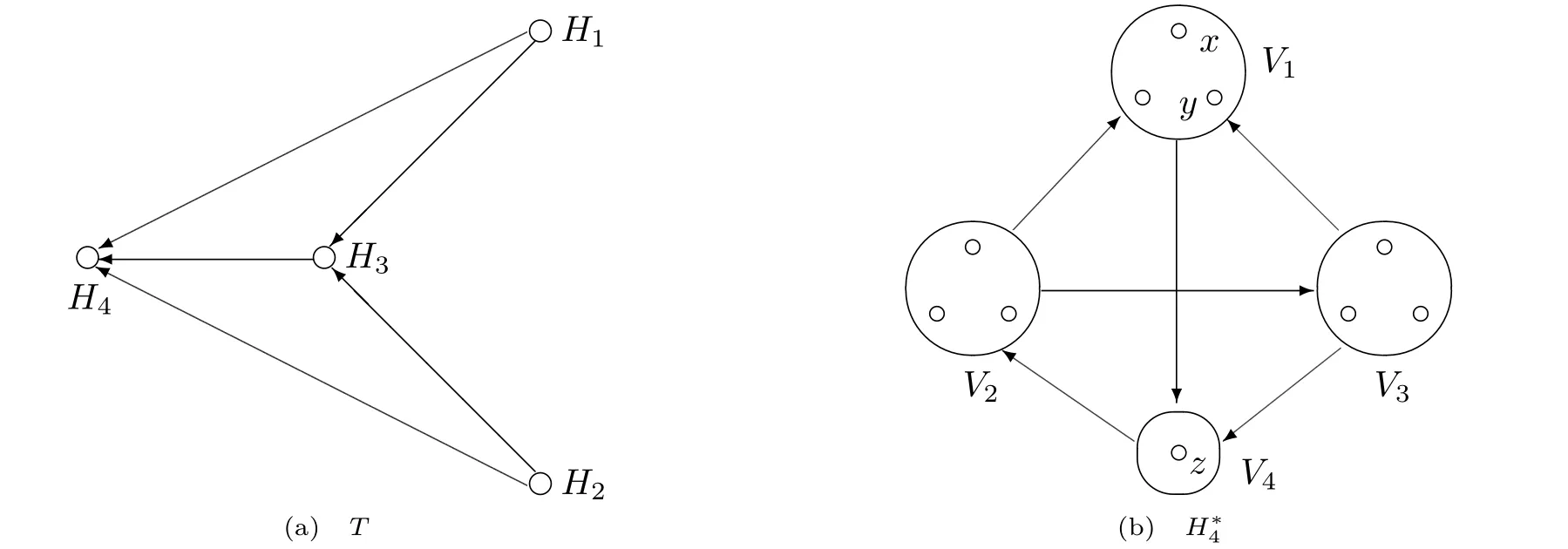
如果有向圖D沒有有向圈,那么它就是無圈的.如果對于無圈有向圖D的每一對弧xixj∈A(D),滿足i 若D=H[S1,S2,···,Sh],且每個有向圖S1,S2,···,Sh都沒有弧,則稱D是H的擴張.這時對每個i∈{1,2,···,h},Si稱為D的部集.若有向圖中每對不同的頂點都相鄰,則稱這個有向圖為半完全有向圖.沒有2圈的半完全有向圖稱為競賽圖.擴張競賽圖是指一個競賽圖的擴張.對于有向圖D中的三個不同的頂點x,y和z,若在D中存在弧xy,yz,在x和z之間總存在一條弧,那么稱有向圖D是準傳遞的.若在D中存在弧xy,yz,在x和z之間總存在弧xz,那么稱有向圖D是傳遞的.顯然每個傳遞有向圖是準傳遞的,每個擴張競賽圖也是準傳遞的. 為了簡化準傳遞有向圖上某些結論的證明,Bang-Jensen和Huang在文獻[13]中給出了這類有向圖的結構刻畫. 定理2.1[13]設D是一個準傳遞有向圖,則 (a)若D是非強連通的,則存在一個傳遞定向圖T,它的頂點集為{u1,u2,···,ut},還存在強連通的準傳遞有向圖H1,H2,···,Ht,使得D=T[H1,H2,···,Ht],其中對于任意的i∈{1,2,···,t},Hi代替了ui. (b)若D是強連通的,則存在一個強連通的半完全有向圖S,它的頂點集為{v1,v2,···,vs},還存在準傳遞有向圖Q1,Q2,···,Qs,使得Qi不是單點就是非強連通的,且D=S[Q1,Q2,···,Qs],其中對于任意的i∈{1,2,···,s},Qi代替了vi. 定理2.1中描述的分解稱為準傳遞有向圖D的典型分解. ' 圖1 一個非強連通的準傳遞定向圖D的典型分解 更多有關準傳遞定向圖的結論參看文獻[14-20]. 本文研究的是Seymour二次鄰域猜想對于準傳遞定向圖同樣適用,因為準傳遞定向圖是準傳遞有向圖沒有2圈時的特殊情況,所以在運用定理2.1時,需要取其沒有2圈的情況,也就是要把準傳遞有向圖用準傳遞定向圖代替.同樣地,半完全有向圖用競賽圖代替. 如圖所示,給出了一個非強連通準傳遞定向圖D的典型分解,這個典型分解可表示為D=T[H1,H2,H3,H4],其中,T為一個傳遞定向圖,如圖2(a)所示;對于任意的i∈{1,2,3,4},Hi是強連通的準傳遞定向圖.圖1中的大弧表示不同框集之間在顯示方向上有一個完全控制. 這部分考慮強連通準傳遞定向圖的Seymour點與擴張競賽圖的Seymour點之間的關系.為此,先考慮圖1的最后一個強分支H4,它是一個強連通的準傳遞定向圖,對于任意的i∈{1,2,···,s},用Qi的頂點集Vi代替Qi,得到一個擴張競賽圖,如圖2(b).容易驗證,V1和V4中的點都是中的Seymour點;x,y是Q1中的Seymour點;z是Q4中的Seymour點;x,y,z是H4中的Seymour點.由此可得,Q1和Q4中的Seymour點都是H4中的Seymour點. 圖2 傳遞定向圖T和擴張競賽圖 引理3.1設D是一個強連通的準傳遞定向圖,它的典型分解為D=S[Q1,Q2,···,Qs].設D?=S[V1,V2,···,Vs]是一個擴張競賽圖,其中,對于任意的i∈{1,2,···,s},Vi是子有向圖Qi的頂點集.若存在一個頂點v∈Vi,使得v是Qi的一個Seymour點,同時也是D?的一個Seymour點,那么v也是D的一個Seymour點. 證因為v是Qi中的一個Seymour點,也是D?中的一個Seymour點,則有 由于D?是擴張競賽圖,顯然有 這部分考慮擴張競賽圖上的Seymour點.首先證明猜想1.1對擴張競賽圖是成立的. 定理4.1每個擴張競賽圖至少包含一個Seymour點. 證設D=S[V1,V2,···,Vs]是一個擴張競賽圖,其中每個Vi都是一個獨立集.現(xiàn)用一個和Vi有相同頂點集的傳遞競賽圖代替每個Vi,這樣就得到了一個新的有向圖D0.顯然,D0是一個競賽圖,由定理1.1得,D0存在一個Seymour點,設為x,即有又有 此外,定理1.2也可以推廣到擴張競賽圖中.事實上,可以得到更強的結論,即如果這兩個Seymour點在同一部集中,則至少有一個點的二次外鄰域的頂點個數(shù)嚴格大于一次外鄰域的頂點個數(shù). 定理4.2設D=S[V1,V2,···,Vs]是一個擴張競賽圖,且每個Vi是獨立集.若D中無出度為零的頂點,則 (a)D中至少包含兩個Seymour點; (b)D中至少存在一個Seymour點x,使得,除非存在另一個和x在不同部集的Seymour點y. 證設D=S[V1,V2,···,Vs]是一個擴張競賽圖.現(xiàn)用一個和Vi有相同頂點集的傳遞競賽圖代替每個Vi,這樣D就變成了一個新的競賽圖T.因為D無出度為零的頂點,所以T的每個頂點出度也不為零.根據(jù)定理1.2,T中至少包含兩個Seymour點x,y,則顯然 則x,y也是D上的Seymour點,故(a)成立. 若這兩個Seymour點x,y在不同的部集中,則(b)成立.故假設這兩個Seymour點x,y在相同的部集中,即有某個i∈{1,2,···,s},x,y∈Vi.不失一般性,假設在T中x控制y.因此 由此可得(b)成立. 這部分考慮準傳遞定向圖上的Seymour點.設D是一個準傳遞定向圖,它的階數(shù)為n.表1列出了當n=1,2,3時所有的準傳遞定向圖,并在表1的第三行中指出對應圖的Seymour點. 表1 n=1,2,3時所有的準傳遞定向圖及其Seymour點 下面證明猜想1.1對準傳遞定向圖是成立的. 定理5.1每個準傳遞定向圖至少包含一個Seymour點. 證設D是一個準傳遞定向圖,通過對D的階數(shù)n進行歸納證明.參看表1,易知當1≤n≤3時,結論成立.現(xiàn)假設n≥4. 情形1D是非強連通的. 設D=T[H1,H2,...,Ht]是D的典型分解,其中,T是傳遞定向圖,且對i∈{1,2,···,t},Hi是強連通的準傳遞定向圖.不失一般性,現(xiàn)假設H1,H2,···,Ht是D的強分支無圈序.通過歸納假設,設x是Ht的Seymour點,則.顯然 情形2D是強連通的. 設D=S[Q1,Q2,···,Qs]是D的典型分解,其中,S是強連通的競賽圖,且對i∈{1,2,···,s},Qi是單點或者非強連通的準傳遞定向圖.設D?=S[V1,V2,···,Vs]是一個擴張競賽圖,其中,對i∈{1,2,···,s},Vi都是子有向圖Qi的頂點集.由定理4.1可知,D?有一個Seymour點x.現(xiàn)假設x∈Vi,則Vi的每個頂點都是D?中的Seymour點.由歸納假設,Qi有一個Seymour點,也記為x.則由引理3.1可知,x也是準傳遞定向圖D中的一個Seymour點. 根據(jù)定理5.1的證明,在圖1所示的準傳遞定向圖D中,最后一個強分支H4中的Seymour點就是D中的Seymour點.通過觀察,頂點x,y,z是H4中的Seymour點,也是D中的Seymour點.又注意到,在圖1所示的準傳遞定向圖D中,每個頂點的出度都不為零,且D包含的 Seymour點多于1個.現(xiàn)證明,定理1.2可以推廣到準傳遞定向圖中. 定理5.2設D是準傳遞定向圖,若D中無出度為零的頂點,則D中至少包含兩個Seymour點. 證現(xiàn)通過對D的階數(shù)n進行歸納證明.顯然n≥3.參看表1,易知當n=3時,結論成立.現(xiàn)假設n≥4. 情形1D是非強連通的. 設D=T[H1,H2,···,Ht]是D的典型分解,其中,T是傳遞定向圖,且對i∈{1,2,···,t},Hi是強連通的準傳遞定向圖.不失一般性,假定H1,H2,···,Ht是D的強分支無圈序.因為D無出度為零的頂點,所以最后一個分支Ht至少包含3個頂點,即Ht是一個每個頂點出度都不為零的準傳遞定向圖.通過歸納假設,在Ht中至少包含兩個Seymour點.因為Ht中的每一個Seymour點也是D的Seymour點,所以D中至少包含兩個Seymour點. 情形2D是強連通的. 設D=S[Q1,Q2,···,Qs]是D的典型分解,其中,S是強連通競賽圖,且對i∈{1,2,···,s},Qi是單點或者非強連通的準傳遞定向圖.設D?=S[V1,V2,···,Vs]是一個擴張競賽圖,這里對i∈{1,2,···,s},Vi是子有向圖Qi的頂點集.顯然D?是強連通的且無出度為零的頂點.由定理4.2(b)可得,要么存在一個Seymour點x,使得;要么存在另一個和x在不同部集的Seymour點y.在后面這種情況下,D?有兩個屬于不同部集的Seymour點,記這兩個部集為Vα和Vβ.由歸納假設,對每個i∈{1,2,···,s},Qi都至少包含一個Seymour點.特別地,Qα和Qβ中都包含Seymour點.再由引理3.1可知,Qα和Qβ中的Seymour點也是D的Seymour點.因此在這種情形下D包含兩個Seymour點. 現(xiàn)考慮前面一種情形,即D?中存在一個Seymour點x,使得為了方便,設x∈V1.如上所述,Q1中的Seymour點,仍記為x,也是D的Seymour點.下面尋找D的另一個Seymour點. 首先斷言部集V1中至少包含2個頂點.否則,x是V1中的唯一頂點.由定理4.2(a)知,D?中存在另一個不在V1的Seymour點y.如上所述,y所在的部集中必存在D的另一個Seymour點.結論成立.故假設V1至少包含2個頂點. 如果Q1至少包含兩個Seymour點,則它們也是D中的Seymour點.故假設Q1恰好只有一個Seymour點x. 現(xiàn)斷言V1中存在一個不同于x的頂點y,使得.設 是Q1的典型分解,其中,T1是一個傳遞定向圖,且對是強連通的準傳遞定向圖.類似地,假定是Q1的強分支無圈序.易知,是唯一的終止強分支,且x是中唯一的頂點.否則,Q1中會有除x外的其它Seymour點,與假設矛盾.由歸納假設,在中存在一個Seymour點y,則.現(xiàn)有 從而斷言成立. 因為y和x在D?的相同部集V1中,所以它們的外鄰域和二次外鄰域在D?中是相同的,從而不等式也成立.顯然 綜上所述,該定理成立.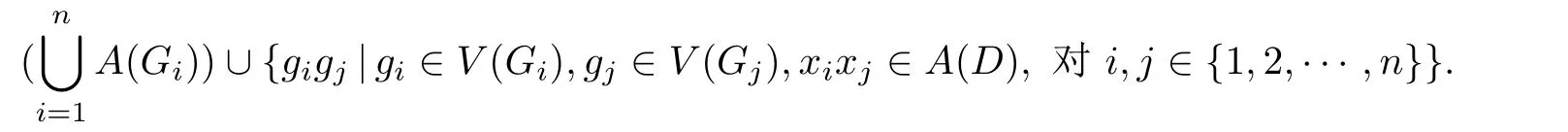
§3 準傳遞定向圖和擴張競賽圖的Seymour點的關系
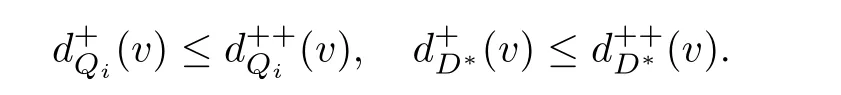
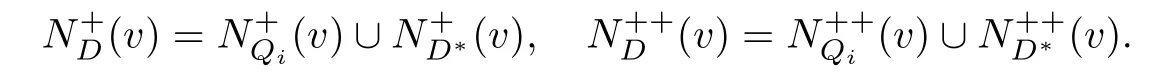
§4 擴張競賽圖的Seymour點
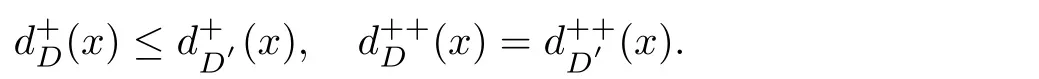
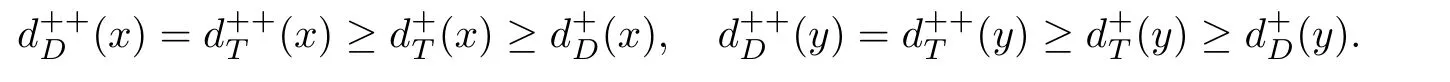
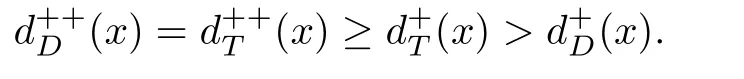
§5 準傳遞定向圖的Seymour點