Shivarudhrappa Raghu, Natarajan Sriraam, Yasin Temel, Shyam Vasudeva Rao, Alangar Sathyaranjan Hegde, Pieter L Kubben

1Department of Neurosurgery, School for Mental Health and Neuroscience of the Faculty of Health, Medicine and Life Sciences, Maastricht University, Maastricht 6200 MD, the Netherlands;2Center for Medical Electronics and Computing, M.S. Ramaiah Institute of Technology, Bengaluru, Karnataka 560054,India;3Department of Neurosurgery, Maastricht University Medical Center, 4Department of Neurosurgery, Maastricht University, Maastricht 6200 MD, the Netherlands;5Institute of Neuroscience, Ramaiah Medical College and Hospitals, Bengaluru, Karnataka 560054, India.

Abstract In this paper, complexity analysis and dynamic characteristics of electroencephalogram (EEG) signal based on maximal overlap discrete wavelet transform (MODWT) has been exploited for the identification of seizure onset.Since wavelet-based studies were well suited for classification of normal and epileptic seizure EEG, we have applied MODWT which is an improved version of discrete wavelet transform (DWT). The selection of optimal wavelet sub-band and features plays a crucial role to understand the brain dynamics in epileptic patients.Therefore, we have investigated MODWT using four different wavelets, namely Haar, Coif4, Dmey, and Sym4 sub-bands until seven levels. Further, we have explored the potentials of six entropies, namely sigmoid, Shannon,wavelet, Renyi, Tsallis, and Steins unbiased risk estimator (SURE) entropies in each sub-band. The sigmoid entropy extracted from Haar wavelet in sub-band D4 showed the highest accuracy of 98.44% using support vector machine classifier for the EEG collected from Ramaiah Medical College and Hospitals (RMCH). Further, the highest accuracy of 100% and 94.51% was achieved for the University of Bonn (UBonn) and CHB-MIT databases respectively. The findings of the study showed that Haar and Dmey wavelets were found to be computationally economical and expensive respectively. Besides, in terms of dynamic characteristics, MODWT results revealed that the highest energy present in sub-bands D2, D3, and D4 and entropies in those respective sub-bands outperformed other entropies in terms of classification results for RMCH database. Similarly, using all the entropies, sub-bands D5 and D6 outperformed other sub-bands for UBonn and CHB-MIT databases respectively. In conclusion, the comparison results of MODWT outperformed DWT.

Keywords: electroencephalogram, epileptic seizures, entropy, maximal overlap discrete wavelet transform,sigmoid entropy, support vector machine

Introduction

Epilepsy is a neurological disorder that causes an uncontrolled and involuntary movement characterized by unprovoked seizures[1]. A seizure occurs when a burst of electrical impulses in the brain escapes their normal limits[2]. Epilepsy is the fourth most common neurological disease and 2.2 million people or 7.1 in every 1 000 people of the world suffer from it[2–3].Depending on where the seizure starts, they are portrayed as being focal onset, generalized onset or unknown onset. Electroencephalogram (EEG)contains abundant information on neural,physiological and pathological conditions of brain disorders. It is essential to identify the distinctive parameter that is capable of revealing the dynamic characteristics of the brain in epileptic patients.However, manual inspection of immense EEG data recorded over a long time found to be a timeconsuming and tiresome task by experts in hospitals.Further, the manual inspection between different experts may produce odd results that tend to wrong classification. Therefore, it is essential to develop an automated model with the optimal selection of features and classifiers. To address the abovementioned limitations, we propose the automated seizure onset detection model using maximal overlap discrete wavelet transform (MODWT) based entropies and support vector machine (SVM) classifier. Hence,timely detection and diagnosis of epileptic patients gain prioritized clinical attention around the world.

In recent years, extensive research on epileptic seizures has been done using discrete wavelet transform (DWT). Wavelet-based methods were found to be outperformed in terms of time-frequency resolution, denoising, different temporal scales and robustness to outliers[4]. DWT with the statistical features[5–7], signal energy[8], eigenvalues[9], and 21 different features[10]have been reported promising results. Normal, pre-ictal and ictal EEGs were studied using wavelet packet transform with log and norm entropies[11]. Complexity analysis of EEG was explored in different sub-bands of DWT using approximate entropy[12]. DWT and SVM based algorithm showed better results for long-term EEGs[13]. In our recent study[14], 100% accuracy was reported using minimum variance modified fuzzy entropy in 38 patients. Further, approximate entropy,Phase entropy 1 and 2, and sample entropy[15],weighted permutation entropy[16], Renyi, spectral and Shannon entropies[17–19]and wavelet entropy[20]have been explored for epileptic seizure studies. Acharyaet alhave reviewed the application of different entropies for seizure detection and reported advantages and shortcomings[21].

Spike-wave-discharge onset was identified using MODWT coefficients for absence seizure detection[22].MODWT and log-normal distribution based model was evaluated using random forest classifier[23]. In this study, the authors did not analyze the energy distribution and different wavelets were not varied.Epileptic seizure prediction was performed using MODWT and nonlinear similarity index[24]. This study showed the best performance in the beta (10–30 Hz)frequency band. An extensive analysis between MODWT and DWT for functional brain network construction demonstrated the optimal ways of choosing the wavelet method, filters, and decomposition level[4]. The results suggested that MODWT outperformed DWT and produced fewer variable estimates than DWT. MODWT correlation coefficients measure exhibited good spatial correspondence between intracranial and scalp EEG[25]. MODWT sub-bands have yielded an accuracy of 99.26% using feed-forward artificial neural networks[26].

The literature survey suggests that most of the studies[11,15,17,23,27]have conducted on one of the oldest publicly available University of Bonn EEG databases[28]. Further, very few studies have investigated MODWT on EEG signals and studied the effect of entropy index of Renyi, Tsallis and SURE entropies. In addition, the dynamic characteristics of EEG have not been studied for different sub-bands and entropies for epileptic EEG. MODWT is the modified version of DWT without down-sampling in each decomposition level and it is a highly redundant,and nonorthogonal transform[29–30]. Elimination of down-sampling in MODWT avoids the loss of information and enhances the time-frequency resolution on each scale. Therefore, in our study,MODWT was selected for EEG decomposition with Haar, Coif4, Dmey, and Sym4 wavelets. The measure of entropy used to quantify the uncertainty of the signal either in the time or frequency domain. To reveal the dynamic characteristics and complexity analysis of EEG signal sigmoid, Shannon, Wavelet,Renyi, Tsallis, and Steins unbiased risk estimator(SURE) entropies were implemented in our study.Hence, the goal of the study was to identify the computationally efficient optimal combination of MODWT sub-band with entropies using the SVM classifier for the detection of seizure onset.

Fig. 1depicts the flow of the proposed epileptic seizure detection algorithm. The proposed method has been divided into five stages. Stage 1: Recordings of EEG at the hospital. Stage 2: The raw EEG signals were pre-processed to eliminate line noise and artifacts. Stage 3: The EEG signals were decomposed using MODWT with four different wavelets. Stage 4:Six entropies were extracted from each sub-band.Stage 5: Finally, the entropies were classified using SVM classifier.

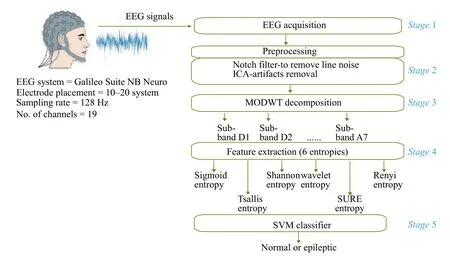
Fig. 1 Block diagram of the proposed algorithm.

The rest of the paper has been organized as follows.In Section 2, a brief introduction of EEG data, preprocessing, MODWT and feature extraction methods were described. The experimental results are presented in Section 3 followed by a discussion in Section 4. Finally, Section 5 concludes the importance of the proposed study.

Materials and methods

EEG recordings

The proposed algorithm was validated on three databases, namely Ramaiah Memorial College and Hospitals (RMCH), University of Bonn (UBonn), and Boston Children's Hospital-Massachusetts Institute of Technology (CHB-MIT) EEG recordings.

The EEG recordings used in our study were obtained from the RMCH, Bengaluru, India after ethical clearance was obtained to use the EEG for research purposes[14]. This unipolar EEG was recorded using 19 scalp electrodes (Fp1, Fp2, F7, F3, Fz, F4,F8, T3, C3, Cz, C4, T4, T5, P3, Pz, P4, T6, O1, and O2) placed according to the International 10–20 system configuration at a sampling rate of 128 Hz using Galileo Suite NB Neuro digital EEG system.The complete database comprises of 115 subjects (67 males and 48 females) ranging between 2.5 to 75 years of age with the average age of (40.0±20.3)years. Two experts at RMCH visually marked EEG as normal and epileptic segments. A total of 162 seizures were found from approximately 58 hours of EEG,which was collected from 115 subjects. In total,RMCH database consists of approximately 4.36 hours of epileptic seizures data and approximately 53 hours of normal EEG. The length of the recording duration of each patient varied from 20 minutes to 3 hours.

The second database used in our research was collected from publicly available EEG recordings from the UBonn (http://epileptologie-bonn.de/cms/fron t_content.php?idcat=193&lang=3&changelang=3)[28].These recordings were recorded from five different subjects undergoing presurgical evaluations. UBonn recordings were converted from multi-channel to single channel EEG by original researcher[5]. UBonn EEG was divided into five sets (A–E), each set consisting of 100 single channel EEG segments of 23.6 seconds duration recorded at a sampling rate of 173.61 Hz. Each subset corresponded to normal with the eye open (set A), normal with eye closed (set B), pre-ictal(set C), post-ictal (set D) and ictal state (set E). In our present study, four classification problems, namely{A}-{E}, {ACD}-{E}, {ABCD}-{E}, and {AB}-{CD}-{E} between epileptic and non-epileptic groups were considered based on the previous studies[3,15,30,31].

The last and third EEG database was collected from CHB-MIT[32]open-source available in Physionet repository (http://www.physionet.org/pn6/chbmit). It is one of the largest databases consisting of 844 hours of EEG recordings with 182 seizures from 23 patients.This EEG was recorded using the 10–20 international system bipolar montage electrode placement with 23 channels at a sampling rate of 256 Hz. For more details on the EEG database and patient information[32–33].

Preprocessing

The patients' EEG collected from RMCH database was preprocessed using suitable signal processing techniques. A 50 Hz notch filter was implemented to eliminate power line interference. Further, EEG was filtered using a bandpass filter between 0.5 Hz to 40 Hz. To eliminate the artifacts (eye blink, muscle artifacts, and electrode displacement) from EEG,independent component analysis was applied[34].

Maximal overlap discrete wavelet transform (MODWT)

The MODWT is an improved version of DWT[29–30].The MODWT is a linear filtering method that decomposes the signal into coefficients over a set of scales. The MODWT differs from DWT in terms of flexible time-frequency representation, highly redundant, non-orthogonal, and eliminates downsampling at each level of decomposition[23]. Further,MODWT is well-defined for all sample sizes N ,whereas DWT requires N to be a multiple of 2JforJlevels.

The input data are samples of a functionf(x)evaluated at N many time points. The function can be expressed as a linear combination of the scaling function ? (x) and wavelet ψ (x) at varying scales and translations[29–30]:

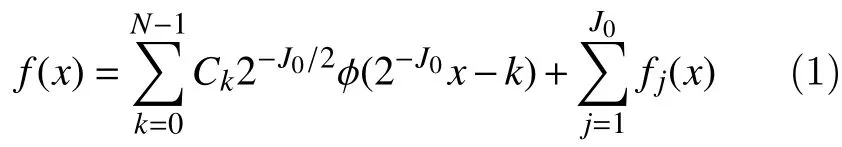
The MODWT partitions the energy across the various scales and scaling coefficients are as follows[29–30]:

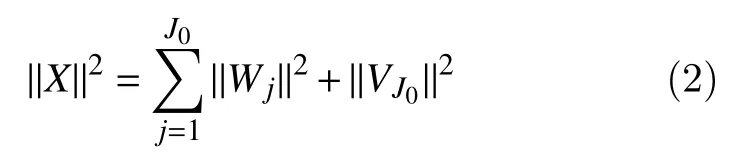
whereXis the input data,Wjare the detail coefficients at scalej, andVJ0are the final-level scaling coefficients.

The selection of wavelet function and decomposition level plays a significant role in analyzing EEG signals using MODWT that depends on the dominant frequency distribution in each subband. EEG was decomposed till level 6 using Haar wavelet, but other wavelets were not investigated[23,35].Therefore, in this study, four different mother wavelets, namely Haar, Coif4, Dmey, and Sym3 have been used to decompose EEG till level 7 (RMCH and UBonn) and level 10 (CHB-MIT) to identify the optimal combination for seizure onset detection.

Feature extraction

The entropy of EEG reflects the amount of uncertainty or randomness the signal[16]. The measure of entropy used to quantify the uncertainty of the signal either in the time or frequency domain. To reveal the dynamic characteristics and complexity analysis of the EEG signal, the following six entropies were investigated in our study. Most studies have reported the results using a single entropy index for Renyi, Tsallis, and SURE entropies. Whereas, in our study, these entropies were varied with different entropy index. The segmentation length of 1 second was used to extract the features.

Sigmoid entropy

In our recent study, sigmoid entropy has been proposed for the identification of seizure onset[36]. As we know that, a sigmoid function is a particular case of the logistic function having "S" shaped curve. EEG contains nonlinear elements which indicate the neuronal activity of epileptiform discharges. The sigmoid function is non-linear activation function the output always bounded to be in range (0,1). Since EEG is a non-linear signal, we are introducing sigmoid entropy by bringing the concept of probabilities to the sigmoid function.

As we know that sigmoid function is defined as[37]:

In our study, assuming thatnis the number of possible states that the amplitude of the EEG are quantized into andpithe probability of each state isThe probability of occurrence of EEG signal is calculated using histogram method by specifying bin ranges (0.05 microvolts based on the preliminary study).

Now by replacingtwithpin equation (3), wherep={p1,p2,p3,..,pn}, equation (3) becomes:

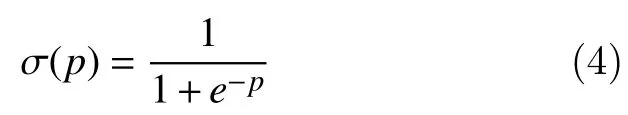
Expanding equation (4), we obtain:

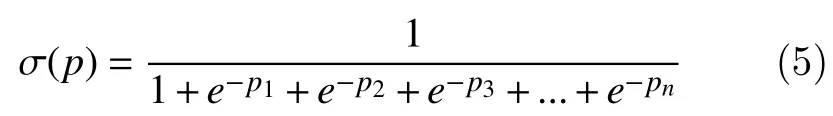
The amount of sigmoid entropy (HSigmoidEn)captured by equation (5) can be written as[36]:

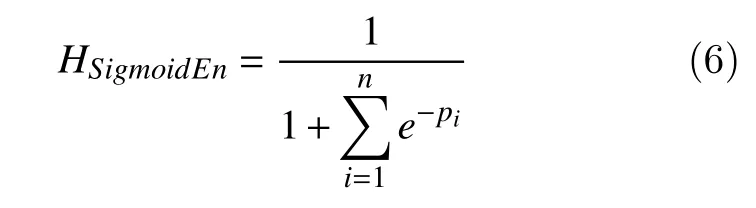
The dynamic range of the sigmoid entropy lies between 0 and 1. According to the characteristics of the sigmoid function, maximum entropy of '1' would infer the less variation of the signal[36]. In contrast,more variation or fluctuation of the signal may indicated by low entropy.

Shannon entropy

Shannon entropy is most widely used probability based entropy for EEG signals[38]and it is given by:

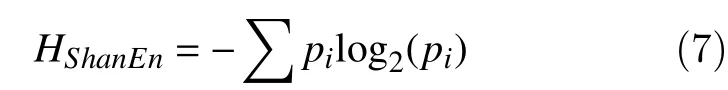
Wherepiis the probabilities of occurrence of possible states in decomposed EEG signals.Wavelet entropy

Wavelet entropy is a non-normalized Shannon entropy estimated from wavelet coefficients and it is given by[38–39]:

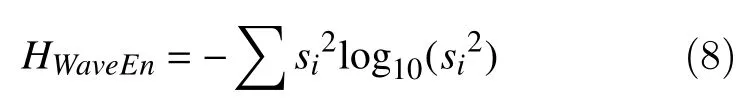
Renyi entropy

Renyi entropy is a generalization of Shannon entropy, which quantifies diversity, uncertainty or randomness of a system. It includes other entropy measures as special cases.

Renyi entropy of order α is defined as[40]:

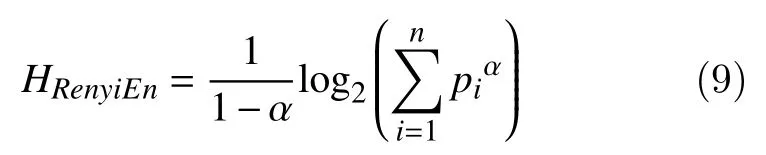
Wherepiis the probabilities of decomposed EEG signals, α is the order or entropy index ( α ?0), in our study α =2,3, and 5 was chosen.

Tsallis entropy

Tsallis entropy is a non-extensive generalization of Boltzmann-Gibbs entropy[41]. For a set of probabilities{pi}, Tsallis entropy is defined as:

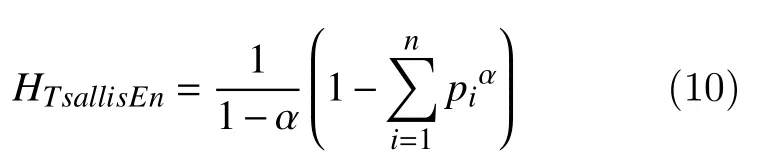
where α is the entropy index which is positive parameter. In our study α was chosen to be 1.5, 3 and 5.SURE entropy

SURE entropy is measuring tool for quantifying properties related to information for an accurate representation of a signal and it defined as[42]:

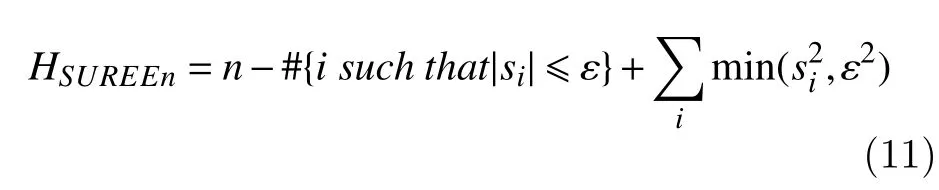
where,siis the decomposed EEG signal and ε is a positive threshold value or entropy index. In our study, ε was varied as 1, 3, and 5.

Classification

The classification of epileptic seizures was performed using the SVM classifier due to its better performance in previous studies[5,7,12–13,43–45]. SVM used kernel method to transform the feature set that drew an optimal boundary between the possible outputs[12]. The preliminary study revealed the better performance using radial basis function kernel as compared to other kernel functions and the same was implemented for further analysis. SVM classifier was implemented using leave-one-out-subject crossvalidation to achieve the robustness of the method.Further tuning parameters were set as follows: Kernel function=radial basis function, Kernel Scale=auto,Box Constraint=1, and Standardize=true. The performance of the proposed seizure detection technique was evaluated using sensitivity, specificity,and accuracy.

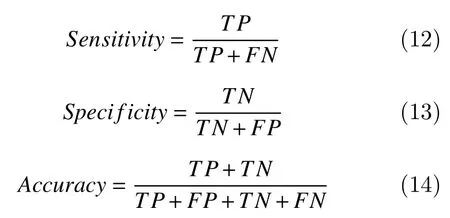
Where,TPis true positive,FNis false negative,TNis true negative andFPis false positive.

Results

In this section, we have investigated the effects of different wavelet methods and decomposition length on (i) energy content in each sub-band of EEG (ii)variation of entropy in each sub-band distinguishing between normal and epileptic EEG (iii) classification results.Fig. 2shows the example of epileptic EEG collected from RMCH database with seizure onset and offset. As discussed in the previous section, we have applied seven level MODWT on EEG signals configured using Haar, Coif4, Dmey, and Sym4 wavelets. Basically, these results help to understand the EEG brain dynamics in terms of energy distribution, the behavior of entropy and classification results in each sub-band. The EEG signal and its coefficients corresponding to each sub-band using Haar wavelet were depicted inFig. 3. It is clear that the length of the decomposed signal in each level is the same as the original EEG. Further, energy and entropies were estimated in each sub-band.

Effect of decomposition level on energy

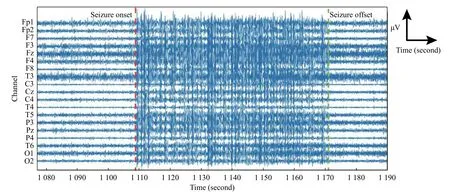
Fig. 2 An example of epileptic seizure EEG from RMCH database. The red marker indicates the beginning of the seizure onset and green marker its end.

Fig. 4demonstrates the distribution of energy in each sub-band decomposed using MODWT configured with Haar, Coif4, Dmey, and Sym4 wavelets. We have investigated the energy distribution in every sub-band for annotated normal and epileptic EEG using different mother wavelet functions. We observedP<0.01 in all the sub-bands except for subband A7 in level 7. We found that energy content in the levels 2 (sub-band D2), 3 (sub-band D3), and 4(sub-band D4) was significantly high as compared to the other levels for all the wavelets. In all the wavelets, least energy was found to be in sub-band A7. In addition, the range of distribution was very less in sub-bands D2, D3, and D4. It shows that the level of decomposition has an effect on the amount of information revealed in EEG signals.

Effect of MODWT decomposition length entropies

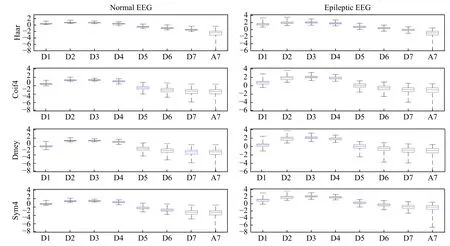
Fig. 4 Boxplot describing distribution of energy in MODWT EEG over different scales.

In this section, we have demonstrated the behavior of entropies when decomposed using MODWT.Fig. 5shows the effect of MODWT decomposition length on entropies for different decomposition levels and wavelets. InFig. 5A, sigmoid entropy exhibited lower for epileptic and higher for normal EEG. We observed that sigmoid entropy increased as the function of decomposition length and lies between 0 to 1. In contrast to sigmoid entropy, Shannon entropy and wavelet entropies behaved quite different. That means,higher and lower entropies were obtained for epileptic and normal EEG respectively.

Fig. 5Bdepicts the entropies obtained for Renyi entropy (α = 2, 3, and 5). Renyi entropy was found to be increasing as entropy index α goes higher. Similar observation was seen for SURE entropies for ε = 1, 3,and 5 (Fig. 5D). Tsallis entropy was seen to be decreasing as the entropy index α = 1.5, 3, and 5 increases (Fig. 5C). It was understood that the behavior of Tsallis entropy is opposite to Renyi and SURE entropies with respect to entropy indexes. In all the entropies, more transition of entropies from subband D4 to D5 was observed for Coif4 and Dmey wavelets (refer second and third column ofFig. 5).Collectively, entropies were higher in sub-bands D2,D3, and D4 for all the entropies except for sigmoid. It was clear that entropies start decreases as decomposition length goes down (reverse in case of sigmoid). Smooth transition in entropies over decomposition length between sub-bands was observed in case of Haar and Sym4 wavelets. The higher time complexity in case of Dmey wavelet was observed as compared to the other three wavelets.Wilcoxon rank sum test showedP<0.01 between normal and epileptic EEG entropies for all the wavelets and sub-bands except for sub-band A7.

Classification results using RMCH database

Fig. 6shows the classification accuracy using MODWT with different entropies (sigmoid, Shannon,and wavelet) for different decomposition levels and mother wavelets. Sigmoid entropy with Haar wavelet in sub-band D4 showed the highest classification accuracy of 98.44%. In addition, Haar wavelet in subband D3 (98.20%) and Sym4 wavelet in sub-band(97.96%) showed the best performance. The results obtained in other sub-bands were close to the best performance.

In the case of Shannon entropy, the highest classification accuracy of 98.02%, 97.44%, 97.08%,and 97.74% was obtained in sub-band D4 using Haar,Coif4, Dmey and Sym4 wavelets respectively.Wavelet entropy showed the highest accuracy of 96.80% in sub-band D4 using Haar wavelet. In the case of wavelet entropy, poor performance was observed in Coif4 and Dmey wavelets. The least classification accuracy was observed in sub-band A7 for sigmoid and Shannon entropy. However, wavelet entropy showed the least performance in sub-band D1.

Fig. 7depicts the classification accuracy obtained for Renyi entropy using different entropy indexes.Again, Haar and Sym4 wavelets were performed better in sub-bands D3 and D4. We observed that accuracy slightly was decreased as the entropy index increased. The best results of 97.73% were obtained in D4 sub-band using Haar wavelet for Renyi entropy with α =2. Similar classification results observed for Tsallis entropy (Fig. 8) using α =1.5 and 3. However,Tsallis entropy with α =5 performed worse in D1, D2,D3, and D4 sub-bands and highest of 97.31% obtained in D7 sub-band using Haar wavelet. SURE entropy with ε =1,3, and 5 produced accuracy of 97.87%,97.99%, 97.75% in sub-band D4 using Haar wavelet respectively (Fig. 9). No significant difference was observed for higher ? in all the wavelets. Across these results, SURE entropy with ε =5 was better in terms of results when compared with higher entropy index among other entropies. Collectively, results in subband D4 were excellent among all the entropies and wavelets. Quantitatively, lower decomposition levels appear to provide better classification results which are acceptable for clinical use. In terms of revealing dynamic characteristics, complexity and classification results, MODWT configured using Haar waveletbased sigmoid entropy outperformed other entropies.

Classification results using UBonn database

UBonn EEG data was classified using 10-fold cross-validation for classification problems, namely{A}-{E}, {ACD}-{E}, {ABCD}-{E}, and {AB}-{CD}-{E}. The experiment was conducted using all four wavelets and variants of entropies as similar to RMCH. Only the best results (Haar wavelet) using all the four wavelets are presented inFig. 10.Both Sigmoid and Shannon entropies showed the highest specificity, sensitivity, and accuracy of 100% using Haar wavelet in sub-band D5 for classification problem {A}-{E} (Fig. 10A). Further, Renyi entropy with α = 2, Tsallis entropy with α = 1.5 and SURE entropy with ε =5 showed the best results among different entropy index values. The sensitivity obtained by wavelet and SURE entropies was higher in sub-band A7 as compared to the other sub-bands.However, poor specificity was shown by the same entropies in sub-band A7.

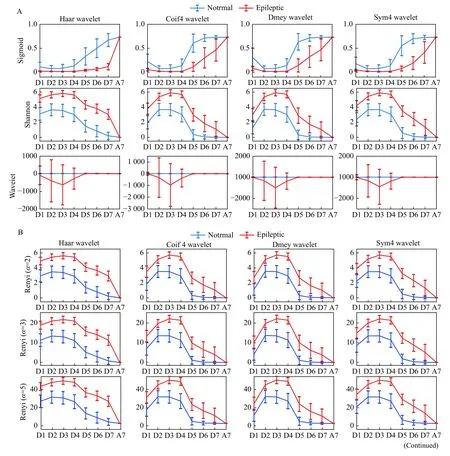
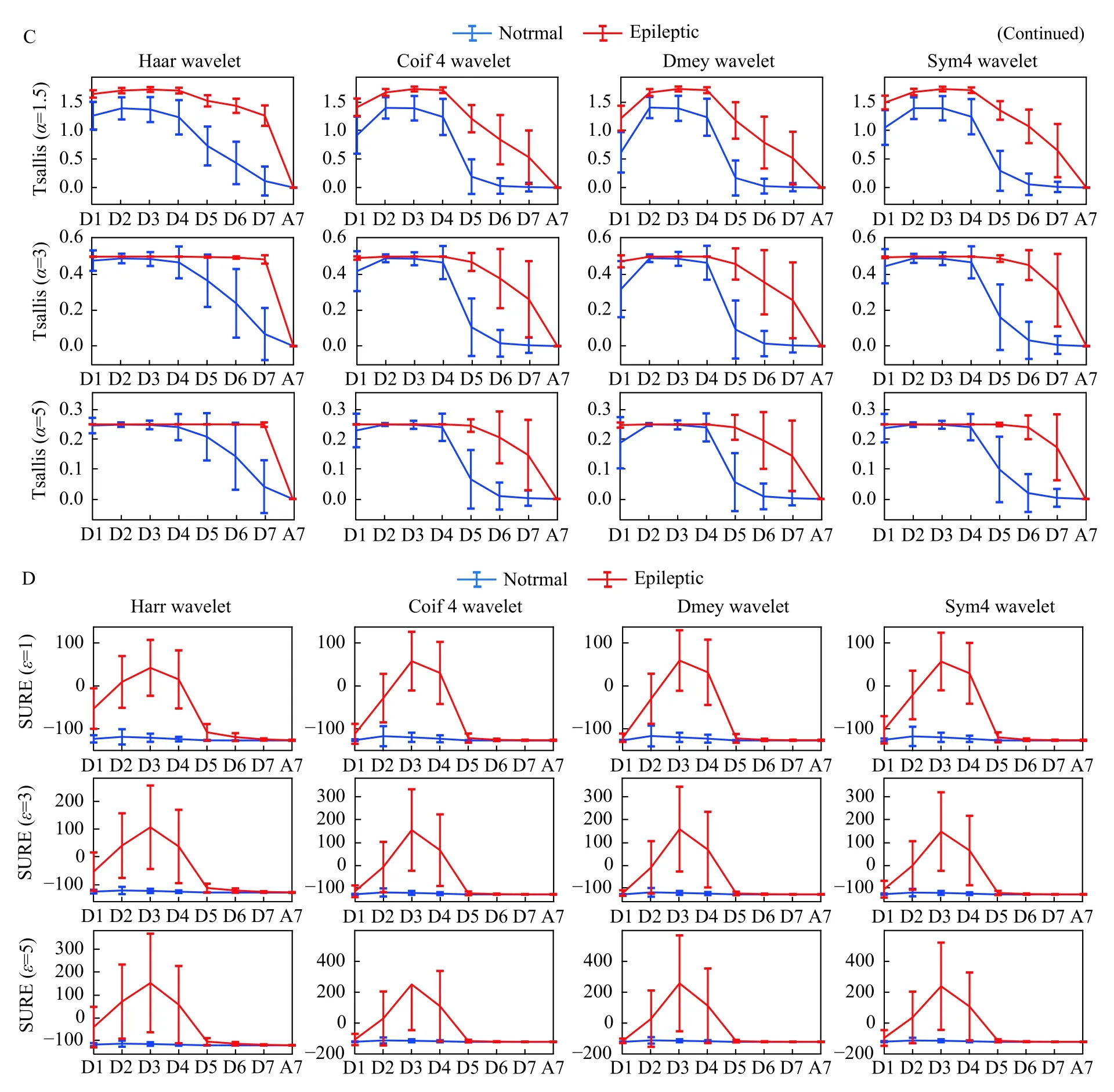
Fig. 5 Effects of MODWT decomposition length on entropies. A: first row: sigmoid entropy; second row: Shannon entropy; third row:wavelet entropy. B: first row: Renyi entropy (α =2); Second row: Renyi entropy (α =3); third row: Renyi entropy (α =5). C: first row: Tsallis entropy (α =1.5); second row: Tsallis entropy (α =3); third row: Tsallis entropy (α =5). D: first row: SURE entropy (ε =1); second row:SURE entropy (ε =3); third row: SURE entropy (ε =5). In all the sub figures, first column: entropies of Haar wavelet; second column: entropies of Coif4 wavelet; third column: entropies of Dmey wavelet; fourth column: entropies of Sym4 wavelet.

For the classification problem {ACD}-E, the good results were achieved using sub-bands D1 to D5, and the highest accuracy of 96.43% in sub-band D2(Fig. 10B). The highest accuracy of 94.06% was shown by sub-band D5 using sigmoid entropy for classification problem {ABCD}-{E} (Fig. 10C).Tsallis entropy with α=3 and 5 showed poor performance in all the sub-bands except for D4 and D5. Similarly, for three class classification problem{AB}-{CD}-{E}, all the entropies showed the accuracy of around 91.00% in sub-bands D1 and D2(Fig. 10D). We found that accuracy was decreasing as the decomposition level of MODWT goes deeper.Notably, good sensitivity was seen in sigmoid entropy using sub-band A7 but not in other entropies. In contrast, good specificity was observed in all the entropies in sub-band A7 except for sigmoid entropy.Overall, sigmoid and Shannon entropies outperformed other entropies in terms of classification results using the wavelets and sub-bands.

Classification results using CHB-MIT database

Fig. 6 Classification results shown by MODWT based entropies for different decomposition levels and wavelets. Left column: sigmoid entropy; middle column: Shannon entropy; right column: wavelet entropy. Legend indicates the decomposition levels of MODWT.

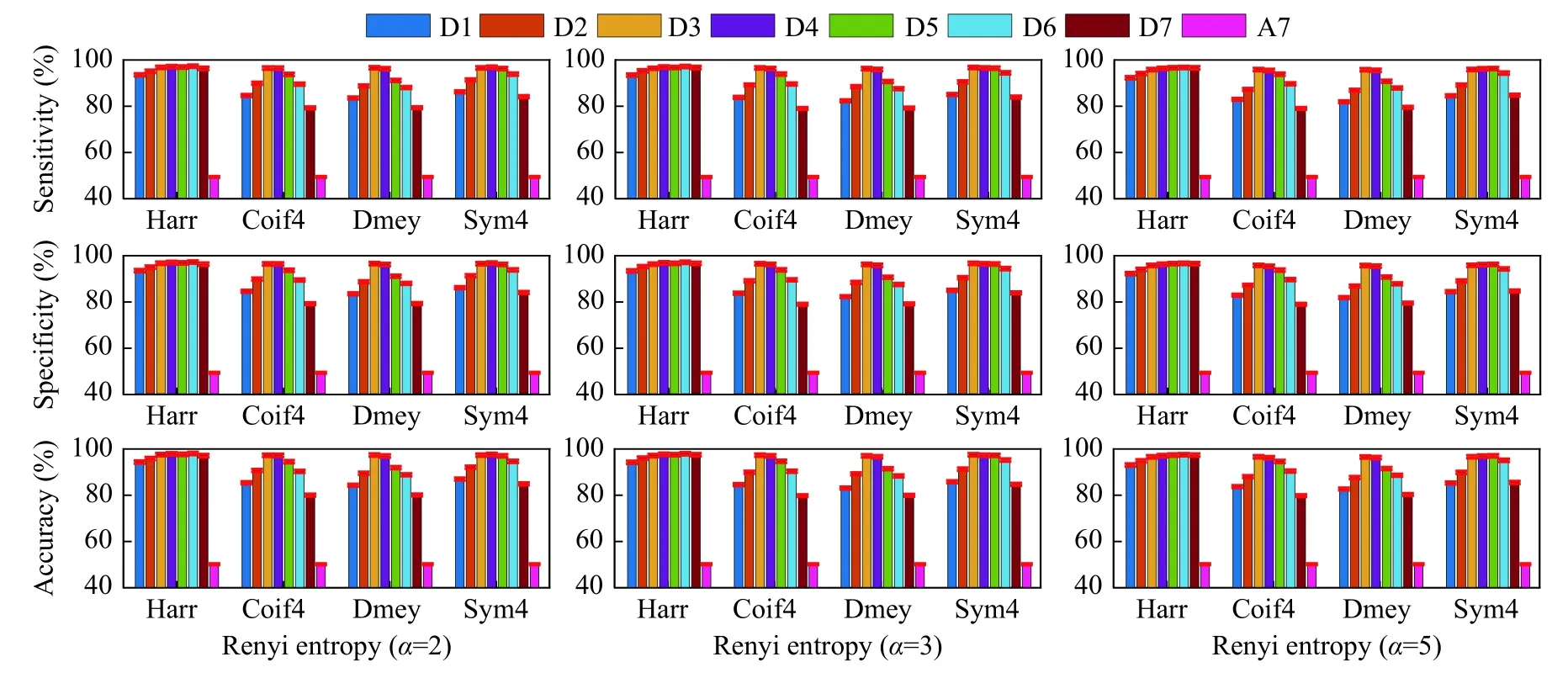
Fig. 7 Classification results shown by MODWT based Renyi entropy for different decomposition levels and wavelets. Left column:Renyi entropy ( ε =1); middle column: Renyi entropy ( α =3); right column: Renyi entropy ( α =5). Legend indicates the decomposition levels of MODWT.

Fig. 11depicts the classification results obtained for CHB-MIT database using Haar wavelet (found to be best) using all the six entropies. Due to the higher sampling rate of 256 Hz, CHB-MIT database was decomposed until level 10. Interestingly, all the entropies using Haar wavelet in sub-band D6 performed better leading the highest sensitivity specificity and accuracy of 96.62%, 96.67%, and 94.51%, respectively. Again, as similar to RMCH and UBonn databases, the least results obtained in subband A10 (i.elast level) using all the entropies.Further, results obtained in sub-bands D5 and D7 were close to D6. The above results conclude that the proposed method performs better on different EEG databases.

Discussion

In this paper, we have investigated the complexity analysis and dynamic characteristics of EEG signals using MODWT and six entropies for identification of seizure onset. To carry out this objective, EEG signals were decomposed using MODWT until level 7.Further, six entropies were estimated in each sub-band to classify using SVM classifier.

As we have already discussed, MODWT is an improved version of DWT without orthogonality.MODWT does not apply the decimation and the coefficients in each level remain the same length being non-decimated DWT[29]. MODWT offers several advantages over the DWT which are discussed here. The redundancy property of the MODWT facilitates the arrangement of the decomposed coefficients at each level with the original time series,thus enables comparison between the original series and its decomposition[29–30]. The coefficients of MODWT multiresolution analysis are associated with zero phase filters which result in a more asymptotically efficient wavelet variance estimator than the DWT[29]. Further, it is transform invariant,since a shift in the signal does not change the pattern of the wavelet transform coefficients. Finally,MODWT is energy conserving, it is well suited for analyzing the scale dependence of variability[29–30].With the influence of the above facts, MODWT outperformed DWT in terms of classification results.

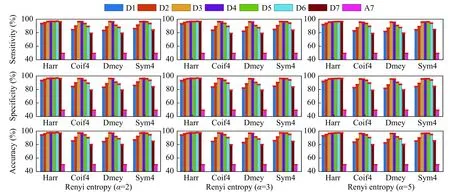
Fig. 8 Classification results shown by MODWT based Tsallis entropy for different decomposition levels and wavelets. Left column:Tsallis entropy ( α =1.5); middle column: Tsallis entropy ( α =3); right column: Tsallis entropy ( α =5). Legend indicates the decomposition levels of MODWT.

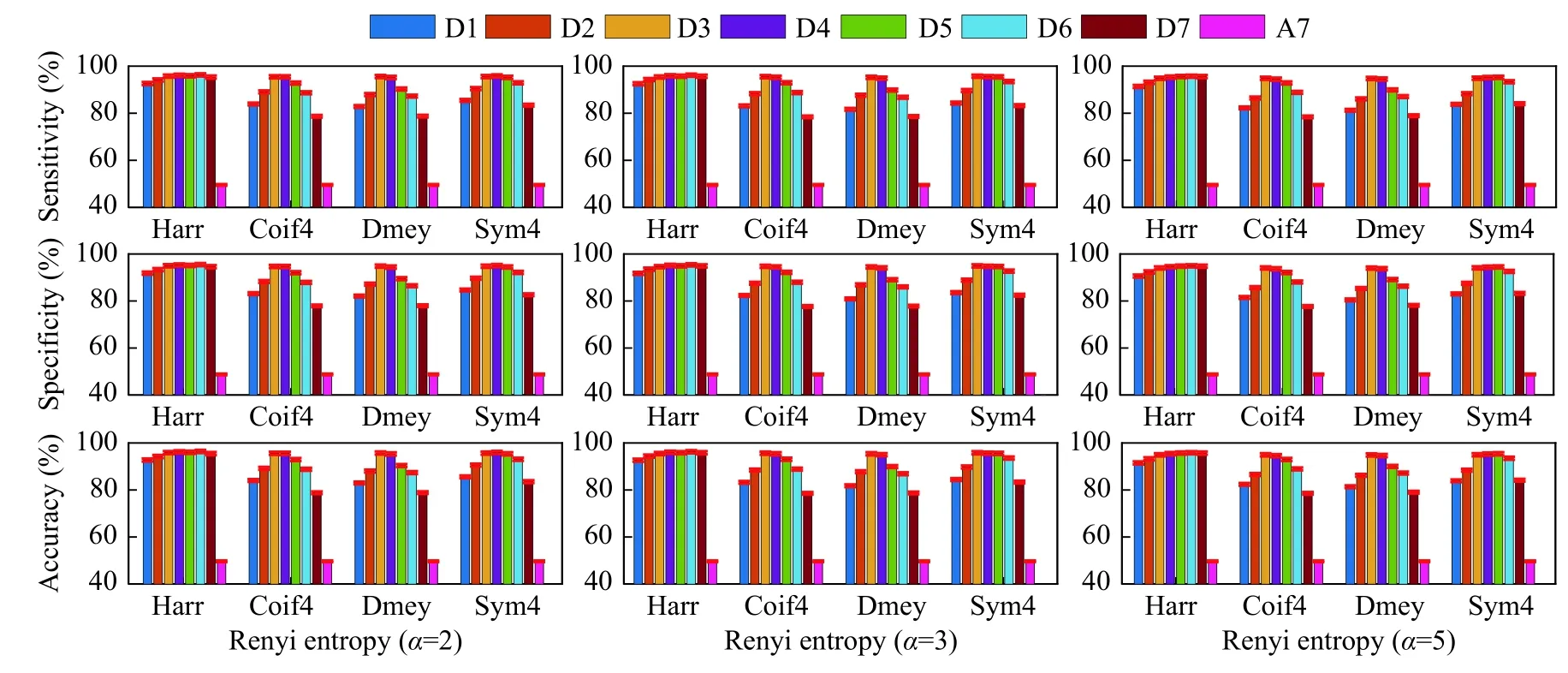
Fig. 9 Classification results shown by MODWT based SURE entropy for different decomposition levels and wavelets. Left column:SURE entropy ( ε =1); middle column: SURE entropy ( ε =3); right column: SURE entropy ( ε =5). Legend indicates the decomposition levels of MODWT.

We have compared the results of MODWT versus DWT using the same wavelets and features to highlight the advantages of MODWT. The performance of the MODWT results was compared using the RMCH database. The EEG signals were decomposed into five levels and results from the best sub-bands were reported inSupplementary Fig. 1(available online). The classification results showed that MODWT outperformed DWT. The Wilcoxon rank-sum test delivered the statistical difference ofP<0.01 between the accuracy of MODWT and DWT for sigmoid and wavelet entropy. In addition,P<0.05 shown for other entropies, thus it indicates MODWT based features greatly improve the classification results. The above analysis is evident that the property of MODWT over DWT has the advantage of capturing more significant information from EEGs.

Supplementary Table 1(available online) shows the comparison results with other existing methods.The studies considered for the comparison based on the criteria that the EEG time series have been decomposed using either DWT or MODWT. One should notice that the EEG recordings used in their study are different and exact comparison cannot be performed. The studies[23,46]that have used EEG recordings from the UBonn yielded accuracy close to 100% due to the clean EEG provided in the database.In the study of Li MYet al, the highest classification accuracy of 100% was shown using Sym8 wavelet using MODWT[23]. The study also showed MODWT outperformed DWT in terms of classification results and computation time. Further, the wavelet-based nonlinear similarity index showed better performance in beta (10–30 Hz) frequency band[24]. The results reported in many studies[31,46–48]have shown DWT suits well for seizure detection but MODWT has not explored. However, the proposed study using MODWT and six entropies showed excellent results.In particular, MODWT with sigmoid entropy outperformed other entropies among all the four wavelets.

Supplementary Fig. 2(available online) depicts the computational time required for pre-processing,MODWT, feature extraction, and classification procedure of the proposed technique using RMCH database. The results considered for comparison that was performed better among different sub-bands in respective entropies and wavelets. Individually, the computational time taken by sigmoid entropy in all the wavelets was found to be slightly less. Further,wavelet entropy was slightly computationally expensive when compared with other entropies.Overall, Haar wavelet and Dmey wavelets were computationally economically and expensive respectively. The proposed method was implemented on MATLAB 2018b using 8GB RAM, CPU 2 GHz with an Intel I3 processor.

The overall performance of the proposed technique was assessed using relative performance[11]. Relative performance is defined as the ratio of the classification accuracy to the computation time (second) and it is given by,

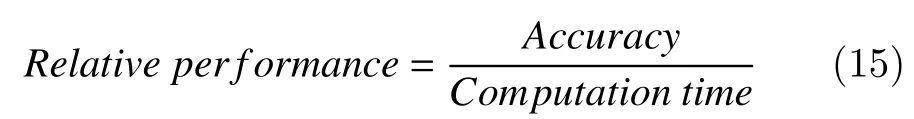
It can be speculated from the above equation that efficiency of the model indicated by higher relative performance.Supplementary Fig. 3(available online)shows the best relative performance obtained among all the wavelets and entropies. We observed that sigmoid entropy using Haar wavelet yielded better relative performance among all. Further, Dmey wavelet showed the least relative performance when compared to other wavelets.

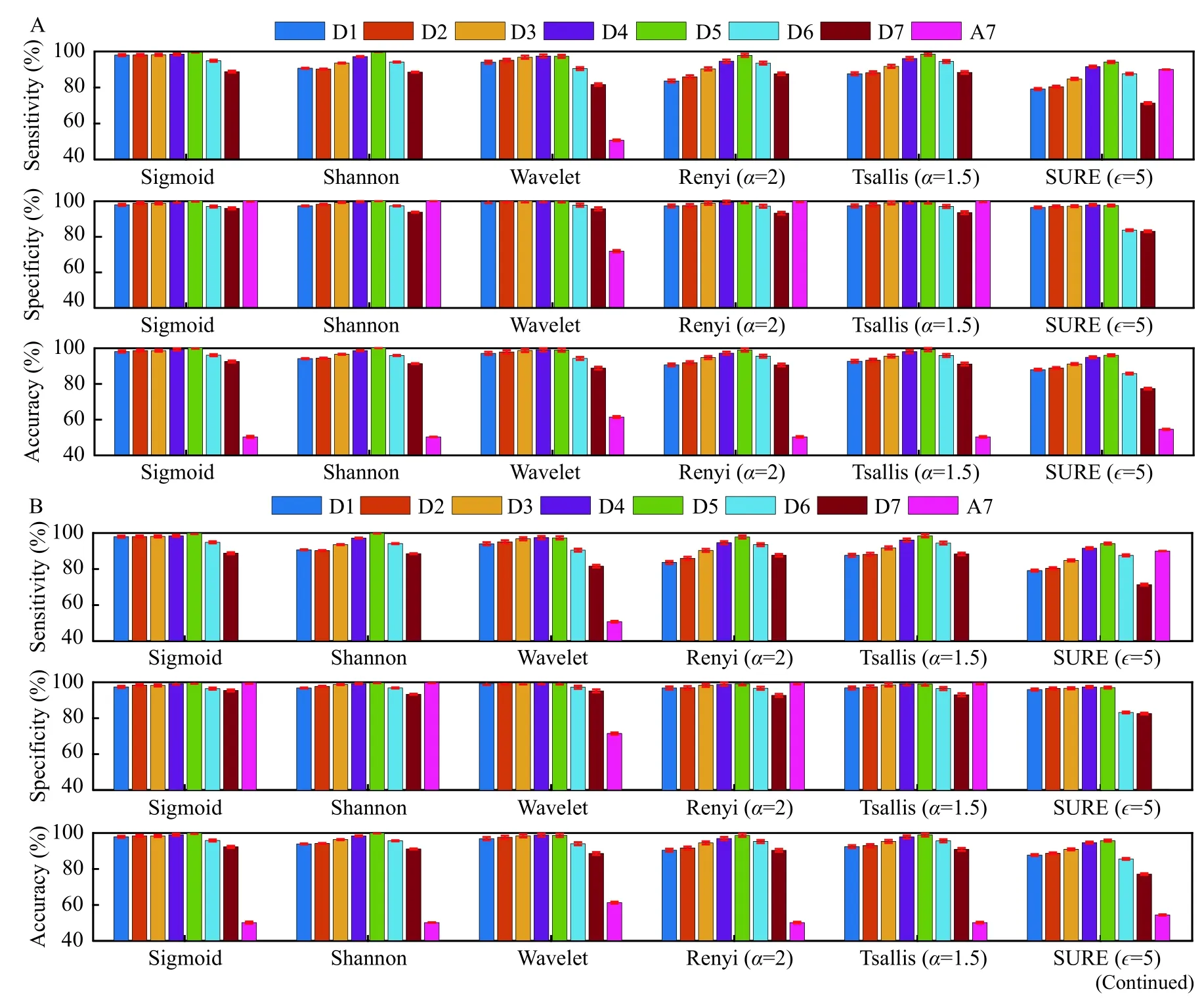
Fig. 10 Classification results shown by MODWT based entropies with Haar wavelet for UBonn database. Legend indicates the decomposition levels of MODWT. Classification problem A: {A}-{E}, B: {ACD}-{E}, C: {ABCD}-{E}, and D: {AB}-{CD}-{E}.

Significant findings of the study

The application of MODWT revealed that the energy content in the sub-bands D2, D3, and D4 were significantly high as compared to the other levels for all the wavelets in case of RMCH database. We observed, sigmoid entropy lower for epileptic and higher for normal EEG. Further, Renyi and SURE entropies were found to be increasing as entropy index αand ε went higher respectively. Tsallis entropy was seen to be decreasing as the entropy index increases.In most of the cases, least classification accuracy was observed using the last level of approximation coefficients A7 (for RMCH and UBonn) and A10(CHB-MIT). Overall, our study suggests that entropy index values of Renyi, Tsallis, and SURE entropies must be selected carefully.

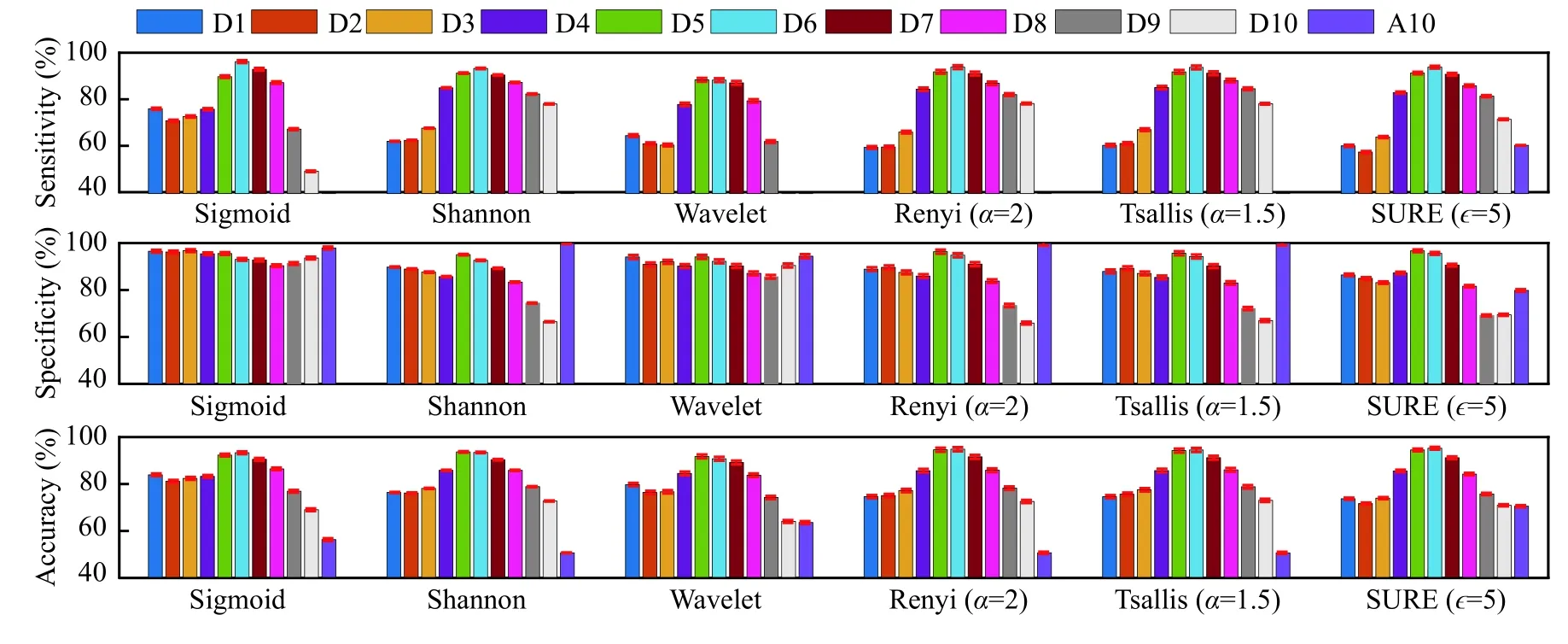
Fig. 11 Classification results are shown by MODWT based entropies for CHB-MIT database. The legend indicates the decomposition levels of MODWT.

As a future expansion, the study will be extended on larger EEG databases using the best MODWT subband and entropy. Further, deep learning neural network will be explored along with the classification of seizure types.

In this paper, complexity analysis and dynamic characteristics of epileptic EEG were studied using MODWT based entropies and classified using SVM classifier. Experimental results suggest that sigmoid entropy outperformed other entropies using all the wavelets. Collectively, results demonstrate that different mother wavelets have an impact on computational time, but not much on classification results in the same sub-band. Extensive insight into the wavelet analysis on RMCH database showed that energy content in the sub-bands D2, D3, and D4 is high and highest classification accuracy shown by the same. Furthermore, the entropies in sub-bands D2,D3, and D4 are significantly high for all the entropies except for sigmoid entropy. Sigmoid entropy produced the highest classification results of 98.44%using Haar wavelet in sub-band D4 for RMCH database. Further, the highest accuracy of 100% and 94.51% was achieved for UBonn and CHB-MIT databases respectively. We found that Haar and Dmey wavelets were computationally economical and expensive respectively. The proposed study suggests that entropy index in Renyi, Tsallis, and SURE entropies must be chosen properly.

Acknowledgments

The authors are grateful to clinical doctors of Institute of Neuroscience, Ramaiah Medical College and Hospitals, Bengaluru, India, for valuable discussion and providing EEG recordings for research purpose.