◇ 浙江 王茂聰

函數(shù)是數(shù)學(xué)大廈的基石,也是高中數(shù)學(xué)的核心內(nèi)容.高考對函數(shù)的要求一向很高,除了要求考生掌握基本問題的解法外,往往還滲透一些創(chuàng)新性問題,這類問題既考查了考生融會貫通的綜合能力,同時也檢驗了考生勇于探究的學(xué)習(xí)品質(zhì).這類問題新穎獨特,本文列舉幾例,與大家共賞.

1 三次函數(shù)拐點的應(yīng)用

三次函數(shù)是最常見的高次函數(shù),也是高考命題經(jīng)常涉及的函數(shù).而三次函數(shù)拐點的概念,在中學(xué)教材中未曾提及,題目中給出函數(shù)的概念,并要求學(xué)生利用這個概念解決相關(guān)問題,可以全面考查學(xué)生的學(xué)習(xí)力.

例1對于三次函數(shù)f(x)＝ax3＋bx2＋cx＋d(a≠0),給出如下定義:

設(shè)f′(x)是函數(shù)y＝f(x)的導(dǎo)數(shù),f″(x)是函數(shù)f′(x)的導(dǎo)數(shù),若方程f″(x)＝0有實數(shù)解x0,則稱點(x0,f(x0))為函數(shù)y＝f(x)的“拐點”.

某同學(xué)經(jīng)過探究發(fā)現(xiàn):任何一個三次函數(shù)都有“拐點”;任何一個三次函數(shù)都有對稱中心,且“拐點”就是對稱中心.給定函數(shù)

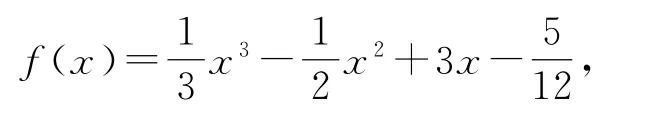
請你根據(jù)上面探究結(jié)果,計算

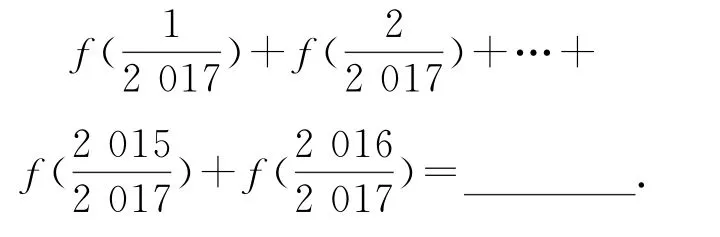
解析

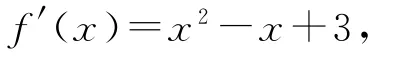
故f″(x)＝2x－1.

令f″(x)＝0可得,所以函數(shù)f(x)的拐點即對稱中心為(),若x1＋x2＝1,則

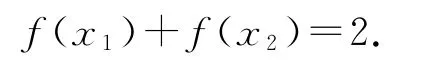
所以

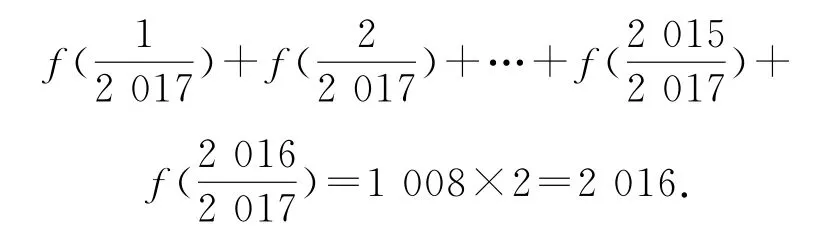
點評

本題屬于背景新穎的材料分析題,要求考生從材料中讀取有關(guān)信息,解決問題.本題既考查了導(dǎo)數(shù)的應(yīng)用,又考查了三次函數(shù)的對稱性,題干創(chuàng)新獨特,能靈活考查學(xué)生利用數(shù)學(xué)知識解題的本質(zhì),即轉(zhuǎn)化思想.

2 抽象函數(shù)值的大小比較

抽象函數(shù)是高中函數(shù)的難點,與抽象函數(shù)有關(guān)的不等式問題一般會涉及函數(shù)的單調(diào)性,而抽象函數(shù)的單調(diào)性又與導(dǎo)數(shù)有著密切的聯(lián)系,于是這種綜合性極強并要求考生具有構(gòu)造思想的數(shù)學(xué)問題應(yīng)運而生.

例2設(shè)函數(shù)f(x)的導(dǎo)函數(shù)為f′(x),對任意x∈R都有f(x)＞f′(x)成立,則( ).

A.3f(ln 2)＜2f(ln 3)

B.3f(l n 2)＝2f(l n 3)

C.3f(ln 2)＞2f(ln 3)

D.3f(l n 2)與2f(l n 3)的大小不確定

解析

由題意對任意x∈R都有f(x)＞f′(x),所以g′(x)＜0,即g(x)在R上單調(diào)遞減.

又由l n 2＜l n 3,可知g(l n 2)＞g(l n 3),即

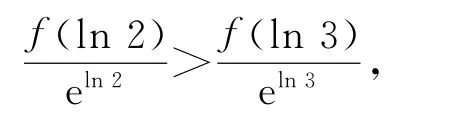
點評

抽象函數(shù)值的大小比較既是一類新穎題,又是一類難題.恰當(dāng)構(gòu)造函數(shù),并利用函數(shù)的單調(diào)性比大小是解決這類問題的通法.本題求解的關(guān)鍵是利用已知條件構(gòu)造恰當(dāng)函數(shù),考查了對數(shù)運算公式的應(yīng)用.

3 新定義函數(shù)問題

新定義問題是數(shù)學(xué)中最常見的創(chuàng)新題,新定義函數(shù)問題給出一個函數(shù)的新名稱,同時給出該函數(shù)獨特的性質(zhì),要求考生利用新函數(shù)的新性質(zhì)去解決相關(guān)問題.

例3若函數(shù)f(x)是定義域D內(nèi)的某個區(qū)間I上的增函數(shù),且在I上是減函數(shù),則稱y＝f(x)是I上的“單反減函數(shù)”,已知f(x)＝l nx,.

(1)判斷f(x)在(0,1]上是否是“單反減函數(shù)”;

(2)若g(x)是[1,＋∞)上的“單反減函數(shù)”,求實數(shù)a的取值范圍.

解析

(1)由于f(x)＝l nx在(0,1)上是增函數(shù),且,因為

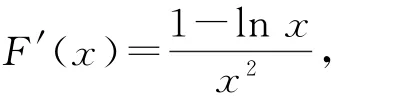
所以x∈(0,1)時,F′(x)＞0,F(x)為增函數(shù),所以f(x)在(0,1)上不是“單反減函數(shù)”.

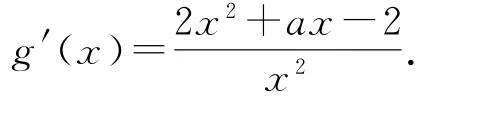
因為g(x)是[1,＋∞)上的“單反減函數(shù)”,則g′(x)≥0在[1,＋∞)上恒成立,所以g′(1)≥0,即在[1,＋∞)上是減函數(shù),所以G′(x)≤0在[1,＋∞)上恒成立,即在[1,＋∞)上恒成立,即axaxl nx－4≤0在[1,＋∞)上恒成立.

令p(x)＝ax－axl nx－4,求導(dǎo)得

p′(x)＝－alnx≤0,

故p(x)＝ax－axl nx－4在[1,＋∞)上是減函數(shù),pmax(x)＝p(1),由p(1)≤0得a≤4.

綜上,a的取值范圍為[0,4].

點評

本題的新穎之處是給出新定義“單反減函數(shù)”,考查學(xué)生對新定義的認(rèn)識;其次,本題需要利用導(dǎo)數(shù)解決新定義函數(shù)的有關(guān)問題,考查新定義的應(yīng)用.本題表面上看是函數(shù)新問題,但解決此問題的方法還是研究函數(shù)單調(diào)性的老方法——導(dǎo)數(shù)法.可謂“以舊破新”.

創(chuàng)新,是一個民族的靈魂,也是數(shù)學(xué)的靈魂.數(shù)學(xué)教育要創(chuàng)新,數(shù)學(xué)問題也要創(chuàng)新,這是中學(xué)數(shù)學(xué)發(fā)展的必由之路,也是培養(yǎng)數(shù)學(xué)創(chuàng)新思維的有效途徑之一.