The gravity impact in a rotating micropolar thermoelastic medium with microtemperatures
Mohmed I.M.Hill ,Rmdn S.Tntwi ,Mohmed I.A.Othmn
a Department of Mathematics, Faculty of Science, P.O.Box 44519, Zagazig University, Zagazig, Egypt
b Department of Basic Science, Faculty of Engineering, Sinai University, Al-Arish, Egypt
Abstract
Keywords: Gravity;Micropolar thermoelasticity;Microtemperatures;Rotation.
1.Introduction
The linear theory of elasticity has an essential importance in the stress analysis of steel,which is the commonest engineering,structural material;this theory describes the mechanical behavior of the common solid materials,e.g.,concrete,wood and coal.In the case of elastic vibrations characterized by high frequencies and small wavelengths,the influence of the body microstructure becomes significant.Metals,polymers,composites,soils,rocks and concrete are typical media with microstructures.Most of the natural and man-made materials,as engineering,geological,and biological media possess a microstructure.The micropolar elasticity theory takes into consideration the granular character of the medium applied to materials for which the ordinary classical theory of elasticity fails owing to the microstructure of these materials.Within this theory,solids can undergo macro deformations and microrotations;the motion of this kind of solids are completely characterized by the displacement vector and the microrotation vector.Eringen [1] extended the micropolar theory to include the thermal effects.Boschi and Ie?san [2] extended a generalized theory of micropolar thermoelasticity.The microtemperatures and the micro deformations of nanoparticles are very important in the future technologies.Recently,several continuum theories with microstructure are formulated.
A thermodynamic theory of the elastic materials with the inner structure,micro deformations,and the particles possess microtemperatures is proposed by Grot [3].The thermodynamics of a continuum with microstructure are extended with assuming that the microelements have different temperatures.The concept of microtemperatures is introduced to describe this phenomenon.The microtemperatures depend homogeneously on the micro coordinates of the microelements.Riha[4] presented a study of the heat conduction in materials with microtemperatures.Ie?san [5] investigated the concepts of the micropolar thermoelastic material having microtemperatures.Casas and Quintanilla [6] investigated the exponential stability in thermoelastic bodies with microtemperatures.Scalia and Svanadze [7] presented the solutions of the theory of thermoelasticity with microtemperatures.Ie?san [8] discussed thermoelastic bodies with microstructures and microtemperatures.Othman et al.[9-12] discussed interesting problems in thermoelasticity with microtemperatures,different mechanical,and thermal effects of micropolar thermoelasticity with microtemperatures.The propagation of plane waves in a rotating media is important in many realistic problems as the rotation of heavenly bodies and the moon.Schoenberg and Censor [13] established the propagation of the waves in a rotating,homogeneous,isotropic,and linear elastic medium for any orientation of the rotation axis with respect to free space taking into consideration the Coriolis and the Centripetal acceleration.Othman et al.[14,15] studied the effect of rotation on the porous thermoelastic material.
Bromwich [16] established the effect of the gravity,which is neglected in the classical theory of elasticity,on the wave propagation of an elastic medium.Othman and Hilal [17] investigated the effect of rotation and initial stress in thermoelastic material with voids.Othman et al.[18] and Othman and Hilal [19] studied the effect of the gravity field on thermoelastic materials.Marin et al.[20] discussed the qualitative results on mixed problems of micropolar bodies with microtemperatures.Abd Elaziz and Hilal [21] discussed the influence of Thomson effect and inclined loads in electromagneto-thermoelastic solid with voids under Green-Naghdi theories.
The main objective of the present work is to investigate the variation of the physical quantities in the problem for a homogenous,isotropic,micropolar thermoelastic medium with microtemperatures analytically for different cases.The physical quantities represented graphically.
2.The basic equations and formulation of the physical problem with solution
Consider the linear theory of thermodynamics for isotropic elastic materials with inner structure.According to Eringen[1],Ie?san [8] and Schoenberg and Censor [13],the field equations and the constitutive relations for a homogeneous,isotropic micropolar thermoelastic medium with microtemperatures without body forces,body couples,heat sources,and first heat source moment,rotated with a uniform angular velocity,can be formulated as
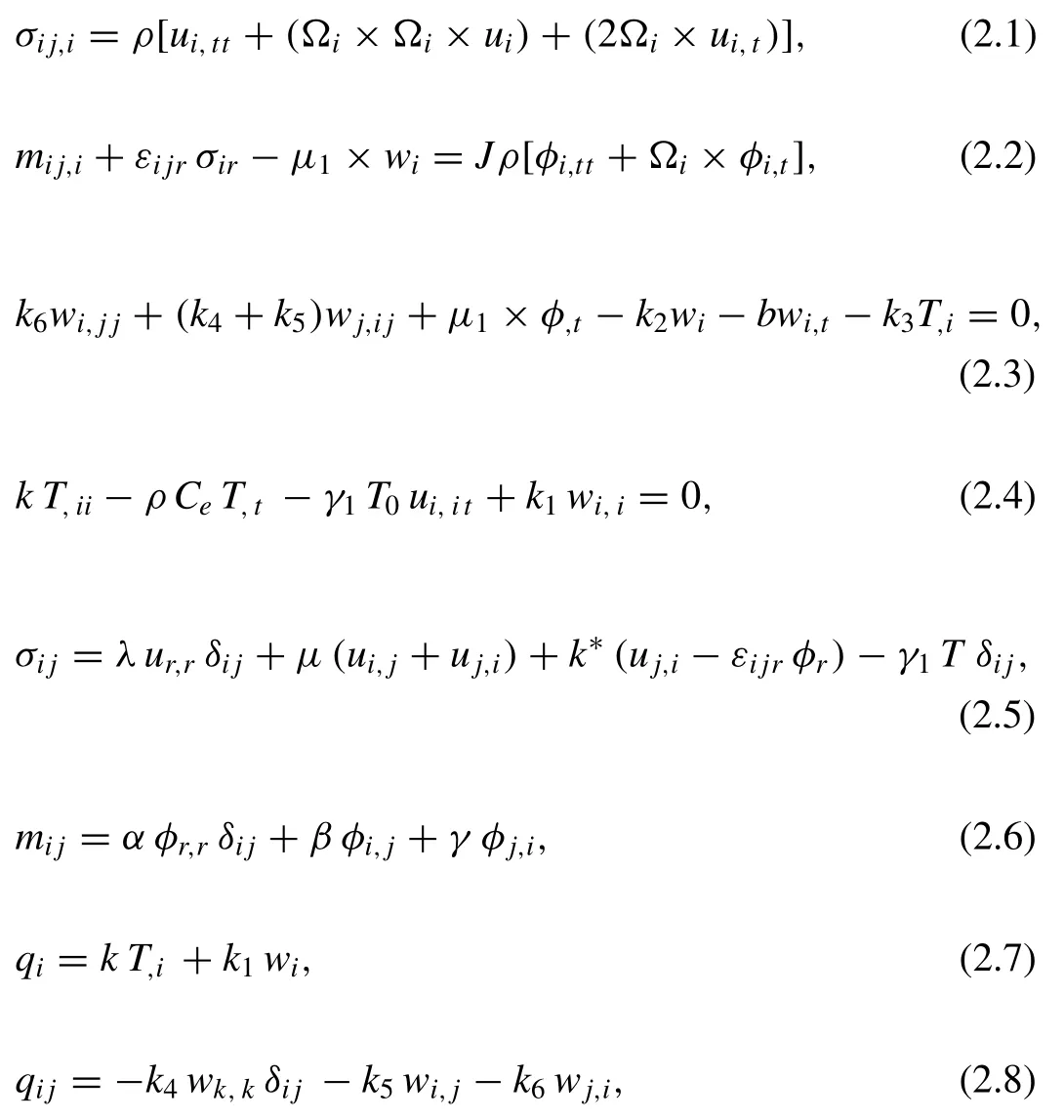
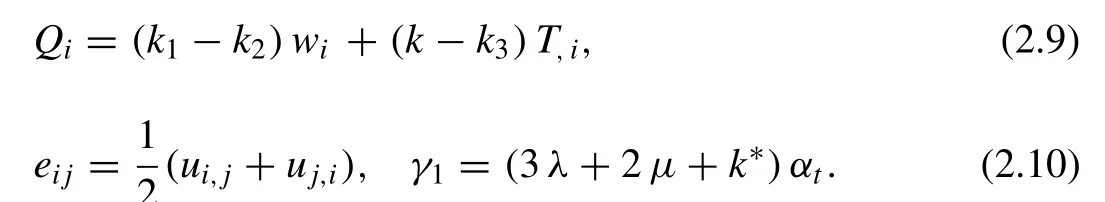
Where,λ,μare the Lamé constants,α,β,γandk?are the micropolar constants,αtis the linear thermal expansion coefficient,ρis the density,Ceis the specific heat at constant strain,kis the thermal conductivity,uiis the displacement vector,Tis the absolute temperature,T0is the reference temperature chosen so that(T?T0)/T0|<<1,φiis the microrotation vector,σijare the components of the stresses,eijare the components of strains,δijis the Kronecker delta,?ijris the permutation symbol,eis the dilation,Ωis the uniform angular velocity,mijis the couple stresses,Jis the microinertia,wiis the microtemperatures vector,μ1,b,ki(i=1,2,...,6)are the constitutive coefficients,qijis the heat flux moment,qiis the first heat flux moment andQiis the mean heat flux vector.
Consider an isotropic linear homogeneous micropolar thermoelastic medium with micro-temperatures and a half-space(y≥0),the rectangular Cartesian coordinate system (x,y,z)originated on the surfacez=0.For 2-D problem;the dynamic displacement vectorui=(u,v,0),the medium rotated with a uniform angular velocityΩi=(0,0,Ω),and the microrotation vectorφι=(0,0,φ3).Then the microtemperatures vector iswi=(w1,w2,0).All quantities considered will be functions of the time variabletand the coordinatesxandy.In the used equations a dot denotes differentiation with respect to time,while a comma denotes material derivatives;Eqs.(2.1)-(2.4) under the gravity will be:


where g is the acceleration due to the gravity.
Define the non-dimensional variables by expressions:
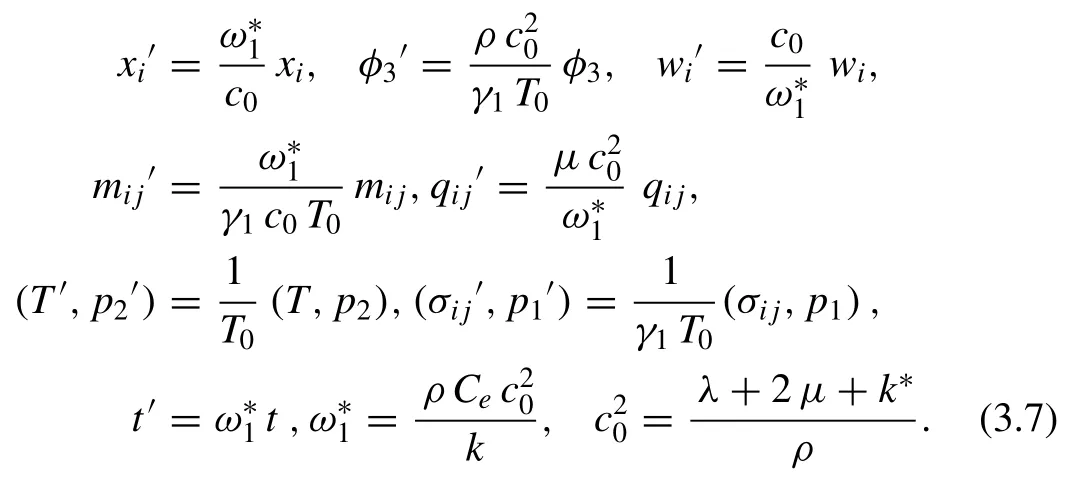
Assuming the potential functionsψ1(x,y,t),ψ2(x,y,t),q1(x,y,t) andq2(x,y,t),in dimensionless forms
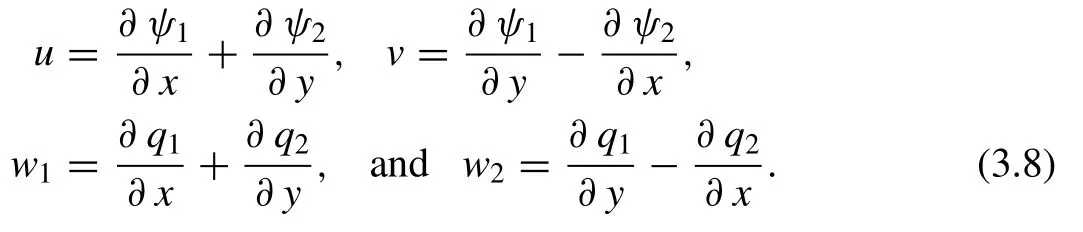
To get the expression for the physical quantities,consider the solution in the form
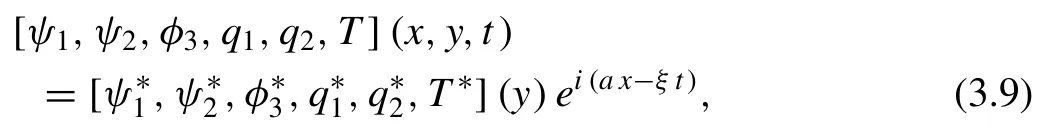
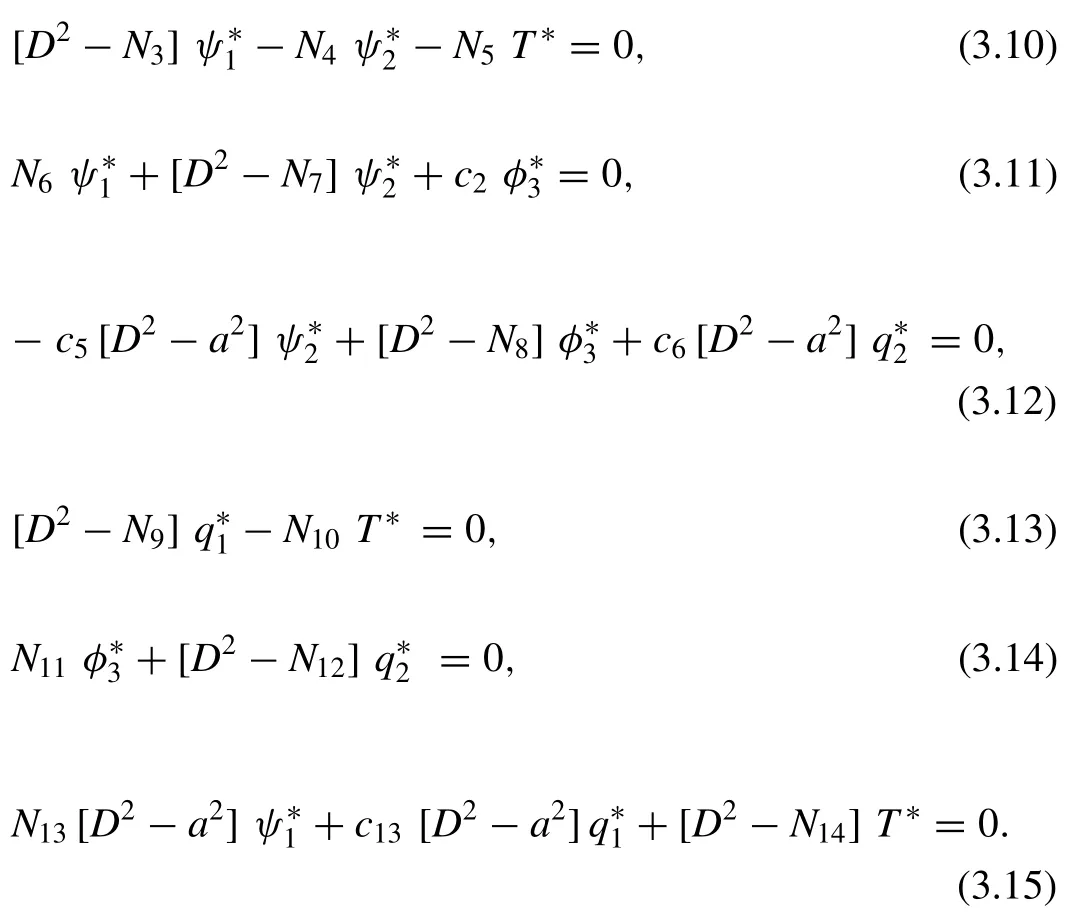
All the constants are given in Appendix.EliminateandT?among Eqs.(3.10)-(3.15),to obtain the following differential equation
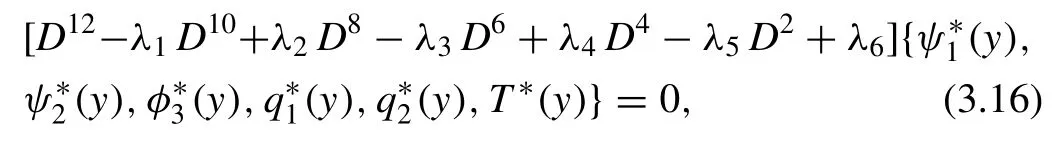
whereλn(n=1,2,...,6)can be obtained from eliminating the functions between Eqs.(3.10)-(3.15),while the Eq.(3.16) can be factored as
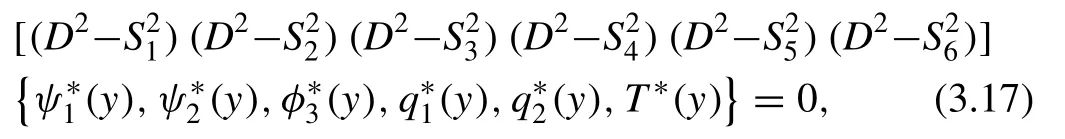
where(n=1,2,...,6)are the roots of the characteristic equation of Eq.(3.16).
The general solution of Eq.(3.16),which are bound aty→ ∞,is given by
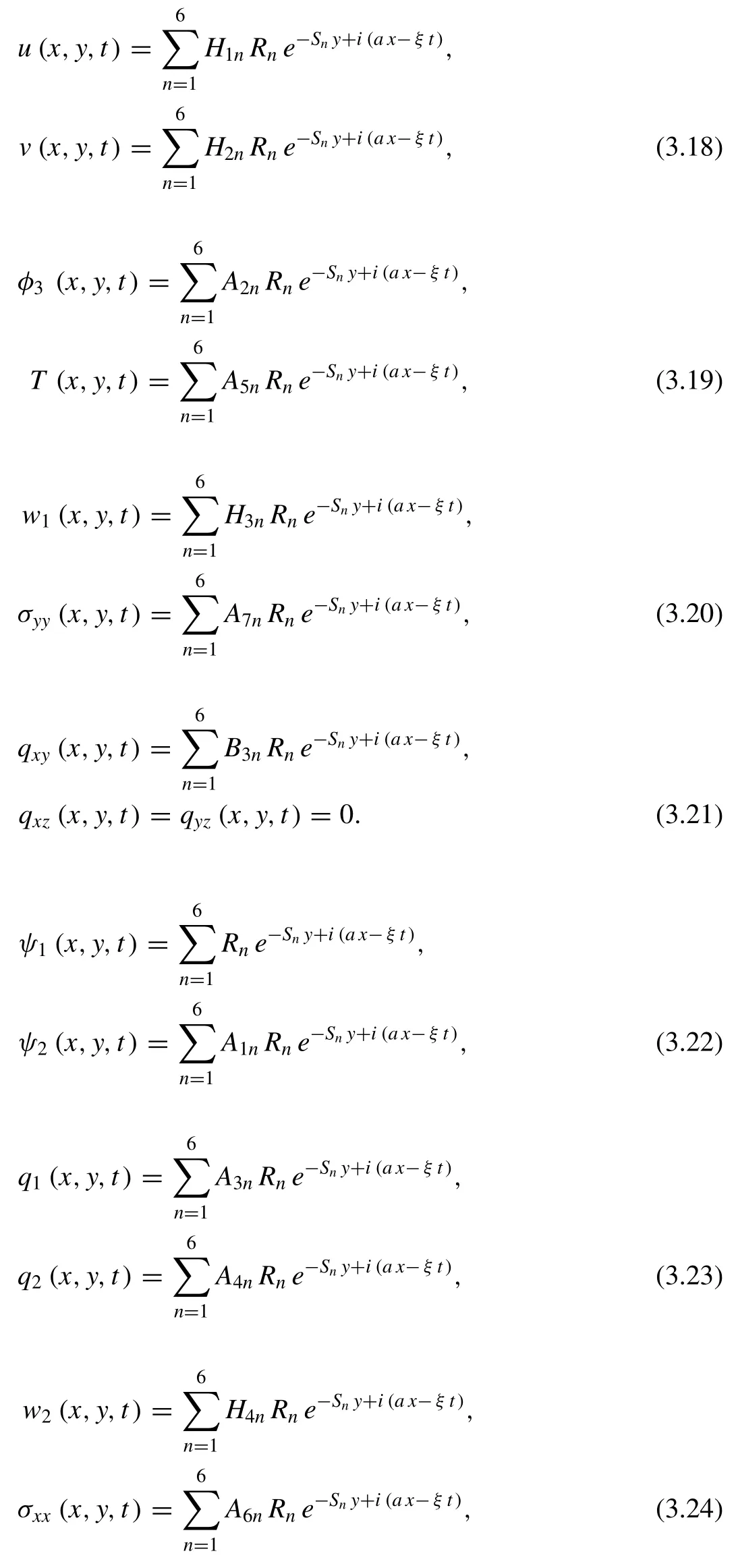
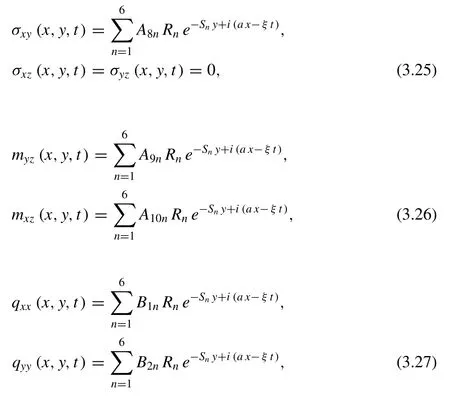
whereRn(n=1,2,...,6)being coefficients.
3.Boundary conditions
Consider the following boundary conditions to determine the constantsRn(n=1,2,...,6)and ignore the positive exponentials to avoid the unbounded solutions at infinity.Then the surface of the medium aty=0 suggests these conditions
(a) The normal stress condition,mechanically stressed by constant forcep1,then

(b) The tangential stress condition,stress free,i.e.,

(c) The condition of the couple stress,the couple stress is constant iny?direction.This implies that

(d) The thermal condition,the half-space subjected to thermal shock applied to the boundary,leads to

wherep2is the applied constant temperature to the boundary.
(e) The normal and the tangential first heat flux moments are free,so that

Substituting the expressions of the considered quantities in these boundary conditions,to obtain the values of the constantsRn(n=1,2,...,6).Particularcases
In the present work we consider the following particular cases:
(i) Non-rotating medium:takingΩ=0 in Eqs.(2.1) and(2.2).
(ii) Absence of the gravity:takingg=0 in Eq.(2.1).
(iii) Absence of micropolar:takingα,β,γ,k?,j=0 in Eqs.(2.1) and (2.2).
4.Numerical results and discussion
To illustrate the obtained theoretical results;according to Eringen [22] the magnesium crystal-like thermoelastic micropolar material was taken,(SI units are used).
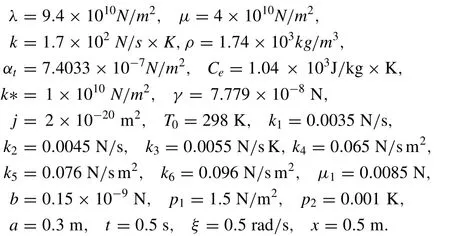
These numerical values are used to obtain the variation of the real parts of the displacementu,the microtemperature vectorw1,the temperatureT,the stressσyy,the microrotationφ3and the first flux momentqxywith the distancey.
Figs.1-6 represent the change in the behavior of the physical quantities against the distanceyin 2-D withg=9.8 m/s2,in the case ofΩ=0.4 rad/s,0.
Figs.7-12 show the behavior of the physical quantities against the distanceyin 2-D duringΩ=0.4 rad/s in the case ofg=9.8m/s2,andg=0.Figs.13-15 depict the variation of the physical quantities against distanceyin 2-D in the case of presence and absence of micropolar when the rotation and the gravity are present.
Fig.1 shows the variation of the displacement componentμwhich increases in the ranges 0 ≤y≤2,3 ≤y≤4.5,5.5 ≤y≤8 and 8.5 ≤y≤15,while it decreases in the ranges 2 ≤y≤3,4.5 ≤y≤5.5 and 8 ≤y≤8.5 with the increase of the rotation.
Fig.2 clarifies the variation of the microtemperatures vectorw1.It is seen thatw1decreases in the ranges 0 ≤y≤1,2.5 ≤y≤3.5,4.5 ≤y≤6,7 ≤y≤8,9 ≤y≤10.5,11.5≤y≤12.5 and 14 ≤y≤15,while it increases in the ranges 1 ≤y≤2.5,3.5 ≤y≤4.5,6 ≤y≤7,8 ≤y≤9,10.5 ≤y≤11.5 and 12.5 ≤y≤15 with the increase of the rotation.
It is clear that from Fig.3 the variation of the temperatureTincreases with the increase of the rotation through 0 ≤y≤15.
Fig.4 depicts the variation of the normal stressσyy,which increases with the increase of the rotation for 0 ≤y≤15.Fig.5 explains that the microrotation vectorφ3increases in the ranges 0 ≤y≤1,1.5 ≤y≤2.5,3.5 ≤y≤5,6 ≤y≤6.5,7 ≤y≤9 and 10 ≤y≤15 while it decreases in the ranges 1 ≤y≤1.5,2.5 ≤y≤3.5,5 ≤y≤6,6.5 ≤y≤7 and 7 ≤y≤10 with the increase of the rotation.
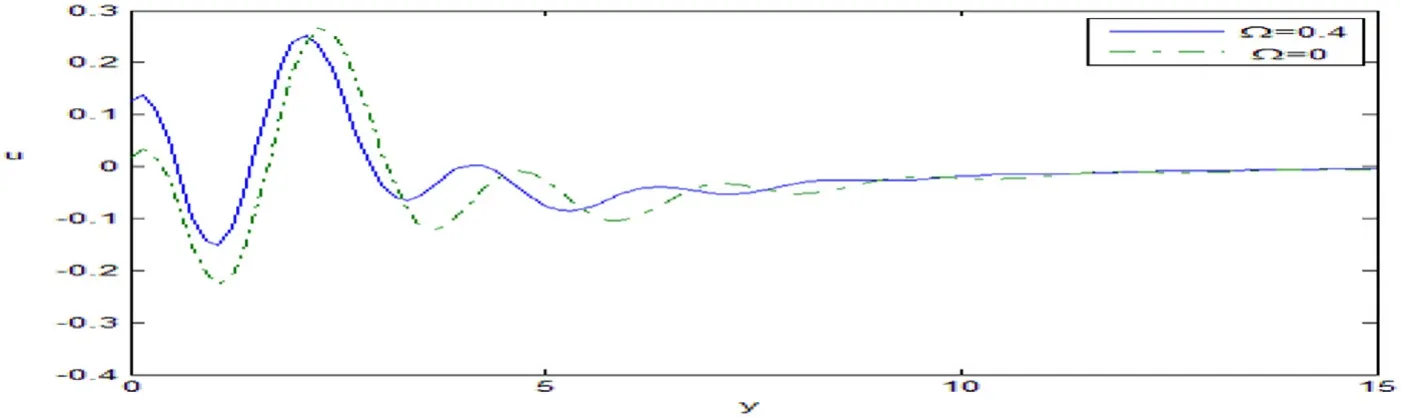
Fig.1.Variation of the displacement μ against y.

Fig.2.Variation of the microtemperatures vector w 1 against y.
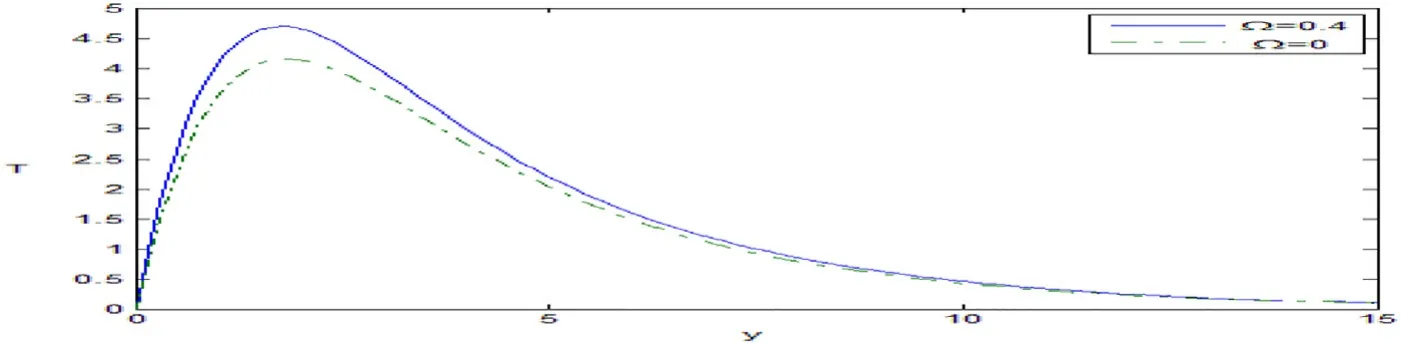
Fig.3.Variation of the temperature T against y.
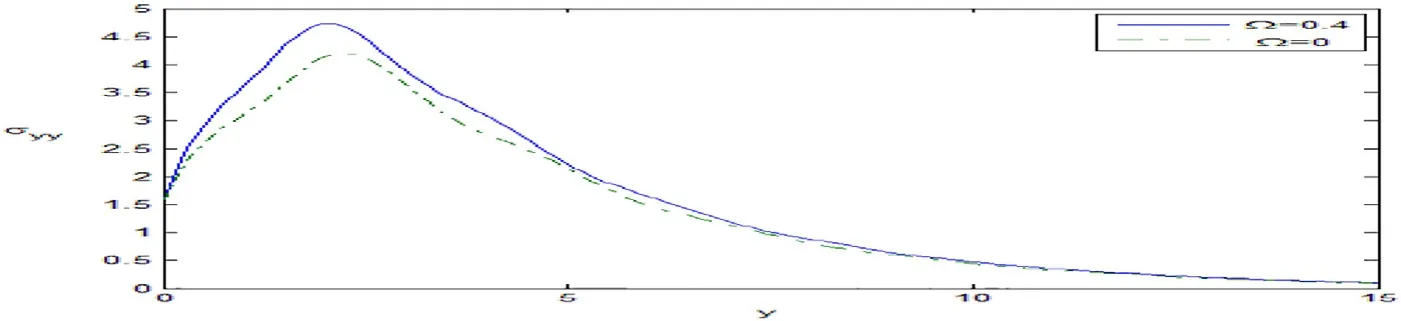
Fig.4.Variation of the stress σyy against y.
Fig.6 determines the variation of the first heat flux momentqxy,it is noticed thatqxydecreases in the ranges 0 ≤y≤0.3,0.7 ≤y≤1.9,3.1 ≤y≤4.2,5.3 ≤y≤6.5,7.5 ≤y≤8.7,9.7 ≤y≤11 and 12 ≤y≤15,while it increases in the intervals 0.3 ≤y≤0.7,1.9 ≤y≤3.1,4.2 ≤y≤5.3,6.5≤y≤7.5,8.7 ≤y≤9.7 and 11 ≤y≤12 with the increase of the rotation.
It can be deduced that the rotation has an effective role in the variation of all the physical quantities in the problem.
Fig.7 shows that the displacement componentuincreases for 0 ≤y≤15 with the increase of the gravity.Fig.8 clarifies the variation of the microtemperatures vectorw1,which increases fory>0 with the increase in the gravity.
It is clear that from Fig.9 the variation of the temperatureTincreases with the increase of the gravity for 0 ≤y≤15.Fig.10 depicts the variation of the normal stressσyywhich increases with the increase of the gravity for 0 ≤y≤15.
Fig.11 explains that the variation of the microrotation vectorφ3decreases in the ranges 0 ≤y≤1,2 ≤y≤3 and 4 ≤y≤15,while it increases in the ranges 1 ≤y≤2,and 3 ≤y≤4 with the increase of the gravity.

Fig.5.Variation of the microrotation vector φ3 against y.
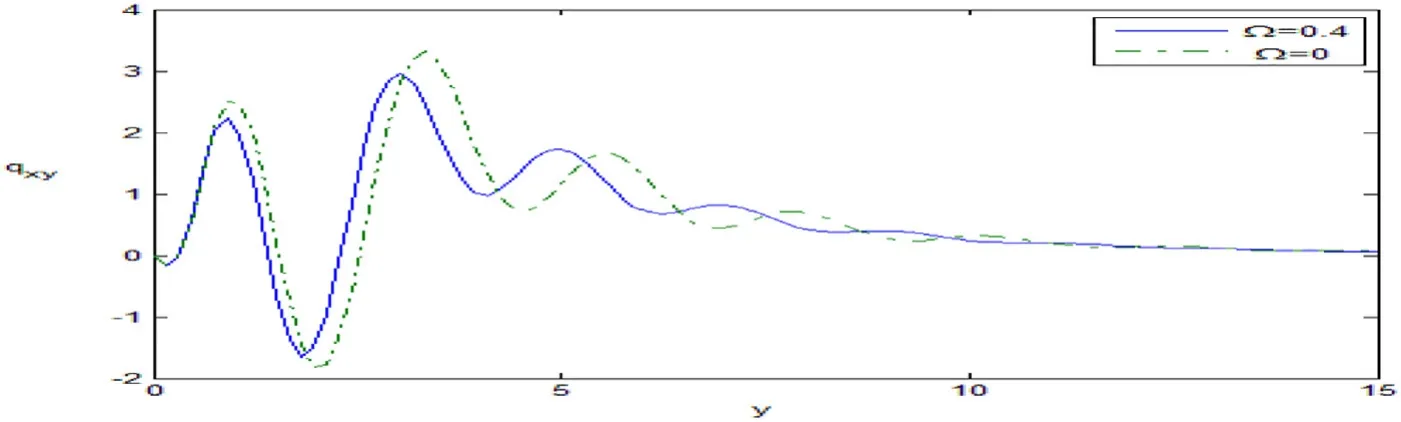
Fig.6.Variation of the first heat flux moment qxy against y.
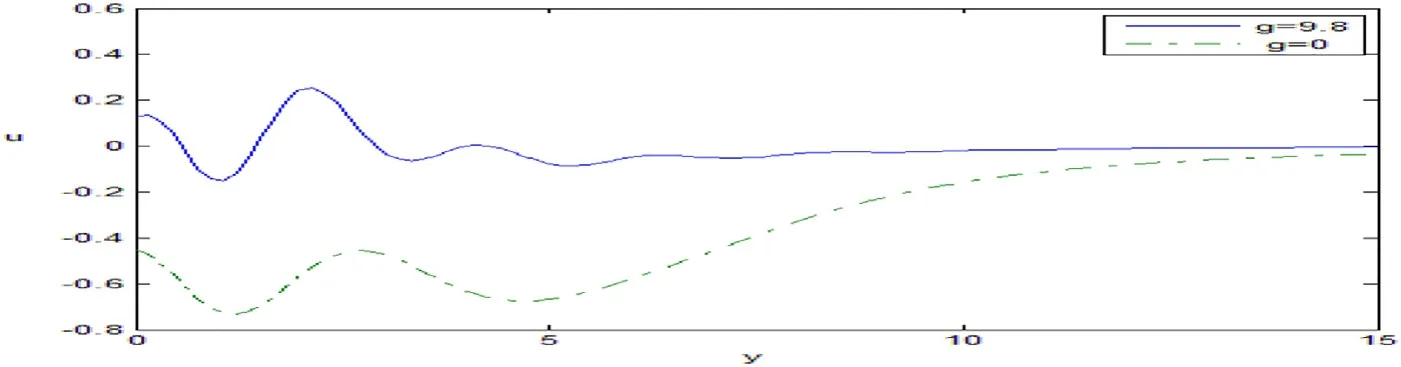
Fig.7.Variation of the displacement μ against y.
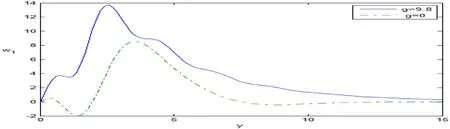
Fig.8.Variation of the microtemperatures vector w 1 against y.
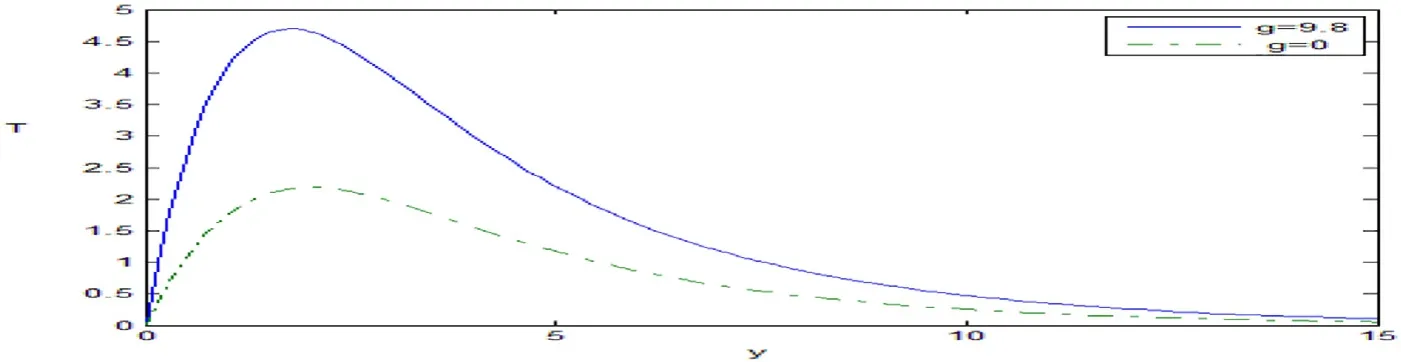
Fig.9.Variation of the temperature T against y.
Fig.12 states that the variation of the first heat flux momentqxy,which decreases in the ranges 0 ≤y≤0.5 and 1 ≤y≤2,while it increases in the ranges 0.5 ≤y≤1 and 2 ≤y≤15 with the increase of the gravity.The gravity has a significant role in the variation of the physical quantities in the problem.
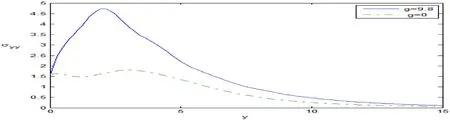
Fig.10.Variation of the stress σyy against y.
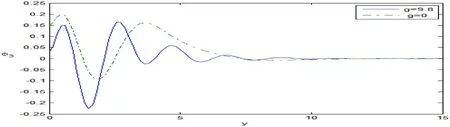
Fig.11.Variation of the microrotation vector φ3 against y.
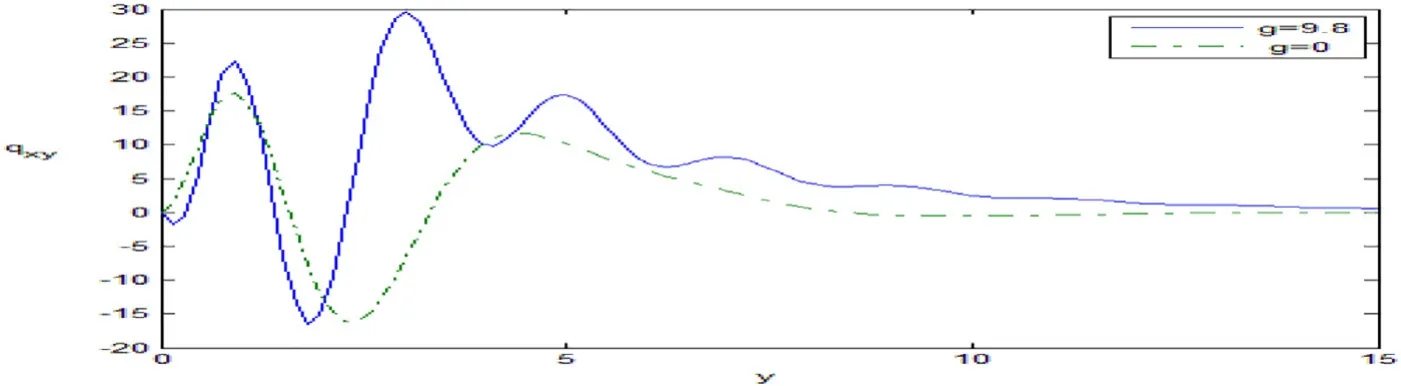
Fig.12.Variation of the first heat flux moment q xy against y.
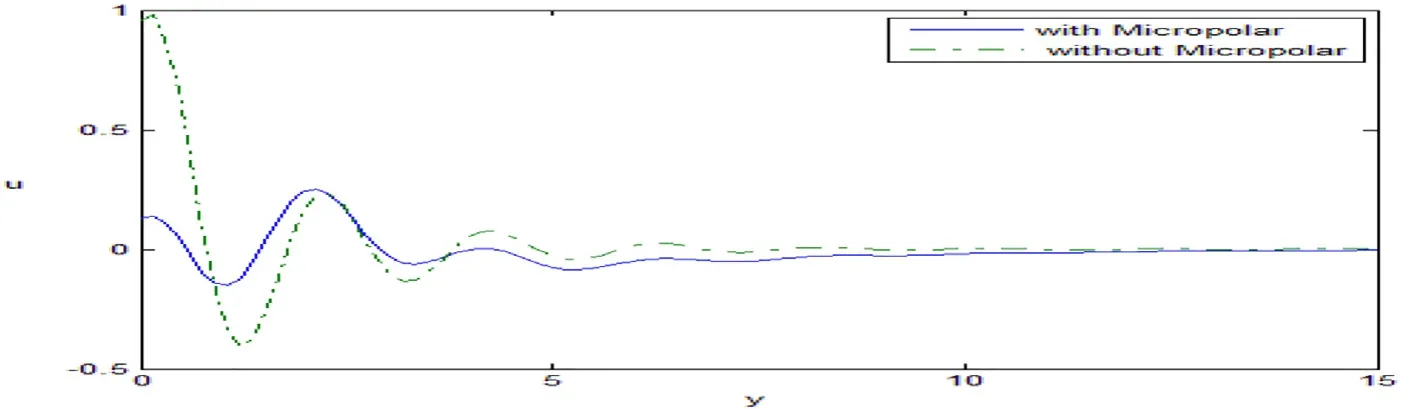
Fig.13.Variation of the displacement μ against y.
Fig.13 shows the variation of the displacement componentudecreases with the ranges 0 ≤y≤1,4 ≤y≤15 and increases in the range 1 ≤y≤4 with the increase of micropolarity of the medium.It is clear that from Fig.14 the variation of the temperatureTincreases with the increase of micropolar parameters in 0 ≤y≤15.
Fig.15 shows the variation of the tangential stressσxy,which increases in the ranges 0 ≤y≤1,2.1 ≤y≤2.7,4 ≤y≤5,5.5 ≤y≤15 while it decreases in the ranges 1 ≤y≤2.1,2.7 ≤y≤4,and 5 ≤y≤5.5 with the increase of the micropolar parameters.It is clear that all the functions are continuous and all the curves converge to zero.The micropolar has an important role in the variation of all the physical quantities in the problem.
The 3-D Figs.16-18,whereΩ=0.4 rad/s andg=9.8 m/s2with presence of the micropolar att=0.5 s;show that the behavior ofu,,φ3,andσxy,which propagate like waves and finally converge to their initial states.
5.Conclusions
The results presented in this article may be serving as benchmarks for many branches for the future technology.The microtemperatures theory is a very useful theory in the field of geophysics and earthquake engineering and seismologist working in the field of mining tremors and drilling into the earth’s crust.It is found that the rotation and the gravity have great roles in the variation of the considered physical quantities as micropolar presence.The value of all physical quantities converges to zero with increasing the distanceyand all the functions are continuous.
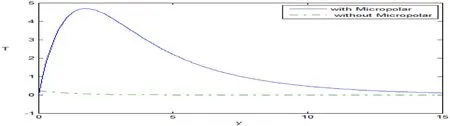
Fig.14.Variation of the temperature T against y.
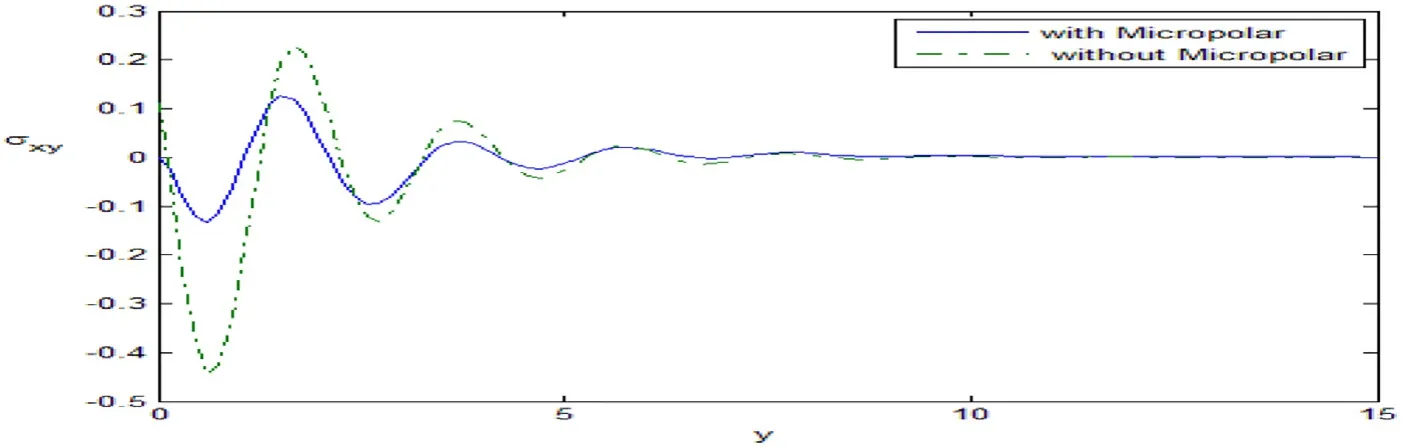
Fig.15.Variation of the stress σxy against y.

Fig.16.the 3-D curve of the displacement μ versus the distances.
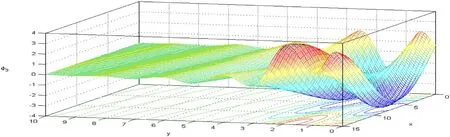
Fig.17.the 3-D curve of the microrotation vector φ3 versus the distances.

Fig.18.the 3-D curve of the stress σxy versus the distances.
Appendix
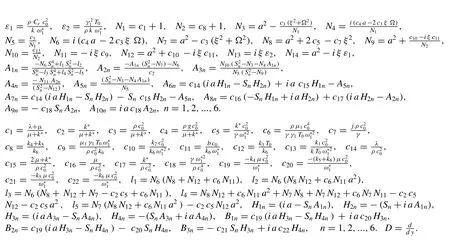
 Journal of Ocean Engineering and Science2020年3期
Journal of Ocean Engineering and Science2020年3期
- Journal of Ocean Engineering and Science的其它文章
- Distortion performance of underwater acoustic mobile networks
- A modeling method for vibration analysis of cracked beam with arbitrary boundary condition
- Ship speed power performance under relative wind profiles in relation to sensor fault detection
- Role of mesoscale eddies on atmospheric convection during summer monsoon season over the Bay of Bengal:A case study
- Effect of rotation on the surface wave propagation in magneto-thermoelastic materials with voids
- Iterative algorithm for parabolic and hyperbolic PDEs with nonlocal boundary conditions
