Tao Wen,Sai Ying,FengXi Zhou

1. Chongqing Engineering Research Center of Building Health Monitoring and Disaster Prevention in Full-Life-Cycle,Yangtze Normal University,Chongqing,408100,China

2.Gansu Academy of Sciences,Lanzhou,Gansu 730000,China

3.School of Civil Engineering,Lanzhou University of Technology,Lanzhou,Gansu 730050,China

ABSTRACT Based on salt-frost heave tests of sulfate saline soil under repeated freeze-thaw cycles, this paper discusses the mechanism of the salt-frost heave under long-term freeze-thaw cycles.The results show that the salt-frost heave can be restricted considerably by loads,and there is a critical load for the salt-frost heave cumulative effect.Under this load,peak values of salt-frost heave approach a constant,and the residual values become 0.There is no longer structure heave or cumulative effect of saline soil exposed to freeze-thaw cycles under the critical load.Taking cumulative effect into account in calculations of salt-frost heave,a salt-frost heave model under freeze-thaw cycles is developed.

Keywords:sulfate saline soil;freeze-thaw cycles;load;salt-frost heave

1 Introduction

Sulfate saline soil is one of the main saline soil types in the northwest cold and drought region of China. Saline soil exposed to seasonal freeze-thaw conditions exhibits great potential for salt-frost heave,which can cause engineering damages,such as bumping, cracking, and strength decrease of foundations(Wanget al., 2003; Chenget al., 2007; Wuet al.,2010). These problems can affect numerous infrastructure constructions such as highways, airports,low buildings, and oil and gas pipelines in western China.

It is generally recognized that crystal growth of salts and ice in the sulfate saline soil causes salt-frost heave when temperatures drop below the freezing point of saline soil. Recently, numerous studies have focused on the mechanism of salt and ice crystal formation and growth in porous materials (Scherer,1999; Steiger, 2005; Espinosaet al., 2008; Wanet al., 2017), with dynamics of crystallization pressure evolving in porous materials fully discussed. Based on the kinetics of salt crystallization/dissolution and water freezing/ice thawing and microstructure-Poromechanical approach, Koniorczyk (2010, 2012, 2015,2018) proposed mathematical models of chemo-hydro-thermo-mechanical behavior of porous building materials.Also, engineering the methods of quantitative analysis of salt expansion and frost heave of saline soil is badly needed. Song and Chen (2006) analyzed computational methods for expansion of saline soil with an artificial neural network and established formulae to describe the salt expansion properties of saline soil as a function of water content, NaCl concentration, Na2SO4concentration, initial dry density,and overburden pressure of saline soil. Niu and Gao(2008, 2015) gave a formula for calculation of salt expansion under a single cooling condition from the view of phase transition of water and salt.They found that there was a parabolic relationship between the concentration of Na2SO4solution and the upper limit of sensitive temperature of salt expansion. Xiao (2017)proposed a method for computation of salt-frost heave based on porous media mechanics, considering that the salt-frost heave of soil results from the coupling effect of many factors, such as the phase change effect and thermal deformations. Liet al.(2016) built a method for calculating the volumetric change rate of the Na2SO4+H2O system during the cooling process. In the calculation procedure, the content of phases is determined according to the equilibrium concentration of phases in the system of Na2SO4+H2O, and the volume of the phases was added to calculate the volumetric change rate of the Na2SO4+H2O system.Our research team (Yueet al.,2017)experimentally obtained the relationship between expansion stress and volume expansion strain of sulfate saline sandy soil, and established an expression for calculating the critical overlying load when the compression and salt-frost expansion of foundations become equal. However, for the most part, the existing computing formulae were based on salt-frost heave due to phase transition of salt and water without considering structure heave due to the change of soil structure, which has a great effect on long-term salt-frost heave.

This paper reports a calculating method for determining salt-frost heave of sulfate saline soil under long-term freeze-thaw cycles. The method is based on the relationship between dry density and salt-frost heave ratio and considers the influence of changes of soil structure through salt-frost heave experiments with long-term freeze-thaw cycles under load using a self-developed instrument. This work aims to provide scientific guidance for the evaluation and prevention of long-term salt-frost heave hazards of sulfate saline soil foundations in seasonal frozen soil areas of western China.

2 Description of experiments

2.1 Material properties

The experimental soil was clay silt loess from Lanzhou district, which is one of the main seasonal frozen soil areas of western China.The soil was desalinized by pure water twice to ensure accuracy of the salt content of the prepared samples. The physical properties and soluble salt contents of the desalinized soil are given in Tables 1 and 2.The effective components content of sodium sulfate used in this experiment is greater than 99%.

Table 1 Physical properties of soil

Table 2 Contents of soluble salts in soil

2.2 Sample preparation

The desalinized soil was dried to a moisture content of 9.3% and then mixed uniformly with prepared sodium sulfate solution,after that the soil was sealed in storage bags to prevent evaporation for 24 hours. The moisture content was 17.3% and the salt content was 3%.Then the cylindrical test sample with 15 cm in diameter and 30 cm in height was made in a segmented container from the prepared soil using the hierarchical compaction method. The compaction of the test sample was divided into five layers,and each layer had the same dry density of 1.697 g/cm3, corresponding to a compaction degree of 96% (the moisture content of 17.3% and maximum dry density of 1.768 g/cm3were obtained by the light compaction test).

2.3 Freeze-thaw procedure

Salt-frost heave was investigated experimentally by means of a self-constructed device which can measure strain difference in different temperature, moisture and load conditions.

The experimental device is presented in Figure 1.The experiment soil was compacted into a hollow segmented stainless-steel container. Working liquid(alcohol) was circulated inside the cooling bath to control the temperature(-20 °C to 100 °C)of the sample. Soil temperatures were recorded during freezethaw cycles in the center of samples using PT100 temperature sensors with accuracy of ±0.1 °C and resolution of 0.1 °C.A freeze-thaw cycle contains a series of temperature intervals of 15 to 6 °C, 6 to 0 °C, 0 to-5 °C, -5 to -10 °C, and -10 to 15 °C. The vertical deformations were recorded during testing using digital dial indicators (accuracy of ±0.02 mm), which were fixed on top of the test sample. When the deformation change of the test sample in an hour was less than 0.1 mm, the temperature would enter into the next interval. To record the changes of density of test samples in different depths during testing, density tests were carried out at 0, 8, 16, and 24 cm in depths after 0, 5, 8, and 11 cycles of freeze-thaw. Soil samples for the density tests were 2 cm in diameter and 3 cm in height, and the sampling device is presented in Figure 2.When the temperature was heated to 15°C,holes 2.4 cm in diameter were dug to 2 cm beyond the sampling depths, and then the soil samples were carried out by the sampling device. The sampling holes were uniformly distributed in the circumference of which the radius was 4 cm and the center of circle is the center of the test sample, and the sampling holes were backfilled by the prepared soil after sampling.To study the effect of different loads on the deformation of samples exposed to freeze-thaw cycles,different loads of 0, 15, 30, 60, and 90 kPa were imposed on the samples using a lever during the freeze-thaw cycles.

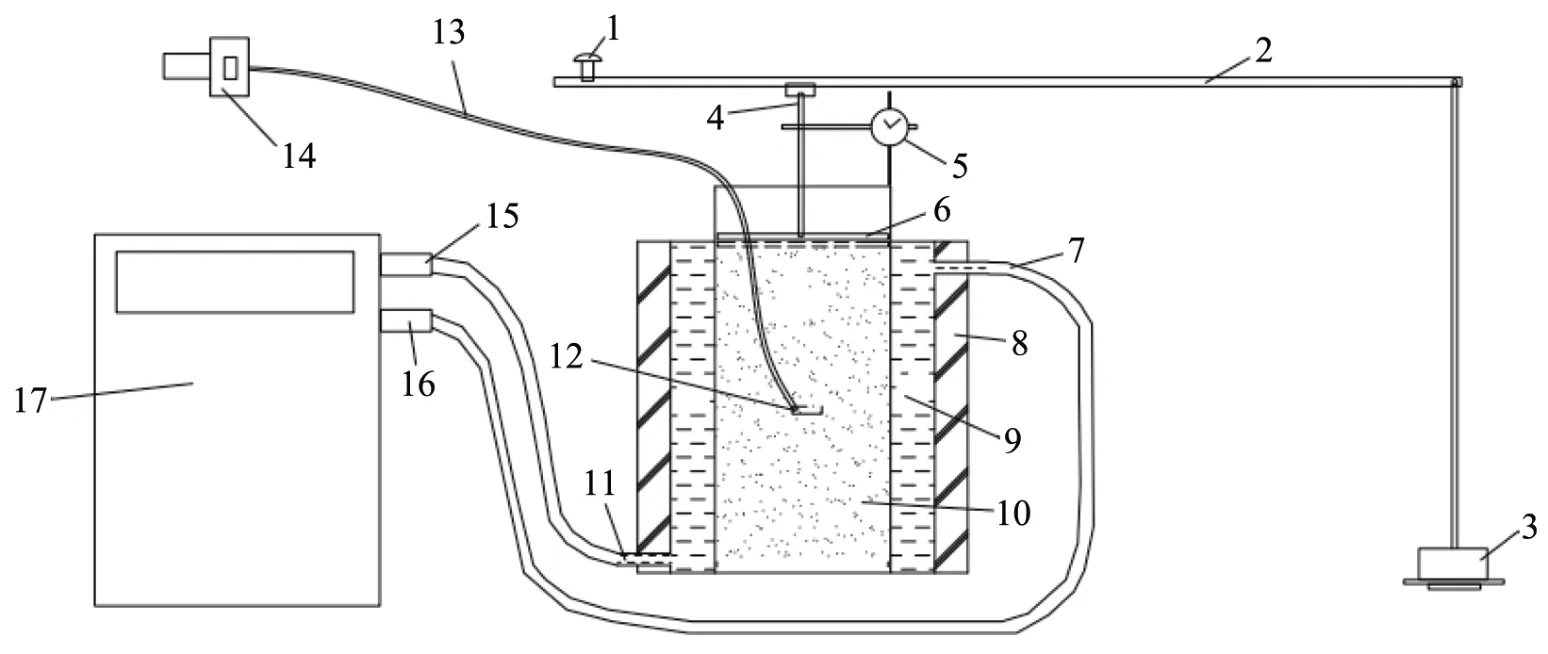
Figure 1 Structural diagram of multifunctional salt-frost heave apparatus(1.Nut for leveling of lever;2.Lever for load;3.Weight;4.Dowel steel;5.LVDT;6.Loaded plate;7.Refrigerating fluid outlet of temperature-control box;8.Thermal insulation layer;9.Refrigerating fluid;10.Sample;11.Refrigerating fluid inlet of temperature-control box;12.Temperature sensor;13.Temperature sensor cable;14.Temperature acquisition device;15.Refrigerating fluid outlet of low temperature bath;16.Refrigerating fluid inlet of low temperature bath;17.Low temperature bath)

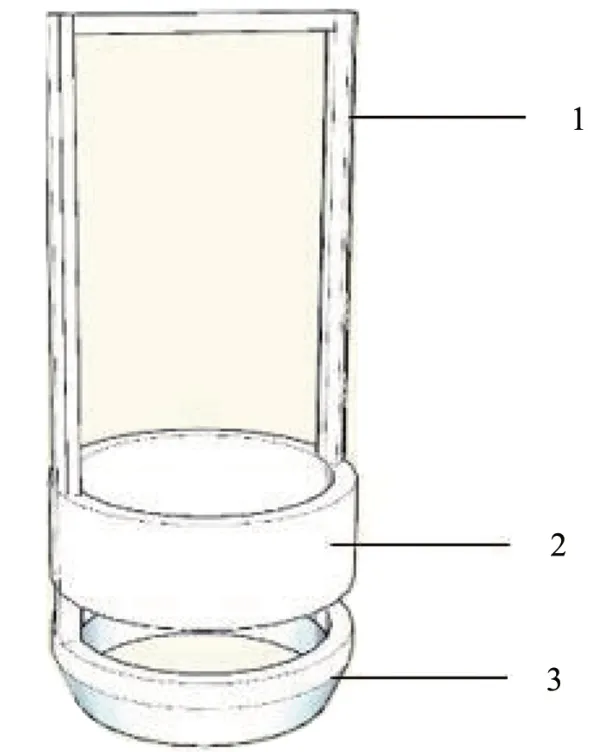
Figure 2 The sketch map for the sampling device(1.Long handle;2.Cutting ring;3.Removable cutting ring)

3 Experimental results

3.1 Salt-frost heave mechanism of sulfate saline soil due to long-term freeze-thaw cycles

Typical results are presented in Figure 3, where the salt-frost heaves of different cycles are plotted versus time for various test stages.The peak value of the salt-frost heave is the maximum of the curve in Figure 3, and the residual value is the value at the endpoint of the curve. There was a linearly increasing relationship between peak values (residual values) of salt-frost heaves and the number of freeze-thaw cycles (Figure 4).The results show a similar pattern to published data (Chuet al., 1998), indicating that salt-frost heaves will increase with increasing freeze-thaw cycles in sulfate saline soil. In addition, there was a high in-crease of peak values and residual values of salt-frost heaves, and the increment were almost the same. For example, the peak value of salt-frost heave increased 13.53 times from first cycle to 11thcycle and the residual value correspondingly increased 13.24 times.

Figure 3 The salt-frost heaves in freezing-thawing cycles

To explore the mechanism of salt-frost heave of sulfate saline soil exposed to freeze-thaw cycles, dry densities in different depths of test sample were measured(Figures 5 and 6).Figure 5 shows that dry densities at different sampling depths decreased with increasing number of freeze-thaw cycles, and the value of reduction of dry density decreased with increasing depth,which is a hysteresis phenomenon.For example,the dry density at 0 cm depth decreased from 1.696 to 1.503 g/cm3after 11 cycles, of which the value of reduction is 0.193 g/cm3. In contrast, dry density at 24 cm depth decreased from 1.699 to 1.682 g/cm3, of which the value of reduction is 0.017 g/cm3. Moreover, only after five cycles the dry density at 0 cm depth decreased from 1.696 to 1.682 g/cm3, but for the dry density at 8 cm depth, 8 cycles were needed.Figure 5b shows that with an increasing number of cycles,dry density at 0 cm depth initially decreased rapidly and then slowed, finally became a constant. The relationship between dry density and the number of cycles is presented in Equation(1).

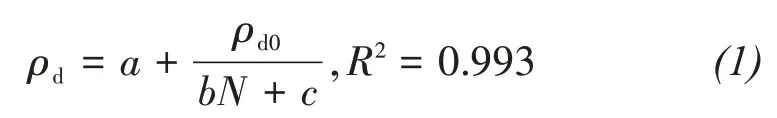
whereρd0(g/cm3) andρd(g/cm3) are initial dry density and dry density exposed toNcycles of freeze-thaw,respectively,a,bandcare fitting parameters.

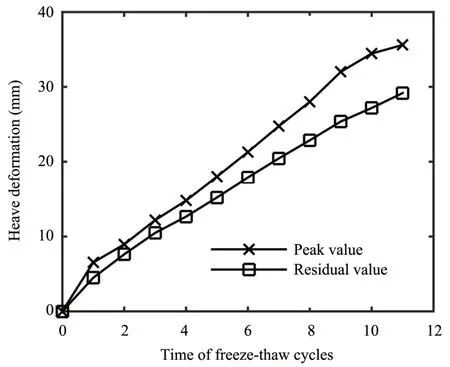
Figure 4 Relationships between frost-heaves and times of freeze-thaw cycles

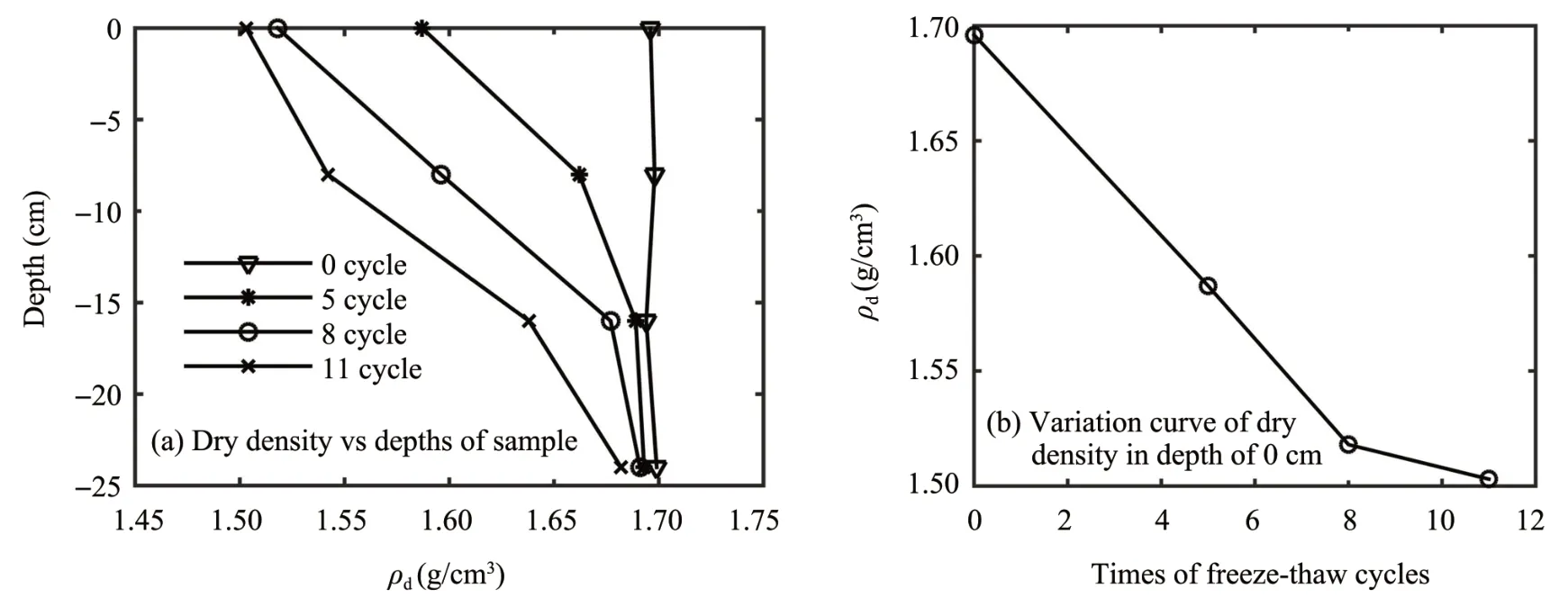
Figure 5 Variation curve of dry density with times of freeze-thaw cycles

The experimental results indicate that structure heave occurs when saline soil is exposed to freeze-thaw cycles. In the cooling process, the crystals of water and salt grow against the soil aggre-gates exerting high pressure, which induces the crushing of soil aggregates and the increasing of pores size, as a result salt-frost heave occurs. The crystals cohere to tiny soil particles,causing accumulation into large soil aggregates that contain soil and salt, and this process changes the size and arrangement of soil aggregates. In the heating process, due to the disappearance of crystals, the soil matrix lose the support of crystals and pore size decreases.Thus,soil aggregates cannot return to the initial state because of the existence of internal friction, cohesive force, matric suction and undissolved salt crystals,and it is easy to form the macropore structure as presented in Figure 6. The unrecoverable heave is the structure heave induced by changes of the size and arrangement of soil aggregates under freeze-thaw cycles.Also,the macropore structure will be easily damaged by loads, and the structure heave can be considerably restricted by loading. The restraint from the barrel wall and the overlying soil layer along the height of the sample is non-uniform. The deeper the layer is, the stronger the restraint becomes, we can observe that dry density decreases more slowly at greater depths(Figure 7).

Figure 6 The schematic diagram of the formation of macropore structure

Figure 7 Picture of sample in different depths after 8 freeze-thaw cycles

3.2 Relationship between freeze-thaw cycles and salt-frost heave deformation under different loads

In Figure 8, the relationship between peak (residual) values of salt-frost heave and the number of freeze-thaw cycles are plotted which are different under different loads. When the load is 0 kPa, salt-frost heave increases rapidly and linearly with an increasing number of freeze-thaw cycles.When load increases to 15-60 kPa, the salt-frost heave deformation increases exponentially with the increasing number of freeze-thaw cycles, and the growth becomes slower than that under the 0 kPa load. When load is 90 kPa,salt-frost heave decreases exponentially with an increasing number of freeze-thaw cycles. The relationship between freeze-thaw cycles and salt-frost heave is obtained as Equation(2)and the corresponding parameters are listed in Table 3.

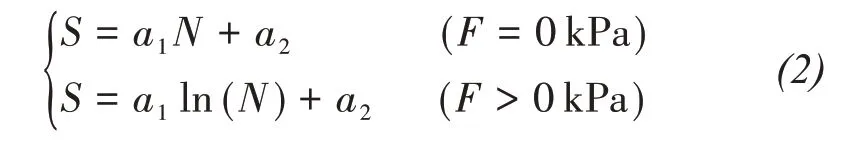
whereSare peak (residual) salt-frost heave deformations exposed toNcycles of freeze-thaw.

Equation(2)and Table 3 show that the peak and residual values of salt-frost heave have a consistent relationship with the number of freeze-thaw cycles.

3.3 Relationship between loads and salt-frost heave after different number of freeze-thaw cycles

In Figure 9, it is shown that peak (residual) values of salt-frost heave decreased rapidly and then became slower with an increase of loads, and all the curves intersect at one point, indicating that the values of salt-frost heave approached a constant when load became 70-75 kPa.At this point, peak salt-frost heave is about 2.0 mm,and the residual value is about 0 mm.

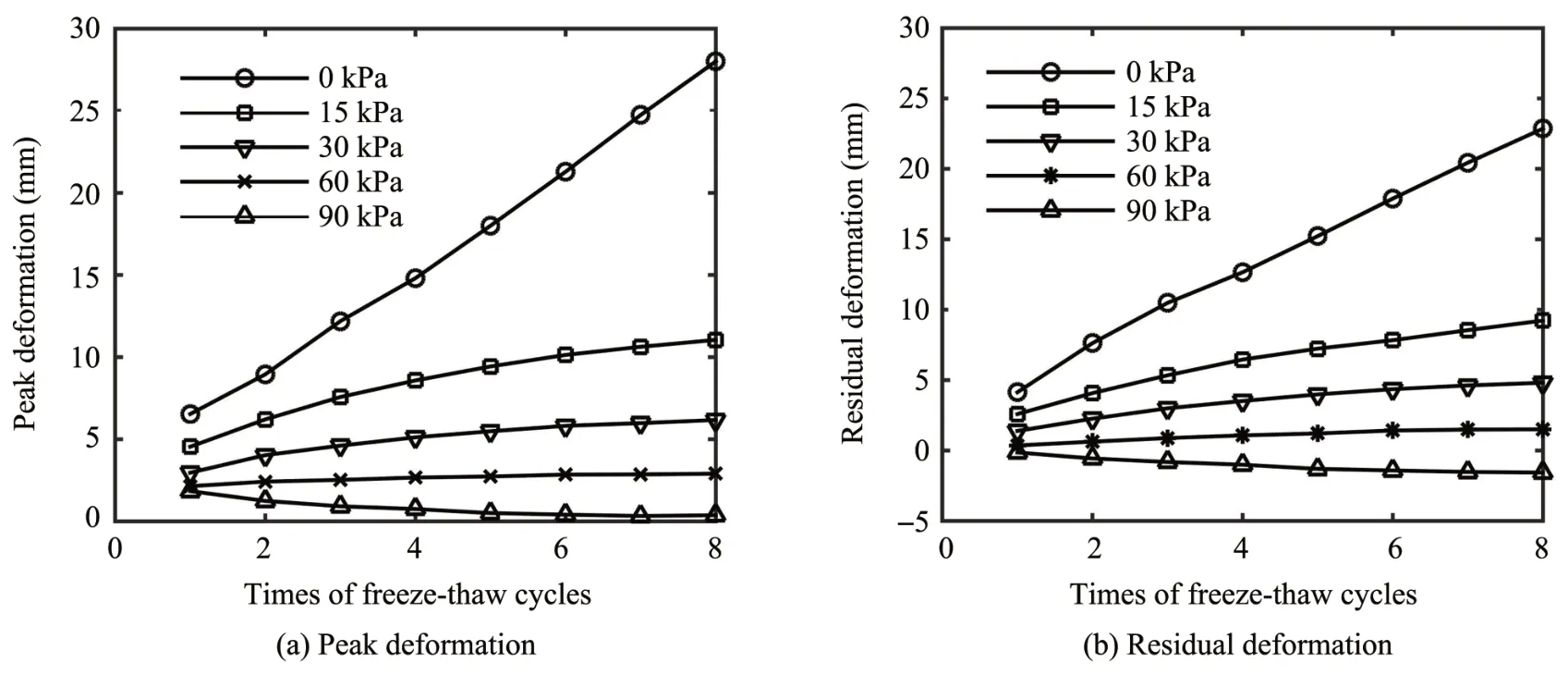
Figure 8 Relationships between peak(residual)values of salt-frost heave and the number of freeze-thaw cycles under different loads

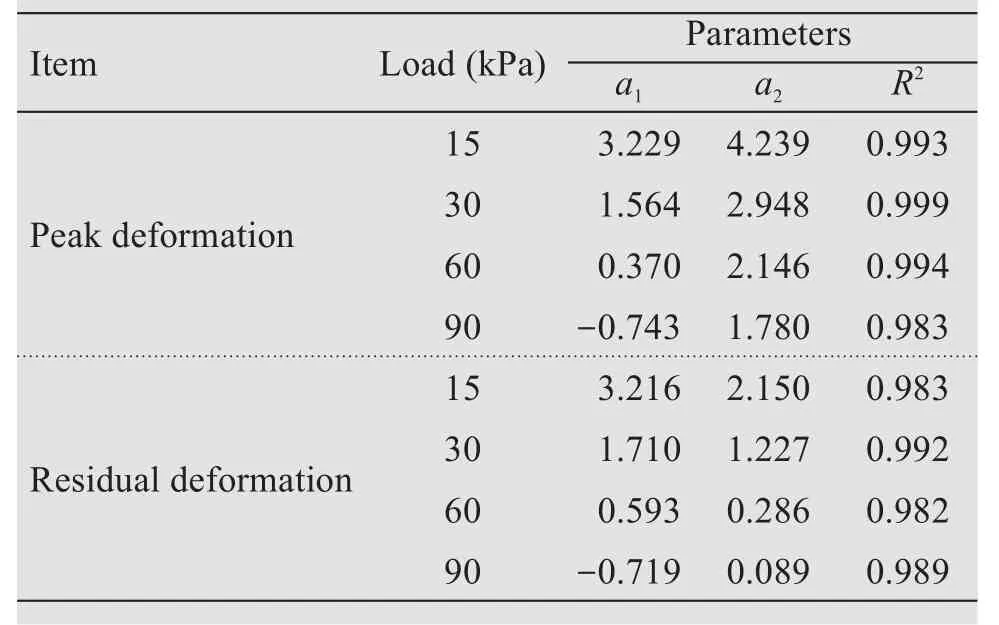
Table 3 Parameters of Equation(2)

Equation(3)presents the relationship between peak (residual) salt-frost heave deformations and loads which is based on the fitting curves in Figure 8 and the corresponding parameters are listed in Table 4.

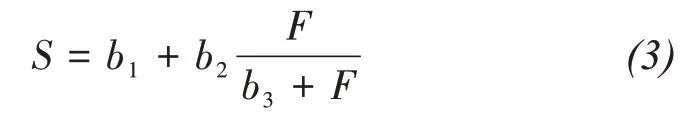
whereS(mm) is the peak (residual) salt-frost heaves andF(kPa)are overlying loads.

The salt-frost heave consists of the volume of phase transition of crystals and the structure heave,and the loads have little influence on the volume of phase transition of crystals phase transition. However, structure heave can be considerably restricted by the loads.Our experiment results indicate that structure heave can be restricted to 0 when load increased to 70-75 kPa.As a result, the curves in Figure 10 intersect at one point,and at this point structure heave is restricted to 0 and the increase of salt-frost heave is only subjected to the volume of phase transition of crystals and is independent of the number of freeze-thaw cycles.

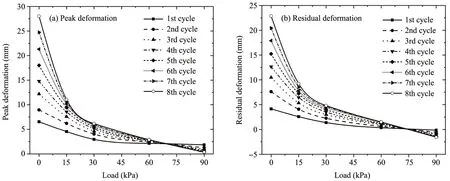
Figure 9 Relationships between peak(residual)values of salt-frost heave and loads under different times of freeze-thaw cycles

These results show that there is a critical load that can completely restrict the structure heave to 0 of sulfate saline soil exposed to long-term freeze-thaw cycles.Under this load,salt-frost heave is only subjected to phase transition of crystals, and is independent of the number of freeze-thaw cycles. The peak values and residual values of salt-frost heaves approach a constant respectively and the cumulative effect of salt-frost heave under freeze-thaw cycles disappears when residual values became 0,and we called the corresponding load the "critical load of salt-frost heave cumulative effect". The magnitude of the load should be considered when calculating salt-frost heave under long-term freeze-thaw cycles. Therefore, when load is less than the critical load of salt-frost heave cumulative effect, structure heave should be considered.When load is more than the critical load of salt-frost heave cumulative effect, structure heave can be neglected, and salt-frost heave can be calculated for a single decrease of the temperature condition.

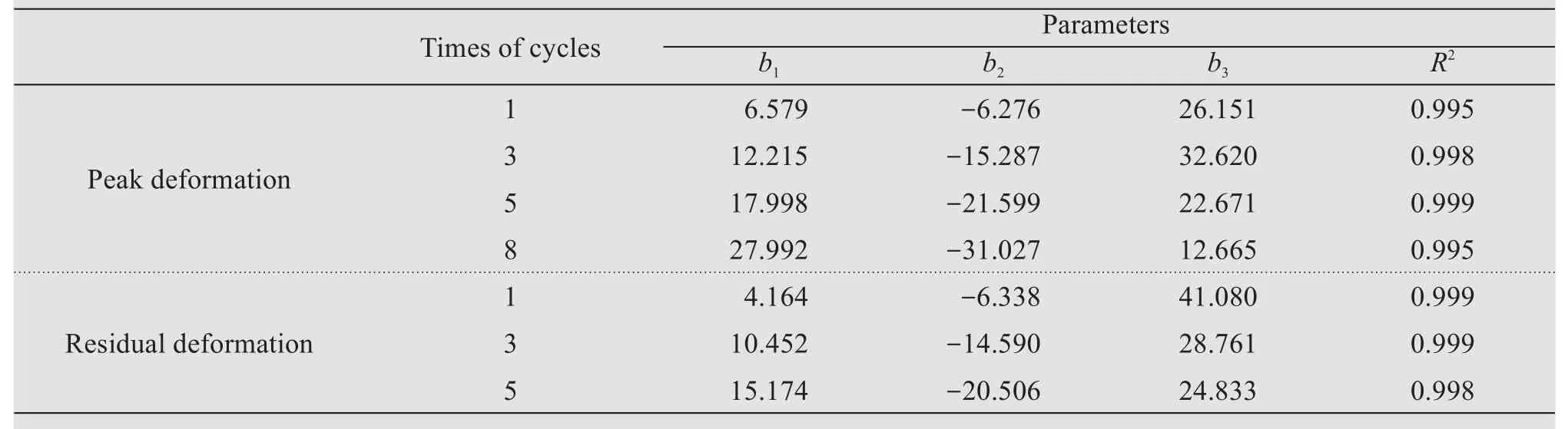
Table 4 Parameters in Equation(3)

Figure 10 Soil structural features of top surface of test sample under different loads exposed to eight freeze-thaw cycles.(a)The sample under load of 0 kPa;(b)The sample under load of 15 kPa;(c)The sample under load of 30 kPa;(d)The sample under load of 60 kPa;(e)The sample under load of 90 kPa

4 Calculation model for salt-frost heave of sulfate saline soil exposed to long-term freeze-thaw cycles

4.1 Application conditions

The following application conditions of calculation model for salt-frost heave of sulfate saline soil exposed to long-term freeze-thaw cycles should be followed to ensure a precise result:

(1)The soil should be saline loess.

(2) There should be no water supply during freeze-thaw cycles, and water content of soil should stay within the optimum water content(wop)±2%.

(3)The cooling rate should be less than 1.25°C/h.

(4)The sulfate saline soil foundation is considered to be homogeneous isotropic elastic semi-space, and salt-frost heave is completely sidewise confined which can only produce vertical deformation.

(5) Soil is divided into layers based on salt content, water content, and soil properties, and the soil property of each layer is the same.

The conditions mentioned above match with engineering conditions of residual sulfate saline soil in the northwest seasonal frozen region of China. Related studies (Shiet al., 1994; Dinget al., 2008) have indicated that the maximum value of salt-frost heave occurs when the water content is nearwop,therefore,it is reasonable to evaluate hazards of salt-frost heave using the value of salt-frost heave calculated underwop.

4.2 Calculation of the critical load of the salt-frost heave cumulative effect

The aforementioned experiment results (Figure 8b)show that under critical load of salt-frost heave cumulative effect, the peak (residual) value of salt-frost heave was 0, which was independent of the number of freeze-thaw cycles.Therefore,the computing equation for critical load of salt-frost heave cumulative effect based on Equation(3)withS=0 was obtained as follows:

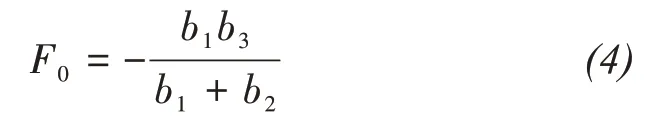
whereF0are critical loads for salt-frost heave cumulative effect; andb1,b2andb3are parameters in Equation(3).

In engineering, overlying loadsFin different layer depths and the critical loads of salt-frost heave cumulative effectF0can be used to distinguish whether there is a cumulative effect of sulfate saline soil exposed to freeze-thaw cycles. IfF＜F0, it indicates that there is cumulative effect in the soil layer, and ifF≥F0,there is no cumulative effect.

4.3 Calculation of the critical depth of the salt-frost heave cumulative effect

The definition of critical depth of salt-frost heave cumulative effect is the distance between a critical layer and the bottom of the foundation when the load of the critical layer equals the critical load of the salt-frost heave cumulative effect. Here, if the additional pressure at foundation bottom isp, we can calculate the vertical pressure at depthzfrom the foundation bottom with Equation(5):

whereσz(kPa)is the vertical total stress in depthzfrom foundation bottom,σc(kPa) is the sum of self-weight stress of layers from the foundation bottom tozdepth going downwards from the foundation bottom, andis the weight density of each soil layer in the calculation,zi(m) is the thickness of each soil layer,nis the number of soil layers in calculation;αis the vertical additional stress coefficient, andp(kPa) is the additional pressure at the foundation bottom.

Based on the definition of critical depth of saltfrost heave cumulative effect, the expression of critical depth of salt-frost heave cumulative effect can be obtained as Equation(6)if we substituteσz=F0into Equations(3)and(4):

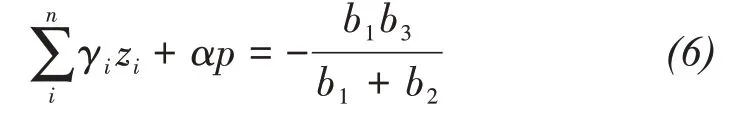
Now we can use the equations to distinguish whether the soil has a salt-frost heave cumulative effect. As the first step, we used Equation(6)to determine the critical depth of the salt-frost heave cumulative effectzi,j, and then divide the soil into layers along demarcation line ofzi,j. Next, we can use Equation(5)to calculateσz. Ifσz＜F0, the soil layer has the salt-frost heave cumulative effect, whereas ifσz≥F0,the soil layer has no salt-frost heave cumulative effect(Figure 11).

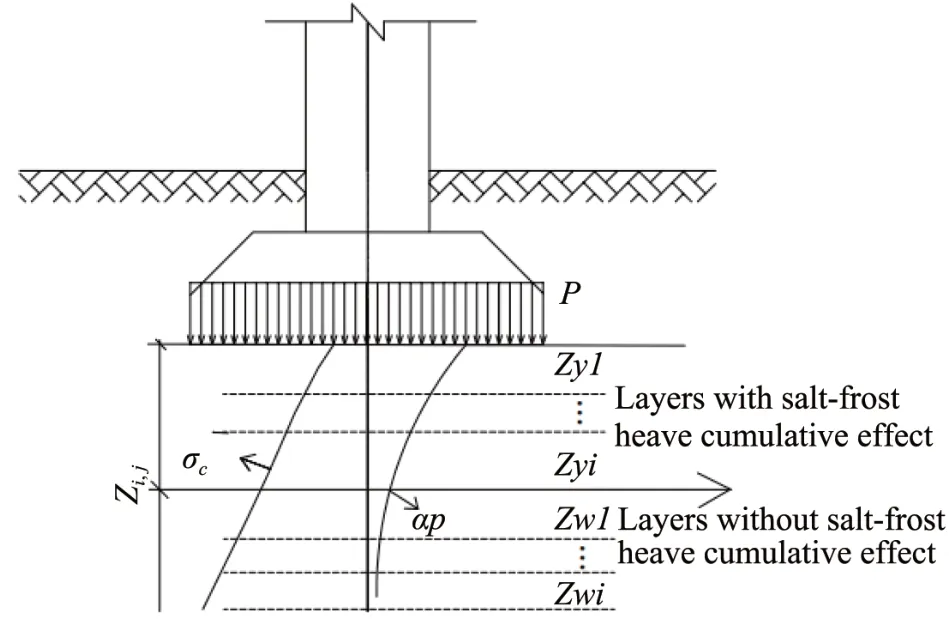
Figure 11 Schematic diagram of discriminant of cumulative effect of salt-frost heave deformation of foundation soil

4.4 Calculation of salt-frost heave

In Figures 7 and 8, it is shown that the change of the peak value and the residual value of salt-frost heave are the same, and the peak value of salt-frost heave is larger, therefore in this paper, the peak value of salt-frost heave is treated as the value of salt-frost heave. Based on Equation(6), the value of salt-frost heave is divided into two parts: the salt-frost heave with cumulative effect and the salt-frost heave without cumulative effect.

(1) Calculation of the value of salt-frost heave with cumulative effect

The relation of peak value of salt-frost heave and the number of freeze- thaw cycles is obtained by Equation(3)and the experiment, and can be expressed as Equation(7):

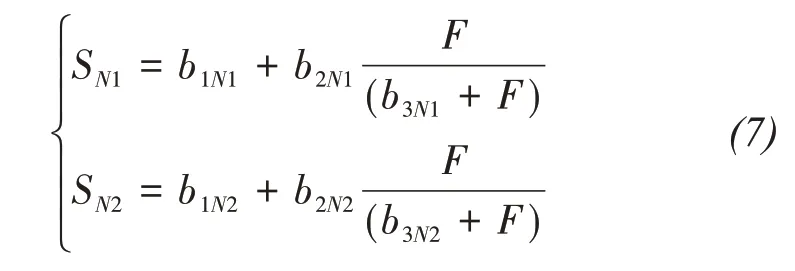
whereSN1andSN2are peak values of salt-frost heave exposed toN1andN2cycles of freeze-thaw,F(kPa) is the average value of vertical stress in top and bottom of the soil layer.

Coefficientsα1andα2in Equation(2)can be obtained by Equations(2)and(7).

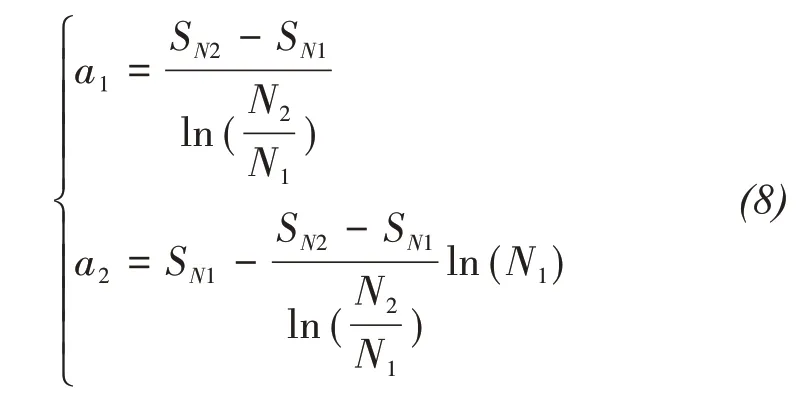
We obtain the peak values of salt-frost heave from Equations(2),(3),(7)and(8):

WhenSin Equation(9)is divided by the height of test sample we obtain the salt-frost heave ratio for the convenience of use as follows:

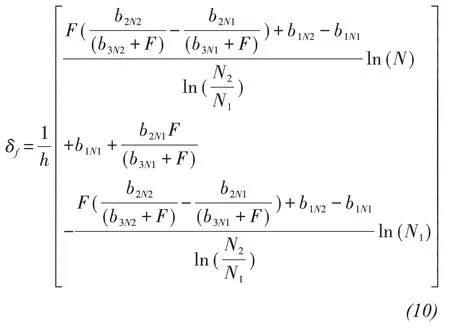
Soil layers can be divided according to the salt content and soil properties and then salt-frost heave with cumulative effect is obtained from Equation(10)as follows:

whereSy(m) is salt-frost heave with cumulative effect,δfiis salt-frost heave ratio with cumulative effect of theith soil layer, when calculatingδfiandZiy(m) is the thickness of the soil with salt-frost heave cumulative effect.

Equation(11)is convenient for engineering applications because the three parameters required can be obtained by a freeze-thaw experiment within two cycles.

(2) Calculation of the value of salt-frost heave without cumulative effect

Under different loads and freeze-thaw cycles, the value of salt-frost heave without cumulative effect depends on the phase transition of salt and water in soil and is independent of the number of freeze-thaw cycles. Therefore, based on the phase transition method and considering salt heave and frost heave process,the salt-frost heave ratio is given by Niu and Gao(2015):

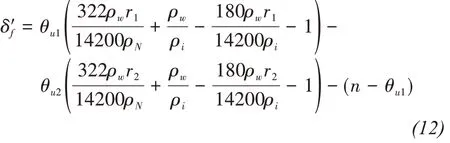
whereθu1is the volumetric water content of unfrozen water before cooling begins,θu2is the volumetric water content of unfrozen water after cooling is complete,ρw(g/cm3) is the density of water,ρi(g/cm3) is the density of ice,ρv(g/cm3) is the density of mirabilite,r1(mol/L) is the solubility of sodium sulfate before cooling begins,r2(mol/L) is the solubility of sodium sulfate after cooling complete,is salt-frost heave without cumulative effect, andnis the initial void ratio of soil before cooling begins.

The soil without salt-frost heave cumulative effect was divided into layers, according to salt content and soil properties, and then a derivation of Equation(12)for salt-frost heave without cumulative effect was conducted as follows:

whereSwis the value of salt-frost heave without cumulative effect,is the salt-frost heave ratio without cumulative effect of theith soil layer, andZiwis the thickness of the soil without the salt-frost heave cumulative effect.

(3) Computation of the value of salt-frost heave of saline soil foundation

The sum of Equations(11)and(13)can be used to compute the value of salt-frost heave (Sz) of saline soil foundation under load and freeze-thaw cycle conditions:

4.5 Calculating examples

The peak deformations of sulfate saline soil exposed to freeze-thaw cycles under loads of 15 kPa and 30 kPa can be calculated by Equation(11), and the calculated values and test values are presented in Figure 12. Figure 12 shows that the maximum difference between calculated values and test values under loads of 15 kPa is 7.13% at the 2nd freeze-thaw cycle, and the minimum difference is 0.01%. Under loads of 30 kPa, the maximum difference between calculated values and test values is 8.62% at the 1st freeze-thaw cycle, and the minimum difference is 1.39%. The comparison of calculated values and test values indicates that calculated results are very close to the test values, therefore the calculating model can be used for the predict of the salt-frost heave of sulfate saline soil exposed to freeze-thaw cycles in the northwestern cold and drought region of China.

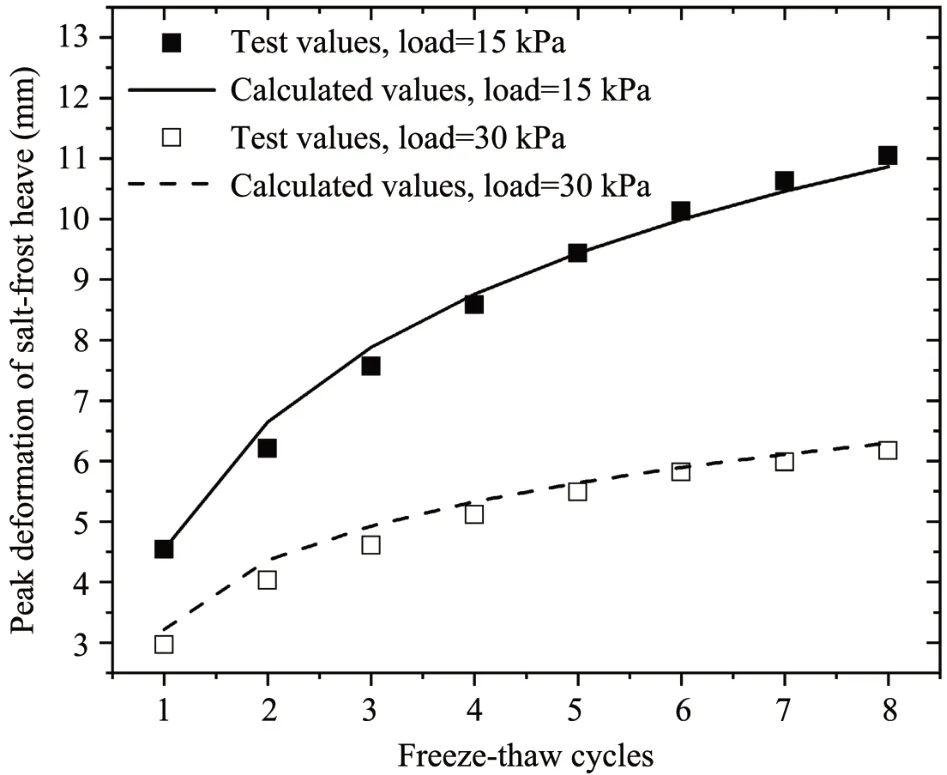
Figure 12 Comparison between calculated and test values of peak deformation

5 Conclusions

The salt-frost heave of saline soil under freeze-thaw cycles occurs because of volume change under phase transition of crystals of salt and water. Due to the influence of the structure heave of soil, salt-frost heaves show a strong cumulative effect when unloaded soil is exposed to freeze-thaw cycles. Salt-frost heave can be restricted considerably by loading, and there is a critical load of the salt-frost heave cumulative effect.Under this load, peak salt-frost heaves approach a constant, and the residual values become 0, therefore there is no longer structure heave or cumulative effect under freeze-thaw cycles.When the overlying load is smaller than the critical load, the cumulative effect should be taken into account in calculation of salt-frost heave.A salt-frost heave model under freeze-thaw cycles considering cumulative effect is proposed based on our test results. The model is convenient for engineering applications and provides scientific theoretical basis for calculation and maturity evaluation for long-term salt-frost heave of sulfate saline soil foundations in seasonal frost areas of China.

Acknowledgments:

This research is supported in part by the General project of Chongqing Science and Technology Commission Scientific (Grant No. cstc2019jcyj-msxmX0813)and Youth Program of Scientific and Technological Innovation Fund of Gansu Academy of Sciences (Grant No.2019QN-04)and is a part of the Scientific Project of Yangtze Normal University (Grant No. 2017 XJQN16).