ZHANG Huaxing,LI Huaxiong*,HUANG Bing,ZHOU Xianzhong

(1.School of Management and Engineering, Nanjing Universtiy, Nanjing 210093, China;2.School of Information Engineering, Nanjing Audit University, Nanjing 211815, China)

Abstract：The accuracy of face recognition has been able to reach a very high level in recent years. However, many studies on face recognition usually focus on minimizing the number of recognition mistakes while neglecting the imbalance of different misclassification costs, which is not really reasonable in many real-world scenarios.In addition, training a precise classifier often requires a large number of labeled samples, and there is only few labeled samples in many cases.To address this problem, we propose an incremental sequential three-way decision method for cost-sensitive face recognition with insufficient labeled samples, in which a Gaussian mixture model and expectation maximization (EM) algorithm are used to label new samples. We construct a Gaussian mixture model for the whole data of the face images, which mixed the labeled and unlabeled image data via EM algorithm.In many practical applications, the labeled samples are scarce and insufficient. So taking full advantage of the unlabeled samples can help the learned classifier well represent the testing samples and give better results. Instead of minimizing the recognition error rate only, we seek for a balance between recognition error rate and misclassification costs. And we consider a delayed decision, also called the boundary decision, when the labeled images are insufficient. With the increasing available information in the sequential process, the boundary decision can be converted to positive decision or negative decision, thus forming an incremental sequential three-way decision process. The use of sequential three-way decision can decrease the decision costs effectively. The experiments demonstrate the effectiveness of this method.

Key words：face recognition; Gaussian mixture model; EM algorithm; sequential three-way decision; cost sensitive learning

0 Introduction

Face recognition is closely relevant with people’s life and work, and brings us a lot of convenience[1]. Different methods for face recognition have been developed in the past few years[2-4]. Since the outbreak of Corona Virus Disease in 2020, it has exerted a significant and far-reaching impact on the global economy and social life. In this case, the use of face recognition technology for authentication can greatly reduce the chance of people being in close contact and decrease the possibility of virus transmission. Current face recognition technologies have achieved high recognition accuracy[5-7].However, most traditional face recognition systems ignored the fact that different kinds of recognition mistakes generally lead to different amounts of losses in many real-world scenarios. For example, in a security department’s face-tracking system, the impact of wrong recognition of an escaped criminal as an average citizen would be much worse than that of wrong recognition of an average citizen as an escaped criminal. Because the former may leads to more serious consequences than the latter. The examples indicate that it is necessary to consider cost-sensitive classification for face recognition. Zhang and Zhou[8]proposed a study on cost-sensitive face recognition, in which face recognition was taken as a multiclass cost-sensitive learning task. Zhang and Sun[9]introduced a cost sensitive SRC dictionary learning method for face recognition problems.

Despite the relatively mature development of face recognition methods, the lack of labeled images is still one of the most challenging problems in most real-word applications[10]. It is relatively difficult to obtain a large number of labeled samples, because it may require a large amount of labor and resources to obtain these labels. Thus, some studies try to use unlabeled samples to improve the generalization ability of classifiers[11-12]. One of the effective methods is the Gaussian mixture model (GMM), which is essentially a semi-supervised method. GMM can effectively utilize the distribution information implied in the unlabeled samples to make the parameter estimation more accurately. Maetal.[13]used regularized Gaussian fields criterion for non-rigid visible and infrared face registration. Wangetal.[7]used Gaussian distributions for face recognition problems with image sets.

In this paper, we introduce a method involving GMM and EM algorithm to solve the problem of insufficient labeled samples. First, we split the training set into two parts,i.e. labeled pool and unlabeled pool. Labeled pool is used to store labeled samples and a classifier is trained with these labeled samples. And unlabeled pool is used to store a large number of unlabeled samples. We predict their labels with GMM and EM methods, then add the samples with predicted labels into the training set to train a new classifier. In this way, unlabeled samples are gradually added from unlabeled pool to labeled pool, thus forming a sequential process and leading to more and more labeled samples in the training set. The useful information can be gradually increased, and the performance of the classifier will also be improved. This dynamic sequential process actually simulates the process of human behavior decision making and conforms to the three-way decision model.

Three-way decision(3WD) was proposed by Yao[14]based on the rough set theory of decision making. In the past few years, many researchers studied the theory and methods of 3WD, which has been used to solve problems in many areas. Fang and Min[15]presented a framework based on 3WD and discernibility matrix to handle the cost-sensitive approximate attribute reduction problem under both qualitative and quantitative criteria. Lietal.[16]proposed a DNN-based sequential granular feature extraction method and presented a cost-sensitive sequential 3WD strategy based on the sequential multi-level granular features. He and Wei[17]introduced the basic ideas underlying fuzzy logic into the study of three-way formal concept analysis.Liuetal.[18]extended 3WD with incomplete information. Lietal.[19]defined the composite three-way cognitive concepts. Jiaetal.[20]presented a new multiphase cost-sensitive learning method and worded effectively. Lietal.[21]applied sequential 3WD model to the research of cost sensitive face recognition. Yuetal.[22]proposed a new tree-based incremental overlapping clustering method using the 3WD theory. Qianetal.[23]defined a new attribute reduction for sequential 3WD.

Different from the existing work, we consider a semi-supervised method to simulate the process from a small number of labeled samples to a large number of labeled samples under the condition of insufficient labeled samples. In the dynamic sequential process, the labeled information increases gradually, then constructed a sequential 3WD strategy. We consider the total decision cost rather than the misclassification error rate. Finding a minimum of the decision cost in the sequential process and then terminate the decision steps to obtain an optimal policy.

The rest of this paper is organized as follows. We introduce a cost-sensitive sequential 3WD for face recognition in Section 1. In Section 2, GMM and EM methods are used to predict the unlabeled samples, and add useful information to the sequential process. In Section 3 and Section 4, experimental results are presented and analysed. And Section 5 gives a conclusion of the paper.

1 Cost-sensitive sequential three-way decision

1.1 Problem formulation

Most traditional face recognition systems assume that all misclassification cost the same loss and aim to achieve a lower recognition error rate. We argue that this assumption is not reasonable in mary practical applications[8]. As mentioned in section 0, it is quite difficult to get enough information in the first place. In this case, it is better to build a boundary region to make a delayed decisions[24]. For the objects difficult to make decisions, we can put them into the boundary region and make decisions after gathering sufficient information. Making a delayed decision is more cost-effective than making a wrong decision immediately when the information is insufficient. This process leads to a sequential 3WD making, which is similar to the decision making process of human.

For a cost-sensitive face recognition problem,we useS={X1,X2,…,Xn} to denote the facial images set withnsamples. The class label ofXiis represented byli∈{1,2,…,n,…,m}.For clarity, we usePto represent the formernlabels which are positive class labels (gallery subjects), and the restm-nlabels is represented byNas the negative members (impostors). A decision set of a cost-sensitive sequential 3WD model can be described asD={αP,αB,αN}, which means to classify the face image as gallery subject, boundary and impostors. These three decisions can categorize the costs into six types[21]:

1)λPP: The cost of classifying a gallery subject correctly.

2)λNN: The cost of classifying an impostor correctly.

3)λNP: The cost of misclassifying a gallery subject into an impostor.

4)λPN: The cost of misclassifying an impostor into a gallery subject.

5)λBP: The cost of classifying a gallery subject into the boundary for delayed decision.

6)λBN: The cost of classifying an impostor into the boundary for delayed decision.

These six decision results form a cost matrix that is shown in Table 1. Obviously, the classification costs of these six decisions are different from each other. Usually a right decision cause the lowest cost, the cost of a delayed decision is the second, and the cost of a wrong decision is the highest,i.e.λPP≤λBP≤λNPandλNN≤λBN≤λPN. Note that the cost of different types of misclassifications is given by the users according to their needs.

Table 1 Decision costs

1.2 Sequential three-way decision model

3WD consists of positive region, negative region and boundary region, which are corresponding to three kinds of decisions, respectively: acceptance, rejection and non-commitment[25]. For the things with comprehensive information, the judgment of acceptance or rejection can be given directly. As a comparison, those with incomplete information often need further investigation, which is manifested as delayed decision making. For example, when deciding whether the suspect is a criminal, the police release the person who has no obvious motive or evidence for the crime. For those who have solid motive and relevant evidence, the police will judge them as criminals and keep them in custody. For those whose motives are not obvious and whose evidence is unknown, the police will conduct further trials and search for evidence before reaching a conclusion.

3WD model adds the option of non-commitment, that is indecision or delayed decision, which is close to the experience of human cognitive thinking of uncertainty. Considering the updating and supplementation of decision information, Yaoetal.[26]further extended 3WD to sequential 3WD. The sequential 3WD consists of acceptance, rejection, and non-commitment[27].

In the practical applications of face recognition problem, different misclassifications may cause different amount of losses. When the available information is insufficient with a small amount of labeled data, making decisions immediately may be costly. So we choose a delayed decision to decrease the decision cost. For clarity, a sequential 3WD model is described in detail.

Definition1 LetS={X1,X2,…,Xn} be a set of images andD={αP,αB,αN} be a decision set. For an incremental updating data set onS, we assume thatA={X1,X2,…,Xn}={[X]{x1},[X]{x1},{x2},…,[X]{x1},{x2}…,{xn}},i.e.X1?X2?…?Xn, andcost(D|Xi) represents the cost of decidingXiasD. Then we can obtain the sequential 3WD as follows[21]:

SD=(SD1,SD2,…,SDi,…,SDn)=

(φ*(X1),φ*(X2),…,φ*(Xi),…,φ*(Xn)),

(1)

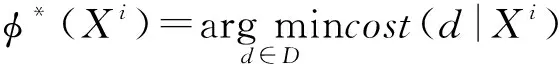
Let Pr(P|Xi) denote the probability of identifying the sample as a gallery subject (positive region) while Pr(N|Xi) as the impostor (negative region). And then we can calculate the decisioncosts(cost(Dj|Xi),j=P,B,N) as follows[21]:

cost(DP|Xi)=λPPPr(P|Xi)+λPNPr(N|Xi)

cost(DN|Xi)=λNNPr(N|Xi)+λNPPr(P|Xi),

cost(DB|Xi)=λBPPr(P|Xi)+λBNPr(N|Xi).

(2)

In this way, three decision costs can be calculated in any steps of the decision. We find the item of minimum cost and use it as the optimal strategy for thei-th step[21]:

(3)

As can be seen from (2) and (3),λijand Pr(P|Xi) are two important parameters to obtain the optimal decisionSDiin a sequential 3WD. The loss functionλijis relatively easy to know. Thus we are more interested in getting the conditional probabilityPr(P|Xi). In this paper, we introduce a method based on GMM and EM algorithm, which can be useful for calculating the probabilities.

2 Cost-sensitive sequential 3WD based on Gaussian mixture model and EM algorithm

In real-world applications, it is more expensive to obtain labeled samples than unlabeled samples. Semi-supervised learning just provides a way to make use of the cheap unlabeled samples[10]. GMM belongs to the generative method of semi-supervised learning, which integrates multiple single Gaussian models to make the model more complex and thus simulate more complex samples. Theoretically, if the number of Gaussian distributions in a GMM is large enough and the weights between them are set reasonably enough, a GMM can fit the samples of any distributions. Therefore, we consider a way using GMM to model the data of the face images. It should be assumed that all data (whether labeled or not) is generated by the same potential GMM. This hypothesis can connect the unlabeled data with the learning target through the parameters of the potential model. The label of the unlabeled data is treated as the missing parameter of the GMM, and then the EM algorithm is used to solve it.

2.1 GMM modeling

We use the GMM to model the face image data and treat different class of people as the Gaussian distributions. GMM consists ofkmixed components, each of which corresponds to a Gaussian distribution. The probability density function of GMM is defined as:

(4)

LetS={(X1,l1),…,(Xn,ln),Xn+1,…,XN} be an image set that consists of both labeled and unlabeled samples, and {(X1,l1),…,(Xn,ln)} denotensamples with labels, {Xn+1,…,XN} are unlabeled samples.

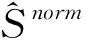
(5)

We divide the calculation of normalized correction into two parts,i.e. the labeled data and the unlabeled data[11]:

(6)

whereaiis the approximately estimated centroid of classli.

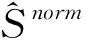
andαj=p(j) be the prior probability of classj. Assume a latent indicatorβi,jto denote the label of unlabeled samples:

(7)

According to Bayes’ theorem, the posterior probability of sampleXjgenerated by thei-th Gaussian distribution corresponding to:

(8)

For (4), when calculating the parameters of GMM model,i.e.

maximization likelihood estimation can be adopted, that is, maximization likelihood

logγi,j=

(9)

We can use (8) and (9) to optimizeθand the cluster labels for each sample are determined as follows:

(10)

2.2 Estimation of GMM by Semi-Supervised EM algorithm

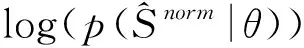
● E-Step: The mixing coefficient of each gaussian distribution is determined by the posterior probabilityγi,j. So we can estimate the potential indicatorβi,jof the unlabeled samples through the current estimate ofθ. According to (7), the label of the labeled data is known, while for the unlabeled samples, the currently estimated parameterθoldis used to calculate the expectation ofβi,j, and get a better estimation ofβi,j:

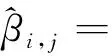
ifi∈{n+1,…,N}.

(11)

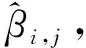
(12)

2.3 Sequential three-way decision based on GMM and EM

As discussed in Section 2.1 and Section 2.2, we get the predicted labels of the unlabeled data. In the iteration process, we take part of the unmarked samples for prediction each time, and add the predicted results as known information into the training set to develop the classifier. Then we use the classifier to classify the samples in the testing set. For each picture, we can getpi,i∈{1,…,n,…,N}, that is the probability that each picture belongs to each class. Then we have:

(13)

Eq(13) gives the conditional probability what the 3WD need. Next step, we set the experiment parameter and compute the cost of 3WD according to (2) and (3). The code of the whole algorithm is shown in Algorithm 1.

Algorithm1 Incremental sequential three-way decision based on GMM and EM.

In the real-world cost-sensitive problems, there is no doubt that sufficient information can develop a good classifier and achieve low misclassification costs. Similarly, continuously adding new labeled samples to a cost-sensitive 3WD can effec-tively reduce the decision risk. We need a process to get more useful information, but it may lead to an increase in test costs. For example, the predicted wrong labels will result in the high time consumption, the cost of labeling samples and the cost of misleading classification. Therefore, it is significant to consider the test cost to properly evaluate the decisions. Generally speaking, test cost increases with the decision steps. So test cost is simply described as test (Ai)=βk2in this paper. The setting of parameterβis shown in Table 2. Then the total cost can be calculated as:

Algorithm 1Input: Initial labeled training set L1Output: Cost of two-way decision C2WD and cost of three-way decision C3WD1: for 1≤i≤kdo2: Train a classifier Ωi using Li;3: Compute the cost Ci2WD and Ci3WD using Ωi;4: Select n samples from U, which make up a pool Ui;5: Initializes the model parameters θ=αj,μj,∑j|j =1,2,…,k} of GMM;6: repeat7: E-Step: Calculate βi,j by using (7) and (11);8: M-Step: Optimize the model parameters θ by (12);9: until Satisfy the termination condition;10: Get the predicted labels of Data in Ui with step 5-9;11: Update the labeled training set Li+1←Li∪Ui;12: end for13: C2WD={C12WD,C22WD,…,Cs2WD};14: C3WD={C13WD,C23WD,…,Cs3WD};15: return C2WDand C3WD.

costtotal=F(costD,costT)=costD+βk2.

(14)

whereβis a coefficient that can be determined based on the actual situation,kis the number of iterations in the sequence. AndcostDdenote the decision cost,i.e. misclassification cost.

3 Experimental section

In order to confirm the effectiveness of our method, we conducted several experiments in this part. Experiments are carried out on three popular databases: PIE, EYaleB and AR. We analyzed the experimental results and compared the performance of sequential 3WD with sequential two-way decision, and verify the superiority of sequential 3WD method in reducing the decision cost.

3.1 Face Databases

Some sample images of the used databases are shown in Fig. 2.

● PIE: The PIE database contains 41 368 facial images of 68 volunteers. 49 face images under various light conditions for each subject are used. All images are cropped to 60×60 pixels.

● EYaleB: The Extended Yale B Database consists of 2 414 face images of 38 subjects, which are captured under 64 different lighting conditions. All images are cropped to 60×60 pixels.

● AR: The AR face database contains 2 600 faces, including 50 males and 50 females. In two sessions, 26 faces images of each person was captured in a variety of lighting conditions.

3.2 Experimental Parameter Setting

All experimental parameter settings are shown in Table 2. From the practical condition of a cost-sensitive sequential 3WD, the number of gallery subjects and impostors are different. We useGto represent the number of classes in gallery subjects andIto denote the number of classes in impostors.LandUare used as the number of labeled and unlabeled samples for each subject in the training set. In different application scenarios, the meaning of cost is different. So instead of setting a specific value for the cost, we change it through a set of ratios,i.e.λPN∶λNP∶λBN∶λBP. The minimum valueλBPis set to be 1, and the cost of classified correctly is 0,i.e.λBB=λPP=0. Actually, the cost of different types of misclassifications is given by the users according to their needs. Therefore, three cost parameters with different proportions are selected to simulate specific application scenarios in the experiment.

λPN∶λNP∶λBN∶λBPPIE databaseEYaleB databaseAR database10∶3∶2∶114∶3∶2∶118∶3∶2∶1

Fig.2 Some samples of PIE(a), EYaleB(b) and AR(c)face databases used in experiments

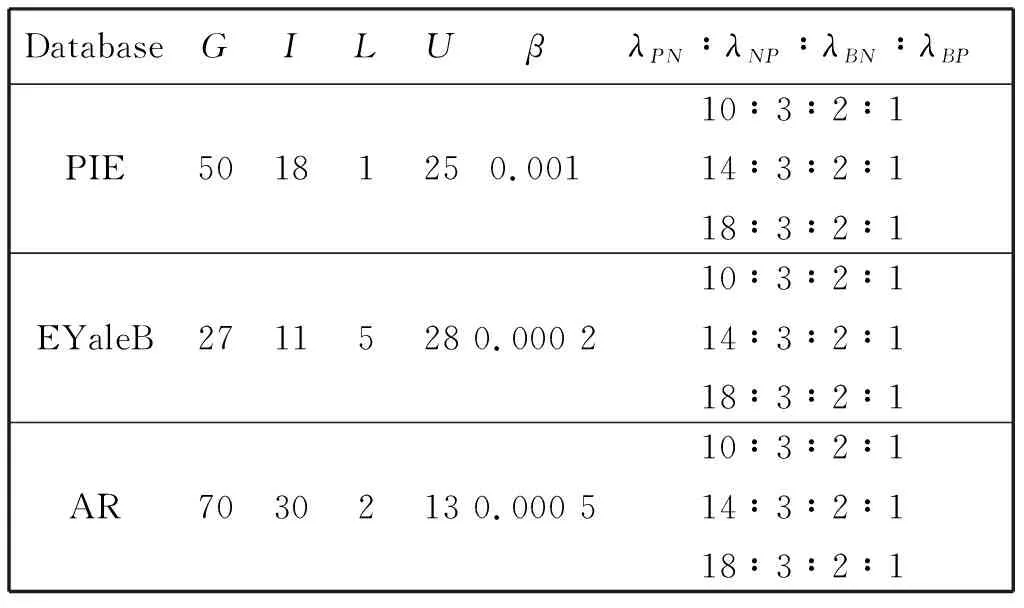
Table 2 Experimental parameter setting

4 Results and Discussion

In this section, we compared the decision cost and total cost of cost-sensitive sequential 3WD with cost-sensitive sequential two-way decision. We used the same parameter settings in Table 2 for each round of experiments. Three items are compared on PIE, EYaleB and AR databases in this section:

1) Decision cost: the misclassification cost of the model.

2) Total cost: decision cost plus test cost.

3) Three regions: The number of samples in three domains varies with the number of decision steps.

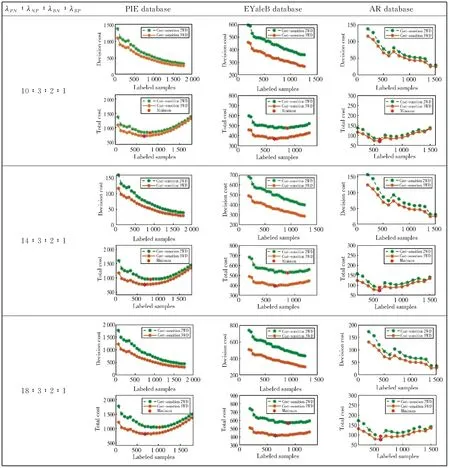
Fig.1 shows the decision cost and total cost on PIE database, EYaleB database and AR database under different proportional cost parameters. The decision cost decreases as the number of labeled samples increases in the sequential process. We use GMM and EM methods to predict the label of unlabeled samples and add them to the training set, thereby increased the information available for decisions. With more available information, the performance of the classifier is improved, thus achieving a higher recognition accuracy rate and a lower decision cost.On the other hand, as the labeled information increases, the test cost increases as well, such as time cost or data cost. Therefore, the total cost,i.e. the sum of decision cost and test cost, will decrease first and then increase. So the sequential decision process can be terminated at the suitable decision steps to minimize the total cost.

From Fig. 1, we know that the decision cost and total cost of sequential 3WD are lower than that of sequential two-way decision. This is due to the effect of boundary decision. In the sequential two-way decision model, people have to make decisions with incomplete information, which may cause a high decision cost. In contrast, the sequential 3WD considered a delayed decision, which forms the boundary region, and added a third alternative to acceptance and rejection. For the objects that are difficult to make decisions, we can put them into the boundary region and make decisions after gathering sufficient information. The cost of making a delayed decision is lower than that of making a wrong decision immediately. Thus the cost of sequential 3WD has a better results than of sequential two-way decision.

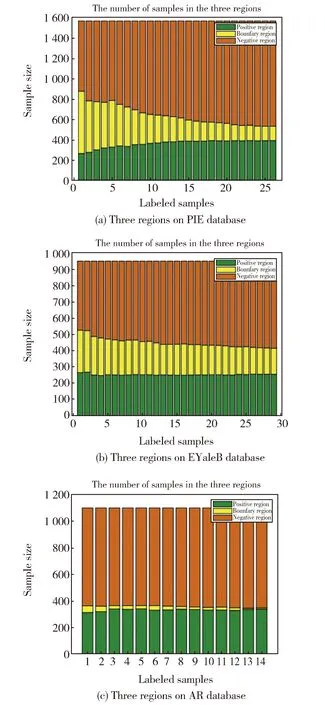
Fig.3 Three regions on PIE(a), EYaleB(b)and AR(c) database

Fig. 3 shows that the number of samples in three domains varies with the number of decision steps. As the number of decision steps increases,the number of samples in the boundary region decreases, the number of samples in both positive and negative regions increases, and the total number of samples in the three domains remains unchanged. When the available information for accurate decision is insufficient, the boundary decision gives an optimal choice, many samples are divided into the boundary region to reduce the decision cost. As more information becomes available and the decisions become more accurate, the samples of the boundary region are gradually divided into po-sitive and negative regions.The experiment results prove the superiority of cost-sensitive sequential 3WD.

5 Conclusion

For the face recognition problem in the real world, we should consider that the cost of misclassification is not equal in different recognition scenarios. On the other hand, the labeled samples are scarce in reality and it is much expensive than unlabeled samples. The lack of available information will lead to the decision uncertainty. For this reason, we propose an incremental sequential three-way decision method for cost-sensitive face recognition with insufficient labeled samples. This mo-del uses the method of GMM and EM algorithm to increase the useful information in the sequential decision process, and seeks for lower cost rather than recognition error rate. The iteration steps will finish at the minimum of total cost to seek for the optimal strategy.Experiments validate that the sequential three-way decision has better performence than traditional two-way decision in terms of decision cost and total cost. And it provides a new strategy to solve the cost sensitive problem.