Li Zhang(張莉), Wenjie Liu(柳文潔), Jiahao Huang(黃嘉豪),?, and Chaohong Lee(李朝紅),?

1Guangdong Provincial Key Laboratory of Quantum Metrology and Sensing&School of Physics and Astronomy,

Sun Yat-Sen University(Zhuhai Campus),Zhuhai 519082,China

2State Key Laboratory of Optoelectronic Materials and Technologies,Sun Yat-Sen University(Guangzhou Campus),Guangzhou 510275,China

Keywords: spinor Bose gases,superfluid-Mott insulator phase transition,Landau–Zener dynamics

1. Introduction

The high degree of tunability of ultracold atoms in period optical potentials enables it to be an excellent platform for simulating the Bose–Hubbard(BH)models.[1–5]The quantum phase transition from a superfluid(SF)phase to a Mott insulator(MI)phase has been widely studied after its realization in scalar Bose–Einstein condensate(BEC)trapped in cubic optical lattice.[2,6–9]It is a second order phase transition for spinless bosons confined in optical lattices,which is characterized by a continuous change of the SF order parameter with the system parameters.[10,11]

As an important fundamental problem, the Landau–Zener (LZ) dynamics has attracted much attention for a long time.[12–22]The original single-particle LZ problem describes the non-adiabatic transition when a two-level system is linearly driven across an avoided level crossing.[23,24]The transition probability is independent of the initially occupied level and given by the celebrated LZ formula.[23,24]The many-body generalization of the LZ problem has been explored in scalar BECs within double-well potentials and its extension, a twochain optical ladder, where population dynamics is studied through linearly sweeping the bias energy between the double wells and the two chains respectively.[12–18,20]Unlike the single-particle LZ process,adiabaticity breaks down in the inverse sweep from the highest level while avoided level crossing remains in the ground-state sweep from the ground state level. This is ascribed by the interparticle interaction which induces a characteristic swallow-tail-shaped loop structure in the high energy levels.[12–15,17,18]

Bosons can possess spin degree of freedom when confined in optical traps.Different from scalar BECs,when spinor BECs are loaded into an optical lattice, the spin-dependent interaction comes to play a role. It can change the spins of two interacting bosons while conserving the total magnetization, which leads to a range of phenomena that are absent in the scalar BECs.[25–30]One important aspect is the change of the nature of the SF–MI phase transition. While the SF–MI phase transition remains second order in ferromagnetic interacting BECs in optical lattice, it can be first order in antiferromagnetic interacting ones.[31–34]The SF–MI phase diagrams for both ferromagnetic and antiferromagnetic interacting BECs have been given by Monte Carlo and mean-field(MF) calculations.[31–34]Recently, the first order nature of the SF–MI phase transition has been experimentally demonstrated in cubic lattice trapped sodium antiferromagnetic interacting BECs.[35]On the other hand, spinor bosons in optical lattices serve as a good candidate to study many-body dynamics.[4,29,36–42]The main dynamical studies have focused on the spin-mixing oscillations in a single site of deep optical lattice,[37,38]nonequilibrium dynamics by quenching the lattice depth or the magnetic field,[39–41]and the coupled dynamics of few atoms in double well.[42]The adiabatic dynamics of the lattice confined spinor BECs, to our knowledge, is rarely uncovered.

The cluster MF approach,as an extension of conventional single-site MF approach, provides an alternative way to simulate BH models.[20,43–48]It decouples the whole system as clusters of multiple lattice sites, where intracluster couplings remain and the clusters interact with the surrounding ones through mean fileds. Thus, it preserves most merits of the spatial correlations but costs relatively small amount of computational resources. The cluster MF approach has been successfully applied to solve the ground-state and many-body LZ problems for bosons trapped in superlattices.[20,43–46]

In this article, we present a theoretical study on the ground-state properties and many-body population dynamics of spin-1 bosons confined in a two-chain lattice ladder by the cluster MF approach. In the framework of our cluster MF treatment, each rung of the ladder is treated as a coherent whole,in which the intra-rung correlation is reserved,and the inter-rung tunneling is decoupled by the MF approximation. For unbiased ladder,we find that the ground states(GSs)include SF phase and integer filling MI (IntMI) phase, the transition between which can be first order at a part of the phase boundary curves. For biased ladder, in addition to the SF phase and IntMI phase, we find a half-integer filling MI(HIntMI)phase, and the transition between the SF phase and the HIntMI phase is always second order. Tuning the bias energy continuously,we report on a change of the SF–MI phase transition nature, accompanied by the variation of the filling number in the MI phase. Furthermore, we analyze the population dynamics by linearly sweeping the inter-chain bias with different sweep rate and initial states,namely,the equilibrium initial states which are the eigenstates of the initial system and the nonequilibrium initial states. We find that, for the equilibrium initial state,the adiabaticity breaks down if the atoms initially occupy the higher chain while it is kept if they initially occupy the lower chain. For nonequilibrium initial states,the spin-dependent interaction leads to rich population dynamics,but does not affect the adiabaticity of the population transfer.

The article structure is as follows. In Section 2, we give the Hamiltonian for our physical system. In Section 3, we present the cluster MF ground-state phase diagrams. In Section 4, we study the population dynamics and analyze the effect of the spin-dependent interaction. In the last section, we summarize our results.

2. Spinor bosons in two-chain ladder

We consider an ensemble of F = 1 bosons confined in a two-dimensional optical lattice created by two pairs of counterpropagating linearly polarized laser waves running in two orthogonal directions. The laser waves form left- and right-polarized standing waves with Rabi frequency ?ν(rν)=?0νcos(kLrν), where ν =x, y represents the propagation direction, and kLis the wave vector of the laser beams. The mF= ±1 sublevels are coupled indirectly by the V and Λ transitions to the excited states caused by the two polarized standing waves. When the detunings are sufficiently large,the effective potential for the atoms in the three degenerate GSs reads as[31,32]

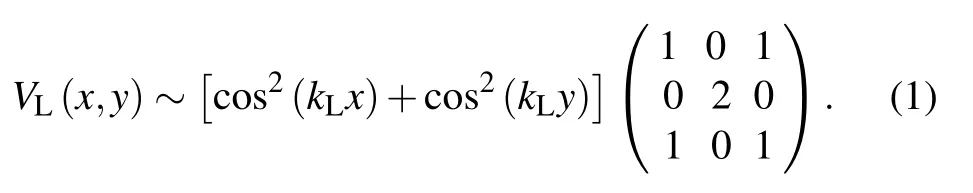
The two lowest Bloch eigenmodes of this potential,denoted by 0 and Λ,can be well seperated from the others.Thus,the tightbinding model in the lowest-band approximation can be reduced to a two-component Bose–Hubbard Hamiltonian.[31,32]Imposing an additional standing wave with wave vector kL/2 along the y direction, we can obtain a series of parallel two-chain ladders. If the barrier between neighboring ladders is sufficiently high, the ladders are decoupled into individual ones. The Hamiltonian for a single ladder, see Fig.1, can be described by a spinor Bose–Hubbard ladder(BHL)

We first consider the unbiased case with ?= 0. Due to the absence of asymmetry, the two chains are equivalent and the order parameters of both chains are always equivalent ψ=ψL=ψR(shí). The phase diagram in this case is shown in Fig.2(a).The SF phase appears when the system is dominated by the tunneling terms. Otherwise, when the on-site interaction term dominates,the IntMI phase appears. Our cluster MF calculation shows that the SF–IntMI phase transition can be first order at a part of the boundaries for each Mott lobe, as indicated by the jump and hysteresis behavior of the order parameters when sweeping the tunneling strength forwards and backwards,see the green and yellow dashed lines in Fig.2(c)for μ/U =0.4. The hysteresis behavior of the order parameters suggests that there exist metastable SF and metastable MI phases in the system. The true SF–MI critical points should be determined by considering the GS properties. Our result contrasts with the case in the simple optical lattice,where the first order phase transition may occur only between IntMI phase with even filling number and SF phase,acquired by single-site MF approach.[31–33,35]

When the spinor BHL is biased, the two chains are no longer equivalent, so the order parameters ψLand ψR(shí)may have different values. However,since the two chains are coupled by interchain tunneling, ψLand ψR(shí)change to zero or nonzero simultaneously as the system parameters vary, see the dotted and dot-dashed black lines in Fig.2(d), where we plot ψLand ψR(shí)as functions of J/Usat ?/Us= ?0.5 andμ/Us=0.4. Thus,we can define the phase diagram according to either of the order parameters.

The phase diagram for ?/Us= ?0.5 is shown in Fig.2(b). In the Mott limit,the intervals ofμ/Usfor different nRon the right chain move upwards by an amount of ??/Us,compared to the corresponding ones on the left chain. Thus,besides IntMI phase, there will appear HIntMI phase where the total particle number is odd. The chemical potential intervals for filling number n and n+1/2 are respectively given by

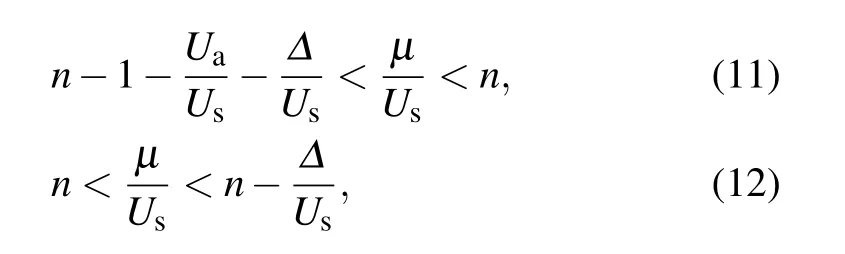
if n is even,and

if n is odd. As J/Usincreases, we find that while the phase transition between the IntMI phase and the SF phase can be first order, that between the HIntMI phase and the SF phase must be second order. The order parameters continuously change from zero in the HIntMI phase to finite in the SF with no hysteresis,see Fig.2(d)withμ/Us=0.4.

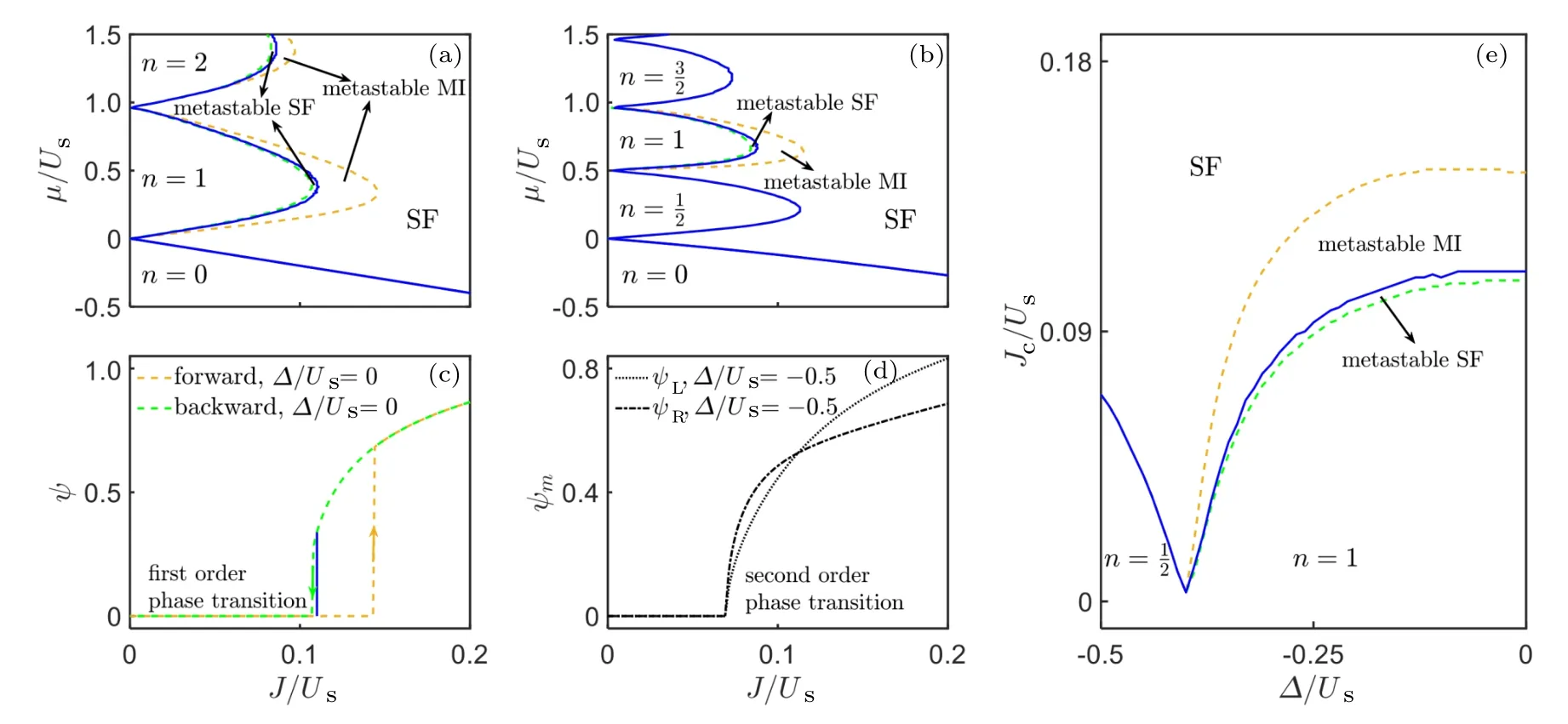
Fig.2. (a)and(b)Ground-state phase diagrams for the unbiased and biased spinor BHL with ?/Us=0 and ?/Us=?0.5,respectively. The IntMI and HIntMI phases are denoted by the filling number n. The blue lines are the true boundaries between the MI and SF phases in the GSs. First order phase transitions are accompanied by the appearance of metastable MI and metastable SF phases. The dashed green and yellow lines denote the MI-metastable SF and metastable MI–SF phase boundaries. (c)The order parameters as functions of J/Us atμ/Us=0.4,and ?/Us=0. First order phase transition accompanied by jump and hysteresis of the order parameters appears when sweeping J/Us forwards(dashed yellow lines)and backwards(dashed green lines). Arrows indicate the sweep direction. The true phase transition point is denoted by the solid blue line. (d)The order parameters ψL and ψR(shí) as functions of J/Us atμ/Us=0.4 and ?/Us=?0.5. Second order phase transition appears with no hysteresis. ψL(dotted black line)and ψR(shí)(dot-dashed black line)vanish continuously at the same value of J/Us. (e)The critical point Jc/Us as a function of ?/Us atμ/Us=0.4. Whenμ/Us+?/Us ＜0,the filling number in the MI phase is 1/2,and the SF–MI phase transition is always second order. Whenμ/Us ??/Us>0,the filling number in the MI phase is 1,and the first order phase transition may appear.

Our results can return to the case of a single ladder in large detuning limit. When|?|is sufficiently large,the spinor BHL can be regarded as two decoupled chains (the potential energy of one chain is much lower than the other). Thus, the GS phase diagrams would recover the ones of a single chain,where the filling number is twice the definition here and only the even-filling MI phases support the metastable states.[31–34]Correspondingly, only integer filling MI phases support the metastable states here.

The above results suggest that one can tune the nature of the SF–MI phase transition by changing the bias energy between the two chains. In Fig.2(e),we show the critical points of the SF–MI phase transition as a function of the bias energy at μ/Us=0.4. When ?/Us=0, the IntMI phase is at unit filling, and the transition to the SF phase is first order. As?/Usdecreases before reaching ?μ/Us,the filling number is unchanged, and the SF–MI phase transition remains first order. After ?/Usdecreases beyond ?μ/Us, the filling number decreases to 1/2,and the SF–MI phase transition becomes second order. Thus,it provides a new approach to control the nature of the SF–MI phase transition by tuning the bias energy.

4. Population dynamics

In this section,we analyze the many-body population dynamics in the spinor BHL.The interchain energy bias ?(t)is linearly swept from negative to positive or vice versa, which is described by ?(t)=?0+vt, with ?0being the initial bias and v denoting the sweeping rate. We consider two typical sweep processes: the direct and the inverse sweeps, and two typical initial states: the equilibrium and the nonequilibrium initial states. In the direct sweep,all the particles are prepared in the lower chain,and the initial bias is set as ?0=?50 and then it is linearly increased from ?0to ?Twith the sweep rate v=(?T??0)/T >0. In the inverse sweep, all the particles are prepared in the higher chain, and the initial bias is set as?0=50 and then ?(t) is linearly decreased from ?0to ?Twith the sweep rate v=(?T??0)/T ＜0. Here T is the total sweep time, and the particles are initial prepared on the left chain for both sweep processes. We consider two typical initial states for the initial condition: the equilibrium initial state |N,0;0,0〉s(for even N) or |N,±1/2;0,0〉s(for odd N),which is a product of the left-chain GS and the right-chain vacuum state; and the nonequilibrium initial state |N,0;0,0〉For|0,N;0,0〉Fwith all particles being either component on the left chain, which makes no qualitative difference. To show the population dynamics, we calculate the fraction of transferred components to the right chain nα,R(t)=〈?nα,R〉(t)/N and the fraction of components remained on the left chain nα,L(t) = 〈?nα,L〉(t)/N. The total particle number is set as N = 10. The interaction and tunneling strengths are set as Us=1 and J =2, respectively. Below, we study the population dynamics for different initial states and sweep rates. The details of the cluster MF algorithm for calculating the population dynamics can be referred to Ref.[20].

We first consider the equilibrium initial state|10,0;0,0〉s,for which n0,L(0)=nΛ,L(0)=0.5. Independent of the sweep rate,the two components transferred to the right chain and/or remained on the left chain are always equal,see Fig.3,where n0,R(t) and n0,L(t) collapse with nΛ,R(t) and nΛ,L(t), respectively. Significant population transfer occurs around ?(t)=0,at which the potential energies of the two chains match. The transfer fractions n0(Λ),Rdepend on the sweep process and rate sensitively. For large sweep rate, both the direct sweep and the inverse sweep are nonadiabatic. The transfer fractions increase rapidly around ?(t) = 0 and keep a specific value which is lower than 0.5,see Figs.3(a)and 3(b)with|v|=50.For small sweep rate, the direct sweep is adiabatic, while the inverse sweep remains nonadiabatic, see Figs. 3(c) and 3(d)with |v|=25. In the direct sweep (v=25), the final transfer fractions n0(Λ),Rreach the perfect limit 0.5 and the remained fractions are zero. In the inverse sweep (v = ?25), the final transfer fractions are still below 0.5 and keep oscillating around a particular value, which means the dynamic process is still nonadiabatic. This adiabaticity breakdown in the inverse sweep has already presented in the LZ dynamics of the many-body scalar BHL,[15–17,20]which is a result of the spinindependent interaction that causes a swallow-tail-shaped loop structure in the energy spectrum.[12–15,17,18]

We then consider the nonequilibrium initial state|10,0;0,0〉Fby preparing ten 0-particles on the left chain. In this case, the spin-dependent interaction plays a role in the population dynamics. We focus on the direct sweep,with the results of the inverse sweep differentiating only by the lower transfer efficiency. Dependent on the sweep rate, different dynamic processes occur. For fast sweep, the transfer of the particles to the right chain is nonadiabatic, see Fig.4(a) with v=50. The 0-particles first partially transfer to the right chain around ?(t)=0,and then interconvert with Λ-particles on individual chains due to the spin-dependent interaction Ua. For slow sweep,the transfer of particles to the right chain is adiabatic,see Fig.4(b)with v=25. The 0-particles transfer to the right chain completely around ?(t)=0,and then interconvert with the Λ-particles on the right chain, which is governed by the dynamics led by the spin-dependent interaction. When the sweep is slow enough that Uais comparable with v/2π, the 0-particles can interconvert with the Λ-particles in time before they are adiabatically transferred to the right chain, see Fig.4(c) with v=1, where n0(Λ),Loscillate with time before?(t)reaches 0. Around ?(t)=0, the two components transfer to the right chain completely and then keep oscillating with time on the right chain. These results imply that while the spin-dependent interaction influences the details of the population dynamics, it has little impact on the transfer efficiency and even nonequilibrium state can be adiabatically transferred to the other chain by tuning the interchain bias.

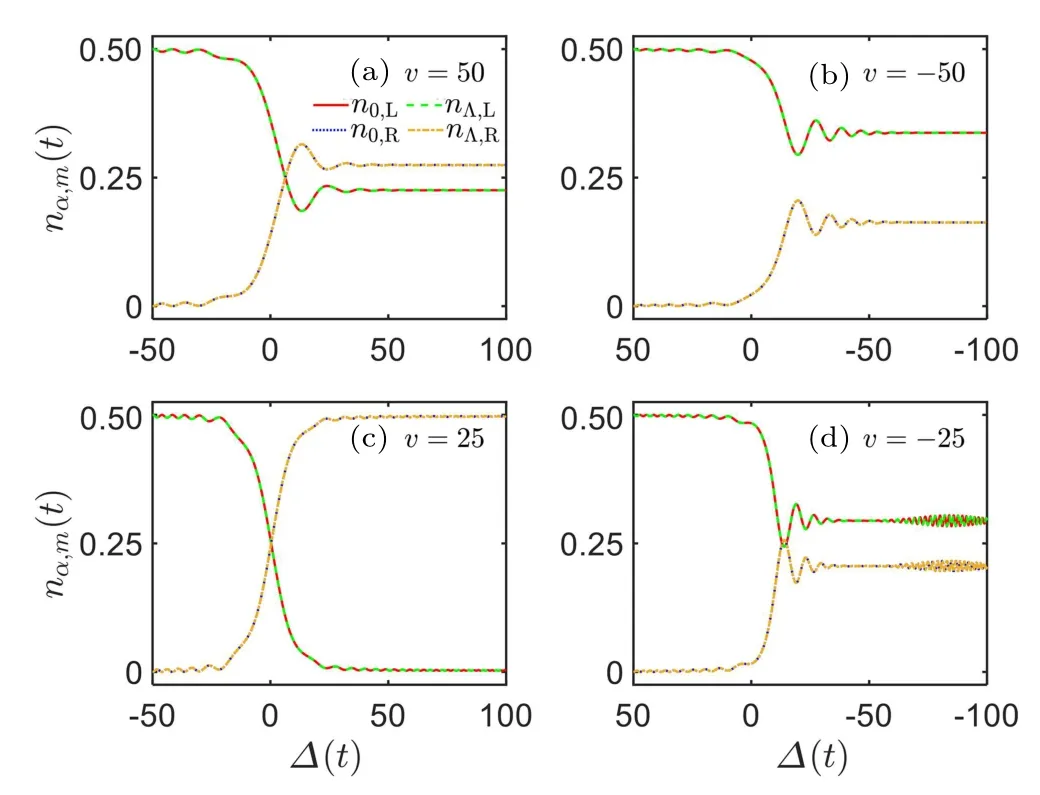
Fig.3. Many-body population dynamics in the spinor BHL for equilibrium initial state|10,0;0;0〉s and different sweep rate. n0(Λ),R(t)and n0(Λ),L denote the fractions transferred to the right chain and remained on the left chain, respectively. The solid red line and the dashed green line denote n0,L(t) and nΛ,L(t), respectively, and collapse with each other. The dotted blue line and the dot-dashed yellow line denote n0,R(t)and nΛ,R(t),respectively, and collapse with each other. The top panel stands for fast sweep:(a) v=50 and ?0 =?50 for direct sweep and (b) v=?50 and ?0 =50 for inverse sweep. The bottom panel stands for slow sweep: (c)v=25 and?0=?50 for direct sweep and(d)v=?25 and ?0=50 for inverse sweep.The system parameters are set as Us=1 and J=2.

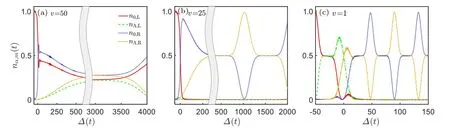
Fig.4. Many-body population dynamics in the spinor BHL for nonequilibrium initial state |10,0;0,0〉F with sweep rate: (a) v=50, (b) v=25,and(c)v=1. The initial bias is set as ?0=?50. n0,L(t),nΛ,L(t),n0,R(t),and nΛ,R(t)are denoted by the solid red,dashed green,dotted blue,and dot-dashed yellow lines,respectively. The system parameters are set as Us=1 and J=2.

To further understand the population dynamics, we calculate the energy spectrum of the system. The entire energy spectrum can be obtained by diagonalizing the Hamiltoian(8)with the order parameters obtained by the self-consistent procedure.[17]In Fig.5, we show the eigenergies as a function of the bias energy for total particle number N = 10.The other system parameters are set as Us= 1 and J = 2.It is clear that there are N+1 bands, each of which features nL= n0,L+nΛ,Land N ?nLparticles on the left and right chains, respectively. When ???1, nLis an integer and decrease from N to zero with the band index; by contrary,it increases from zero to N when ??1. In the lower part of the spectrum, there is an avoided level crossing point between the lowest and the second bands. In the upper part of the spectrum, there forms a loop structure. Thus, for the direct sweep,in which both the equilibrium and nonequilibrium initial states are prepared in the lowest band, the states can cross the avoided crossing point adiabatically without exciting to the second band as far as the sweep rate is small enough.For the inverse sweep,in which the equilibrium and nonequilibrium initial states are prepared in the highest band, adiabaticity breaks down,as indicated by the loop structure.

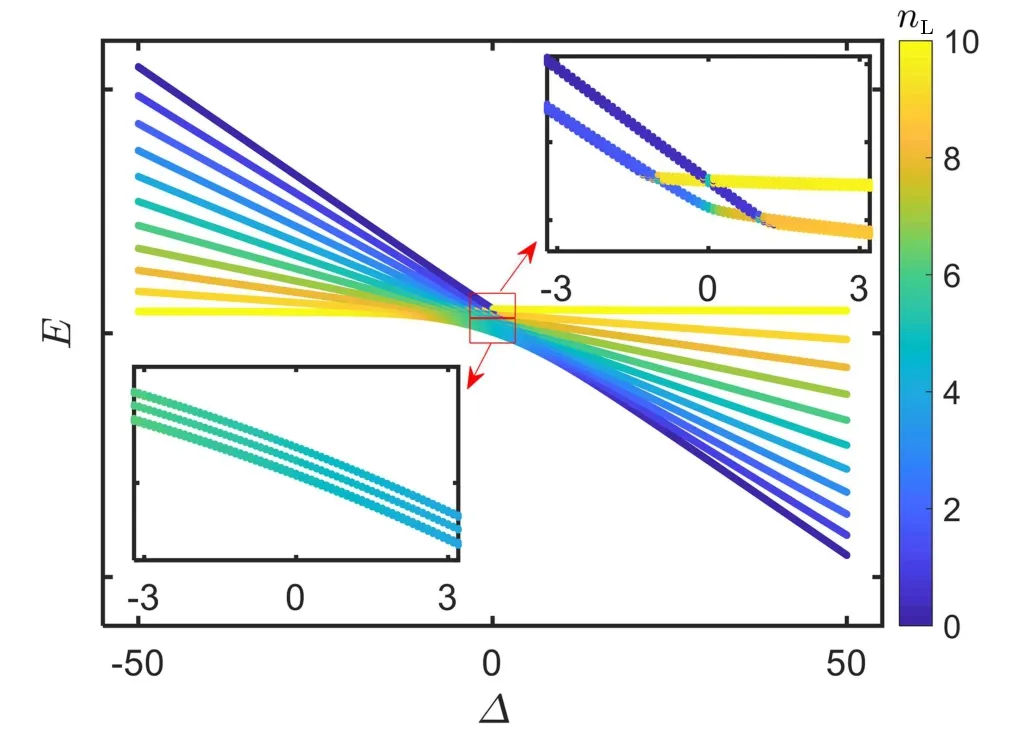
Fig.5. Energy spectrum for total particle number N =10. The color denotes the number of particles on the left chain. Insets on the left lower and right top corners: the magnifications of the lower and upper parts of the energy spectrum around ?=0,respectively. Only the lowest and highest two bands are shown for visualization purpose. The system parameters are set as Us=1 and J=2.

5. Summary

In conclusion,we present a cluster MF study of the static and dynamic properties of spinor sodium atoms confined in a two-chain ladder. For unbiased ladder,the ground-state phase diagram includes the SF phase and the IntMI phase with integer filling number,the phase transition between which can be first order at a part of the boundaries around each Mott lobe.For biased ladder, in addition to the SF phase and the IntMI phase,the HIntMI phase with half-integer filling number may appear. The transition between the SF phase and the HIntMI phase is always second order. Thus,we can change the nature of the SF–MI phase transition by continuously tuning the bias energy.

In the study of many-body population dynamics,we have considered two different kinds of initial states to study the effect of the spin-dependent interaction: the equilibrium and the nonequilibrium initial states. For the equilibrium initial state,the spin-dependent interaction does not influence the dynamic process. The adiabaticity breaks down in the inverse sweep,as in scalar BHL. For the nonequilibrium initial state, the spindependent interaction leads to rich dynamic processes, but does not affect the efficiency of the particle transfer. Even nonequilibrium initial state can be transferred from the lower chain to the higher chain adiabatically.Our results open an avenue to study the dynamics of spinor bosons in optical lattices.

Our findings of the bias tuned SF–MI phase transition and the population dynamics can be observed feasibly in experiments of spinor Bose gases in two-chain ladder.

Acknowledgment

We thank Yongguan Ke and Zhoutao Lei for useful discussion and suggestions.