周玉英

(哈爾濱商業(yè)大學(xué) 基礎(chǔ)科學(xué)學(xué)院,哈爾濱 150028)

1 引言與預(yù)備知識(shí)

用G表示某個(gè)有限群,F*(G)表示群G的廣義Fitting子群,F表示某個(gè)群系. 本文所用術(shù)語(yǔ)和符號(hào)可參見(jiàn)文獻(xiàn)[1-4]. 設(shè)H≤G,如果存在K≤G,使得G=HK且H∩K=1,則稱(chēng)H是G的可補(bǔ)子群或稱(chēng)H在G中可補(bǔ),并稱(chēng)K是H在G中的一個(gè)補(bǔ)群. 特殊子群的可補(bǔ)性質(zhì)對(duì)有限群的結(jié)構(gòu)有重要影響. 例如,G的任一Sylowp-子群均在G中可補(bǔ)當(dāng)且僅當(dāng)G中存在Hallp′-子群[1].

Hall[5]證明了如下經(jīng)典定理:G是可解群當(dāng)且僅當(dāng)G的任一Sylow子群均在G中可補(bǔ). 受Hall定理的啟發(fā),Arad[6]提出了如下猜想: 如果G的任一Sylow 2-子群及任一Sylow 3-子群均在G中可補(bǔ),則G是可解群. Arad等[7]用有限單群分類(lèi)定理證明了Arad猜想,進(jìn)而將Hall定理推廣為如下形式:G是可解群當(dāng)且僅當(dāng)G的任一Sylow 2-子群及任一Sylow 3-子群均在G中可補(bǔ). Miao等[8]引入了M-可補(bǔ)子群的概念: 設(shè)H>1是G的子群,如果存在G的子群B,使得G=HB且對(duì)H的任一極大子群H1,都有H1B1的極小子群,即H是G>1的素?cái)?shù)階子群,則H在G中M-可補(bǔ)當(dāng)且僅當(dāng)H在G中可補(bǔ). Kang[9]引入了弱可補(bǔ)子群的概念: 設(shè)H>1是G的子群,如果存在G的真子群K,使得G=HK,則稱(chēng)H是G的弱可補(bǔ)子群或稱(chēng)H在G中弱可補(bǔ). 易證H在G中可補(bǔ)蘊(yùn)含H在G中弱可補(bǔ),H在G中M-可補(bǔ)也蘊(yùn)含H在G中弱可補(bǔ). 設(shè)H是G>1的極小子群,即H是G>1的素?cái)?shù)階子群,則易證H在G中弱可補(bǔ)當(dāng)且僅當(dāng)H在G中可補(bǔ). 文獻(xiàn)[10-14]討論了可補(bǔ)子群、M-可補(bǔ)子群和弱可補(bǔ)子群的概念和性質(zhì),本文考慮有限群的可補(bǔ)子群對(duì)群結(jié)構(gòu)的影響,所得結(jié)果推廣了文獻(xiàn)[12-15]的相關(guān)結(jié)果.

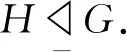
引理4[16]設(shè)p,q是素?cái)?shù),a,b是自然數(shù). 假設(shè)|G|=paqb,則G是可解群.

引理5[17]設(shè)G是非交換單群,p,q是|G|的兩個(gè)不同素因子,a,b是正整數(shù). 假設(shè)存在G的子群H1和H2,使得|G∶H1|=pa且|G∶H2|=qb,則G?PSL(2,7).

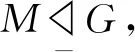
2 主要結(jié)果

定理1設(shè)F是包含全體超可解群的群系,M>1是G的正規(guī)子群,且G/M∈F. 如果對(duì)M的任一極小子群H,H∩F*(GF)均在G中可補(bǔ),則G∈F.

N=N∩G=N∩(HK)=H(N∩K).

注1設(shè)F是包含全體交換群的群系,M是G的正規(guī)子群,且G/M∈F. 易見(jiàn)GF≤M∩G′. 因此,F*(GF)≤F*(M∩G′)≤F*(M)∩G′.

結(jié)合注1,可得如下推論:

推論1[13]設(shè)F是包含全體超可解群的群系,M是G的可解正規(guī)子群,且G/M∈F. 如果F(M∩G′)的任一極小子群均在G中弱可補(bǔ),則G∈F.

推論2[14]設(shè)F是包含全體超可解群的飽和群系,M是G的正規(guī)子群,且G/M∈F. 如果F*(M)∩G′的任一極小子群均在G中弱可補(bǔ),則G∈F.

定理2設(shè)M是G的正規(guī)子群,p是|M|的最小素因子,且P∈Sylp(M). 假設(shè)P的任一極小子群均在G中可補(bǔ),則M在G中p-超循環(huán)嵌入. 特別地,M是p-冪零群.

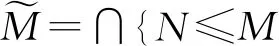
H∩(M∩K)=H∩K=1,

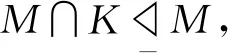
定理3設(shè)M>1是G的正規(guī)子群,且M的任一極小子群均在G中可補(bǔ),則M在G中超循環(huán)嵌入. 特別地,M是超可解群.

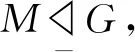
推論3假設(shè)G>1的任一極小子群均在G中可補(bǔ),則G是超可解群.

推論4設(shè)M>1是G的正規(guī)子群,X是G的正規(guī)子群,且滿(mǎn)足F*(M)≤X≤M. 假設(shè)X的任一極小子群均在G中可補(bǔ),則M在G中超循環(huán)嵌入. 特別地,M是超可解群.

證明: 由定理3可知X在G中超循環(huán)嵌入,故F*(M)在G中超循環(huán)嵌入. 由引理7可知M在G中超循環(huán)嵌入. 特別地,M是超可解群. 證畢.

推論5設(shè)F是包含全體超可解群的飽和群系,M>1是G的正規(guī)子群且滿(mǎn)足G/M∈F,X是G的正規(guī)子群且滿(mǎn)足F*(M)≤X≤M. 假設(shè)X的任一極小子群均在G中可補(bǔ),則G∈F.

證明: 由推論4可知M在G中超循環(huán)嵌入,由引理6可知G∈F. 證畢.

定理4如果G的任一奇數(shù)階Sylow子群均在G中可補(bǔ),則G是可解群.

證明: 先證明G的任一合成因子都是素?cái)?shù)階群. 用反證法. 假設(shè)存在G的合成因子K/L,使得K/L不是素?cái)?shù)階群,則K/L是非交換單群. 由引理4知|π(K/L)|≥3,由引理3易檢驗(yàn)K/L滿(mǎn)足該定理的全部條件,即K/L的任一奇數(shù)階Sylow子群均在K/L中可補(bǔ). 特別地,K/L滿(mǎn)足引理5的全部條件. 由引理5知K/L?PSL(2,7),但168階單群PSL(2,7)中沒(méi)有Hall 3′-子群(否則PSL(2,7)同構(gòu)于A3的一個(gè)子群,矛盾),故K/L?PSL(2,7)的任一Sylow 3-子群均不是可補(bǔ)子群,矛盾. 從而G的任一合成因子都是素?cái)?shù)階循環(huán)群,進(jìn)而G是可解群. 證畢.

注2定理4的條件“G的任一奇數(shù)階Sylow子群均在G中可補(bǔ)”不能削弱為“G的任一奇數(shù)階Sylow子群均在G中弱可補(bǔ)”.

例1令G=PSL(2,7)×3,則|G|=23×32×7. 由于在PSL(2,7)中有24階子群,從而G中有72階子群,即G的任一Sylow 7-子群均在G中可補(bǔ),從而在G中弱可補(bǔ). 對(duì)任一R∈Syl3(G),注意到PSL(2,7)

定理5設(shè)|π(G)|=n,其中n≥3. 假設(shè)存在|G|的(n-1)個(gè)互不相同的素因子p1,p2,…,pn-1,使得對(duì)任一1≤i≤n-1,G的任一Sylowpi-子群均在G中可補(bǔ). 如果G的任一合成因子均不同構(gòu)于PSL(2,7),則G是可解群.

證明: 先證明G的任一合成因子都是素?cái)?shù)階群. 用反證法. 假設(shè)存在G的合成因子K/L,使得K/L不是素?cái)?shù)階群,則K/L是非交換單群. 由引理4知|π(K/L)|≥3,由引理3易見(jiàn)K/L滿(mǎn)足該定理的全部條件,由引理5知K/L?PSL(2,7),與G的任一合成因子均不同構(gòu)于PSL(2,7)矛盾. 于是證明了G的任一合成因子都是素?cái)?shù)階群,從而G是可解群. 證畢.

注3注意到|PSL(2,7)|=23×3×7,并且PSL(2,7)的任一Sylow 2-子群及任一Sylow 7-子群均在PSL(2,7)中可補(bǔ),但PSL(2,7)為非交換單群,進(jìn)而是非可解群. 因此,定理5的條件“G的任一合成因子均不同構(gòu)于PSL(2,7)”必不可少.

由定理5可得如下推論.

推論6[15]設(shè)|π(G)|=n,其中n≥3. 假設(shè)存在|G|的(n-1)個(gè)互不相同的素因子p1,p2,…,pn-1,使得對(duì)任一1≤i≤n-1,G的任一Sylowpi-子群均在G中可補(bǔ). 如果G的任一截?cái)嗑煌瑯?gòu)于PSL(2,7),則G是可解群.