Speeding up generation of photon Fock state in a superconducting circuit via counterdiabatic driving?
Xin-Ping Dong(董新平), Xiao-Jing Lu(路曉靜), Ming Li(李明), Zheng-Yin Zhao(趙正印), and Zhi-Bo Feng(馮志波)
School of Science,Xuchang University,Xuchang 461000,China
Keywords: photon Fock state,superconducting circuit,counterdiabatic driving
1. Introduction
Analogous to conventional cavity quantum electrodynamics (QED),[1,2]a one-dimensional transmission line resonator (TLR) generates a quantized electromagnetic field,which can be strongly coupled to artificial atoms of superconducting quantum circuits.[3–9]The on-chip system consisting of atom–light interaction constitutes a device of circuit QED in the microwave range.[10,11]By taking advantage of circuit QED, the explorations of quantum information science and fundamental laws have attracted increasing attention in recent years.[12–18]In the context of quantum information processing,generating microwave photon Fock states in circuit QED is an interesting research subject.[19–25]Experimentally,by the method of stimulated Raman adiabatic passage(STIRAP),the generation of microwave photon Fock states has been demonstrated using the setup of superconducting circuit QED.[26]However, the adiabatic operations within relatively long evolution times were easily affected by decoherence sources.
To perform fast and robust quantum operations, a set of technique named as shortcuts to adiabaticity (STA)[27,28]has been exploited to coherently control over superconducting quantum circuits both theoretically and experimentally.[29–38]The method of STA mainly consists of invariant-based inverse engineering,[39]counterdiabatic driving,[40]and fast-forward approach.[41]The central idea of STA-based operation is that a quantum system can be rapidly evolved from a given initial state to a desired final state in an adiabatic-like process by engineering Hamiltonian. Without the restriction of adiabatic theorem, the same goal as the adiabatic case can be realized but in a shorter time. Quantum operation of interest can be completed in a fast way, which significantly mitigates the decoherence effects of noisy environment.[42]Meanwhile,within a given coherence time, the number of high-fidelity quantum operations could be increased considerably.
Very recently,a theoretical scheme has been proposed for the generation of microwave photon Fock states in a circuit QED by the method of invariant-based STA,[43]in which Rabi couplings were specially designed via polynomial ansatz for implementing the coherent process. Differently, although the pulse profile of counterdiabatic driving is generally continuous and smoothed,the counterdiabatic driving behaving as an auxiliary term needs to be added to a reference Hamiltonian.[44,45]In this case,the control variable of auxiliary driving could enhance the complexity of experimental manipulation. Thereby,the generation of photon states based on the technique of STA with feasible and effective Rabi drivings is highly preferable.
In this paper,we develop a theoretical scheme for speeding up adiabatic generation of photon Fock state via counterdiabatic driving. A transmon qubit is dispersively coupled to a cavity field of TLR. By applying classical drivings to the composite system,we deal with a Λ-configuration interaction.Based on two Gaussian-shaped Rabi drivings,a single-photon Fock state can be generated adiabatically by the method of STIRAP. To speed up the adiabatic operation, we adopt the technique of STA to obtain two modified Rabi pulses, making the process accelerated remarkably. In contrast to the adiabatic counterpart, the shortcut-based operation is significantly insensitive to the decoherence effects. Thus,the protocol could offer a potential approach to optimally create photon Fock states with superconducting quantum circuits.
This paper is organized as follows.We present a transmon qubit coupled to a TLR in Section 2. Section 3 briefly deals with the generation of single-photon Fock state by the method of STIRAP.Section 4 focuses on an accelerated operation by modifying the Rabi drivings in a shortcut manner. The decoherence effects are numerically analyzed in Section 5. Discussion and a conclusion are finally drawn in Section 6.
2. A composite system of a transmon qubit coupled to a TLR

With no radiations from the quantized field and classical driving,the Hamiltonian of the static CPB system,consisting of the charging energy and Josephson coupling, is described by
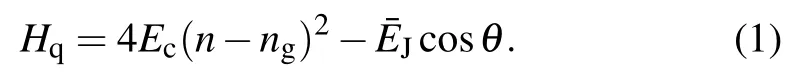



Fig.1. (a) Schematic setup of a transmon-regime CPB coupled to a quantized electrical field of TLR and a classical driving ?Vs. (b)The energy level diagram of the composite system regarding the transmon qubit dispersively coupled to the cavity field.
The qubit is electrically coupled to the cavity mode of TLR,the coupling strength of which is λ, much smaller than the detuning δ =ωr?ωq. In the dispersive regime,the qubit–cavity system can be characterized by the Jaynes–Cummings Hamiltonian[26]

3. Single-photon Fock state generation via STIRAP



where tfis the final time, ?0indicates the amplitude peak of Rabi drivings,τ and σ represents the pulse-related parameters.As demonstrated in Fig.2(b),these two drivings are applied to the composite system in a STIRAP-like sequence.
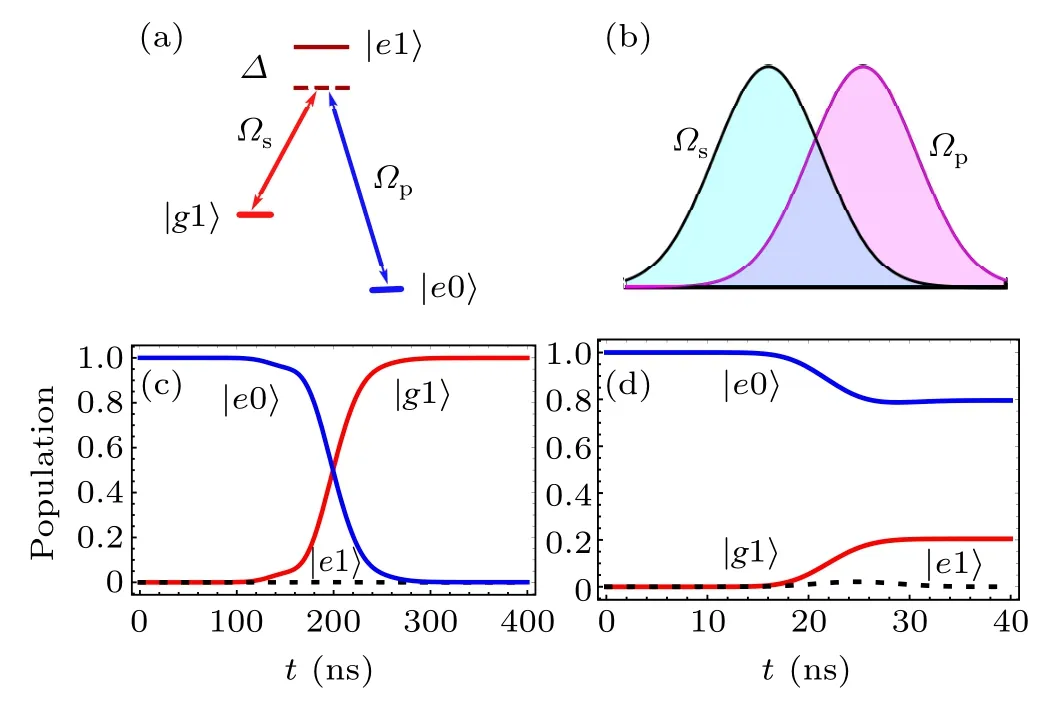
Fig.2. (a)With a common detuning ?,two microwave drivings induce the state transitions between |e1hand |g1h(|e0h) with Rabi rates ?s (?p), respectively. (b) Two Gaussian-profile Rabi drivings ?s and ?p are applied to the three-state system in a STIRAP-pulse order. (c)In the adiabatic case,population transfer from |e0hto |g1hcan be realized in a time t =400 ns.(d)An incomplete transfer from|e0hto|g1hinduced by two non-adiabatic drivings ?s(t)and ?p(t)with t ∈[0,40 ns].


4. Accelerated generation of single-photon Fock state via STA

where ?tsand ?tsare related to ?and ?p,sby

To the reference Hamiltonian Hts,a counterdiabatic driving Hcdis given by[44,49]


5. Decoherence mitigation and negligible leakage errors



- Chinese Physics B的其它文章
- Micro-scale photon source in a hybrid cQED system?
- Quantum plasmon enhanced nonlinear wave mixing in graphene nanoflakes?
- Restricted Boltzmann machine: Recent advances and mean-field theory*
- Nodal superconducting gap in LiFeP revealed by NMR:Contrast with LiFeAs*
- Origin of itinerant ferromagnetism in two-dimensional Fe3GeTe2?
- Intercalation of germanium oxide beneath large-area and high-quality epitaxial graphene on Ir(111)substrate?

