SEQUENCES OF POWERS OF TOEPLITZ OPERATORS ON THE BERGMAN SPACE?
(陳泳)
Department of Mathematics,Hangzhou Normal University,Hangzhou 311121,China
E-mail:ychen227@gmail.com;ychen@hznu.edu.cn
Kei Ji IZUCHI
Department of Mathematics,Niigata University,Niigata 950-2181,Japan
E-mail:izuchi@m.sc.niigata-u.ac.jp
Kou Hei IZUCHI
Department of Mathematics,Faculty of Education,Yamaguchi University,Yamaguchi 753-8511,Japan
E-mail:izuchi@yamaguchi-u.ac.jp
Young Joo LEE?
Department of Mathematics,Chonnam National University,Gwangju 61186,Korea
E-mail:leeyj@chonnam.ac.kr
Abstract We consider Toeplitz operators Tu with symbol u on the Bergman space of the unit ball,and then study the convergences and summability for the sequences of powers of Toeplitz operators.We first charactreize analytic symbols ? for which the sequenceforfconverges to 0or∞as k→∞in norm for every nonzero Bergman function f.Also,we characterize analytic symbols ? for which the norm of such a sequence is summable or not summable.We also study the corresponding problems on an infinite direct sum of Bergman spaces as a generalization of our result.
Key words Bergman space;Toeplitz operator
1 Introduction
For a given positive integer n,we let B=Bnbe the unit ball in the complex n-space Cn.The Bergman space A2=A2(B)is the closed subspace of L2=L2(B,V),consisting of all holomorphic functions on B where V denotes the Lebesgue volume measure on B normalized to have total mass 1.We will use the notation
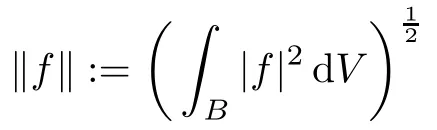
for functions f∈L2.Also,we let H∞denote the space of all bounded holomorphic functions on B.Let P be the Hilbert space orthogonal projection of L2onto A2.For a bounded function u on B,the Toeplitz operator Tuwith symbol u is defined on A2by

In Section 4,as generalizations of our results obtained in Section 3,we study the corresponding problems on an infinite direct sum of Bergman spaces.
2 Preliminaries
Since every point evaluation is a bounded linear functional on A2,there corresponds to every a∈B a unique kernel function Ka∈A2which has the reproducing property

where the notation〈,〉denotes the usual inner product in L2given by
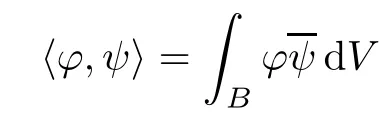
for functions ?,ψ∈L2.The function Kais the well-known Bergman kernel which can be given by
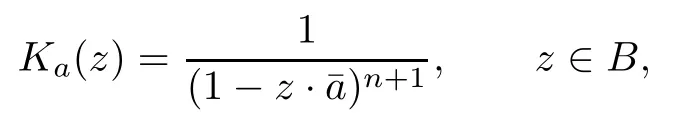


for every f∈A2,which is also a simple consequence of the well-known fact thatis subnormal and therefore hyponormal.
3 Results

for every integer k≥0,we have(b)by the Lebesgue dominated convergence theorem.Finally,implication(b)?(a)is a consequence of(2.3).The proof is complete. □
In the next two theorems,we study the characterizing problem of ?∈H∞when the sequencesconverge to∞as k→∞for every nonzero f∈A2.The notation D denotes the unit disk in the complex plane.
Theorem 3.2For ?∈H∞,the following conditions are equivalent:

for every integer k≥0.In particular,we have
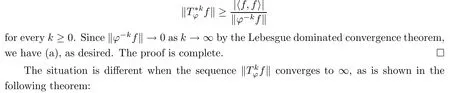
Theorem 3.3Let ?∈H∞.Then the following conditions are equivalent:
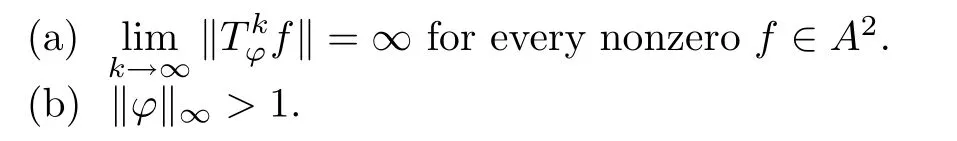
ProofFirst,by a simple application of Theorem 3.1,we see that(a)?(b)holds.Now assume(b)and show(a).Put
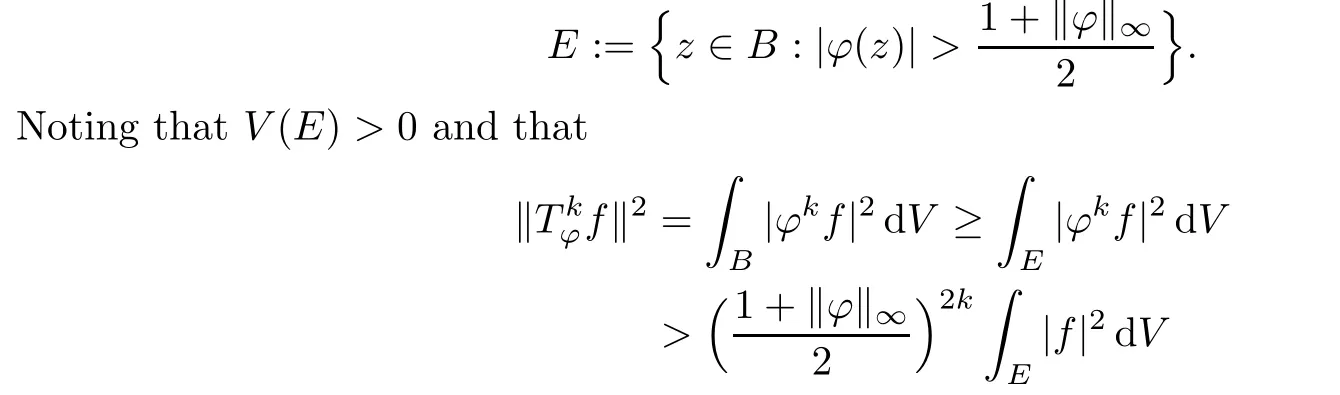
for every integer k≥0 and nonzero f∈A2,we see that(a)holds,as desired.The proof is complete. □

Theorem 3.4Let ?∈H∞be a nonzero function and let 0 ProofFirst(a)?(b)is trivial.Now assume(b)and show(c).Suppose that ?(B)∩D/=?.Then|?(a)|<1 for some a∈B,and hence which contradicts(b).Thus we have(b)?(c).Finally assume(c)and show(a).Then ??1∈H∞and‖??1‖∞≤1.It follows that for every f∈A2and integer k≥0,so(a)holds.The proof is complete. □ As an immediate consequence of Theorem 3.4,we have For a bounded linear operator L on A2,we let||L||edenote the essential norm of L,which is the distance between L and K,the set of all compact operators on A2;namely, Lemma 3.6For ?∈H∞,we have ProofFirst assume(a)and show(c).Suppose that‖?‖∞>1.Then there is a∈B such that|?(a)|>1,and hence In order to prove this,we divide the proof into three steps. Step 1Fix 0<δ<1 and put σ0=1.Choose a sequence{σ?}?≥1of positive numbers satisfying that Then we have Also,we see that and hence Now,for s≥1,suppose that f0,f1,...,fsand t1,t2,...,tssatisfy conditions(6),(7)and(8).Similarly,one can see that there exist an integer ts+1>0 and a function fs+1in A2with‖fs+1‖=1 for which and that fs+1⊥fifor every i with 0≤i≤s,which finishes the induction.We note from(3.7)that Step 3Denote It follows from(3.3)that for all f∈A2 Finally,(2.3)shows that(b)?(a)also holds.The proof is complete. □ for every nonzero function f∈A2. ProofSuppose that(a)holds.By Theorem 3.7,we have that‖?‖∞≥1.If neither(b1)nor(b2)holds,then‖?‖∞=1 and ? is non-constant.Then|?(a)|<1 for every a∈B,and hence for every nonzero function f∈A2.Thus(a)?(b)holds. Suppose that(b)holds.If(b1)holds,then Theorem 3.3 shows that(a)holds.Also,if(b2)holds,then clearly(a)holds.Finally,if(b3)holds,(3.9)shows that(a)also holds.The proof is complete. □ Generally,it seems difficult to characterize ?∈H∞satisfying condition(b3)above,even on the unit disk D.In the case of Hardy space,it is known that the corresponding condition can be characterized by an extremal point condition for the closed unit ball of the space of all bounded holomorphic functions on D;see Chapter 9 of[3]and Proposition 4.8 of[1]for details. We let B be the closed unit ball of the space H∞(D)of all bounded holomorphic functions on D.Also,we let H2(D)be the usual Hardy space on D and let||||H2(D)denote the Hardy norm.Note that H2(D)?A2(D)with||g||≤||g||H2(D)for all g∈H2(D).Thus,if(b3)holds,then Corollary 3.8 shows that for all f∈H2(D).Hence,by Proposition 4.8 of[1],? is an extreme point of B.Thus(b3)implies that ? is an extreme point of B,but we do not know whether the converse is also true.Let us see a simple example in regards to this.Consider ?=z.Then ? is an extreme point of B and is increasing on[0,1),we see that and(b3)holds. In this section,we study the corresponding problems on an infinite direct sum of Bergman spaces as generalizations of results obtained in Section 3. and hence(c)?(b)holds.Finally,implication(b)?(a)follows from(4.1).The proof is complete. □ As a generalization of Theorem 3.2,we have the following result: The following proposition generalizes Theorem 3.3: so(b)holds.Finally implication(b)?(a)follows from(4.1).The proof is complete. □
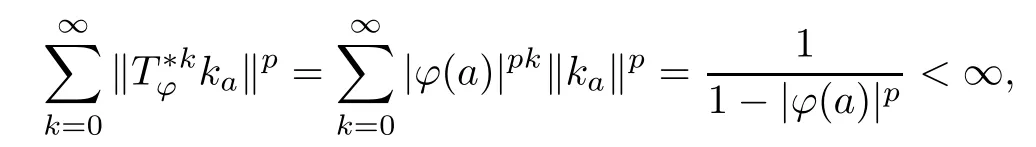
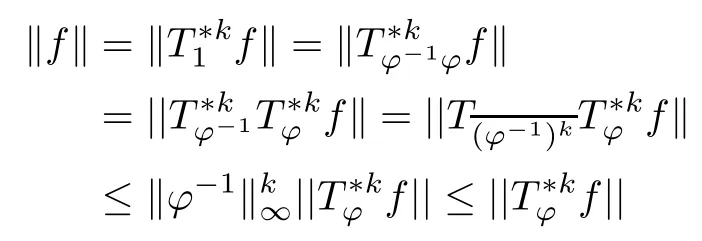



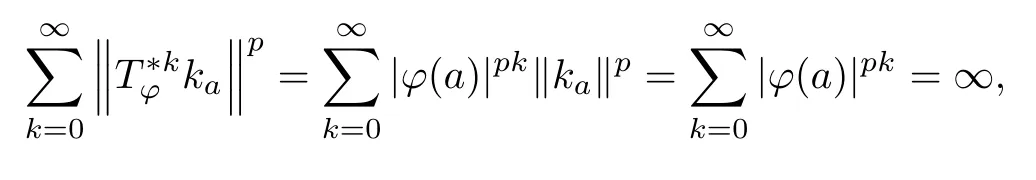
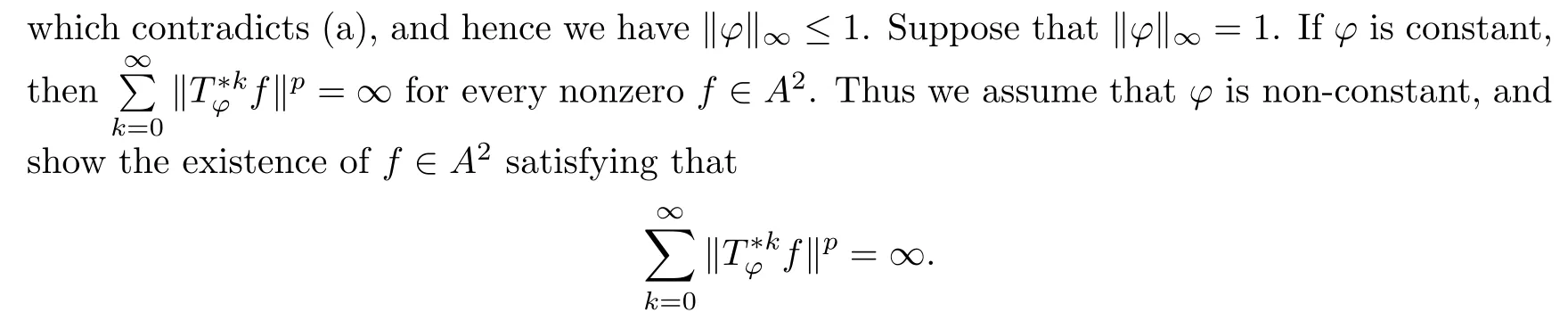


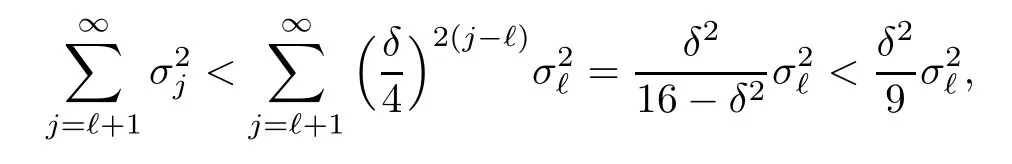


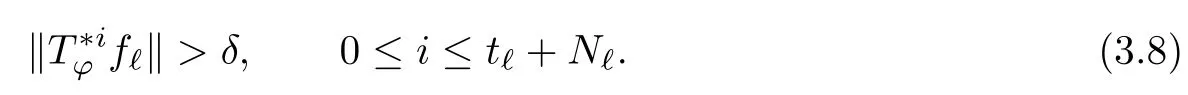
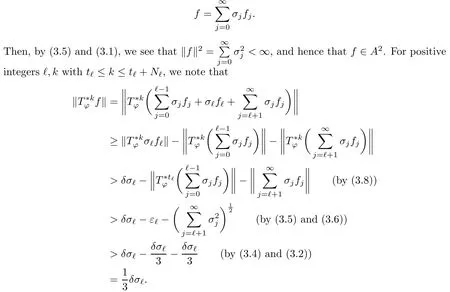

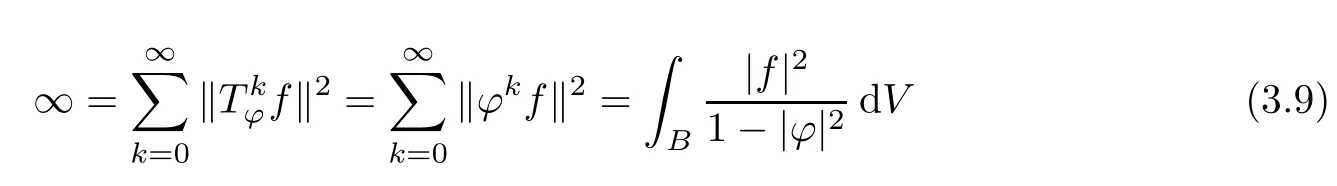
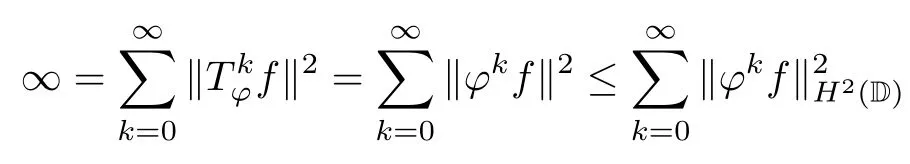

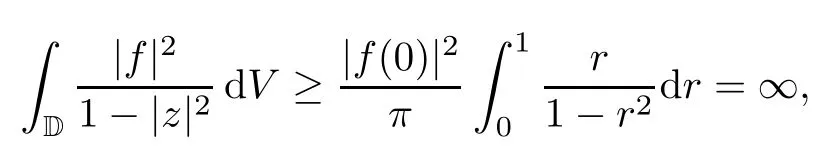
4 A Generalization to an Infinite Direct Sum





 Acta Mathematica Scientia(English Series)2021年3期
Acta Mathematica Scientia(English Series)2021年3期
- Acta Mathematica Scientia(English Series)的其它文章
- A REMARK ON GENERAL COMPLEX(α,β)METRICS?
- GLOBAL WEAK SOLUTIONS TO THE α-MODEL REGULARIZATION FOR 3D COMPRESSIBLE EULER-POISSON EQUATIONS?
- MULTIPLE SOLUTIONS FOR THE SCHRDINGER-POISSON EQUATION WITH A GENERAL NONLINEARITY?
- HOMOCLINIC SOLUTIONS OF NONLINEAR LAPLACIAN DIFFERENCE EQUATIONS WITHOUT AMBROSETTI-RABINOWITZ CONDITION?
- SHARP BOUNDS FOR TOADER-TYPE MEANS IN TERMS OF TWO-PARAMETER MEANS?
- THE PROXIMAL RELATION,REGIONALLY PROXIMAL RELATION AND BANACH PROXIMAL RELATION FOR AMENABLE GROUP ACTIONS?
