Jiangdong Qiu(邱疆冬) Zhaoxue Li(李兆雪) Linguo Xie(謝林果) Lan Luo(羅蘭) Yu He(何宇)Changliang Ren(任昌亮) Zhiyou Zhang(張志友) and Jinglei Du(杜驚雷)

1College of Physics,Sichuan University,Chengdu 610064,China

2Key Laboratory of Photonic and Optical Detection in Civil Aviation and Atmospheric Lidar Institute,Civil Aviation Flight University of China,Guanghan 618300,China

3Center for Nanofabrication and System Integration,Chongqing Institute of Green and Intelligent Technology,Chinese Academy of Sciences,Chongqing 400714,China

Keywords: weak measurement,quantum measurement,accuracy analysis

1. introduction

The concept of weak measurement was introduced by Aharonov, Albert, and Vaidman in 1988.[1]Through about

30 years of development, there are many worthy investigations both in fundamental and application. On one side,weak measurement and weak value are interesting phenomenons as they assist us in understanding many counterintuitive quantum results. On the other side, strange characteristics that weak values can even exceed the eigenvalue range of a typical strong or projective measurement and are usually complex, have allowed a wide range of applications in classical and quantum contexts. Especially,a new parameter estimation method based on weak measurement process, called weakvalue amplification technique, is rapidly growing, which has shown significantly advantages for precision metrology. The essence of weak-value amplification technique,when the preand post-selected states are almost orthogonal, can result in large weak values that can be used to sensitively determine unknown parameters affecting the state evolution, where the parameters are extracted from the coupling pointer shift.

The weak-value amplification technique has been utilized in many scenarios for ultra small physical quantity estimations, such as tiny lateral displacement,[2]light angular deflections,[3,4]angular rotations,[5]longitudinal phase shift,[6]asymmetric spectral response,[7–9]polarization-dependent loss,[10]velocity measurement,[11]high-precision temperature measurement,[12,13]ultra-small angular velocitiy,[14]and so on.Furthermore,there are a series of analyses about its advantageous performance for measurement precision in certain kinds of experimental imperfections,such as detector saturation,[15]temporally correlated noise,[16]decoherence,[17]and more reported in Refs.[18,19].

To completely discuss the technical advantage of the weak-value amplification technique, it is necessary to make clear the effect of noise. In fact, previous research shows that it amplifies the signal while keeping the technical noises caused by the experimental imperfections,e.g.,devices resolution,[2,20]unchanged resulting in the improvement of signal to noise ratio (SNR). However, in the ideal case, the statistical noise or called shot noise,cannot be suppressed via the amplification of the signal and is counterbalanced by the small rate of post-selection.[21–23]More than that, the weakvalue amplification technique is also deemed suboptimal,[24]even fails to suppress technical noise.[25]

Despite all of these, there are a variety of theoretical[26,27]and experimental efforts to optimize the weakvalue amplification technique, such as using technical noise,[28]entanglement,[29–32]squeezed state,[33]recycled photons,[34–36]and beyond the weak-value amplification,e.g.joint weak measurements,[37–39]projective photon-counting measurements.[40]Most of the work mainly concentrate on the average displacement of the pointer to measure tiny physical quantity, meanwhile it is of efficiency to use the postselected photon number[40–43]to realize the measurement of tiny physical quantities[44–46]and the estimation of quantum states.[47–49]

In fact,on the one hand,we should explore the fundamental significance of the weak-value amplification technique,on the other hand, it is also important to investigate and analyze the optimization of the existing protocol of the weak-value amplification technology. Especially in many specific protocols,the main noise source is relatively clear. This allows us to analyze the noise more pertinently and choose better suppression methods. In this paper,we analyze the precision by using pointer shift and photon number counting in the presence of phase errors and pointer resolution. When the photon counting scheme is used,we discuss the relative accuracy of the system in the presence of phase error by using the orthogonal and nonorthogonal pre-and post-selected states,respectively. For the pointer shift measurement scheme, we discuss the measurement accuracy in the presence of phase error,pointer resolution,and statistical uncertainty. These results give a guide way to get the smallest relative precision and deepen our understanding about weak measurement.

2. The framework for pps measurement

We consider the weak measurement process, which can be described as follows. Firstly,the system and meter are initially prepared inρ=|ψ〉〈ψ|andρm=|ψm〉〈ψm|respectively.Then the system and the meter,in the time interval(ti,tf),undergoes the weak interaction, which is given by the Hamiltonian

The last step is post-selection. In this process, we have two different treatments for measurement results. One is, we are only concerned about the probability of finding the system in the post-selected state. When post-selectingΠφ=|φ〉〈φ|on the system, we obtain the detected probability of the system state|φ〉

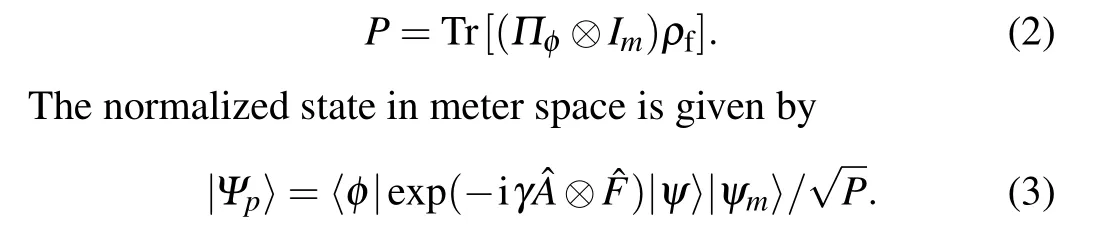
The above two equations show that after post-selection a single particle to be selected with probabilityPin Eq. (2) has the probability distribution|Ψp(F)|2. When the above process repeatsNtimes, the detecting process can be regarded as a number ofN-independent eventsq,which has the probabilityPto be one otherwise to be zero,and the detected numbernis the binomial distributionn ～B(N,P). The detected number isn=∑Ni=1qi,of which the detected number concentrates on

3. Photon number counting

In this section, we analyze such the measured parameter accuracy,where the parameter is extracted from the probability of finding the system in the post-selected state which is realized by measuring the post-selected photon number. We systematically analyze the precision with the orthogonal and nonorthogonal pre-and post-selected states in the presence of phase error. In realistic experiments,the systematic phase errors due to device imperfections cannot be avoided. For simplicity, we summarize all these in a phase errorε. When we use photon counting method, the pixel or digitization noise

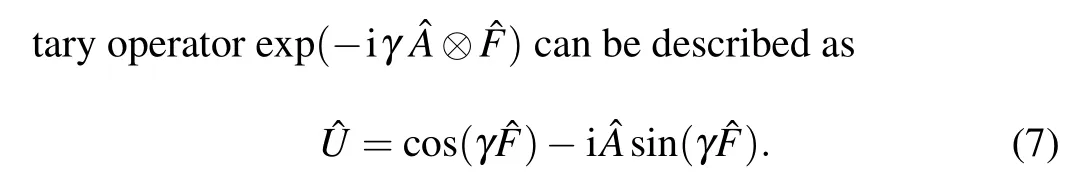
Then taking Eq.(7)into Eq.(2),without approximations,the post-selected probability is obtained as

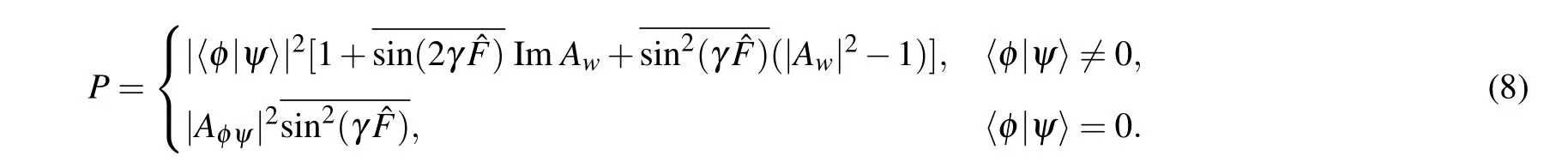
whereAφψ=〈φ||ψ〉. From Eq. (8), there are two ways to extract the informationγ.

First,we consider the pre-and post-selection is orthogonal, which has been used already in the measurement of the spin Hall effect of light,[45]and discussed in Refs. [52,53].Here the weak approximationγ(+?F)?1 is supposed,the probability is

From Eq. (16), we can see that the relative precision is dependent on two factors. One is the phase error, which can be reduced by optimizing the experimental system. The other is the input photon numbers that we can increase to improve the relative precision.

Secondly,we consider the case that pre-and post-selected states are nonorthogonal.Under the condition thatγ|Aw|(?F+?1(the second-order term inγhas been neglected),the post-selected probability in Eq.(8)can be rewritten as

where we take two measurements to get two opposite weak values±|ImAw|. Through the difference betweenP1andP2,the parameterγcan be calculated by

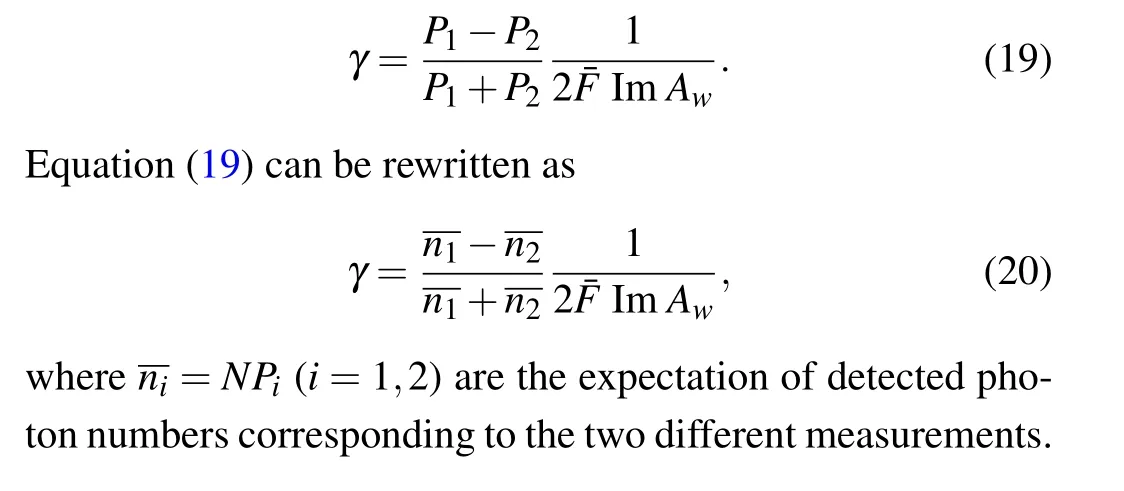
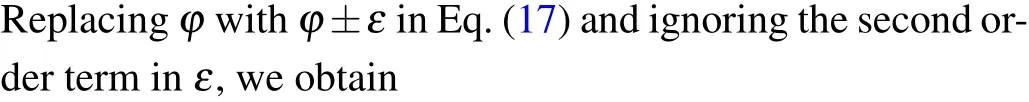
Considering the statistical uncertainty, the realistic detected numbers are given by

wherenεi=NPεi(i=1,2). Replacingn1andn2in Eq. (20)withnε1andnε2in Eqs.(23)and(24),the parameter including the errorγεis obtained with

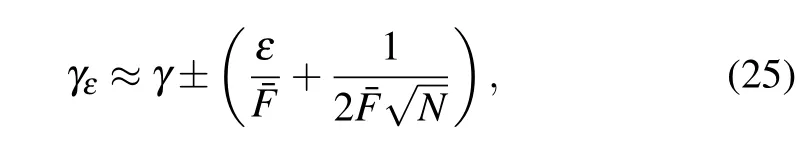
and the absolute accuracy is given by

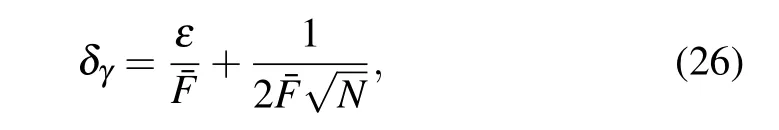
which shows that in addition to reducingεand increasingN,we can also increase the expectation valueto improve the absolute accuracy for the measurement ofγ.

By comparing Eqs. (15) and (26), we can get their absolute precision under specific experimental conditions. According to this absolute accuracy, we can choose a suitable measurement scheme in the situation that the pre- and postselections are orthogonal or not.

Now we have studied about the way by using photon number counting to realize the ultra-small parameter measurement and obtained its precision under the statistical uncertainty and phase error. Next, we study the accuracy of the parameter to be measured using the pointer shift.

4. Pointer shift

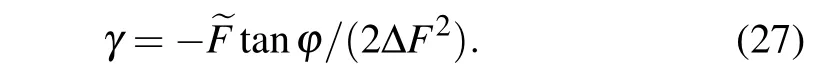
Next,we will discuss the accuracy for the measurement of parameterγin two cases. One is in the existence of phase error and pointer resolution,the other is in the existence of statistical uncertainty.

First, considering the influence of phase errorεand pointer resolutionδFon the parameterγ, equation (27) can be rewritten as

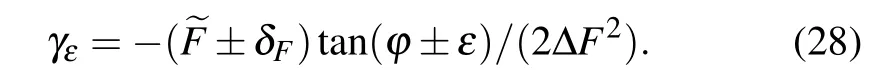
Expanding it and neglecting the second-order term,we obtain The first item shows that under certain resolution increasing weak value can decrease relative precision. However the second item shows that under certain phase error decreasing the weak value can decrease relative precision. The smallest relative precision condition is given by

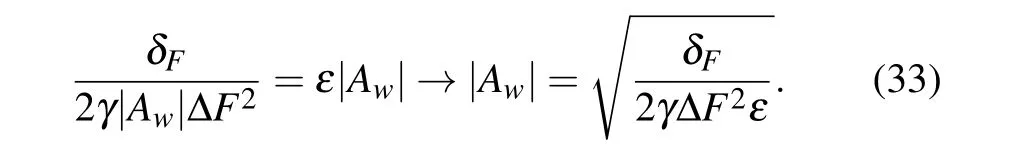
Combining Eqs.(32)and(33),we obtain the smallest relative precision

Under the condition thatδF,ε,andγare determined, we can improve the relative precision by increasing the statistical uncertainty ?F.

In Ref. [21], by replacingδFandεwithand?respectively, the authors have given the absolute accuracyεδF/(2?F2). But in some practical situations,the relative accuracy is also an important criterion.influenced by the weak value. Putting them into Eq. (36), it can be rewritten as

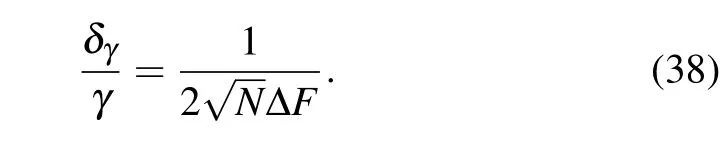
We find that the relative precision is only related to the initial state of the system and meter, that is, the total number of photons and the uncertainty of the pointer. And it is irrelevant to pre- and post-selected states of the system,i.e., the weak value. Therefore,it is not possible to improve the relative precision by adjusting the weak value under the condition of only considering the statistical uncertainty of the pointer shift.

In this part, we consider the use of the pointer shift to measure parameters. When the phase error and pointer resolution are taken into account, the minimum relative accuracy is given. In the existence of the statistical uncertainty,we give the relative precision,which is only relevant to the input total number and the standard deviation of the pointer.

5. Conclusion

In this paper,the statistical uncertainty of photon number and phase error have been introduced theoretically,and the parameter measurement accuracy based on weak measurement has been discussed. When using the photon counting scheme,we have investigated the relative accuracy of the system in the case of phase error by using orthogonal and non-orthogonal pre-selected states and post-selected states respectively. The measurement accuracy with phase error, pointer resolution,and statistical certainty have also been investigated. These results provide a guidance for obtaining minimum relative accuracy and deepening understanding of the weak measurement.