Song Wang(王松) Qihui Ye(葉起惠) Xudong Chen(陳緒棟)Yanzhu Hu(胡燕祝) and Gang Song(宋鋼)

1School of Modern Post,Beijing University of Posts and Telecommunications,Beijing 100876,China

2School of Science,Beijing University of Posts and Telecommunications,Beijing 100876,China

3International School,Beijing University of Posts and Telecommunications,Beijing 100876,China

Keywords: surface plasmon polaritons,chirality,Goos–Hanchen shift

1. Introduction

During the past couple of years, the optical sensors at macro- and nano-scales have been investigated, and surface plasmon polaritons (SPPs) play an important role in these devices, such as sensors, detectors, even in quantum key distributions.[1–18]Goos–H¨anchen (GH) shift is a small shift of light in the total internal reflection, which is quite sensitive to the surrounding medium.[1–10,12]Many applications are introduced in both theory and experiments,such as sensors,[3–5]resonance devices,[6]and switches based on Kretschmann configuration involving Kerr nonlinear medium.[7]Kretschmann configuration is a well-known configuration in SPP excitation.[7,12,19–22]GH shift can be directly measured in the experiment and can reach 100 times the incident wavelength.[7]If the medium in the Kretschmann configuration is chiral,GH would display a new function for detecting the chirality of the medium.

Chiral objects have many applications in bio-medicine and bio-agriculture.[23,24]Left-handed objects are beneficial to humans.Right-handed objects are harmful to pests and help to make a good harvest of the crops. Hence,it is very important to distinguish between left-handed and right-handed objects.During the recent works,SPPs and localized surface plasmons(LSPs)can enhance the electromagnetic fields in the near field and significantly amplify the chiral optical response.[25–42]Circular dichroism(CD)spectra are used to describe the chirality of the objects in a wide wavelength regime.[25–39]If we use the GH shift to replace the CD spectrum, the difference between the left molecules and the right molecules can be directly measured in the experiment,and we do not need to make a distinction of a small value between absorptions or scatterings.

In this paper, we investigate a chiral molecule detector based on the lateral shift splitting/GH shift splitting in Kretschmann configuration involving chiral tri (diethylene glycol monobutyl) citrates (TDBCs) by using classical methods. Kretschmann configuration is made up of a gold film sandwiched between the dielectric medium and left TDBCs or right TDBCs. Incident light is injected from the dielectric medium with an incident angle. Fresnel equations and the stationary phase method are employed to solve our proposed structure. The parameters of chiral TDBCs and Au film are changed to show the impact on the sensitivity of the molecule detector. Due to the direct measurement in the experiment,our structure has potential applications in distinguishing the chirality detector.

2. Calculation models and results

whereimeans left(L)or right(R),?∞=n2bg, andnbg=1.33 is the index of the background.ωiis the resonant frequency of TDBCs, andγiis the damping constant of TDBC.fiis the oscillator strength, which depends on the molecular concentration. According to the experimental measurement of TDBC,we obtain thatωL=3.228×1015rad/s,ωR=3.203×1015rad/s, andγL=ωR=8.195×1013rad/s.[35,36]Incident chiral beam is composed of TE-polarized beam(Es)and TMpolarized beam(Ep)asEs+Epe±iπ/2. In Kretschmann configurations, only the TM-polarized beam can be used to generate SPPs. Here, we only consider TM-polarized beam is injected into our proposed system.

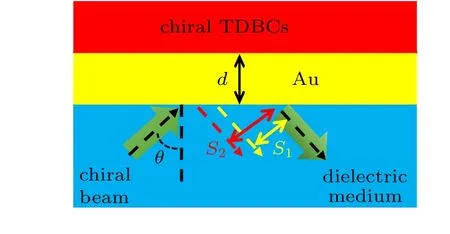
Fig.1. The sketch of our calculation model.

GH shiftSis calculated by the classical method as[2,7]

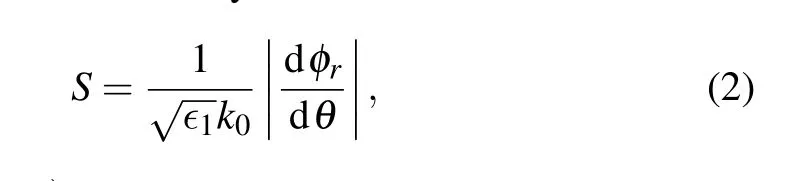
whereφr=Im(lnr) is the phase ofr, andris TM-polarized reflection coefficients of Fresnel equations for Kretschmann configurations.[2,7,12]The reflectionRis calculated asR=|r|2.Before we discuss the relation between the GH shiftSand the incident wavelengthλ, it should be mentioned that the incident angleθis equal to the surface plasmon resonant angleθSPPs.[2,7,44]In our calculation, the incident angle is changed with the incident wavelength. The best condition of SPP excitation is the angle being equal to the surface plasmon resonant angleθSPPs. In order to obtain a significant GH shift for each wavelength in calculations,we set the incident angleθchanging with the incident wavelength. In the application, we may set the incident angleθis equal toθSPPsat the resonant wavelength of left TDBCs or right TDBCs. In the following, we calculate Kretschmann configurations with only LTDBCs and Right TDBCs to study normalized GH shiftS/λand the difference of normalized GH shifts between Kretschmann configurations with LTDBCs and RTDBCs ?S/λ.

3. Results and discussion

First, we choosefi=0.01 andd=20 nm to calculate the reflection spectrumRand normalized GH shiftsS/λwith both LTDBCs and RTDBCs,respectively. The incident angle is considered asθSPPs. The results are shown in Fig. 2. Furthermore,the difference of normalized GH shifts ?S/λis also plotted in Fig.2.

Due to the interactions between SPPs and chiral TDBCs,normalized GH shiftsS/λare amplified near the resonant frequencies of chiral TDBCs,as shown in Fig.2(a). They are as 24 times of LTDBCs and 10 times of RTDBCs as the incident wavelength. Due to the different resonant wavelengths, the positions of the maximumSfor LTDBCs (λ=577 nm) and RTDBCs (λ=582 nm) do not overlap. As Fig. 2(b) shown,the difference of normalized GH shifts ?S/λcan reach 24 atλ= 577 nm. It seems that the reflected beam with LTDBCs moves a lot, but the one with RTDBCs hardly moves atλ= 577 nm. This phenomenon can be easily measured in the experiment, and LTDBCs and RTDBCs are easily distinguished. Also, the working wavelength can be taken asλ=582 nm.

Then, we decrease the thicknessdof Au film to show how ?S/λchanges. The thicknessdis changed from 20 nm to 50 nm with the step of 10 nm. The results are shown in Fig.3. For each thickness of the proposed system,Si/λis also calculated and shown in the inserted picture.

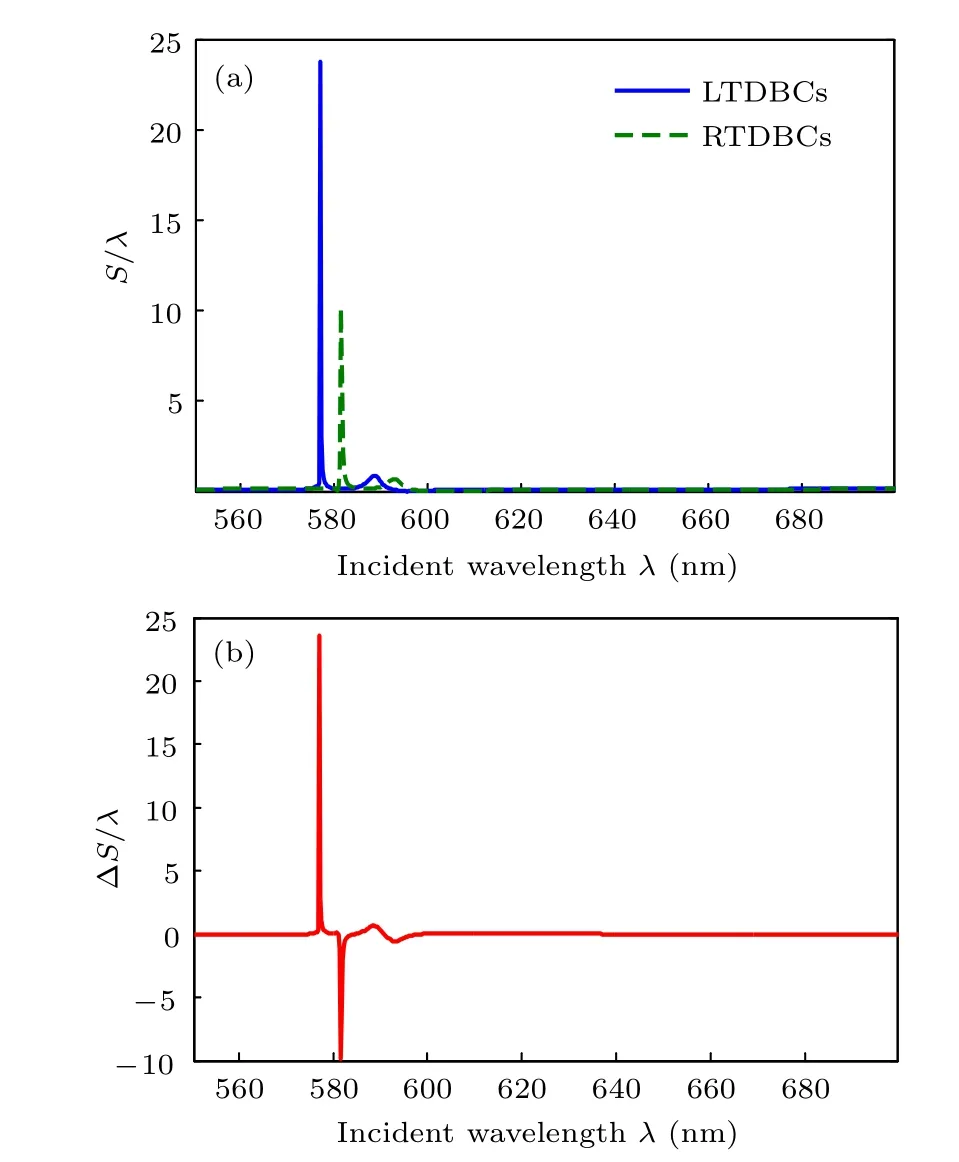
Fig.2. Normalized GH shifts Si/λ (a)and the difference of normalized GH shift ?S/λ (b)versus the incident wavelength λ,respectively.

As shown in Fig. 3, the working wavelength of our proposed structure is changed by the thickness of Au filmd. At the same time, the value ofSi/λdecreases. The dissipation of Au film increases sharply with the thickness of Au film increasing, while the decoupling conversion rate decreases. It means that there are more SPPs joining into the interaction between chiral TDBCs and Au film with the increase of Au film thickness. According to the analysis above, we can change the working wavelength by tuning the thickness of Au film.With the increase ofd,the working wavelength has a red shift.Although there are more SPPs interact with chiral TDBCs,the intensity of ?S/λis reduced by the large dissipation.Comparing the intensity of ?S/λ,we also find that with the changes ofd,there is an optimal thickness to make ?S/λthe largest. We pick the maximum values and the positions of ?S/λfor both LTDBCs and RTDBCs by changingdwith the step of 0.5 nm.The results are shown in Fig.4.

As shown in Fig.4(a),there is a little difference between the optimal thicknesses for LTDBCs and RTDBCs.The largest?S/λis larger than 100, which can be significantly observed in the experiments. The positions of the maximum of ?S/λfor LTDBCs and RTDBCs almost do not overlap. The phenomena above are mainly caused by the different resonances for left TDBCs and right TDBCs. Besides the incident angleθis equal toθSPPs,there is an optimal thickness of Au film which shows the best ability to coverts light into SPPs coupling with chiral TDBCs and decouple into light around the resonant wavelengths of chiral TDBCs. It reflects the competition between the dissipation and the conversion efficiency from light to SPPs. If the thickness of Ag film is less than the skin depth of light(less than 15 nm),light may directly go through Ag film without the electromagnetic field enhancement and couple with chiral TDBCs. This means that the chirality of TDBCs may not be amplified. According to our calculations, we’d better choose a suitable thickness of Au film to obtain obvious phenomenon for chiral TDBCs detecting in experiments.

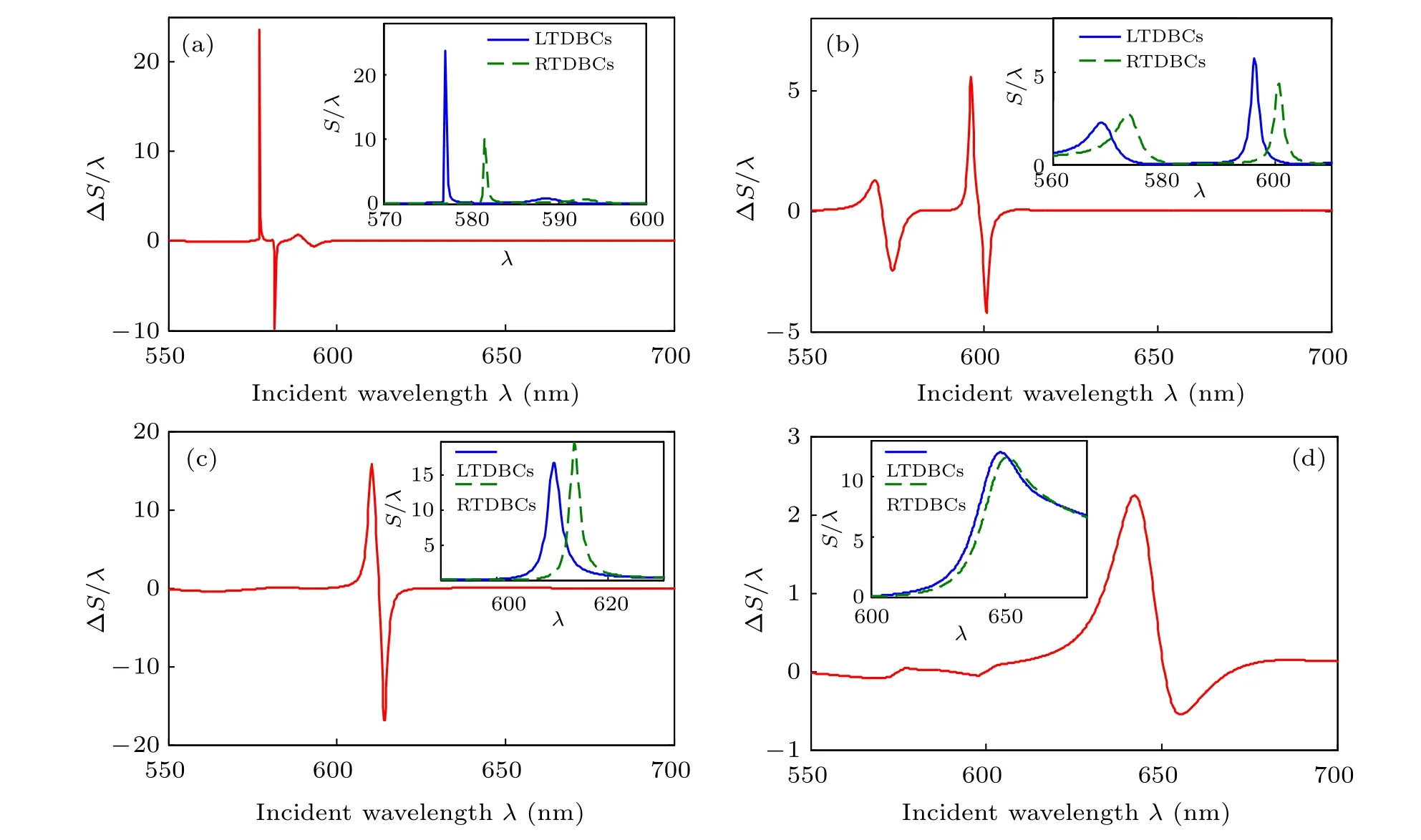
Fig.3. The difference of normalized GH shift ?S/λ versus the incident wavelength λ with Au film thickness d changing from 20 nm to 50 nm with the step of 10 nm,respectively. Normalized GH shifts Si/λ versus the incident wavelength λ for each d is in the inserted picture.

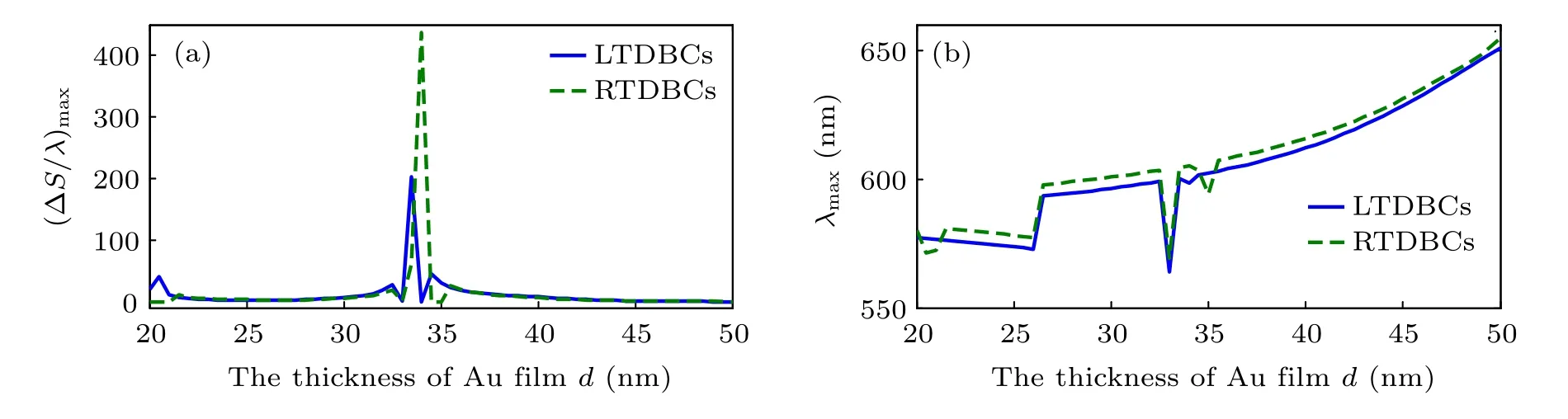
Fig.4. The maximum values(a)and the positions(b)of ?S/λ for both LTDBCs and RTDBCs by changing d with the step of 0.5 nm,respectively.

Table 1. The values of the peaks and dips in ?S/λ.

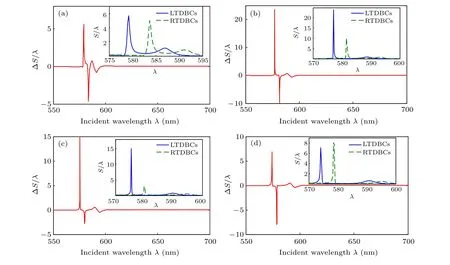
Fig.5. The difference of normalized GH shift ?S/λ versus the incident wavelength λ with coupling strength f changing from 0.008 to 0.014 with the step of 0.002,respectively.Normalized GH shifts Si/λ versus the incident wavelength λ for each f is in the inserted picture.

Finally,we show the impact of the oscillator strengthfon?S/λ. We change a small step of 0.002 to show the sensitivity of our proposed structure.fis changed from 0.008 to 0.014,and ?S/λversusλare shown in Fig.5.Si/λis also inserted in the figures for eachf.

As Fig.5 shown, the peaks and the dips of ?S/λhave a slight shift(within 5 nm)due to a quite small change off.The values of the peaks and the dips in ?S/λchanges a lot. This is because thatfhas great influences on?3andθSPPs.Hence,the value of ?S/λchanges a lot. We list the values of the peaks and the dips in Table 1.We find that althoughfchanges a little 0.002,the difference of GH shifts between peak values or dip values is no less than 5 times of the incident wavelength,about 2.9μm. This difference is easy to observe in the experiment.

4. Summary

In summary, we investigate a high sensitive chiral molecule detector based on GH shift in Kretschmann configuration involving chiral TDBCs. Fresnel equations and the stationary phase method are employed to calculate the lateral shift/GH shift. Due to the interaction between SPPs and the chiral TDBCs, the GH shifts in our proposed structures with two kinds of chiral TDBCs are amplified at different wavelengths. GH shift can reach 24 times the incident wavelength and be easily observed in the experiment. The working wavelength of the detector can be tuned by the thickness of the Au film. We also find there is an optimal thickness to make ?Sthe largest,which is over 100 as the incident wavelength and can be easily observed in experiments. Furthermore, we discuss the oscillator strengthfand find that our proposed detector is quite sensitive withf. By changing 0.002 forf, the change of ?Sis no less than 5 times the incident wavelength, which is about 2.9 μm at our working wavelength. Our proposed structure is very sensitive and has potential applications in experiments.