廣東省珠海市斗門(mén)區(qū)第一中學(xué)(519000) 李凱

2019年全國(guó)高中數(shù)學(xué)聯(lián)賽江蘇賽區(qū)市級(jí)選拔賽第8 題是一道求值域的題,本題看似簡(jiǎn)單,但對(duì)高中學(xué)生來(lái)講,得到最終答案非常不易,筆者經(jīng)過(guò)探究找到了這類(lèi)值域問(wèn)題的統(tǒng)一解法.

一、題目展示與解法探究

(一)方法分析

(二)典例剖析

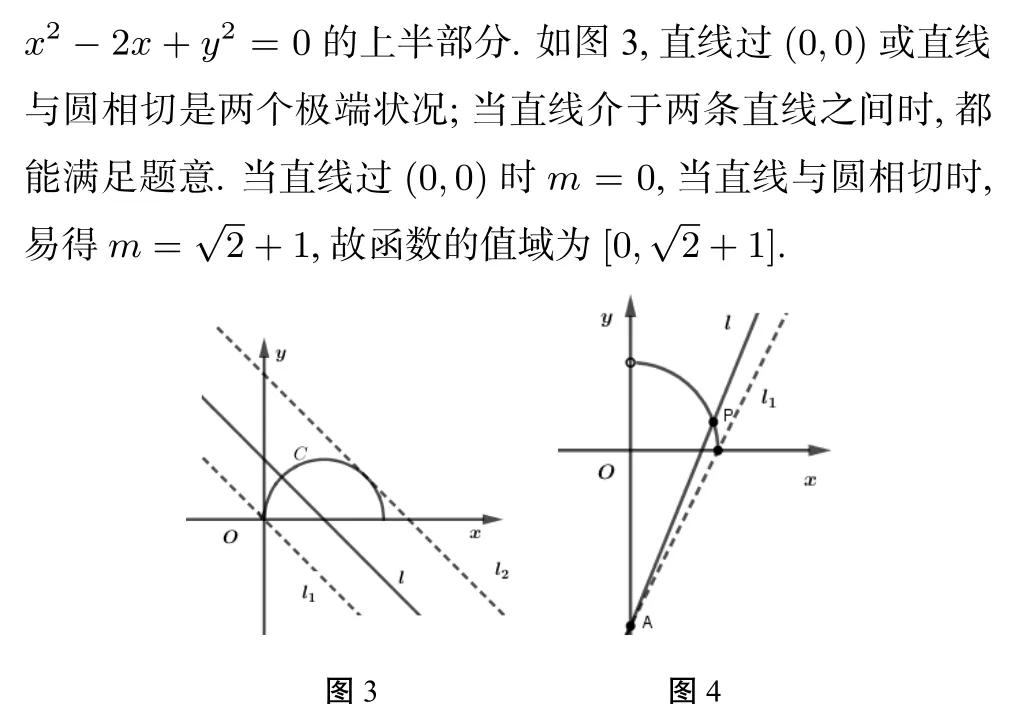
(三)方法總結(jié)

三角換元法和數(shù)形結(jié)合法各有千秋,三角換元法需要對(duì)換元之后的式子再次變形,挖掘幾何意義或進(jìn)行三角恒等變形后利用三角函數(shù)的性質(zhì)求解;而數(shù)形結(jié)合法思路簡(jiǎn)單,最后產(chǎn)生的圖形都是高中生比較熟悉的圓,橢圓,雙曲線;用此種方法更加通用,更加適宜高中生接受和掌握.

由于導(dǎo)數(shù)法求最值和值域是我們?cè)诮虒W(xué)中強(qiáng)調(diào)比較多的并且掌握的比較好,也是求最值和值域的通性通法,我們這里也要加以說(shuō)明.在例1 和例2 中由于函數(shù)的定義域分別為[?1,1]與[0,2],它們分別都是有界閉區(qū)間,而且導(dǎo)函數(shù)也不是太復(fù)雜且極點(diǎn)可以求得,根據(jù)“有界閉區(qū)間上連續(xù)函數(shù)的最值必在極點(diǎn)處或區(qū)間端點(diǎn)處取得”即可以求得函數(shù)值域.而對(duì)于例3 和例4,由于函數(shù)定義域并非有界閉區(qū)間,在用導(dǎo)數(shù)法求值域中可能會(huì)出現(xiàn)需要求極限的情況.

三、教學(xué)思考

(1)滲透數(shù)與形對(duì)立與統(tǒng)一的思想

數(shù)與形是我們?cè)谟懻撘粋€(gè)數(shù)學(xué)對(duì)象必須同時(shí)考慮的兩個(gè)方面.華羅庚先生曾說(shuō)過(guò):數(shù)缺形時(shí)少直觀,形缺數(shù)時(shí)難入微.這是一個(gè)對(duì)數(shù)與形對(duì)立統(tǒng)一的精美概括.在上面討論值域的過(guò)程中,直接用導(dǎo)數(shù)法求值域,就是純粹用代數(shù),在解題中可能遇到困境.而三角換元與轉(zhuǎn)化為方程都很好的體會(huì)到了數(shù)形結(jié)合思想,非常容易理解,而且求解容易.一般而言,直觀的圖形容易找到突破口并且記憶方便,純代數(shù)的方法適用性廣,兩者結(jié)合起來(lái)就更好.

(2)通法與特法在教學(xué)中要并行滲透

在數(shù)學(xué)解題中沒(méi)有一種解法放之四海而皆準(zhǔn),常常我們把適用比較廣的方法稱(chēng)為通用方法,比如導(dǎo)數(shù)法求值域適用性廣,當(dāng)然要重點(diǎn)研究.但是碰到無(wú)理式后,求導(dǎo)比較復(fù)雜,極點(diǎn)難求,另外有時(shí)定義域非有界閉區(qū)間,可能需要求極限,直接求極值難以求得值域.這時(shí)用三角換元,數(shù)形結(jié)合相對(duì)比較簡(jiǎn)單,就可以看作處理這類(lèi)問(wèn)題的特殊方法.特法與通法并行才能加深對(duì)知識(shí)的深層次理解.

(3)在教學(xué)中要注意將特例上升到一般模型來(lái)探究

將特例上升到一般探究符合深度學(xué)習(xí)中的“對(duì)學(xué)習(xí)對(duì)象進(jìn)行深度加工”的特點(diǎn),在前面的拓展中,將學(xué)生遇到的一個(gè)解題困境一般化,抽象出這類(lèi)問(wèn)題的一般模型,提出解決方法,并用典例來(lái)加深理解.提出了這樣一些“有挑戰(zhàn)性”的問(wèn)題,能吸引學(xué)生的學(xué)習(xí)興趣,能提高學(xué)生的數(shù)學(xué)抽象,數(shù)學(xué)建模素養(yǎng).數(shù)學(xué)家波利亞曾指出:當(dāng)你找到一個(gè)蘑菇時(shí),用心觀察,就能找到一堆蘑菇.“抽象,推理,模型”是最重要的三個(gè)數(shù)學(xué)思想,在解題教學(xué)中尤其要強(qiáng)調(diào).

(4)大單元整體教學(xué)的思想

在解題教學(xué)中,學(xué)生常常面臨著“懂而不會(huì)”,“懂一題而不能通一類(lèi)題”的困境,究其原因,是因?yàn)闆](méi)有看清問(wèn)題的全局,只看到了一個(gè)問(wèn)題的某一方面,當(dāng)遷移到另一問(wèn)題時(shí)不能應(yīng)用.古人云:孔子登東山而小魯,登泰山而小天下.大詞人蘇軾在《題西林壁》中感慨“不識(shí)廬山真面目,只緣身在此山中”.這都強(qiáng)調(diào)了,站得高才能看的遠(yuǎn),把握整體才能更好的欣賞把握局部.以求函數(shù)值域?yàn)槔?從整體來(lái)看,基本初等函數(shù)的性質(zhì)以及導(dǎo)數(shù)滲透到各個(gè)角落.但從局部來(lái)看,又有所不同,比如對(duì)于含有指數(shù)函數(shù),對(duì)數(shù)函數(shù),冪函數(shù)的函數(shù)求值域,由于求導(dǎo)簡(jiǎn)單,而且往往具備很好的凸性,導(dǎo)數(shù)法必為首選;對(duì)于無(wú)理函數(shù),求導(dǎo)往往復(fù)雜,這時(shí)對(duì)式子進(jìn)行三角換元或數(shù)形結(jié)合的轉(zhuǎn)化效果會(huì)更佳.