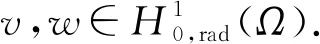一類半正橢圓方程徑向正解的存在性
符 謙
(廣西師范大學(xué) 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院, 廣西 桂林 541006)
1 引言及主要結(jié)果
考慮下列半正橢圓方程徑向正解的存在性與不存在性:
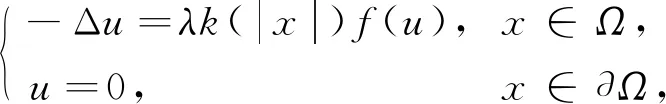
(1)
其中Ω?N(N≥2)是一個(gè)環(huán)A或者單位球B, 參數(shù)λ>0,f∈C([0,∞),)且f(0)<0(半正),k: [a,b]→[0,∞)且k(|x|)不恒為0.此外, 當(dāng)Ω為球時(shí),k為線性映射; 當(dāng)Ω為環(huán)時(shí),k為單調(diào)增函數(shù).環(huán)A和單位球B分別定義為
A∶={x∈N:a<|x| 由于f(0)≠0,k(|x|)不恒為0, 故u(x)恒為0一定不是方程(1)的解.本文總假設(shè)N≥2, 考慮方程(1)的正徑向解, 令r=|x|,u=u(r), 則方程(1)可改寫為 (2) 其中: 當(dāng)Ω為單位球時(shí),a=0,b=1; 當(dāng)Ω為環(huán)時(shí), 0 u(a)=u(b)=0,Ω=A, (3) u′(0)=u(1)=0,Ω=B. (4) 本文總假設(shè): (H1)f∈C([0,∞),)且滿足f(0)<0; (H2) 存在S>0, 使得F(S)>0; (H3) 若F(s)>0, 則f(s)>0; (H5)k: [a,b]→[0,∞)且k(|x|)不恒為0; 此外, 當(dāng)Ω=B時(shí),k為線性映射; 當(dāng)Ω=A時(shí),k為單調(diào)增函數(shù); (H6) 若Ω=B, 則存在常數(shù)p,c>0, 使得|f(s)|≤c(sp+1)(當(dāng)N=2時(shí), 0 此外, 可將條件(H4)減弱為: 條件(H6)表明, 當(dāng)Ω=B時(shí),f(s)在無(wú)窮遠(yuǎn)處具有次臨界增長(zhǎng)階; 條件(H4)強(qiáng)于條件(H7), 條件(H7)強(qiáng)于條件(H8).由條件(H1)和(H2)知,f(s)在(0,∞)上有零點(diǎn), 記f(s)的第一個(gè)(最小的)零點(diǎn)為z, 則有 f(s)<0,s∈[0,z);f(z)=0. (5) 定義 Z∶=sup{s>0:F(t)≤0,t∈[0,s]}. (6) 因此0 F(s)≤0,s∈[0,Z];F(Z)=0; (7) F(s)>0,f(s)>0,s∈(Z,∞). (8) 本文主要結(jié)果如下. 定理1假設(shè)條件(H1),(H5),(H7)成立, 則當(dāng)λ>0充分小時(shí), 方程(1)沒(méi)有非負(fù)解. 定義集合: (9) 其中Ω?N(N≥2)是一個(gè)環(huán)A或者單位球B.定義泛函 (10) 其中: 當(dāng)Ω=B時(shí),a=0,b=1; 當(dāng)Ω=A時(shí), 0 (11) 其邊界條件為: 當(dāng)Ω=B時(shí),v′(0)=v(1)=0; 當(dāng)Ω=A時(shí),v(a)=v(b)=0.定義 (12) 如果f∈C1[0,∞), 則線性化算子L(uλ)的所有第一特征值均非負(fù). 下面除非特殊說(shuō)明, 總假設(shè)條件(H1)~(H6)成立.定義范數(shù)‖u‖p, 其中1≤p≤∞, (14) 任意地固定λ>0, 由式(14)知, 對(duì)?ε>0, 存在一個(gè)常數(shù)M1=M1(ε)>0, 使得 |F(s)|≤εs2+M1,s∈. (15) 由引理1知,i(λ)能由式(12)定義且i(λ)>-∞.如果u∈H*(Ω)且滿足 則稱u是I在H*(Ω)中的極小值點(diǎn).下面尋找I的極小值點(diǎn)u, 并證明其為方程(2)的正徑向解.由于I(0,λ)=0, 因此I的下確界非正.若其下確界為0, 則其極小值點(diǎn)可能是u恒為0, 但其并不是方程(2)的解, 故其下確界是負(fù)的. 證明: 首先證明存在一個(gè)函數(shù)V(x)滿足V∈H*(Ω),V(r)不恒為0, 且 (17) 引理3若i(λ)<0, 則當(dāng)λ′>λ時(shí),i(λ′)<0. 證明: 令i(λ)<0, 則存在一點(diǎn)u∈H*(Ω), 使得I(u,λ)<0, 即 因此 當(dāng)λ′>λ時(shí), 有 即i(λ′)≤I(u,λ′) 引理4假設(shè)條件(H1),(H8)成立, 則存在一個(gè)λ1>0, 使得當(dāng)λ∈(0,λ1)時(shí), 有I(u,λ)≥0(u∈H*(Ω)),i(λ)=0. 證明: 由于f(0)<0, 則對(duì)較小的s>0, 存在常數(shù)c>0, 使得F(s)≤-cs, 結(jié)合條件(H8)知, 存在常數(shù)M3=M3(s)>0, 使得F(s)≤M3s2(s≥0), 再結(jié)合條件(H5)可得 定義 λ*∶=inf{λ>0:i(λ)<0}. (18) 由引理2~引理4知,λ*>0. 引理5[12]當(dāng)λ≤λ*時(shí),i(λ)=0; 當(dāng)λ>λ*時(shí),i(λ)<0. 定理3若λ>λ*, 則I(·,λ) 在H*(Ω)中存在極小值點(diǎn). 證明: 若λ>λ*, 則由引理5知i(λ)<0.由引理1知,I(·,λ)在H*(Ω)中有下界且其下確界是負(fù)的.定義 |F(s)|≤C(s2+1),s∈. 因此F(vn)的積分收斂到F(v0)的積分[21], 即 (19) 結(jié)合I(u)的定義和I(vn)→I0及式(19), 知 其中I0是I(u)的下確界.表明 (20) 因?yàn)樵贖*(Ω)中vn?v0, 所以 (21) 雖然找到了I(·,λ)在H*(Ω)中的極小值點(diǎn), 但并不能確定其是否為I(·,λ)的一個(gè)臨界點(diǎn).對(duì)于極小值點(diǎn)u, 令h(t)∶=I(u+tv,λ), 其中v∈H*(Ω)為任意的試驗(yàn)函數(shù).由于u是一個(gè)極小值點(diǎn), 則對(duì)于t≥0, 有h(0)≤h(t), 因此h′(0)≥0.若對(duì)于一個(gè)較小的ε>0, 有 h(0)≤h(t),t∈(-ε,ε), (22) 則h′(0)=0且u為I的一個(gè)臨界點(diǎn). 對(duì)于a≤ri-1 (23) (24) 當(dāng)λ>λ*時(shí), 由引理5知,i(λ)<0.由定理3知,I(·,λ)在H*(Ω)中有極小值點(diǎn). 引理7若λ*≤λ<∞且u是I(·,λ)在H*(Ω)中的極小值點(diǎn), 滿足u不恒為0, 則有: 1) 存在r∈(a,b), 使得u(r)>Z; 2) 若存在a≤r1≤r2≤b, 使得u(r1)=u(r2)=0,u(r)>0(r∈(r1,r2)), 則存在r3∈(r1,r2), 使得u(r3)>Z. 證明: 當(dāng)λ>λ*時(shí),I(u,λ)=i(λ)<0, 顯然u不恒為0; 而當(dāng)λ=λ*時(shí),i(λ*)=0, 極小值點(diǎn)可能是u恒為0, 而題設(shè)條件排除了這樣的極小值點(diǎn). 1) 用反證法.假設(shè)對(duì)?r∈(a,b), 有u(r)≤Z, 則F(u(r))≤0.由于u(r)不恒為0, 因此u′(r)不恒為0.又因?yàn)?≤k(r)≤M2, 故I(u,λ)>0.這與I(u,λ)=i(λ)≤0矛盾, 故1)成立. 2) 假設(shè)u(r1)=u(r2)=0,u(r)>0(r∈(r1,r2)).用反證法.若對(duì)?r∈(r1,r2),u(r)≤Z, 則F(u(r))≤0, 由于u′(r) 不恒為0, 0≤k(r)≤M2, 故有 定義當(dāng)r∈[a,b](r1,r2)時(shí),v(r)∶=u(r); 當(dāng)r∈(r1,r2)時(shí),v(r)∶=0, 則v∈H*(Ω), 且 I(v;r1,r2)=0,I(v;a,r1)=I(u;a,r1),I(v;r2,b)=I(u;r2,b). 由式(24)知, 這與u是I(·,λ)在H*(Ω)中的極小值點(diǎn)矛盾, 故存在r3∈(r1,r2), 使得u(r3)>Z.證畢. 引理8若λ*≤λ<∞且u是I(·,λ)在H*(Ω)中的極小值點(diǎn), 滿足u不恒為0, 則存在一串序列tn∈(a,b), 使得u(tn)>0且tn→b(n→∞).若Ω=A, 則存在一串序列sn∈(a,b), 使得u(sn)>0且sn→a(n→∞). 證明: 令Ω=B, 則a=0,b=1, 證明存在序列tn∈(0,1), 使得u(tn)>0,tn→1(n→∞). 用反證法.假設(shè)tn不存在, 則對(duì)任意固定的δ∈(0,1), 有u(r)恒為0(r∈[δ,1]).定義v(r)∶=u(δr)(r∈[0,1]), 顯然v∈H*(B).利用變量代換s=δr, 并結(jié)合條件(H5), 計(jì)算 令 則有I(v)=h(δ)且I(u)=h(1)=P-Q.由于I(u)=i(λ)≤0, 因此有P≤Q, 由于u不恒為0, 所以P>0.對(duì)于t∈(0,1], 當(dāng)N=2時(shí),h(t)=P-Qt-3,h′(t)=3Qt-4>0; 當(dāng)N≥3時(shí), 因此h(t)在(0,1]上遞增, 且有I(v)=h(δ) 令Ω=A, 證明存在序列tn∈(a,b), 使得u(tn)>0且tn→b(n→∞).用反證法.假設(shè)對(duì)任意固定的δ∈(0,1), 有u(r)恒為0(r∈[δb,b]).延拓u(r), 令u(r)恒為0(r∈[a,b]).定義v(r)∶=u(δr)(r∈[a,b]), 則v(a)=v(b)=0且v∈H*(A).余下證明與Ω=B情形相同, 故略.從而存在序列tn∈(a,b), 使得u(tn)>0且tn→b(n→∞). 當(dāng)Ω=A時(shí), 證明存在序列sn∈(a,b), 使得u(sn)>0且sn→a(n→∞).用反證法.假設(shè)對(duì)某個(gè)r0>a, 有u(r)恒為0(r∈[a,r0]), 由引理7中1)知, 存在一個(gè)點(diǎn)r1, 使得r0 v(r)∶=u(r-a+r0)(r∈[a,a1]),v(r)∶=Z(r∈[a1,r1]),v(r)∶=u(r)(r∈[r1,b]), 則v∈H*(A).利用變量代換t=r-a+r0, 有 由于當(dāng)t∈[r0,r1]時(shí),F(u(t))≤0且F(u(t))不恒為0,u′(t)不恒為0, 0≤k(t)≤M2, 因此被積函數(shù)是正的.又因?yàn)閗(r)單調(diào)遞增, 所以 由于I(v;a1,r1)=0,I(u;a,r0)=0,I(v;r1,b)=I(u;r1,b), 因此有 矛盾, 故存在一串序列sn∈(a,b), 使得u(sn)>0且sn→a(n→∞).證畢. 引理9[12]令λ*≤λ<∞且u是I(·,λ)在H*(Ω)中的極小值點(diǎn), 滿足u不恒為0.則當(dāng)Ω=B時(shí),u(r)>0(r∈(0,1)); 當(dāng)Ω=A時(shí),u(r)>0(r∈(a,b)). 若Ω?N(N≥2)是一個(gè)環(huán)或單位球, 則由f(0)<0及條件(H7)知, 存在M4=M4(s)>0, 使得f(s)≤M4s(s≥0).由條件(H5)知, 存在M2=M2(Ω)>0, 使得0≤k(|x|)≤M2.用反證法.假設(shè)當(dāng)λ>0充分小時(shí),u是方程(1)的一個(gè)非負(fù)解.令μ1是-Δ帶有Dirichlet邊界條件的第一特征值, 且φ是其對(duì)應(yīng)的特征函數(shù), 滿足φ(x)>0, 則有 -Δu=λk(|x|)f(u)≤λM2M4u, (25) 將式(25)兩邊與φ做L2內(nèi)積, 得 μ1(u,φ)L2≤λM2M4(u,φ)L2, 定理4令λ>λ*且uλ是I(·,λ)在H*(Ω)中的極小值點(diǎn), 則其為方程(2)的一個(gè)正解, 且屬于C2[a,b]并滿足I(uλ,λ)=i(λ)<0. 故u是方程(2)的一個(gè)弱解.當(dāng)Ω=B時(shí), 由橢圓正則性理論及假設(shè)條件(H6), 可得u∈W2,q(Ω)(?q∈[1,∞)); 當(dāng)Ω=A時(shí), 由引理6知,u∈C1/2[a,b], 結(jié)合橢圓正則性理論可知,u∈W2,q(Ω)(?q∈[1,∞)).此外, 由于方程(2)是一個(gè)常微分方程, 且f(u(r))∈C[a,b], 則u∈C2[a,b].證畢. 定理5對(duì)于λ=λ*, 方程(2)有一個(gè)正解u*(u*∈C2[a,b]), 且滿足I(u*,λ*)=i(λ*)=0. 證明: 令λn是一串序列,λn>λ*且λn→λ*(n→∞).設(shè)un是由定理4得到的相應(yīng)λ=λn的極小值點(diǎn).由于I(un,λn)<0, 因此 結(jié)合式(15)及0≤k(r)≤M2, 有 當(dāng)n→∞, 有 因此,u*是方程(2)的弱解, 再結(jié)合定理4的證明過(guò)程, 可得u*∈C2[a,b].由于un是相應(yīng)λ=λn的極小值點(diǎn), 因此有I(un,λn)≤I(v,λn)(v∈H*(Ω)).當(dāng)n→∞時(shí), 有I(u*,λ*)≤I(v,λ*), 因此u*是I(·,λ*)的極小值點(diǎn), 即I(u*,λ*)=i(λ*)=0.由于u*是方程(2)的解且u*不恒為0, 再結(jié)合引理9和引理10知,u*在Ω中嚴(yán)格正.證畢. 若f∈C1[0,∞), 下面證明線性化算子L(uλ)的所有第一特征值均非負(fù).固定λ∈[λ*,∞), 令u=uλ, 則二階導(dǎo)數(shù)I″(u)具有雙線性形式






2 極小值點(diǎn)的存在性




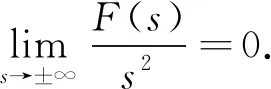

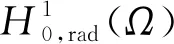







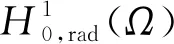

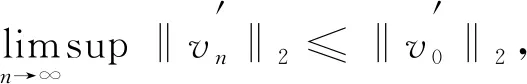

3 極小值點(diǎn)的性質(zhì)
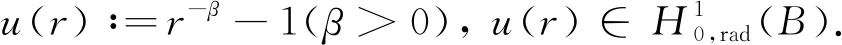


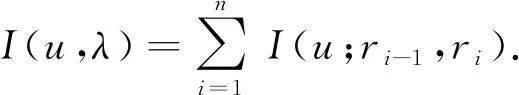
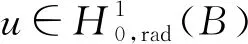
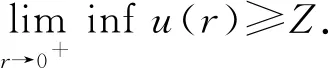


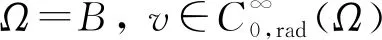
4 主要結(jié)果的證明
4.1 定理1的證明
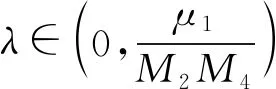



4.2 定理2的證明