Xi Zhao(趙曦) Gangtai Zhang(張剛臺) Tingting Bai(白婷婷)Jun Wang(王俊) and Wei-Wei Yu(于偉威)

1School of Physics and Information Technology,Shaanxi Normal University,Xi’an 710062,China

2College of Physics and Optoelectronics Technology,Baoji University of Arts and Sciences,Baoji 721016,China

3College of Mathematics and Information Science,Baoji University of Arts and Sciences,Baoji 721013,China

4Institute of Atomic and Molecular Physics,Jilin University,Changchun 130012,China

5Department of Physics,Kansas State University,Manhattan,KS 66506,USA

6School of Physics and Electronics,Qiannan Normal College for Nationalities,Duyun 558000,China

7School of Physics and Electronic Technology,Liaoning Normal University,Dalian 116029,China

Keywords: strong field physics,TDSE,OPENACC,GPU,electron correlation,helium

1. Introduction

The rapid development in laser technologies opens a way for scientists to probe and even control the fundamental dynamics of electron correlations.[1-21]As the simplest multi-electron atom, helium is an idea starting point for exploring electron correlation dynamics in multi-electron systerms.[14,25-41]However,due to its six degrees of freedom,the response of helium to strong fields is considerably more complicated than that of single-electron atoms, which poses great theoretical and computational challenge. To overcome this difficulty, a set of conventional CPU parallel computing techniques have been developed to numerically solve the time-dependent Schr¨odinger equation(TDSE)of helium subjected to a laser pulse. Penget al.investigated the electron correlation effects in two-photon-double-ionization(TPDI)of helium by the finite-element-discrete-variable-representation(FEDVR) method.[39]Parkeret al.used the finite-difference method to calculate the above-threshold ionization (ATI)process.[40]Pirauxet al.investigated the electron correlation effect using the Gauss-Sturman function.[30]All of these simulations are very likely a numerical virtual experiment on the servers (about 200 to 1000 CPU cores are used in Refs. [39,40]). Thus, more efficient algorithm is needed to further promote the numerical simulations of helium (and even more complex multi-electron systems beyond helium)in strong laser field investigations. One of the potential solution is the graphic processing unit(GPU)programming,which is the most powerful high performance computing tool so far and widely applied in both science and engineering numerical studies.[43-50]

GPU contains hundreds of computing cores and is originally designed for highly parallel process of graphic rendering.[43,44]Compared with CPU, the computing performance of GPU can be increased by tens of times with proper optimizing.[43-50]To do this, a so-called “Compute Unified Device Architecture (CUDA)” GPU programming model is present.[44]However,porting of legacy CPU-based codes with CUDA often necessitates explicit compute and data management, thus requiring significant structural changes to existing applications.[45]Therefore, we make the choice to use OpenACC, which gives an alternative model as a GPU programming scheme.[51]OpenACC is a set of directive-based extensions to C,C++and Fortran that allow programmers to annotate regions of code and data for offloading from a CPU host to an attached GPU,without requiring modification to the underlying CPU code itself. Programmers simply insert OpenACC directives before specific code sections to engage the GPU to accelerate the code. This approach enables the compiler to target and optimize parallelism automatically. More example programs and detailed description of openACC can be found in openACC official website.[51]

In this work, we present a GPU based openACC fortran program HeTDSE,which is an efficient tool to investigate the non-perturbative electronic dynamics of helium subjected to a strong laser pulse by solving full-dimensional two-electron TDSE. It goes beyond the single-electron-approximation(SEA) approach and includes the response to the field of all two electrons. To build helium wavefunction, B-spline basis sets, which were widely used in computational atomic and molecular physics,[21,52-62]are used to construct the radial part of the wavefunction,while spherical harmonic functions are used to express for the angular part. The reason why we use B-spline basis sets to expand helium radial wavefunction is that B-spline function has great advantages of describing both bound and continue states with small number basis sets.[52,53,55]Adams algorithm is employed for the time propagation.[63]Another advantage of using B-spline basis sets and Adams method is that it is easy to parallelize the code and will get an excellent paralleling scaling with openACC.

The rest of this paper is organized as follows: In Section 2,we present the theoretical background on HeTDSE.In Section 3 we exhibit an overview of the package structure, the input,output files and the code parallelizing. In Section 4 we show several test applications of HeTDSE. The parallel efficiency is given in Section 5. We present our conclusions in Section 6. Atomic units are used throughout, unless stated otherwise.

2. Mathematical setup and algorithm

2.1. B-spline function

B-splines are functions designed to generalize polynomials for the purpose of approximating arbitrary functions, we use B-spline basis sets to construct the helium wavefunction in HeTDSE.Thus,we begin this section with a brief description of B-spline function,very details of B-spline function can be found in Ref.[55].

A B-spline function is defined by the orderkand a set of the breakpoints{tj},

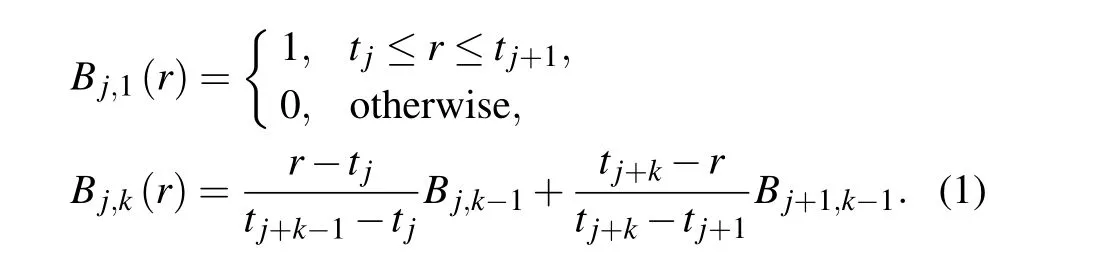
This sequence tends to a linear sequence asγ →0 while all points exponentially accumulate close torminasγ →∞.

The third is a linear-parabolic sequence. A useful sequence adapted to a good description of both the bound and the continuum states associates to a linear spreading at large distances with a quadratic sequence close to the origin.[55]

The B-spline function orderk=7 is used throughout this work, so we do not write outkin B-spline functions for simplification.

2.2. Time independent Schr¨odinger equation

The helium eigenstateφn(r1,r2) and its corresponding eigenvalueEnis the solution to the time-independent Schr¨odinger Eq.(TISE)of helium:

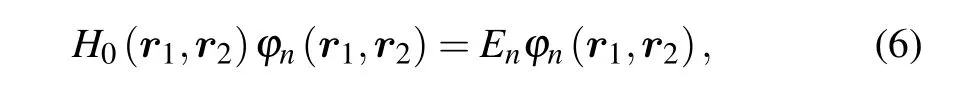
withH0(r1,r2)being the laser-free Hamiltonian

whereNis the number of the B-spline basis sets for each timeindependent wavefunctionφn(r1,r2),l1(l2) denotes the angular momenta for electron 1(2),Lis the total orbital angular momentum,Mis itsz-component,Sis the total spin,{ci}is the expansion coefficient, and eachicorresponds to a set of{n1,l1,n2,l2}. Coupled spherical harmonic functions are used to express for the angular part of the time-independent wavefunction:

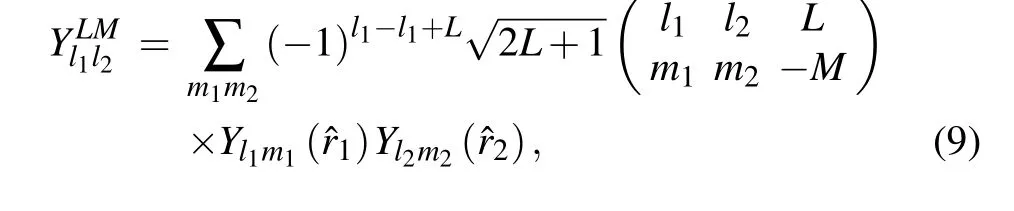
wherem1(m2)is thez-component ofl1(l2),andYlm(?r)is usual spherical harmonic functions.

The wavefunctionφn(r1,r2), eigenvalueEnas well as the expansion coefficient{ci}in Eq. (8) can be obtained by directly diagonalizing Eq. (6). For this purpose, there are a set of matrix integrals that would be performed: the kinetic energy integral matrix element

Ki j,PijandOi jare straightforward to discretize and to be calculated. However,the calculation ofCi jis different. To calculateCijwe expand the electron-electron correlation term in a truncated multipole series:

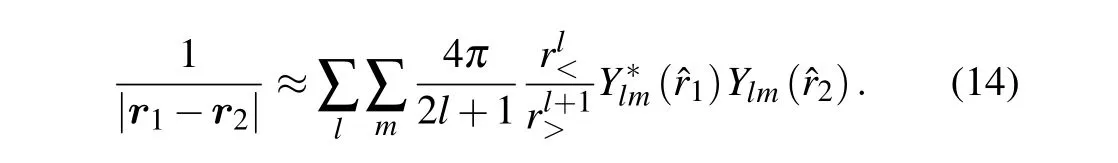
Thus, each of the terms is handled in a similar manner to the one-electron operators.[53]In HeTDSE, all the integrals are carried by the Gauss-Lagrange integration method,which has been widely used in other works.[41]

2.3. The time-dependent Schr¨odinger equation

We solve the helium TDSE within the dipole approximation and length gauge. The full-dimension TDSE of helium can be written as

Here ?εis the laser polarization direction,ωandφare the frequency and the carrier envelope phase,respectively; andf(t)is the temporal envelope.

The total time-dependent wavefunctionΨ(r1,r2,t) can be expanded in terms of the field-free atomic eigenfunctions:

which can be solved with the Adams method. Details of this algorithm can be found in Ref. [63]. The energy differenceEmn=Em-Enand the transition dipole element between〈φn(r1,r2)|and|φm(r1,r2)〉,

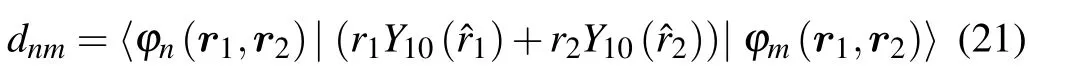
can be calculated from the solution to Eq.(6).

2.4. Absorbing boundary

An absorbing layerA(r1,r2) is used to smoothly bring down the wavefunction and to prevent the unphysical reflection from the boundary. The absorbing function has the following form:

Thus,there are two interpretations of the ionization yield.First,we directly calculate the single(double)ionization yield by summing all the possibilities of the wavefunction with an eigenvalue larger than-2.0(0.0):

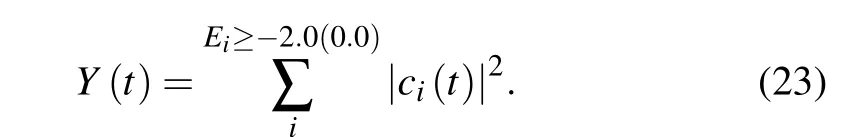
Alternatively,the ionization probability is calculated by

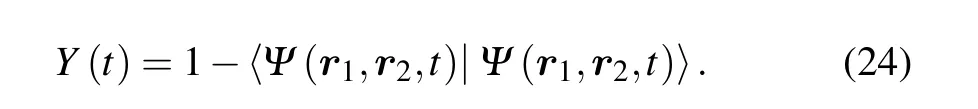
Although we have used an absorbing to avoid the nonphysical reflecting,the simulation box still needs to be set big enough so that the physical system is not perturbed by the absorbing boundaries.

3. Description of the package

HeTDSE code package contains 9 fortran files and 4 input files. The fortran driver programs,functions,subroutines,input and output files are all introduced briefly in this section.

3.1. Fortran program files

These fortran codes should be run one by one: Firstly,runningeigen-equation.fto solve Eq. (6) to get wavefunctionφn(r1,r2), eigenvalueEnas well as the expansion coefficient{ci}. Then, with the output files ofeigenequation.f,runningdipole.f90to get the transition dipoles element〈φn(r1,r2)|(r1Y10(?r1)+r2Y10(?r2))|φm(r1,r2)〉. Next,runningmatrix.f90to prepare input files fortdse.f90. Finally,runningtdse.f90to solve Eq. (20) to get the time-dependent wavefunctionΨ(r1,r2,t).

There are other five fortran programsorder.f,rsg.f,wig.f,angl16.f90andSUBROUTINE.f90in HeTDSE. These five programs are the ”support codes”, we DO NOT suggest the users to modulate them.

3.2. Lower-level functions and subroutines

The lower-level functions and subroutines in this program are:

PREQUAN: Get the index of the one electron functionsBn(r)Ylmfrom 1 ton×(lmax+1).

QUAN2012: Select the basis sets that satisfies physics considerations: the one electron angular momental1,l2should satisfy|l1-l2|≤L ≤|l1+l2| and the wavefunctionΨ(r1,r2)/=0.

gauleg: Calculate the Gauss-Lagrange integration.

DBSP2: Calculate the second derivative of the B-spline function d2Bn(r)/dr2.

DBSP1:Calculate the first derivative of the B-spline function dBn(r)/dr.

RKTSQ:Set the breakpoints distribution.

Bspline2006: Calculate the B-spline functionBn(r).

SingleInteg2012: Calculate the integrationPij,KijorOij.

DmultiInteg2012:Calculate the electron-electron integrationCij.

HAMILTON2012: Construct the Hamiltonian.

RSG: Diagonalize the matrix, get the energy level and wavefunctions.

ANG: Calculate the angle part of transition dipole element.

3.3. Input files

There are totally four input files in HeTDSE,eigenequation.input,dipole.input,matrix.inputandtdse.input,which contain input parameters used byeigne-equation.f,dipole.f90,matrix.f90andtdse.f90, respectively. In this subsection,we present how to set these parameters in these input files one by one.

Eigen-equation.input

Line 1: Set total angular momentumLin Eq.(8).

Line 2: Set total spin in Eq.(8).

Line 3: Set max angular momentum for each electron

lmax.

Line 4: Set the order of the B-spline functionk.

Line 5: Set number of B-SPLINE function breakpoints,that is to say,nin Eqs.(2),(3),and(4).

Line 6:Set total number of the basis sets for the He wavefunctionNin Eq.(8).

Line 7:i0in Eq.(4).

Line 8: Set the simulation box size in radial direction,rmax.

Dipole.input

Line 1:Set total angular momentumLof〈φn(r1,r2)|and|φm(r1,r2)〉in Eq.(8),respectively.

Line 2: Set total spinMof〈φn(r1,r2)|and|φm(r1,r2)〉in Eq.(8),respectively.

Lines 3-8 indipole.inputare the same as lines 3-8 in

eigen-equation.input.

Matrix.input

First values in lines 1,2,3 and 4: The numbers of the basis sets used in TDSE of states areL=0,L=1,L=2,L=3 andL=4,respectively.

Second values in lines 1, 2, 3 and 4: The total numbers of the basis sets of states areL=0,L=1,L=2,L=3 andL=4,respectively.

The default max total angular momentum isL=4,larger total angular momentums can be added in this input file, if needed.

Tdse.input

User should not change lines 1 and 2 intdse.input,so we skip them and begin with line 3.

Line 3:The maximum number of time steps allowed.Default value is 600000.

Line 4: Frequency of the electric field in atomic unit.

Line 5: Number of the laser cycles.

Line 6: Intensity of the electronic laser field in atomic unit.

Line 7: Relative and absolute errors. Default values are 10-7and 10-7,respectively.

3.4. Output files

Output files of eigen-equation.f:

There are two output files after runningeigen-equation.f:the coefficientci(i=1,...,N)of the wavefunctionφn(r1,r2),and the eigenvalueEn.

1.S.dat: This file stores the coefficientciin Eq.(6). The file name would change toP.dat,D.dat,F.datandG.datifL=1,2,3,4,respectively.

2.OMEGA-S.dat: This file stores the eigenvalueEnof states withφn(r1,r2). The file name would change toOMEGA-P.dat,OMEGA-D.dat,OMEGA-F.dat,OMEGAG.datifL=1,2,3,4,respectively.

Output files of dipole.f90

There is one output file after runningdipole.f90: the transition dipole moment elements between a pair of states with neighbouring total angular momentumsLandL+1.

Output files of matrix.f90:

There are three output files after runningmatrix.f90:

1.eigenval.out: This file stores all the eigenvalues in the orderL=0,1,2,3,4.

2.HI.dat: This files stores all the dipole matrix elements.

3.OMEGA.dat: This files stores all the energy differences.

Output files of tdse.f90

There are four output files after runningtdse.f90:1.laser.dat: This file stores laser fieldE(t).

2.single-ion.dat: This file stores the single ionization yieldIs(t).

3.double-ion.dat: This file stores the double ionization yieldId(t).

4.c.dat: This file stores the solutionan(t) (n=1,...,Ntotal)to the coupled partial differential equation(20)at each time step.In principle,if we obtainan(t),all the physical information can be retrieved.

3.5. OpenACC parallelizing implementation

In this subsection, we detailedly explain the OpenACC implementation in HeTDSE.In HeTDSE package,more than 99% computation time would be paid to calculate transition dipole momentdmnand time propagation. Thus,we focus on accelerating the two calculations with openACC.Indipole.f90programs, four do-loops are needed to get all the transition dipole moment elementsdmn(see Eq. (21) for mathematical expression),and each loop would run 2000-10000 times. The code and corresponding openACC accelerated implementation is shown below:

Although the computing scale is large, the code structure itself is really simple(nothing but a sum calculation)and openACC can achieve a high performance parallelizing scaling. All four do-loops are parallelized directly by inserting the OpenACC directive “!$ACC KERNELS”, then the data transfer between the host and the GPU memory is automatically executed. The calculation in the area (line 2 to line 12)of directive is executed and accelerated on GPU.Optimization for time propagation is similar, here is the Adams time propagation code at each time step and corresponding openACC accelerated implementation:

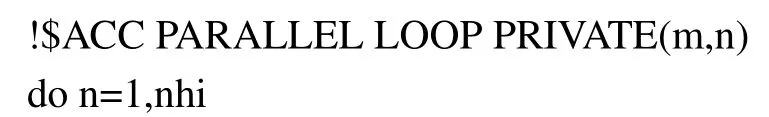
As we know,the data transfer between the host and GPU memory affects the computational time. To further minimize the cost of data transfer,we use the OpenACC“DATA COPY”before time propagating starts,and“END DATA”is used to release the GPU memory at the end of time propagating:

The datacopy (namelist) is the directive that copies the data from host to GPU memory,then data on GPU memory is used without the data transfer back and forth between the host and GPU every time step. Clearly, by inserting datacopy, the calculational time is much saved.

The advantages of using B-spline basis set and Adams method in HeTDSE are emphasized again at the end of this section: First, it is convenient to implement openACC. Second, the parallelizing scaling has a high performance, which will be shown in Section 5.

4. Sample results

In order to verify the accuracy of our program, we compare our results with previous literatures. In the calculations,the radius of the cavity isrmax=70,rmin=0 for both electrons and it is described by 30 B-spline functions of order 7.We useli=1,2=0,1,2,3,4 andL=0,1,2,3,4 in below simulation examples. Linear-parabolic breakpoints sequence is chosen. Total number of basis setsNtotal=11000 are used during the time-dependent simulations.rmaskin absorbing boundary is set tormask=60. It should mention here that choosing such parameters is because we can get a convergence in the ionization calculation in Subsection 4.3. For the other calculations,such as ground/bound states calculations and excited states dynamics simulations,we do not need to use a radius as large as 70.

4.1. Ground and bound states calculation of helium

In Table 1, we show the eigenvalues of few low bound states for different total angular momenta. Table 1 shows that,for all the calculated levels, at least the accuracy up to two digits after the decimal point has been obtained. Specifically,we compare our ground state eigenvalue with a more accurate method from Ref. [22]. In Ref. [22], Kinoshita used 39 parameters and finally obtained a eignvalue of-2.9037225,which is only 0.0036935 of difference from our result. This small difference indicates that the accuracy from our method is acceptable.

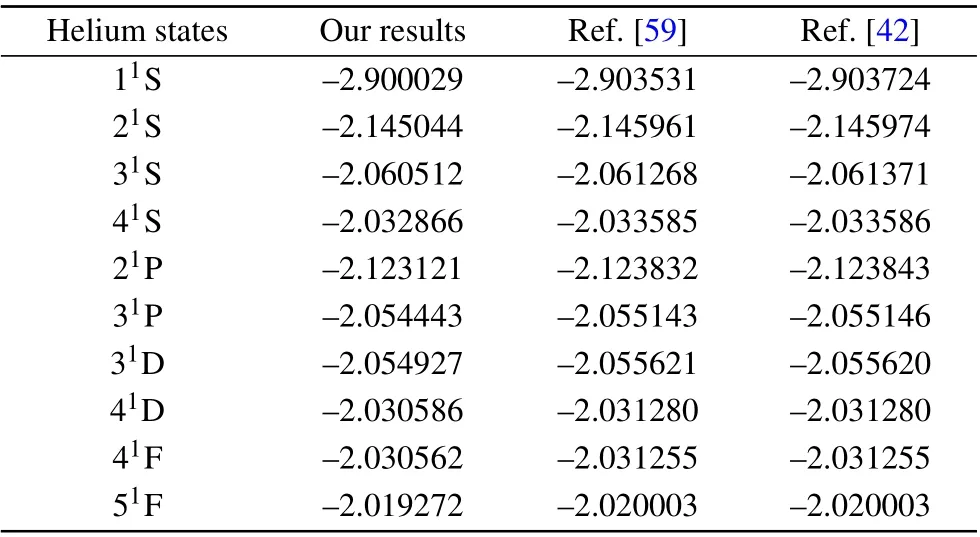
Table 1. The energy level of some bound states.

Fig.1. The density distributions of some bound states in coordinate space.

The effects of two-electron correlation coming from electron-electron repulsion have been a important subject from the early days of quantum mechanics,the relative positionr12of two electrons are even more important than their absolute positions for some purposes. Thus it is necessary to reduce the two-electron density further. The first specific calculation in respect of this was performed by Coulson and Neilson who deduced the expression for the distribution function of the interelectronic distancer12,[23]

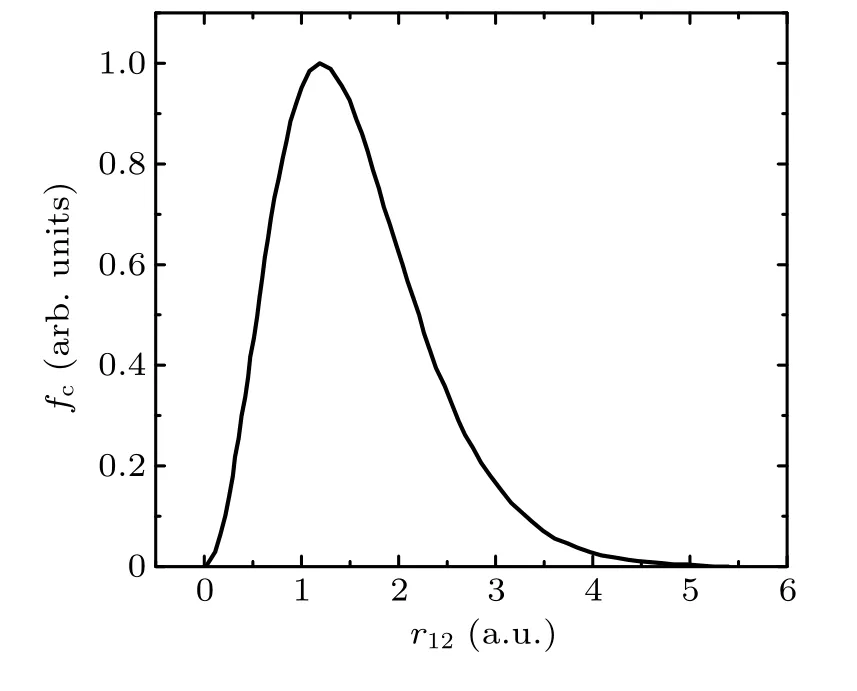
Fig.2. The intracule density fc(r12)as a function of r12.

4.2. Excited states dynamics

Now we turn to the second example: excited states dynamics. We focus on the carrier-envelope phase (CEP) effect on band-band state transition induced by a laser pulse.The CEP is a crucial parameter in describing the characteristics of a laser pulse, we can control the dynamic process of matter-laser interaction by measuring or adjusting the CEP.[64-69]Especially, the CEP effect on the bound-bound transition of an atom has been investigated theoretically and experimentally.[64-69]Here we try to reproduce the result from Ref.[67]. In Ref.[67],the authors used Hylleraas coordinates to reconstruct the wavefunction of helium,and they introduced a parameterMto quantify the CEP effect:

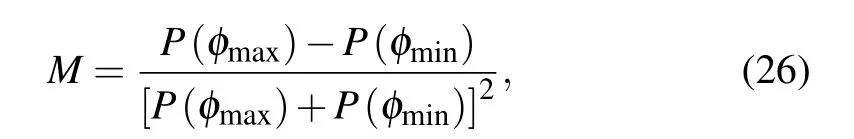
whereP(φmax) andP(φmin) are, respectively, the maximum and minimum populations for a given excited state. A large value ofMcorresponds to a strong CEP effect. In this simulation,the laser parameters are the same as those in Ref.[67].We use HeTDSE to obtain the valueMfor1Dstate after the laser ends, as shown in Fig 3. Our result matches well with that in Fig.1(b)from Ref.[67].

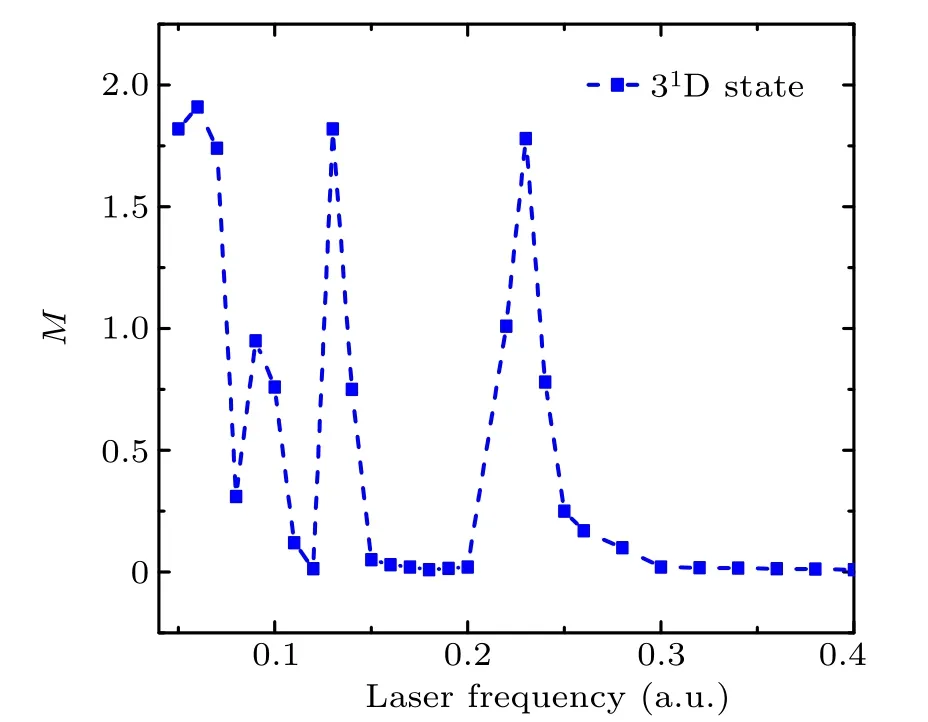
Fig. 3. The CEP parameter M vs the laser frequency for 31D state of helium.

4.3. Excitation and ionization yields

Next, we calculate the excitation and ionization yields of helium in a strong laser pulse. Our basis sets covers the energy range located beyond the double-ionization threshold. The initial state is the ground state of helium1S2〉.The laser pulse has a duration of 3.8 fs and the peak intensity of 2.97×1014W/cm2, which is the same as those in Refs.[54,59]. The present results in Fig.4 are accordant with the data from Hasbani[54]and Scrinzi,[59]which certifies the accuracy of our code.

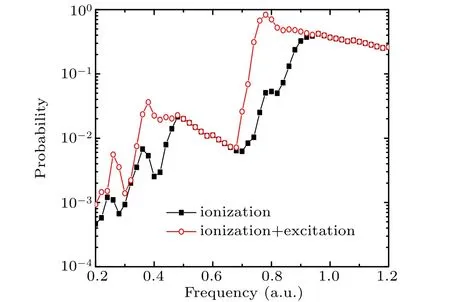
Fig. 4. Excitation and ionization probabilities, for the helium atom,with a pulse duration of 3.8 fs (fixed) and a peak intensity of 2.96×1014 W/cm2.

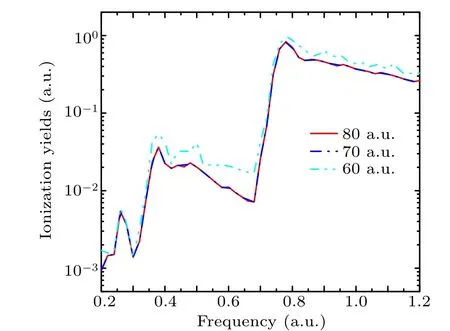
Fig.5. Ionization yields for different simulation box R=80(red line),70(blue dotted line),and 60(cyan dotted line),for the helium atom,the laser parameters are the same as those in Fig.4.

The convergence of the radius is checked in Fig. 5. In Fig.5,we choose three different simulation boxesrmax=80,rmax=70 andrmax=60,the absorbing boundary is set to 70,60 and 50, respectively. In Fig. 5, we can see that ionization yields fromrmax=80 andrmax=70 are almost same,in the meantime, the ionization yields fromrmax=60 are much larger than those in thermax=80 andrmax=70 cases. This result indicate that under such laser parameters,we can obtain a convergence with the radius equal to 70.

4.4. Electrons wavepacket dynamics

Using the time-dependent wave function,the density distribution of the electrons in coordinate space can be obtained by

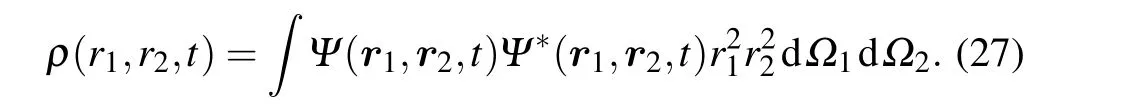
HereΩ1(2)is the angular part of the electron 1(2). The density distribution of continuous states in coordinate space is shown in Fig.6(a)at the timeTend(which is labeled in Fig.6(b)). We can see that there are evident single ionization characteristics from this figure.

Once the wavefunction at timetis obtained,we can also calculate the momentum distribution of the wavefunction with momentumk1andk2by Fourier transform

,In order to check the accuracy of our code,we employ a twocolor laser field with an intensity ofI=1.0×1012W/cm2,the central energies are 36 eV and 80 eV,respectively, we calculate the momentum distribution after the laser ends in Fig. 7,the result coincides with the result from Ref.[21].

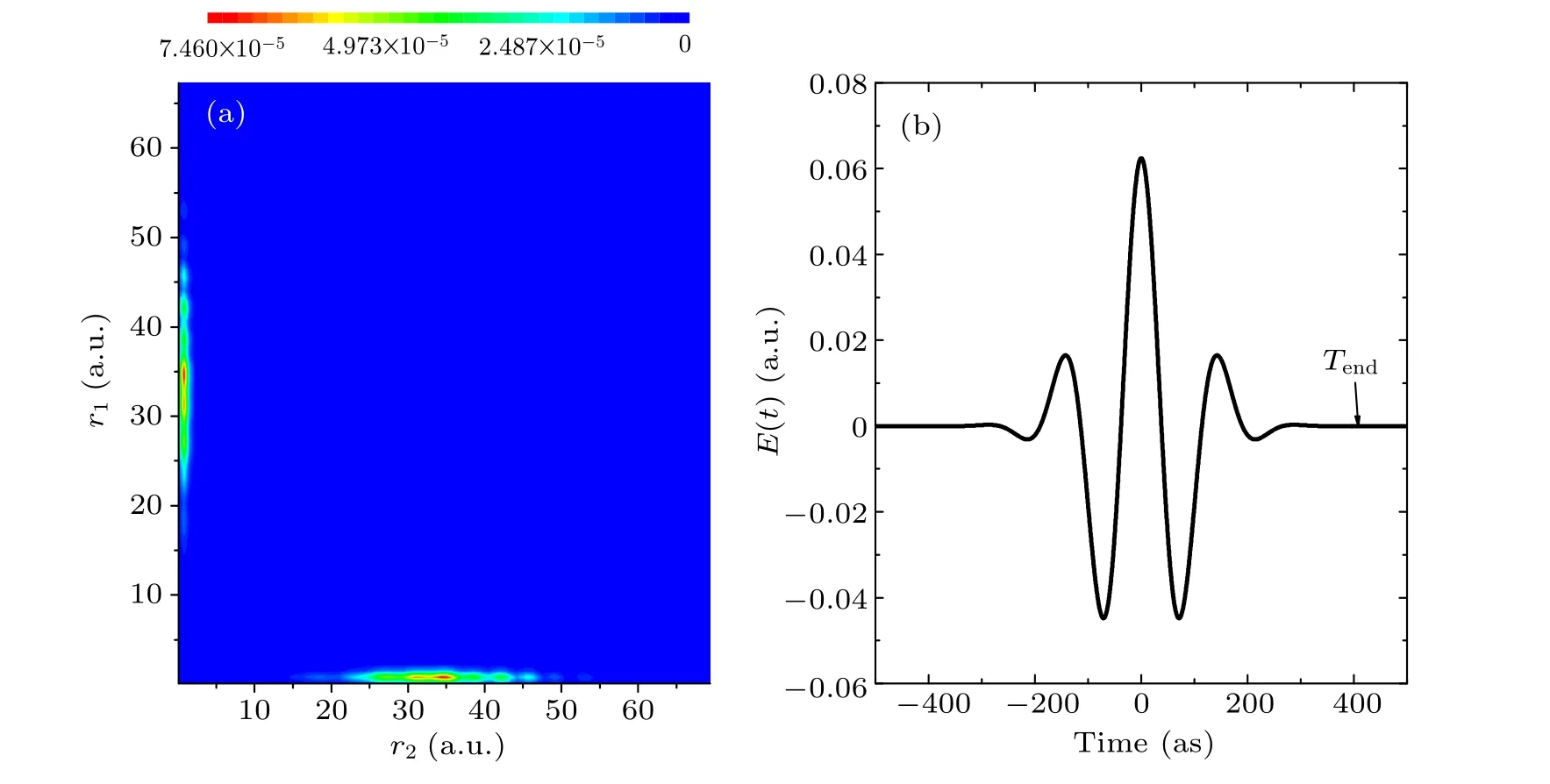
Fig.6. The distributions of the continuum state in the coordinate space ω =1.0,FWHM=2 OC,intensity I=1.0×1013 W/cm2 when the laser is ended.

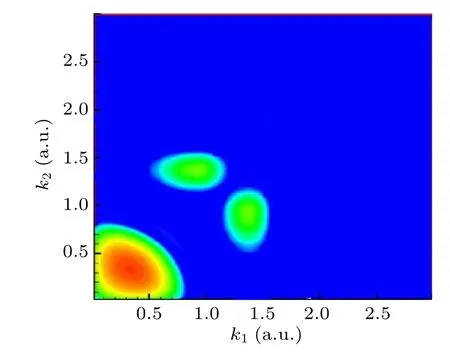
Fig. 7. The two-electron momentum distribution. We use a two-color laser field,in which the central energies are 36 eV and 80 eV,both the intensities are I=1.0×1012 W/cm2.

5. Parallel scaling

To test the parallel efficiency of HeTDSE, we compare the serial CPU program(runs at Intel xeon E5-2640 CPU with 2.5GHz clock speed and 15MB L3 cache) and parallel GPU implementations(runs at NVIDIA K20 GPU with 2493 cores).The speedup factor for four simulation cases is shown in Table 2.The larger the basis number,the larger computation cost needs. All the simulations are carried out with PGI fortran compiler, the laser is 3.8 fs (which contains about 4000 time steps)and the simulation box isRmax=70. A speed up of 147 is achieved if 4300 basis sets are used. It indicates that as the simulation system size increases, this improvement becomes more and more pronounced.

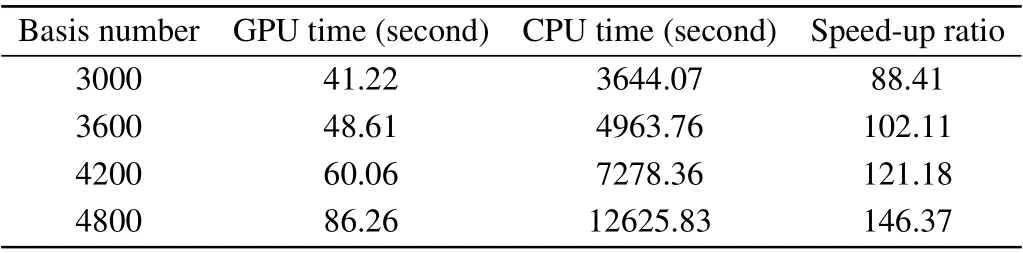
Table 2. The efficiency of our GPU program.

6. Conclusion

In this work, we have presented a program which solves the full-dimension-TDSE of helium using OpenACC+GPU simulation acceleration environment. We introduce how to convert the full-dimension-TDSE into coupled partial differential equations.These partial differential equations are solved by the Adams method. Our program has two advantages:Firstly, the codes are easily parallelled by adding few detectives and have a speed up of 147 on GPU, HeTDSE does not have to use a super computer or a computer cluster, even a desktop computer with an openACC-enable GPU can run HeTDSE efficiently. Secondly,we can transplant our program to other accelerators without rewriting the codes. By comparing with literature of the excited state dynamics and ionization yield of helium,the accuracy of our program has been verified.Our codes can be used to investigate the non-perturbative electronic dynamics of helium subjected to a strong laser pulse. In addition,for the programming for accelerators such as CUDA is difficult, we hope HeTDSE to be an example to help more researchers to handle the GPU calculation more easily using OpenACC.