CLASSIFICATION OF SOLUTIONS TO HIGHER FRACTIONAL ORDER SYSTEMS?
Faculty of Economic Mathematics,University of Economics and Law,Ho Chi Minh City,Vietnam Vietnam National University,Ho Chi Minh City,Vietnam E-mail:phuongl@uel.edu.vn
Abstract Let 0<α,β
Key words Higher fractional order system;integral system;general nonlinearity;method of moving spheres;classification of solutions
1 Introduction
Letn
≥2 be an integer,α,β
be real numbers satisfying 0<α,β<n
,andf,g
∈C
([0,
∞)×[0,
∞))be two nonnegative functions.We study the semilinear elliptic system
and the related integral system
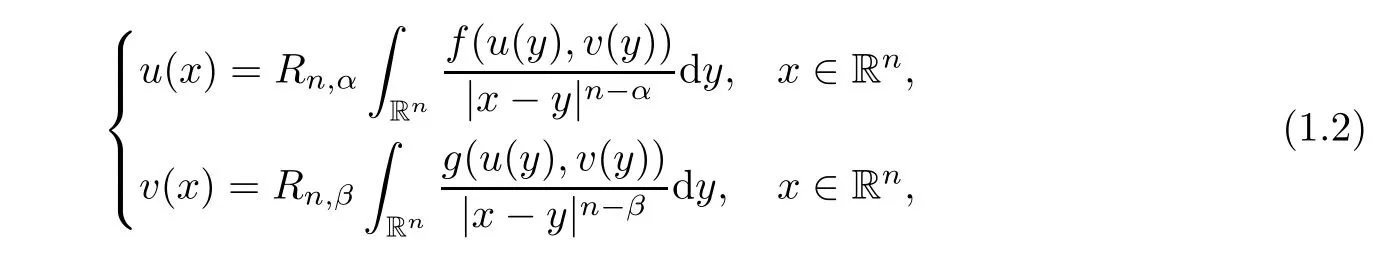

u,v
)a nonnegative solution of(1.1)ifu,v
≥0,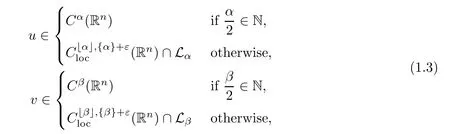
u,v
)veri fies(1.1)point wise,whereε>
0 is arbitrarily small.Moreover,(u,v
)is called trivial if(u,v
)≡(0,
0).In their pioneering article[2],Chen,Li and Ou introduced the method of moving planes in integral forms and used it to establish the radial symmetry of any nonnegative solution to the integral equation
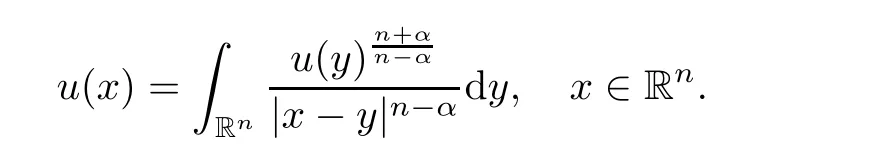
Hence they solved an open problem posed by Lieb[3]regarding the best constant in a Hardy-Little wood-Sobolev inequality.Later,Chen and Li[4]extended this result to the integral system
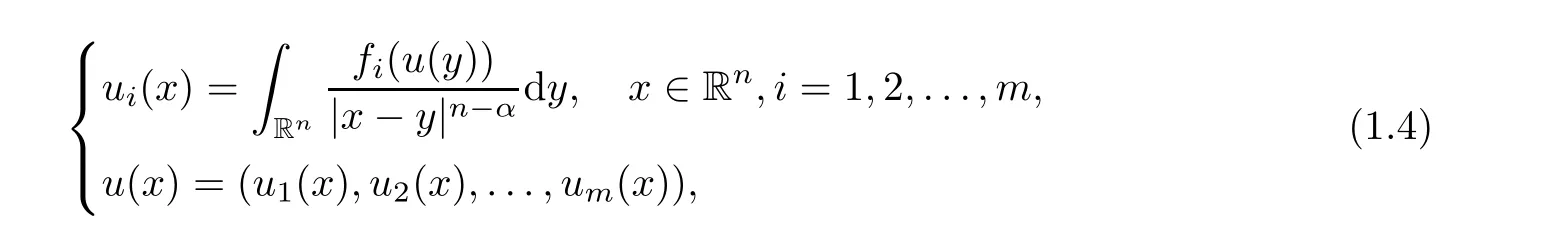
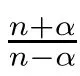

f
andg
.Our monotonicity conditions onf
andg
are similar to those in[9].However,we do not assumef,g
∈C
orα
=β
.To overcome the difficulty caused by weaker assumptions,we introduce some new ideas.We also use the method of moving spheres instead of moving planes to obtain the explicit forms of the solutions more easily.Our result,therefore,improves and uni fies both results in[7]and[9].To state our first result,we denote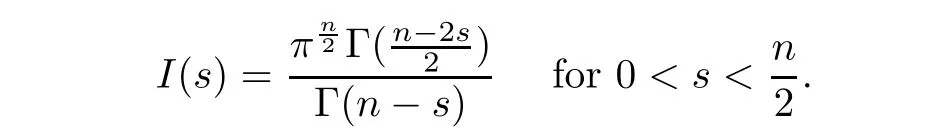
Theorem 1.1
Let 0<α,β<n
andf,g
∈C
([0,
∞)×[0,
∞))be two nonnegative functions such that
c
,c
,μ>
0 andx
∈R.Moreover,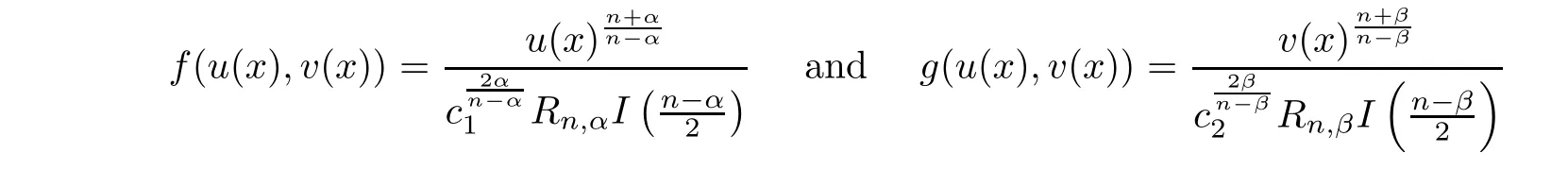
x
∈R.Remark 1.2
The assumption thatf
(s,t
)is increasing int
andg
(s,t
)is increasing ins
is to ensure that the system is non-degenerate.This non-degeneracy assumption was proposed in[4]and was also used in[9].Without this assumption,system(1.2)may contain two unrelated equations such as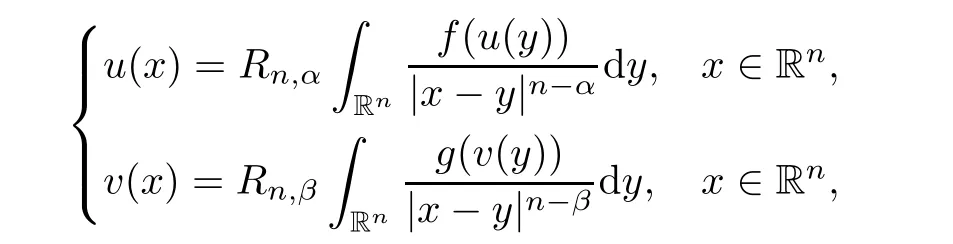
u,v
may not have the same symmetric center in such a case.Remark 1.3
For the simplicity of the presentation,we only consider systems of two equations in this paper.However,our method can be extended to integral systems with more equations as in[9].Next,we discuss the classification of nonnegative classical solutions of elliptic system(1.1).We first mention the case of a single equation.Several authors have contributed to a classification result stated that every nonnegative classical solution to the critical semilinear elliptic equation
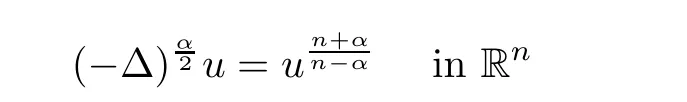
must assume the form
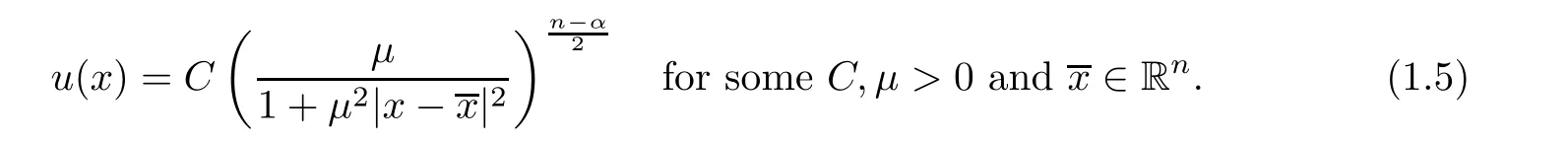
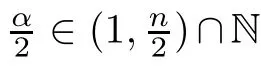

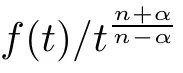
α
=β
=2 andf,g
satisfy some monotonicity conditions.Later,a fractional counterpart result was derived by Li and Ma[21]using the direct method of moving planes.More precisely,Li and Ma assumed that(u,v
)is a nonnegative solution of(1.1)and?0<α,β<
2,f
(s,r
)≡f
(r
),g
(r,t
)≡g
(r
),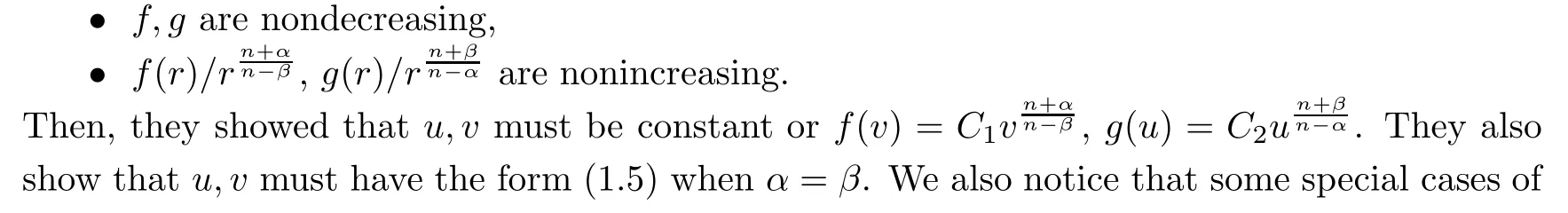

Theorem 1.4
Assume thatf
andg
satisfy all assumptions of Theorem 1.1 and one of the following conditions holds: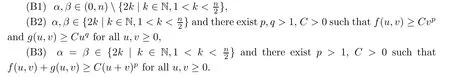
u,v
)is a nonnegative nontrivial classical solution of system(1.1).Then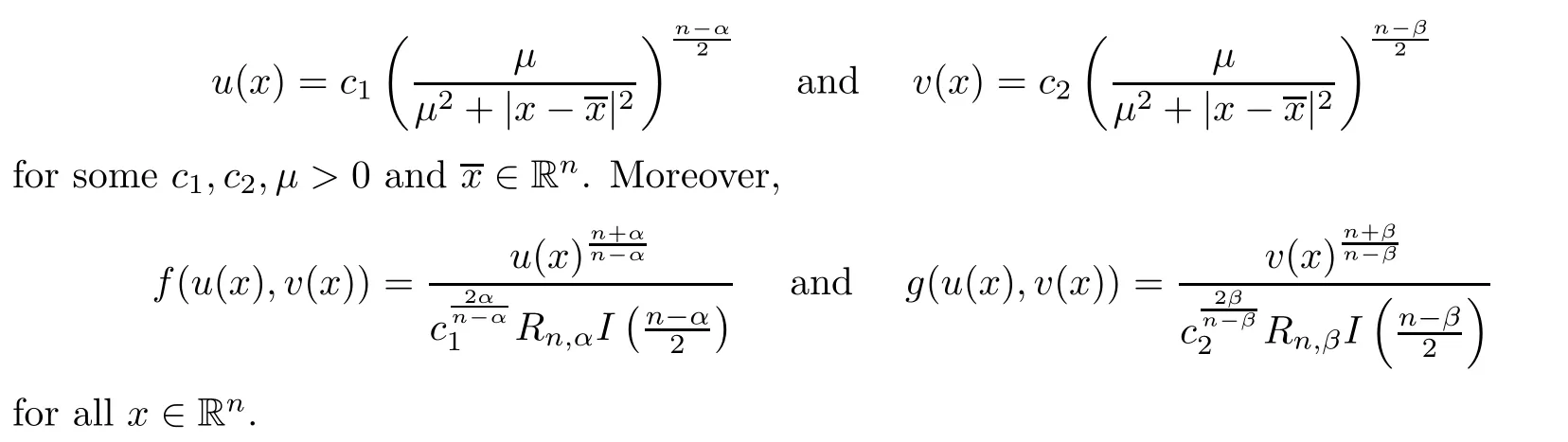
f
andg
.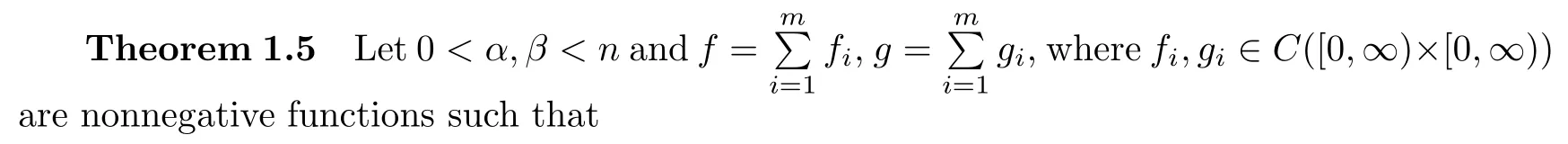
f
(s,t
)is nondecreasing ins
and increasing int
,(ii)g
(s,t
)is increasing ins
and nondecreasing int
,(iii)For everyi
=1,
2,...,m
,there existp
,p
≥0,(n
?α
)p
+(n
?β
)p
=n
+α
such thatf
(s,t
)/
(s
t
)is nonincreasing in each variable,(iv)For everyi
=1,
2,...,m
,there existq
,q
≥0,(n
?α
)q
+(n
?β
)q
=n
+β
such thatg
(s,t
)/
(s
t
)is nonincreasing in each variable.Assume that(u,v
)∈C
(R)×C
(R)is a nonnegative nontrivial solution of system(1.2).Then
c
,c
,μ>
0 andx
∈R.Moreover,for all(s,t
)∈[0,
maxu
]×[0,
maxv
],whereC
,C
>
0 satisfy
u,v
)of system(1.1)if we further assume that(B1),(B2),(B3)are satis fied.Remark 1.6
Theorem 1.5 extends[7,Theorem 4]to the caseα
/=β
.Some special cases of the last statement of Theorem 1.5 were previously proved in[8](whenα
=β
=2)and[21](when 0<α,β<
2).In particular,Theorem 1.5 can be applied to the system
We can state the following corollary of Theorem 1.5,which improves[5,22,29].

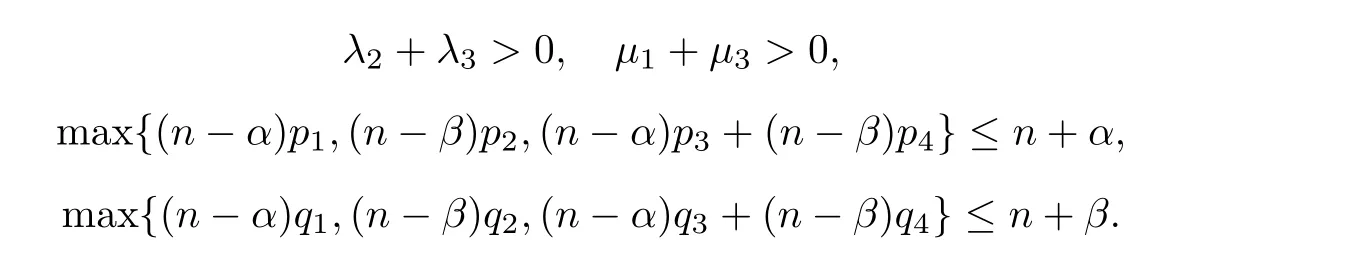
u,v
)is a nonnegative nontrivial classical solution of system(1.7).Then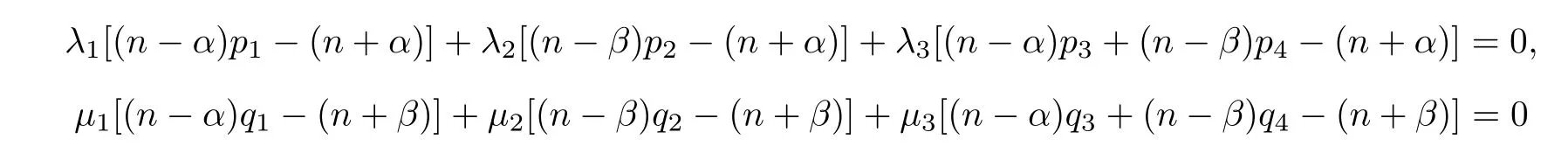
u,v
)assumes the form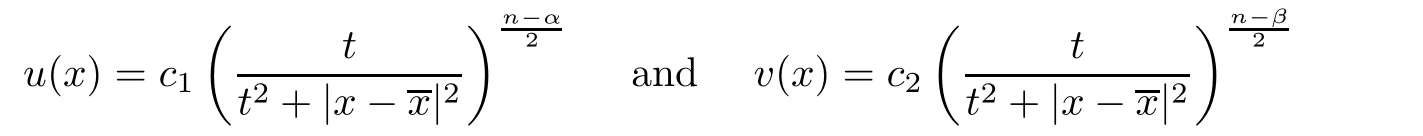
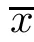
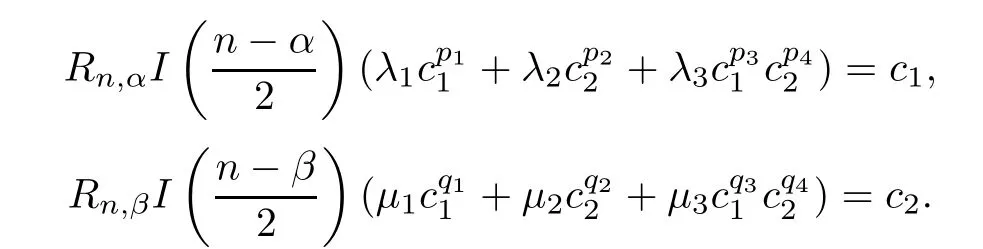
f
andg
can be explicitly derived.Throughout this paper,we denote byB
(x
)the ball of radiusR>
0 with centerx
∈R.For brevity,we will writeB
=B
(0).We also useC
to denote various positive constants whose values may change from place to place.2 Classification of Nonnegative Solutions to the Integral System
To prove Theorem 1.1,we employ the method of moving spheres in integral forms.It is different from the moving plane method used by other authors we mentioned in the introduction section.The method of moving spheres was introduced by Li and Zhu[30].Lately,Li and Zhang[31]and Li[32]improved Li and Zhu’s two calculus key lemmas.An advantage of this method is that it can immediately yield the explicit form of solutions to elliptic equations satisfying certain conformal invariance and the nonexistence to elliptic equations with subcritical exponent.Hence it is not necessary to prove the symmetry of solutions beforehand as in the method of moving planes.
Since we do not assume thatf,g
are differentiable,we cannot use the mean value theorem to obtain integral estimates as in[4,9].Our new idea is to exploit the following inequality in our later estimation:Lemma 2.1
Assume thatf
satis fies(A1).Then for allt
>t
>
0 ands>
0,we have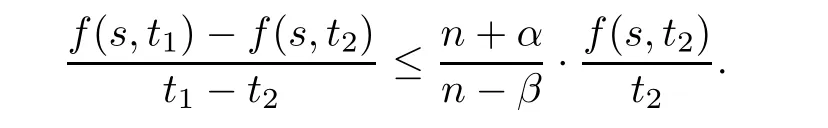
t>
0 ands
>s
>
0,we have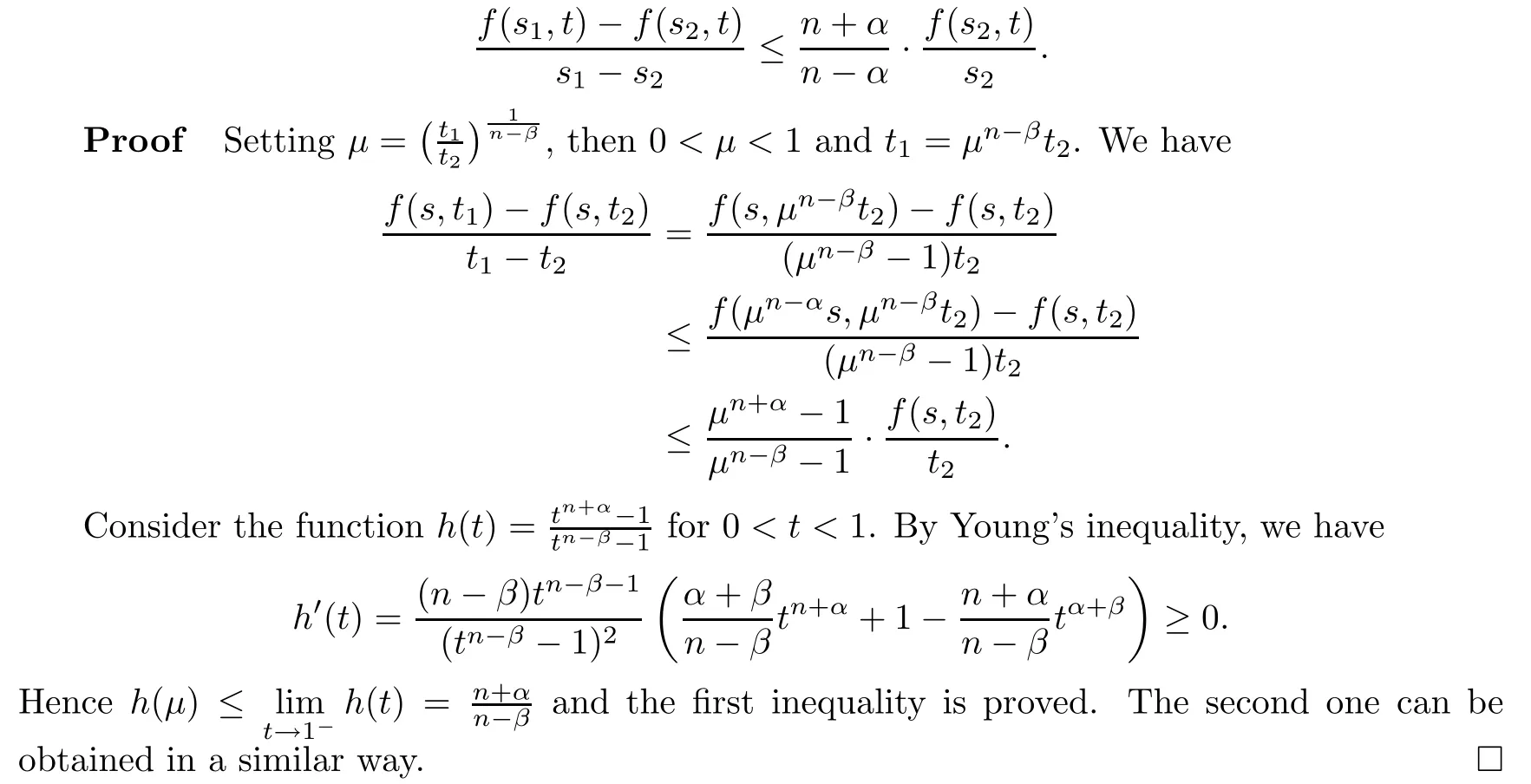
u,v
)∈C
(R)×C
(R)be a nonnegative nontrivial solution of system(1.2).Then,it follows thatu
andv
are positive.For anyx
∈Randλ>
0,we denote by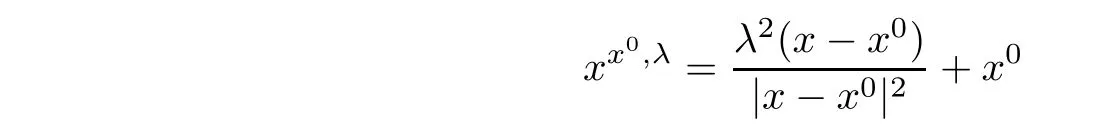
x
∈R{x
}about the sphere?B
(x
).Then,we de fine the Kelvin transform ofu
andv
with respect to?B
(x
)by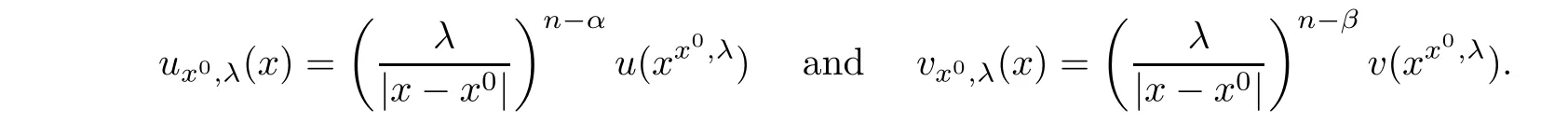
We also de fine

We will use the method of moving spheres in integral forms to prove the following proposition:
Proposition 2.2
For anyx
∈R,the set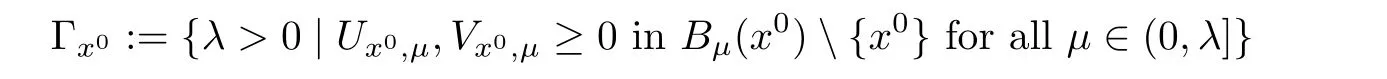
λ
:=supΓ<
∞,thenU
=V
=0 inB
(x
){x
}.Since system(1.2)is invariant by translations,it suffices to prove Proposition 2.2 forx
=0.For the sake of simplicity,we will drop the subscriptx
in the notations whenx
=0.That is,we will write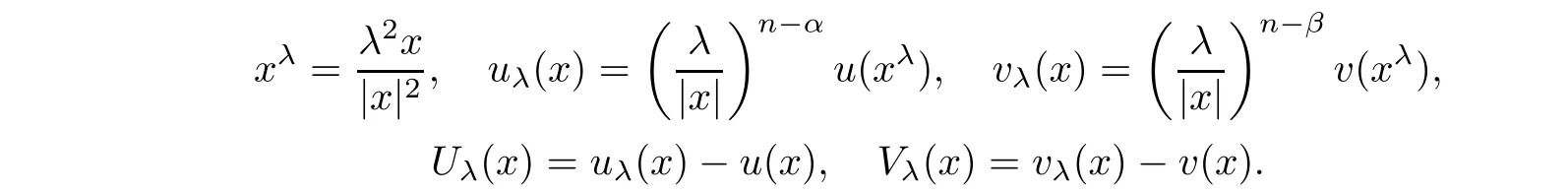
u
,v
)satis fies,for allx
∈R{0},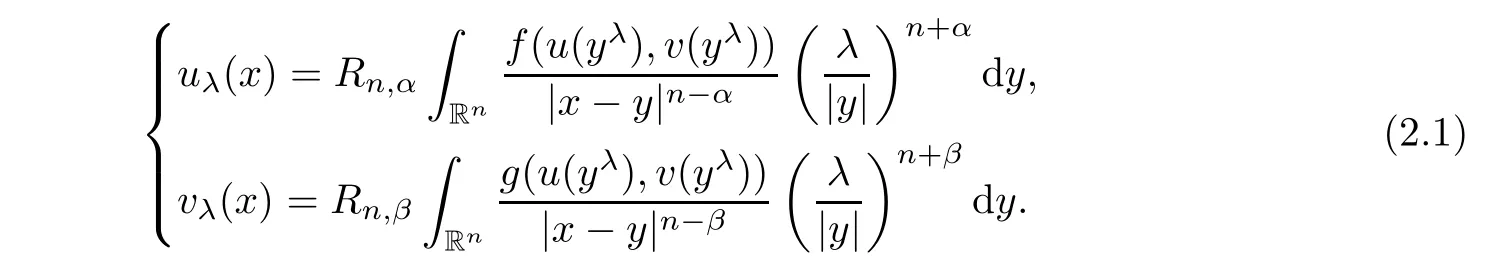
Indeed,using the first equation in(1.2),we have
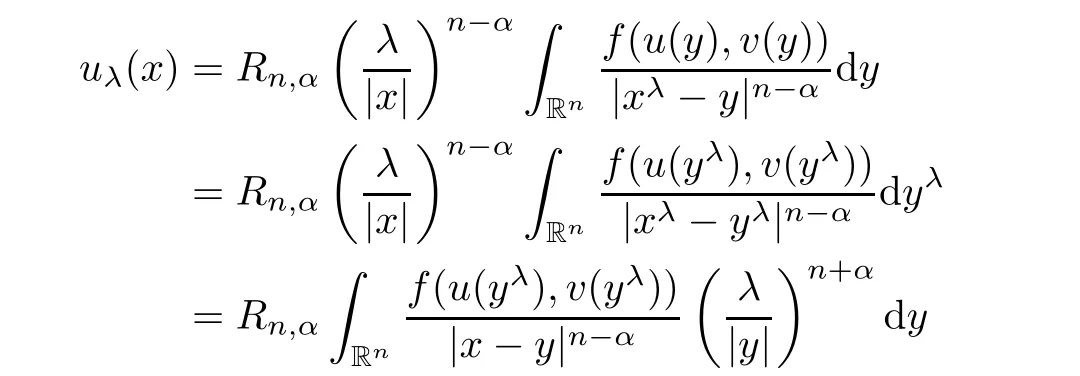
x
∈R{0},where we have used the following identities in the last line: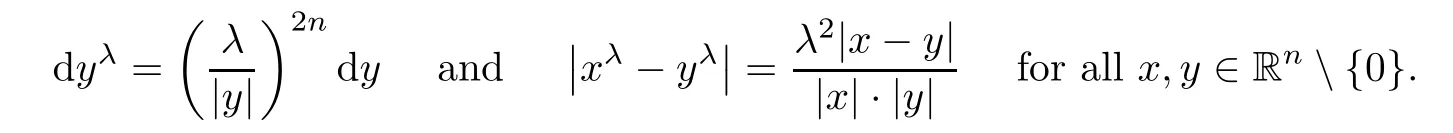
The second equation in(2.1)can be obtained in the same way.
Next,for eachλ>
0,we denote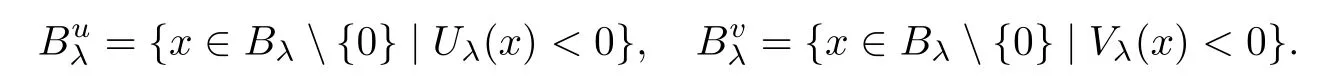
We prove key integral estimates which will be used in the proof of Proposition 2.2.
Lemma 2.3
If 0<λ<λ
,then there existsC>
0,which depends onλ
but is independent ofλ
,such that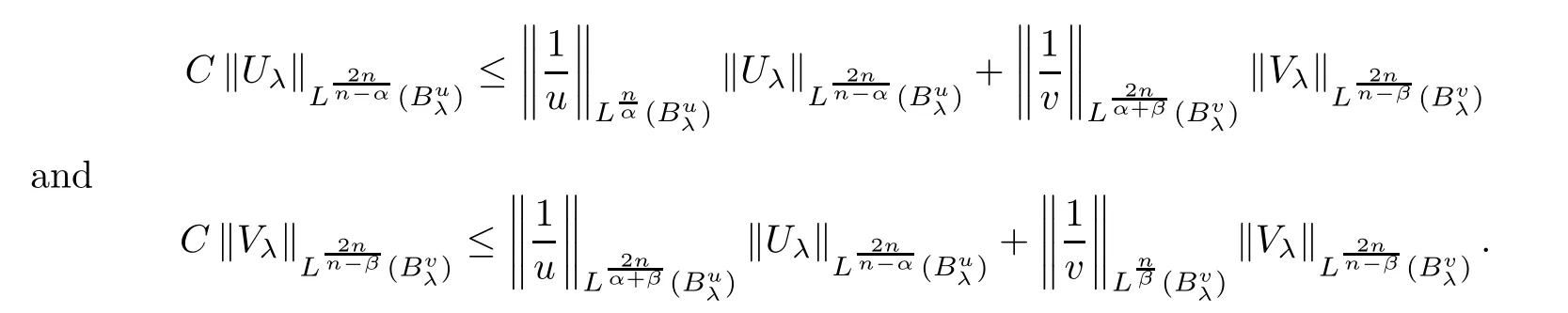
Proof
Let anyx
∈B
{0}.From the first equation in(1.2),we have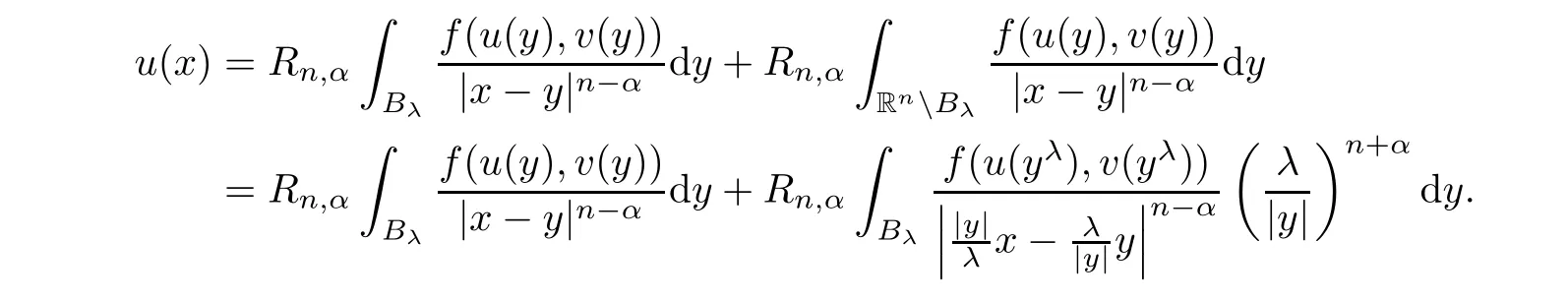
Similarly,from the first equation in(2.1),we obtain
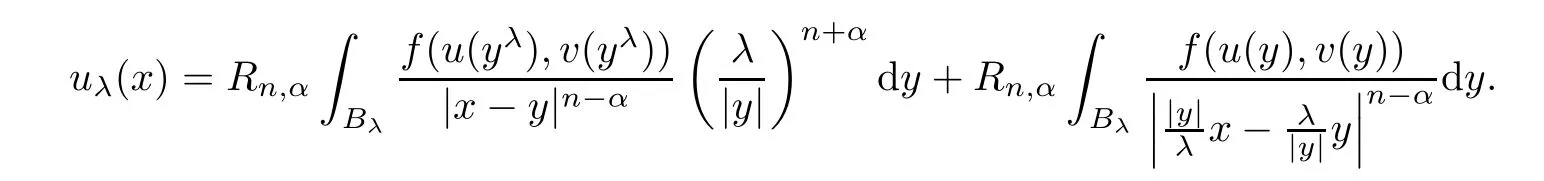
Combining the above two formula,we derive

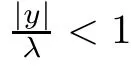
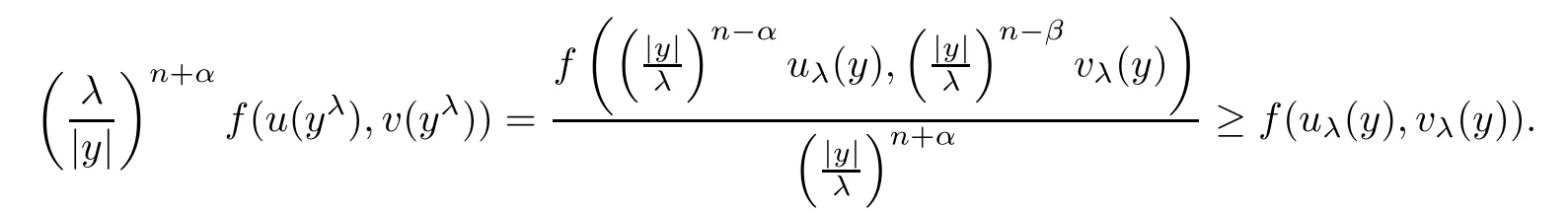
Combining this with(2.2)and(2.3),we obtain
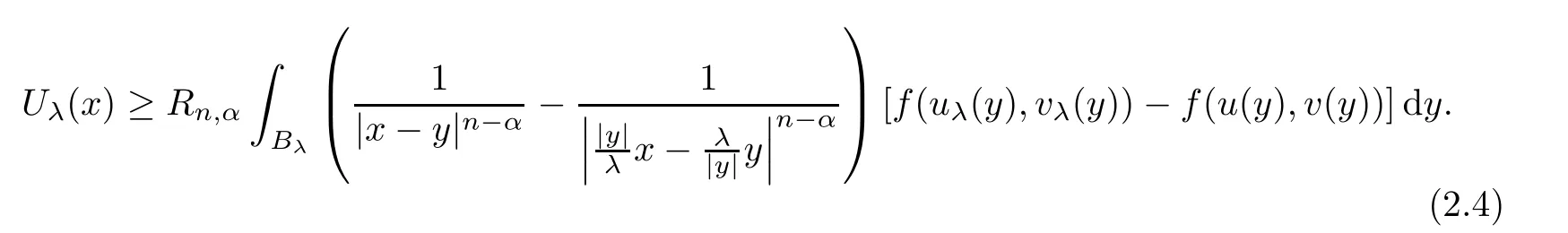
Using Lemma 2.1,we have
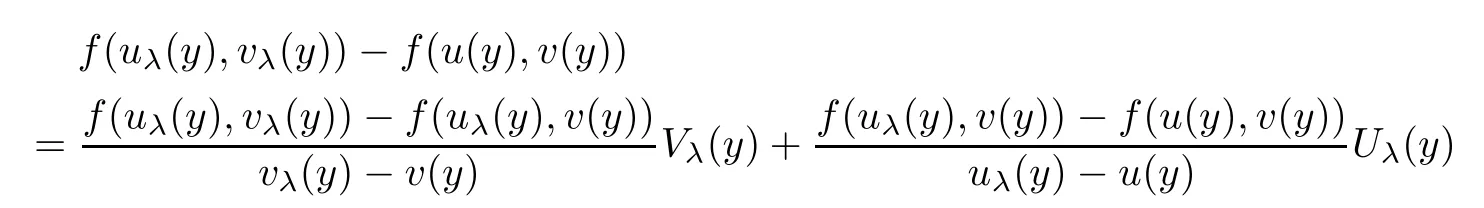
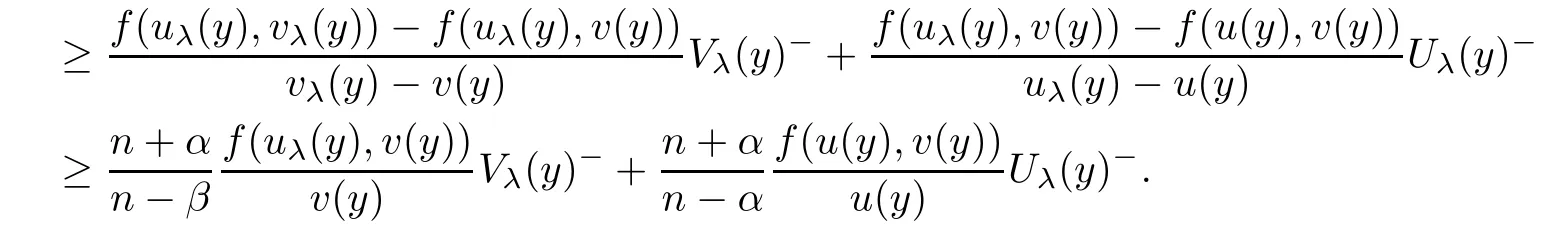
u
(y
)<u
(y
),then from the above inequality,we have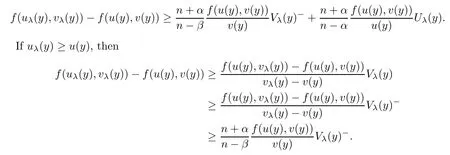
y
∈B
{0},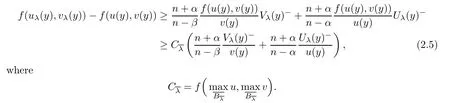
From(2.4),(2.3)and(2.5),we deduce

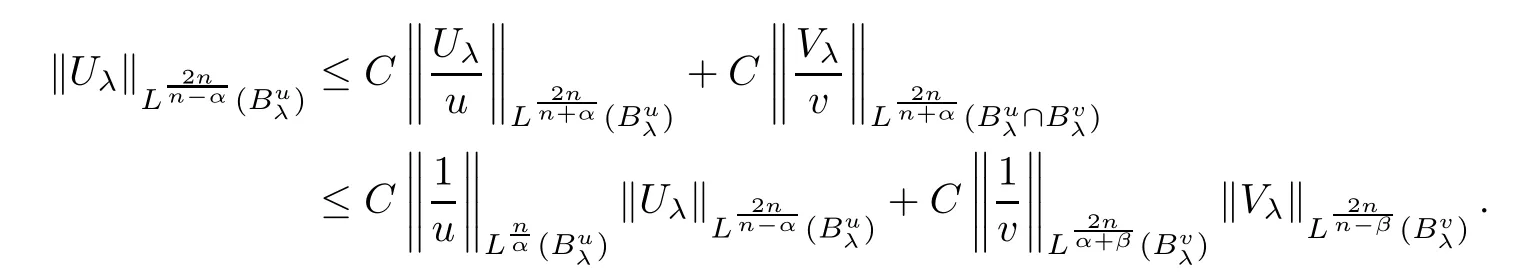
The second inequality can be derived in a similar way.
Proof of Proposition 2.2
As mentioned before,we only need to prove the proposition forx
=0.Step 1
(Start dilating the sphere?B
from nearλ
=0)In this step,we prove that Γ/=?,that is,forλ>
0 sufficiently small,
u
andv
are continuous and positive,there existsε
∈(0,
1)small enough,such that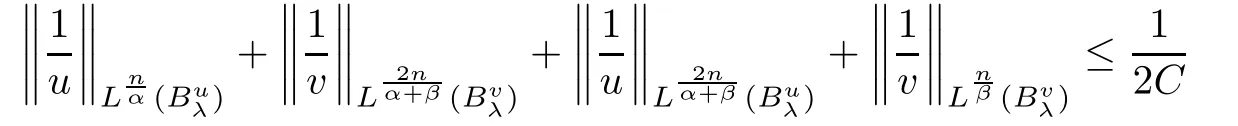
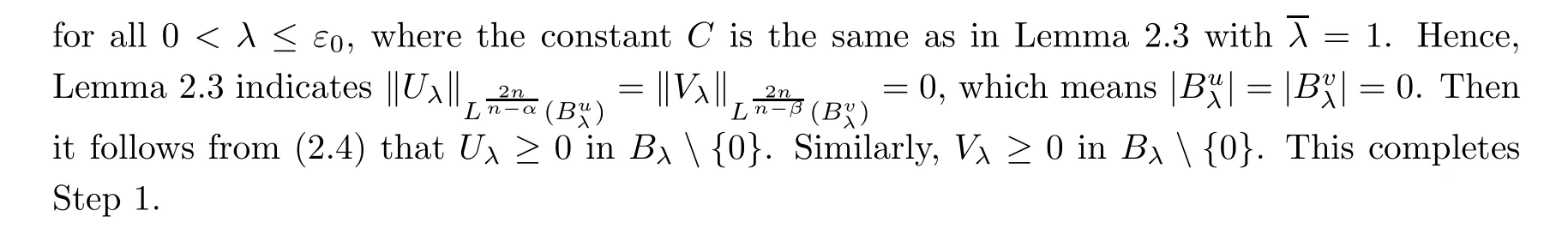
Step 2
(Dilate the sphere?B
outward to the limiting position)Step 1 provides us a starting point to dilate the sphere?B
from nearλ
=0.Now we dilate the sphere?B
outward as long as(2.6)holds.Let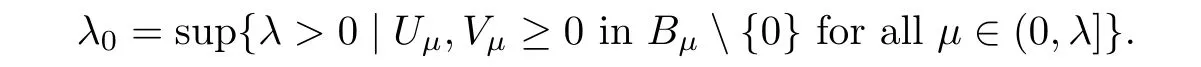
In this step,we show that

λ
<
∞andV
/≡0 inB
{0}.SinceU
,V
are continuous with respect toλ
,we already haveU
,V
≥0 inB
{0}.From(2.4),we have
U
>
0 inB
{0}.Then using a similar reasoning,we haveV
>
0 inB
{0}.Next,we claim that there existsC>
0 andη>
0 such that
Indeed,from(2.8)and Fatou’s lemma,we have
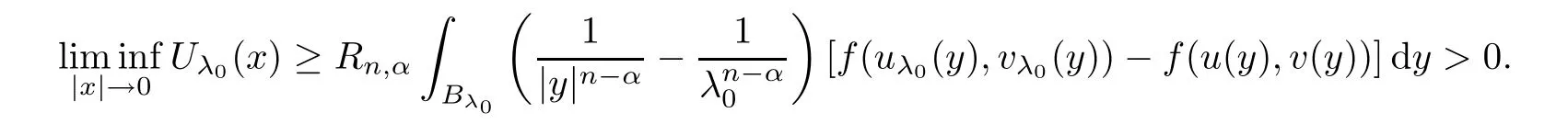
x
∈B
{0},whereη
is sufficiently small,we haveU
(x
)≥C
.Similarly,forx
∈B
{0},whereη
is chosen smaller if necessary,we also haveV
(x
)≥C
.This proves(2.9).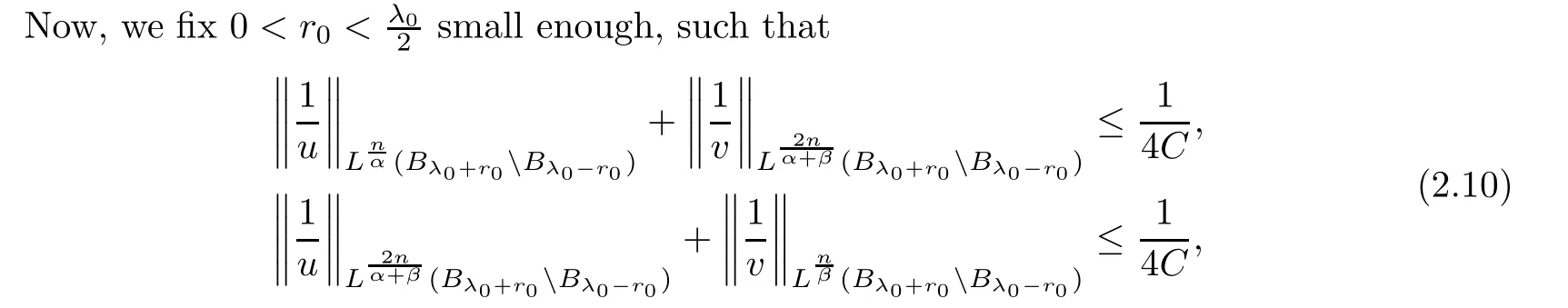

U
andV
,we can find a constantC>
0 such that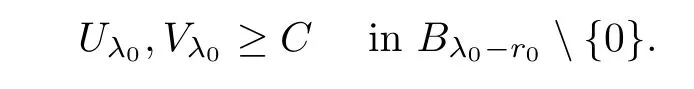
u
andv
are uniformly continuous on an arbitrary compact set,there existsρ
∈(0,r
)such that,for anyλ
∈(λ
,λ
+ρ
),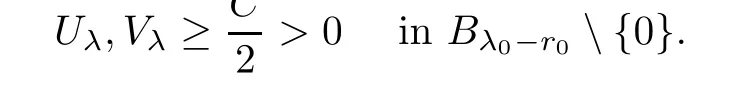
λ
∈(λ
,λ
+ρ
),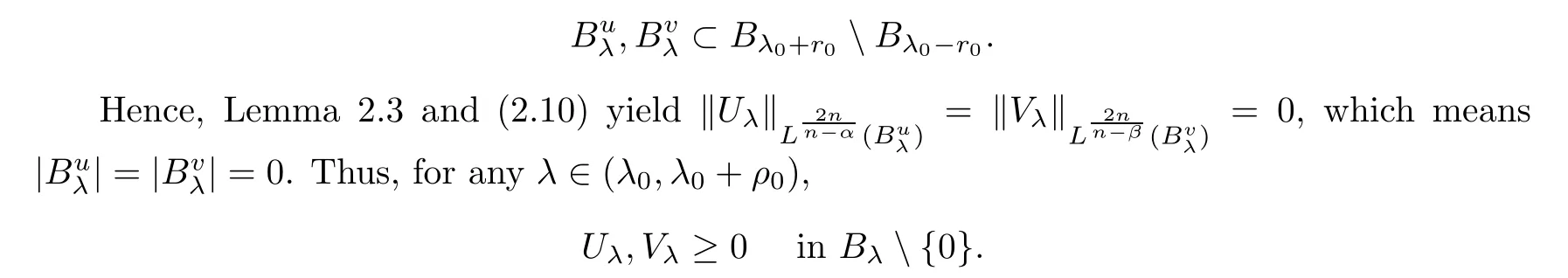
λ
and(2.7)is proved.This completes the proof of Proposition 2.2.
To obtain explicit forms of all nonnegative solutions of(1.2),we need the following calculus lemma:
Lemma 2.4
(See Appendix B in[32])Letn
≥1,ν
∈R andw
∈C
(R).For everyx
∈Randλ>
0,we de fine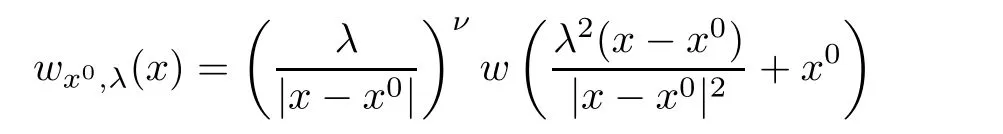
x
∈R{x
}.Then,we have the following:(i)If for everyx
∈R,there existsλ
<
∞such that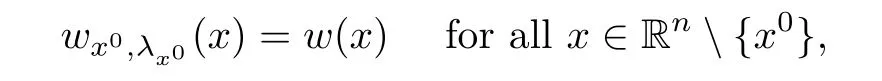
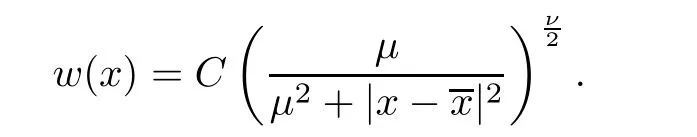
x
∈R,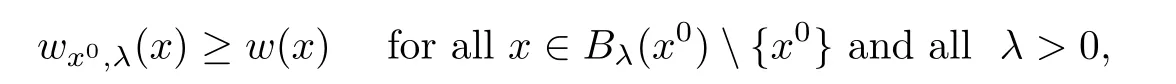
w
≡C
for some constantC
∈R.Remark 2.5
If case(i)of Lemma 2.4 happens,then a direct computation yields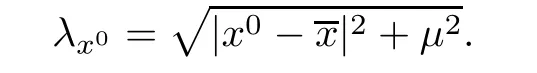
We are ready to prove the main result in this section,namely,Theorem 1.1.
Proof of Theorem 1.1
There are three cases.Case 1
There existx
,y
∈Rsuch thatλ
=∞andλ
<
∞.Sinceλ
=∞,we have,for anyλ>
0,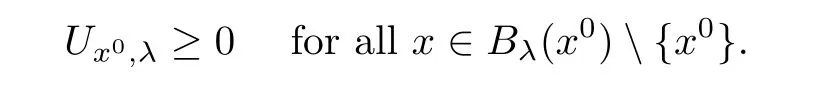
λ>
0,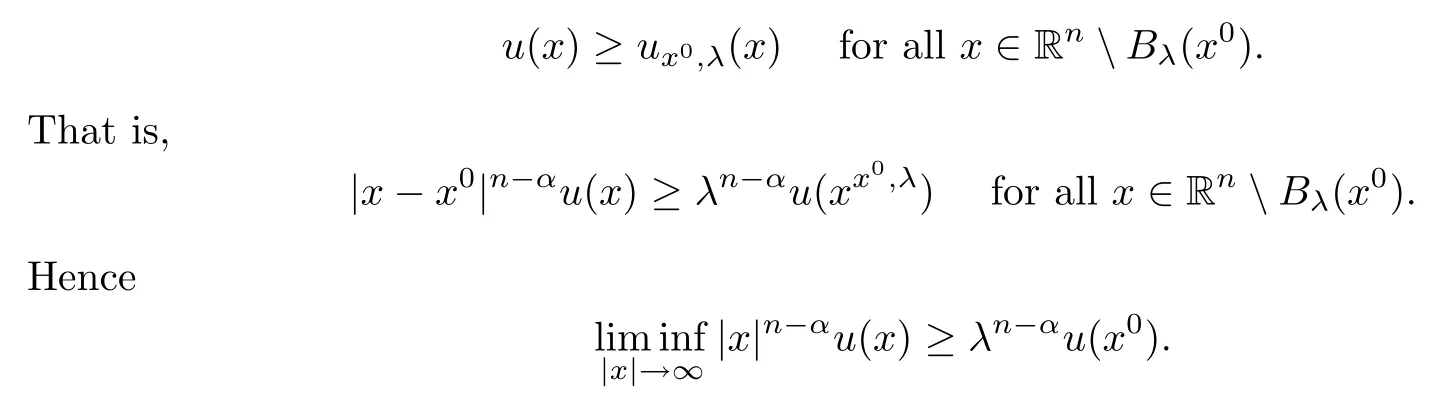
λ>
0,we must have
λ
<
∞,we may use Proposition 2.2 to get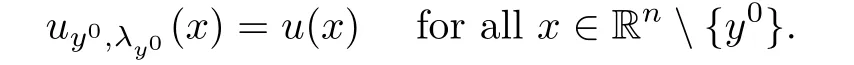
This indicates that
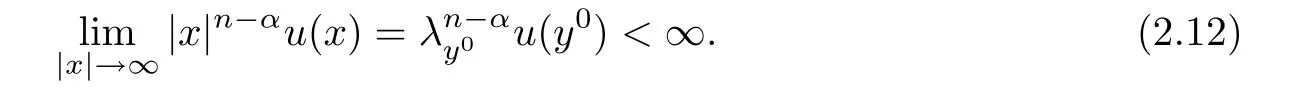
The contradiction between(2.11)and(2.12)indicates that Case 1 cannot happen.
Case 2
For everyx
∈R,the critical scaleλ
=∞.By Lemma 2.4(ii)and the positivity ofu
andv
,we have(u,v
)≡(C
,C
)for some constantsC
,C
>
0.This is absurd since positive constant functions do not satisfy(1.2).Case 3
For everyx
∈R,the critical scaleλ
<
∞.From Proposition 2.2,we have

u,v
)must assume the form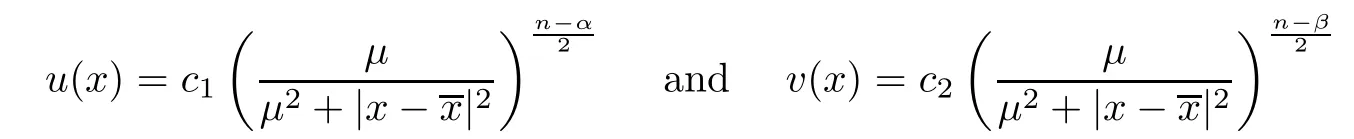
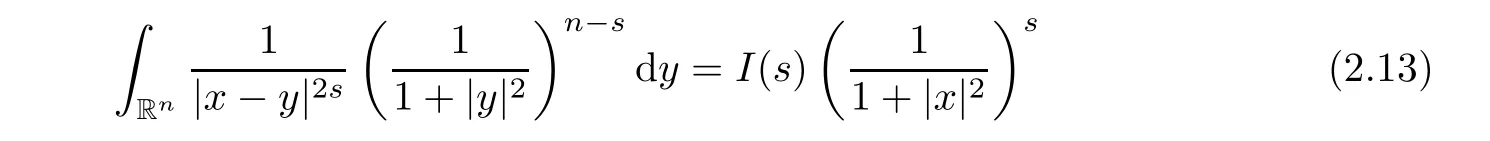
(see(37)in[33]).Using(2.13),we obtain
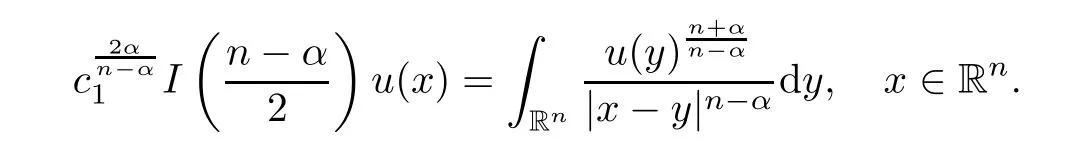
Hence,we deduce

Similarly,
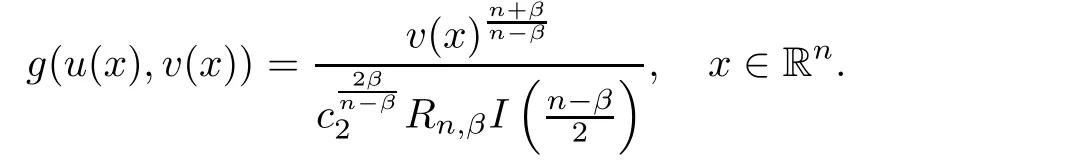
This completes the proof of Theorem 1.1.
3 Classification of Nonnegative Solutions to the System of PDEs
We exploit the ideas in[2]to establish the equivalence of systems(1.1)and(1.2).Then,we prove Theorem 1.4 in this section.
Proposition 3.1
Letf,g
∈C
([0,
∞)×[0,
∞))be two nonnegative functions and assume that either assumption(B1),(B2)or(B3)of Theorem 1.4 is satis fied.Suppose that(u,v
)is a nonnegative classical solution of(1.1),then(u,v
)is also a nonnegative solution of(1.2),and vice versa.Proof
Suppose that(u,v
)is a nonnegative classical solution of(1.1).Then,(u,v
)satis fies the super polyharmonic property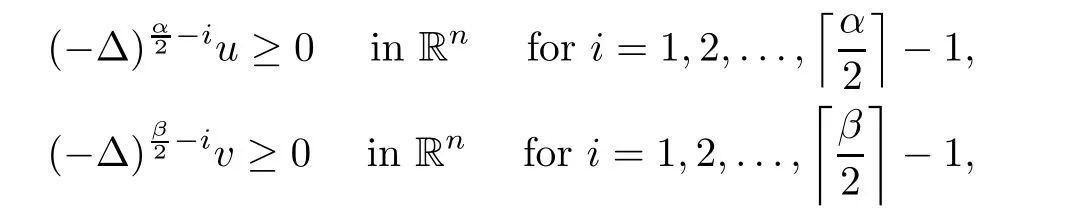
t
?denotes the smallest integer which is not smaller thant
.Indeed,such the property was proved in[15,Theorem 1.1]if(B1)holds,in[26,Theorem 2]if (B2)holds and in[26,Theorem1]if(B3)holds.
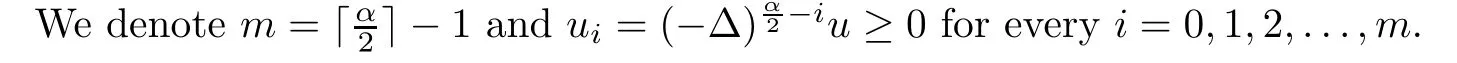
n
=2,thenm
=0 and we can go directly to Case 2 below.Hence,in deriving form ulae(3.1)below,we may assumen
≥3.We observe thatu
is a nonnegative solution of the equation??u
=u
=f
(u,v
)in R.For anyR>
0,let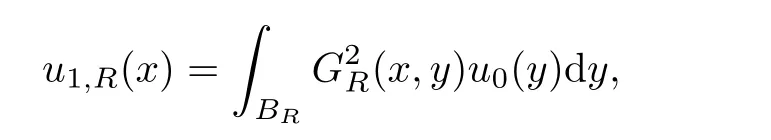
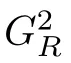

From the maximum principle,we have
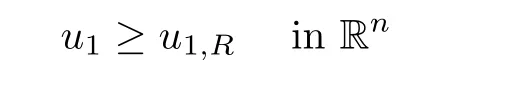
R>
0.For each fixedx
∈R,lettingR
→∞,we obtain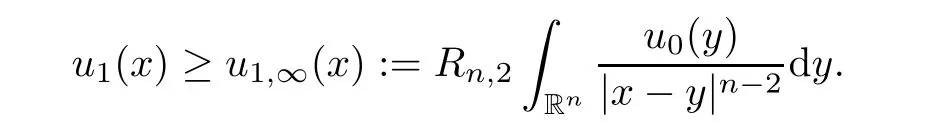
u
satis fies??u
=u
in R.Hence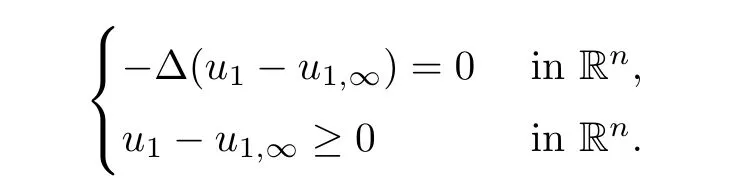
u
?u
≡C
≥0.That is,
u
is a nonnegative solution of the equation??u
=u
in Rfori
=1,
2,...,m
,we deduce that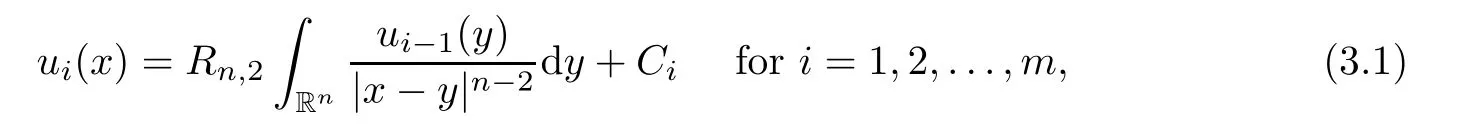
C
≥0.Now we setγ
=α
?2m
,thenγ
∈(0,
2].We consider two cases.Case 1
γ
=2In this case,u
is a nonnegative solution of the equation??u
=u
in R.Hence we can use the above argument to obtain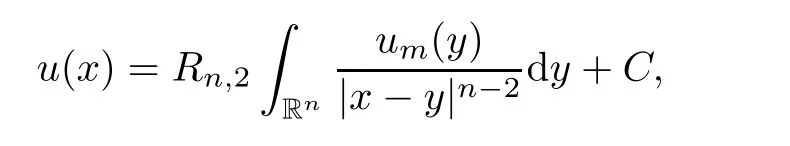
C
≥0.Case 2
γ
∈(0,
2)In this case,u
is a nonnegative solution of the fractional equation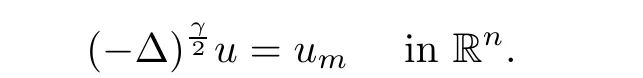
R>
0,let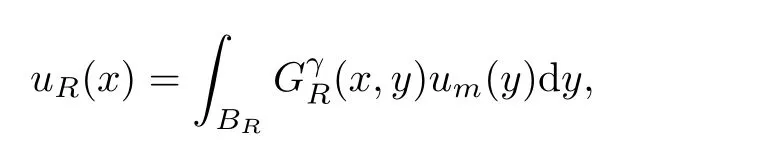
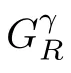

γ
-superharmonic functions(see[1,14]),we deduce that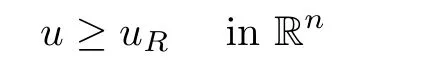
R>
0.For each fixedx
∈R,lettingR
→∞,we have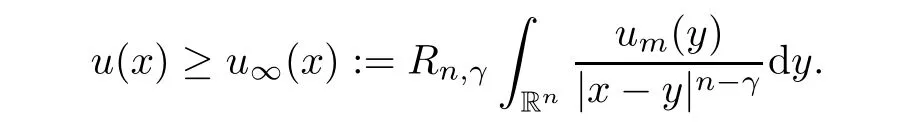
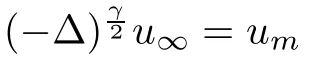
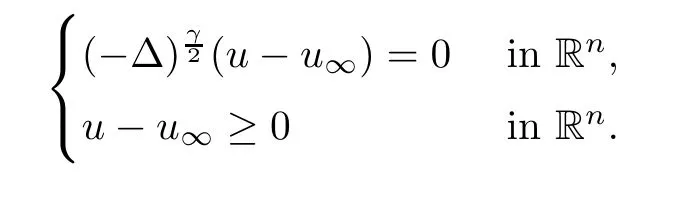
γ
-harmonic functions(see[25]),we can deduce thatu
?u
≡C
≥0.That is,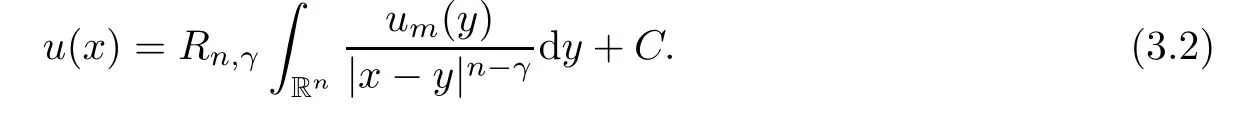
m>
0)and(3.2).Moreover,we must have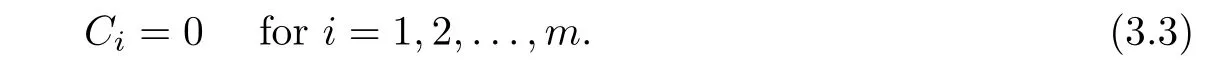
C
>
0 for somei
∈{1,
2,...,m
?1},then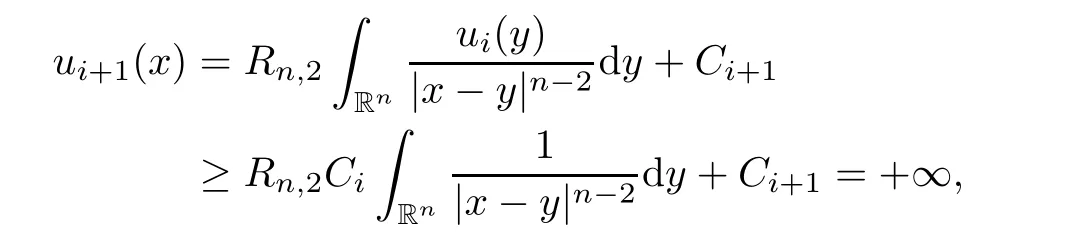
C
>
0,then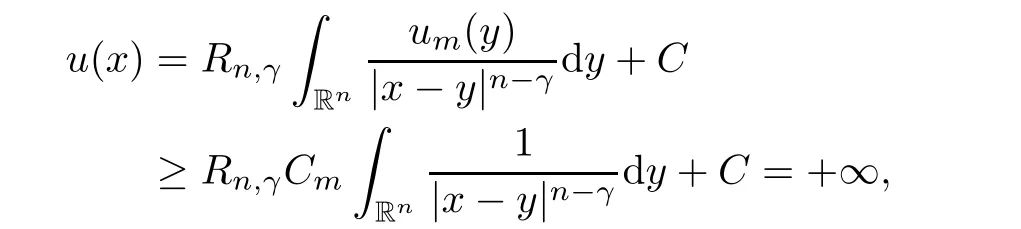
which is also absurd.
From(3.1),(3.2)and(3.3),we deduce
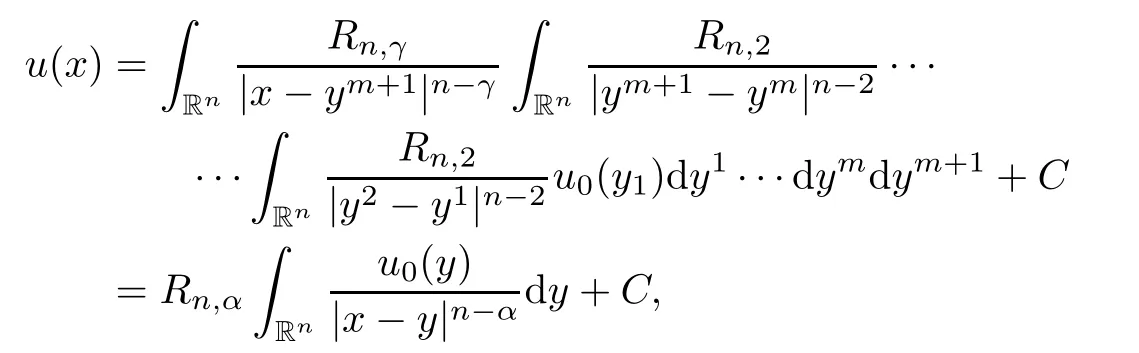
where in the last equality,we have used Fubini’s theorem and the following Selberg formula:
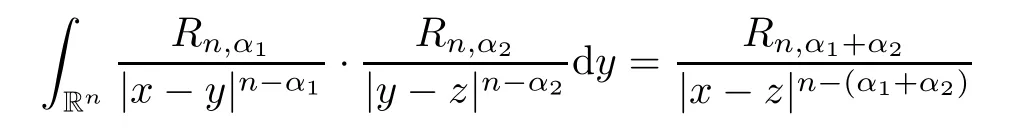
α
,α
∈(0,n
)such thatα
+α
∈(0,n
)(see[36]).We have proved that
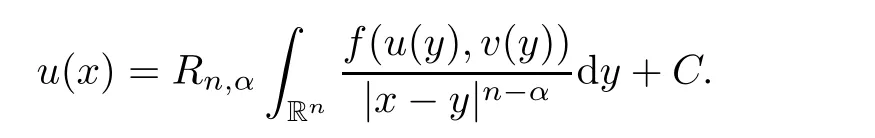
Similarly,
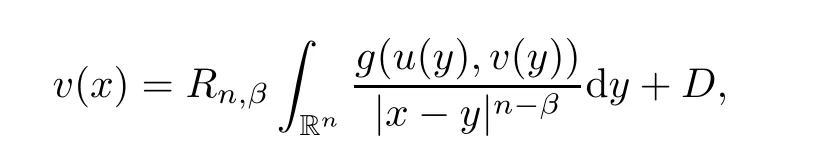
D
≥0.We claim thatC
=D
=0.Otherwise,supposeC>
0,then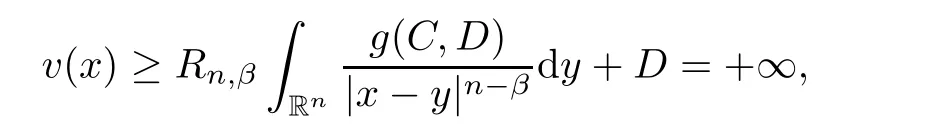
C
=D
=0 and(u,v
)is a nonnegative solution of(1.2).Conversely,assume that(u,v
)satis fies(1.3)and(u,v
)is a nonnegative solution of(1.2).We have
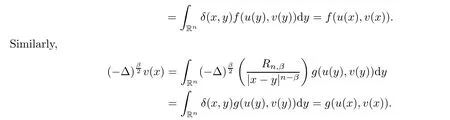
u,v
)is a nonnegative solution of(1.1).Proof of Theorem 1.4
Theorem 1.4 is a direct consequence of Theorem 1.1 and Proposition 3.1.4 A Special Case
In this section,we prove Theorem 1.5.Basically,it is a consequence of Theorem 1.1 and Proposition 3.1.
Proof of Theorem 1.5
Let(u,v
)∈C
(R)×C
(R)be a nonnegative nontrivial solution of system(1.2).Thenu,v>
0.For eachi
=1,
2,...,m
,we de fine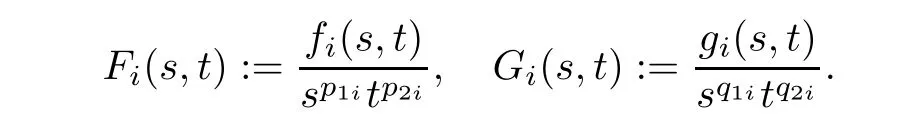
F
,G
are nonincreasing in each variable.Notice that for alls,t
≥0,μ>
0,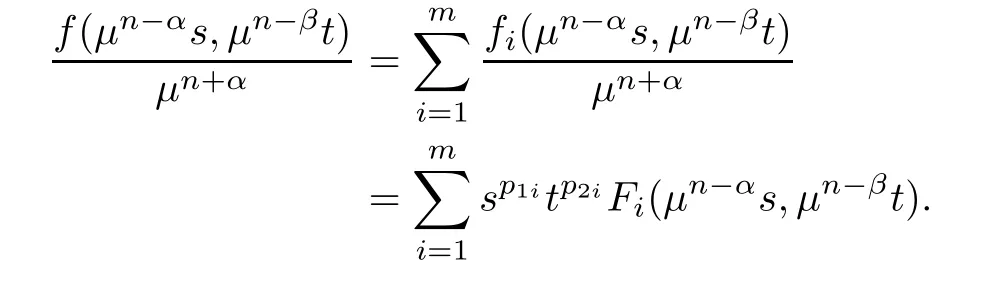
f
satis fies(A1).By a similar reasoning,we see thatg
satis fies(A2).Therefore,by applying Theorem 1.1,we deduce that(u,v
)must have the form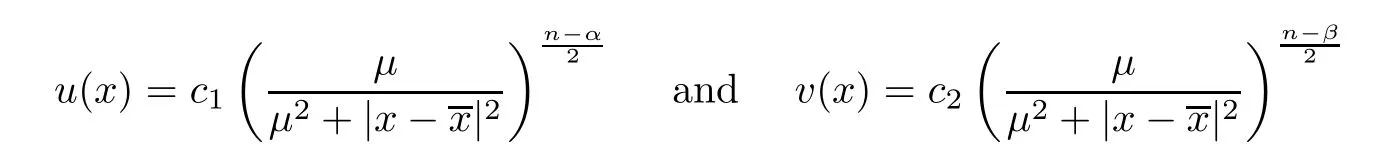
c
,c
,μ>
0 andx
∈R.Moreover,
x
∈R.Hence
x
∈R.Using the assumption that allF
are nonincreasing in each variable and the fact thatu,v
decay at in finity and attain their maximums atx
,we conclude thatF
(s,t
)=C
for all(s,t
)∈[0,
maxu
]×[0,
maxv
],i
=1,
2,...,m
,where positive constantsC
satisfy
which means

G
(s,t
)=C
for all(s,t
)∈[0,
maxu
]×[0,
maxv
],whereC
>
0 and
f
andg
have the desired forms.The first part of the theorem is proved.Now we assume that(u,v
)is a nonnegative nontrivial classical solution of system(1.1)and(B1),(B2),(B3)are satis fied.In this situation,we may use Proposition 3.1 to deduce that(u,v
)is a nonnegative solution of(1.2).Then,we can derive the same conclusion as above. Acta Mathematica Scientia(English Series)2021年4期
Acta Mathematica Scientia(English Series)2021年4期
- Acta Mathematica Scientia(English Series)的其它文章
- REGULARITY OF WEAK SOLUTIONS TO A CLASS OF NONLINEAR PROBLEM?
- EXISTENCE TO FRACTIONAL CRITICAL EQUATION WITH HARDY-LITTLEWOOD-SOBOLEV NONLINEARITIES?
- A DIFFUSIVE SVEIR EPIDEMIC MODEL WITH TIME DELAY AND GENERAL INCIDENCE?
- ON A COUPLED INTEGRO-DIFFERENTIAL SYSTEM INVOLVING MIXED FRACTIONAL DERIVATIVES AND INTEGRALS OF DIFFERENT ORDERS?
- ENERGY CONSERVATION FOR SOLUTIONS OF INCOMPRESSIBLE VISCOELASTIC FLUIDS?
- JULIA LIMITING DIRECTIONS OF ENTIRE SOLUTIONS OF COMPLEX DIFFERENTIAL EQUATIONS?
