Wei Zhao(趙偉) Jia-Lin Cheng(成家林) Gong Li(李工) and Xin Wang(王辛)

1School of Materials Science and Engineering,Nanjing Institute of Technology,Nanjing 211167,China

2State Key Laboratory of Metastable Materials Science and Technology,Yanshan University,Qinhuangdao 066004,China

3Jiangsu Key Laboratory of Advanced Structural Materials and Application Technology,Nanjing 211167,China

4School of Materials Science and Engineering,Harbin University of Science and Technology,Harbin 150080,China

Keywords: atomic bond proportion,correction factor,amorphous materials,microstructure

1. Introduction

Conventional alloys are usually crystalline materials and their inner atoms are well ordered. In some special cases,such as the liquid alloy in rapid cooling solidification, the atoms in liquid alloy lacks sufficient time to achieve a completely ordered arrangement and crystallization, and may form a relatively stable amorphous alloy with a disordered solid state structure within a certain duration and temperature range.[1-4]The amorphous alloys differ from crystalline alloys by the former’s lack of grain and grain boundary. Therefore, amorphous alloys possess many unique properties,such as excellent magnetism, corrosion resistance, and wear resistance; high strength, hardness, and toughness; and high resistivity and electromechanical coupling properties.[4-6]Given their excellent performance and simple preparation, amorphous alloys have been the focus of the research and development of materials science and technology since the 1980s. The properties of amorphous alloys are generally determined by their composition and structure. Owing to the lack of a mathematical physical model and reliable theory method, the structures of new amorphous materials remain difficult to be understood.Therefore, studying the microstructure of amorphous alloys and establishing a mathematical physical model are essential to guide the design and development of amorphous alloys on the basis of their structural characteristics. In the long process of amorphous alloy research, a series of structure models have been proposed, such as the microcrystalline model,model of dense random packing of hard spheres,efficient cluster packing model,[7]icosahedral packing model,[8]and model of self-similar packing of atomic clusters.[9]However, these schemes have failed to establish a direct relationship between the structure and properties of the amorphous alloys. In our previous study,[1]a new structural parameter, namely, atomic bond proportion, was proposed and the corresponding calculation method was given. This new structure theory holds that the atomic bond proportion in amorphous alloys entirely composed of metallic elements(without non-metallic elements)is only related to the mole percentage of elements and the atomic radius, when the elemental distribution in the liquid alloys is completely homogeneous and the cooling solidification rate is infinite during the preparation process. Actually, the process assumption cannot be realized. Although a previous work has already proven that the assumption does not affect the applicability of the calculated results,a slight error persists. In this work, a correction factor is introduced to improve the accuracy of the calculation method and its influencing factors are analyzed.

2. Correction method

wherem=0 or 1(ifi=j,m=0;and ifi ?=j,m=1),Riis the radius of theith atomic element atom,xiis the mole fraction of the same element, andnis the number of atomic types in the amorphous alloy.

Miracle[2]regarded solute-centered clusters as the basic building blocks of amorphous alloys and combined randomly positioned solvent atoms and medium-range atomic order solute atoms to successfully reproduce diffraction data over radial distances up to～1 nm.A large number of atomic clusters that have solute atoms as the center and are closely surrounded by solvent atoms can be formed only when the ratio of atomic bonds between solute atoms and solvent atoms exceeds the random value. This finding indicates that the atomic accumulation is not completely random,and the probability of pairing between heterogeneous atoms is relatively large. Solute and solvent elements in amorphous alloys usually have a negative mixing enthalpy, which may be the main reason for the increased bonding ratio of heterogeneous elements.

Figure 1 shows the real atomic bond proportions of Zr-Cu and Al-Mg amorphous alloys calculated using the partial coordination numbers,and the estimated atomic bond proportions were calculated using mole fraction and atomic radius.The raw data of real atomic bond proportions were derived from Refs.[10,11]and the atomic radius values were acquired from Ref. [7]. The estimated percentage of the atomic bond between two identical atoms is slightly higher than the real percentage (Figs. 1(c)-1(f)). Meanwhile, the estimated percentage of the atomic bonds between different types of atoms was lower than the real percentage(Figs.1(a)and 1(b)). This result means that the binding and pairing of the atoms were not completely random in the cooling process but were affected by the mixing enthalpy. The value of the mixing enthalpy between the main elements of the amorphous materials is usually negative but conducive to the formation of amorphous materials. In particular, the mixing enthalpy value of Zr-Cu is?23 kJ/mol and that of Al-Mg is?2 kJ/mol.[12]The negative mixing enthalpy value helps promote atoms to combine with different types of atoms to reduce the system energy.[13]Thus,for instance,the percentage ofA-Bbond in binary amorphous alloys is2xAxBRARB/(xARA+xBRB)2, and the percentages ofA-AandB-Bbonds arexAxARARA/(xARA+xBRB)2andxBxBRBRB/(xARA+xBRB)2, respectively, under completely random conditions. In practice,given the mixing enthalpy effect, the percentage ofA-Bbonds is higher than the abovementioned value and can be combined with the correction factorλto provide the expression

wherem=0 or 1(ifj=i,m=0; and ifj ?=i,m=1),λi?jis the correction factor corresponding to theith andjth atomic elements,Riis the radius of theith atomic element atom,xiis the mole fraction of the same element,andnis the number of atomic types in the amorphous alloy.

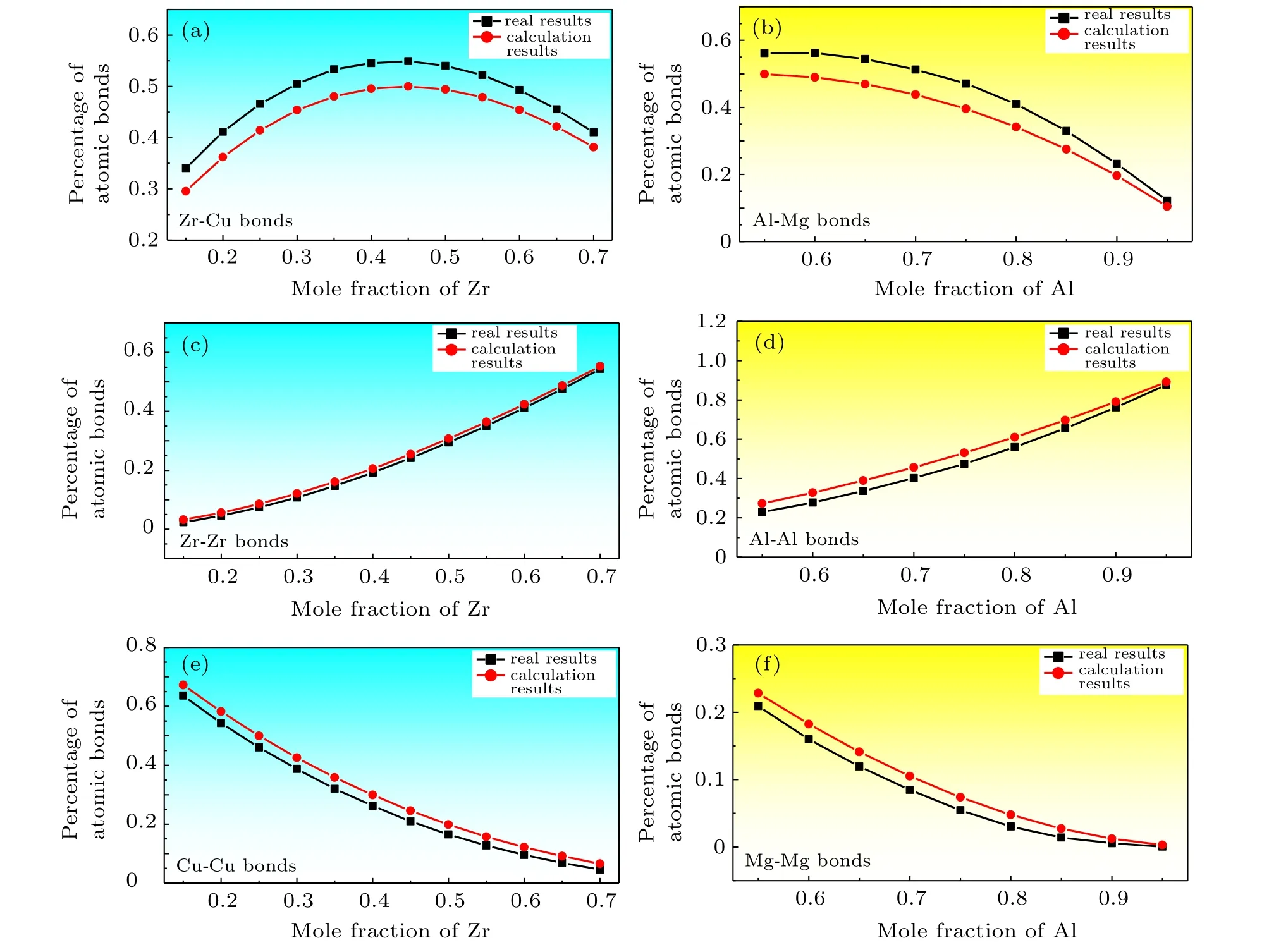
Fig.1. Real and estimated atomic bond proportions of Zr-Cu and Al-Mg amorphous alloys.

3. Results and discussion

Correction factorλreflects the tendency of binding and pairing of different types of atoms. The value ofλcan be obtained by fitting the real data using the modified computational formula of atomic bond proportions,and an increased value ofλindicates that the corresponding two types of atoms form additional atomic bonds. The adjusted results withλZr-Cu=0.1 andλAl-Mg=0.15 are presented in Fig. 2. The adjusted results are highly consistent with the actual results. Figure 3 reveals the real, estimated, and revised atomic bond proportions of various amorphous alloys. The results further prove the feasibility of the correction method.[14-21]

However, Figs. 3(e) and 3(g) show completely opposite results.[19,20]The real percentages of atomic bonds formed by different types of atoms were lower than the estimated results calculated by the completely random model. Moreover, the negative values ofλwere obtained. Analysis found that these two data sets were derived from the x-ray and neutron diffraction patterns of the amorphous alloys and suggested that the experimental samples are true amorphous alloys rather than molecular dynamics models. The experimental amorphous alloys often use pure metals as raw materials, which may not completely dissolve or become homogenous in the melting process and hence remain in the final solidification. In this case,the number of atomic bonds corresponding to the undissolved elemental metals is higher than the estimated number,and the probability of forming atomic bonds between different types of atoms decreases. In general, the atomic bond proportions calculated by molecular dynamics simulation do not show the opposite phenomenon, because the distribution of various atoms in the molecular dynamics model is uniform and devoid of the accumulation of identical atoms.

Figures 3(m) and 3(n) show the real, estimated, and revised results of the percentages of atomic bonds in Ca60Mg15Zn25.[21]These findings suggest that the revised results were unexpectedly ideal. The values of theλcorresponding to Ca-Mg, Ca-Zn, and Mg-Zn were 0.036, 0.132,and 0.024,respectively,which were proportional to the absolute mixing enthalpy values of?6 kJ/mol,?22 kJ/mol, and?4 kJ/mol,respectively. These results indicate that the matching ability of the different types of atoms increased with raised absolute value of mixing enthalpy in the identical amorphous alloys.

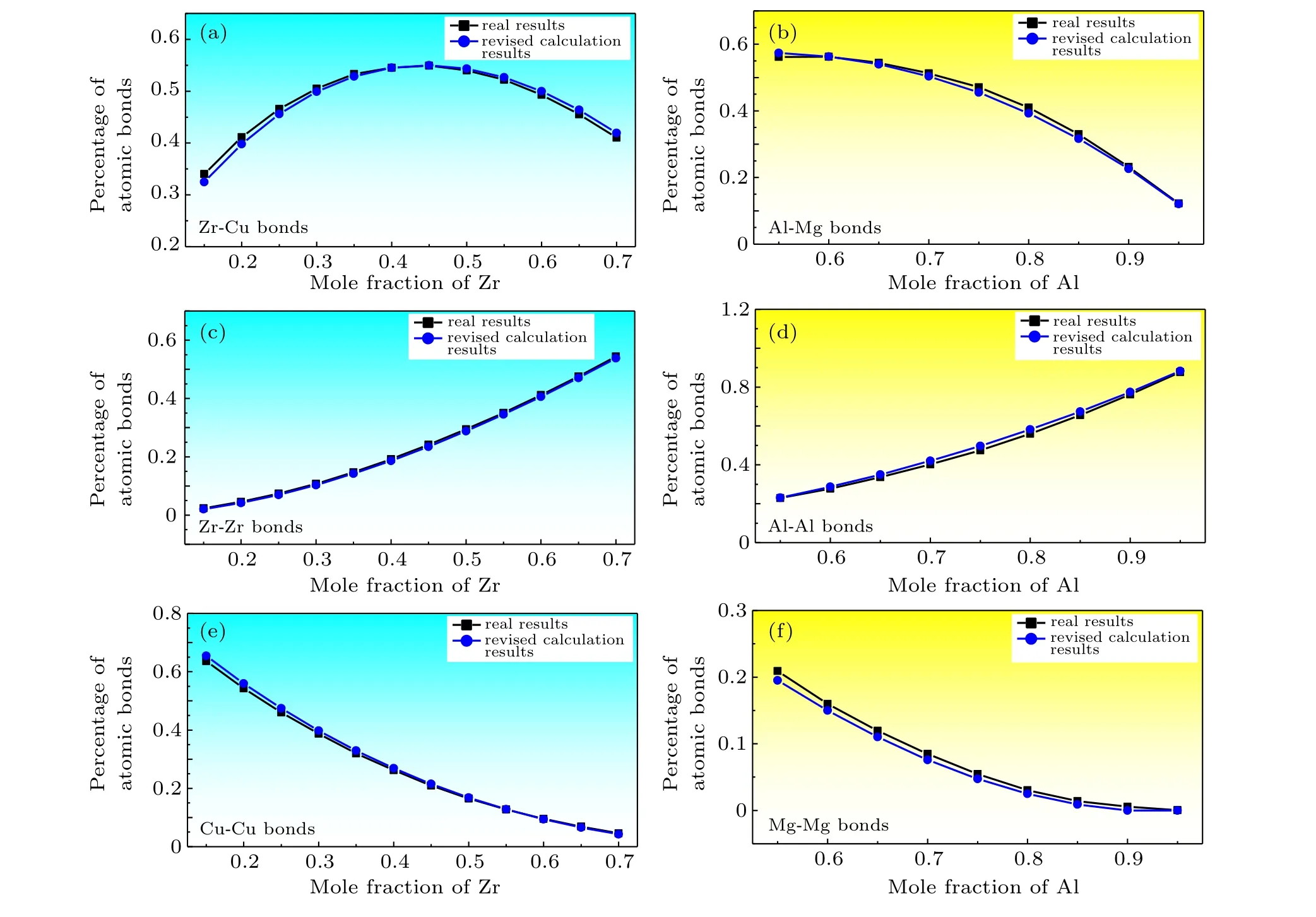
Fig.2. Real and revised atomic bond proportions of Zr-Cu and Al-Mg amorphous alloys.

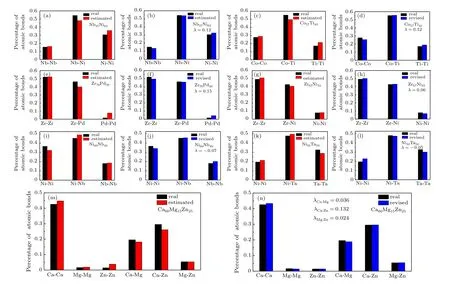
Fig.3. Comparison of the estimated and revised atomic bond proportions of various amorphous alloys.

Meanwhile, Fig. 4 shows the real atomic bond proportions of Ni80Mn20amorphous alloys with different annealing times, as well as those of Zr36Cu64amorphous alloys with different cooling rates.[22]The values ofλwere calculated by the corresponding data. It is found that the value ofλcorresponding to Ni-Mn increased with rising annealing time,and the value ofλfor Zr-Cu decreased with increasing cooling rate. These results suggest that a prolonged annealing period contributes to the bond of different types of atoms,and an increased cooling rate inhibits this phenomenon.

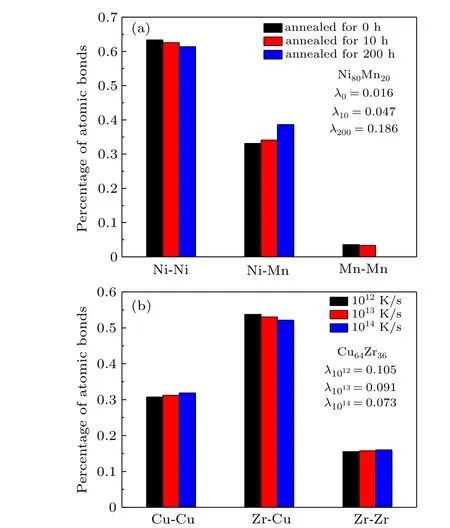
Fig. 4. Real atomic bond proportions and corresponding correction factors of (a) Ni80Mn20 amorphous alloys with different annealing times and(b)Zr36Cu64 amorphous alloys with different cooling rates.

4. Conclusion

Overall, the correction factorλreflects the tendency of binding and pairing of different types of atoms and can be used to accurately estimate the atomic bond proportions in the amorphous alloys entirely composed of metallic elements.The value ofλis proportional to the absolute value of mixing enthalpy and annealing time,as well as inversely proportional to the cooling rate during preparation. Given the correction method, the atomic bond proportions of any amorphous alloy in the corresponding system can be accurately predicted by testing several specific amorphous alloys. Therefore,a new chapter has been opened in the microstructure characterization and performance prediction of amorphous alloys.