Numerical simulation of nanosecond laser ablation and plasma characteristics considering a real gas equation of state
Qiang LIU (劉強), Qi MIN (敏琦),2,?, Maogen SU (蘇茂根),2, Xingbang LIU(劉興邦), Shiquan CAO (曹世權),2, Duixiong SUN (孫對兄),2,Chenzhong DONG (董晨鐘),2 and Yanbiao FU (符彥飆),2,?
1 Key Laboratory of Atomic and Molecular Physics and Functional Material of Gansu Province,College of Physics and Electronic Engineering,Northwest Normal University,Lanzhou 730070,People’s Republic of China
2 Joint Laboratory of Atomic and Molecular Physics,Northwest Normal University and Institute of Modern Physics of Chinese Academy of Sciences, Lanzhou 730070, People’s Republic of China
Abstract Based on the governing equations which include the heat conduction equation in the target and the fluid equations of the vapor plasma, a two-dimensional axisymmetric model for ns-laser ablation considering the Knudsen layer and plasma shielding effect is developed.The equations of state of the plasma are described by a real gas approximation, which divides the internal energy into the thermal energy of atoms,ions and electrons,ionization energy and the excitation energy of atoms and ions.The dynamic evolution of the silicon target and plasma during laser ablation is studied by using this model,and the distributions of the temperature,plasma density,Mach number related to the evaporation/condensation of the target surface, laser transmissivity as well as internal energy of the plasma are given.It is found that the evolution of the target surface during laser ablation can be divided into three stages: (1) the target surface temperature increases continuously; (2) the sonic and subsonic evaporation; and (3) the subsonic condensation.The result of the internal energy distribution indicates that the ionization and excitation energy plays an important role in the internal energy of the plasma during laser ablation.This model is suitable for the case that the temperature of the target surface is lower than the critical temperature.
Keywords: ns-laser ablation, hydrodynamic model, Knudsen layer, equation of state
1.Introduction
A ns-laser ablation has been extensively applied to the micromachining [1], pulsed laser deposition [2, 3], laserinduced breakdown spectroscopy [4, 5], and material surface treatment [6, 7] in recent years.The development of each application is closely related to the physical mechanism of the interaction between laser pulse, target and plasma.
Nanosecond laser ablation of solid targets is a complex process, including absorption of laser energy by the target,evaporation/condensation of the target surface, formation of transient plasma,expansion of plasma to surrounding gas and absorption of laser energy by plasma (the shielding effect)[8–10].In this process, Knudsen layer (KL) [11–13] and shielding effect have significant effects on the dynamic evolution of target and plasma.KL is a transient non-equilibrium layer and jump phase boundary between the vapor and condensed phase.The non-equilibrium degree is determined by the particle flow through the layer,and can be expressed as the function of the Mach number of the vapor near KL.The total particle flow through KL includes the particle flow leaving the condensed phase by evaporation and the particle flow returning to the target surface by collision from the vapor phase.At the same time, KL as the phase boundary between the condensed and vapor phase leads to the discontinuity of parameters (such as temperature, density, etc) between the target surface and the vapor phase.But KL only exists when the temperature of the target surface is lower than the critical temperature.Above the critical temperature, KL disappears and the liquid and vapor phases mix together [14].In addition, the plasma shielding effect also has a significant influence on the dynamic evolution of target and plasma.For nslaser,the plasma mainly absorbs the laser energy through the photoionization (PI) and inverse bremsstrahlung (IB) processes [15, 16], which makes the electron density and temperature increase and the laser energy reaching the target surface decrease significantly.
Up to now, many hydrodynamic models including KL and plasma shielding effect [17–24] have been proposed to simulate the interaction between ns-laser, target and plasma.However, most of the models [17, 20, 24] only consider the contribution of thermal energy and ionization energy to the internal energy of the plasma in the equation of state,ignoring the excitation energy.Some models[18,19,23]even used the ideal gas approximation of the plasma,and the ionization and excitation energies in the internal energy have been neglected.Actually, such approximation only holds when the number densities of ions in the plasma are far less than those of atoms(the average charge state is much less than 1)and most atoms are in the ground state.Unfortunately, this is not the case for laser-induced plasma [25].
In the present work, a two-dimensional axisymmetric model for ns-laser ablating the silicon target is established based on the time-dependent heat transfer equation and fluid equations.Such equations are coupled by the KL condition.The equations of state of the plasma are described by a real gas approximation,which divides the internal energy into the kinetic (thermal) energy of atoms, ions and electrons, ionization energy and the excitation energy of atoms and ions.A Gaussian laser pulse with the peak laser intensity of 5.0 ×108W cm?2,full width at half maximum of 10 ns,and wavelength of 1064 nm is selected.The Si target is in a vacuum with a pressure of5.0 ×10?4Pa.The model is valid for the case that the temperature of the target surface is less than the critical temperature.
2.Theoretical model
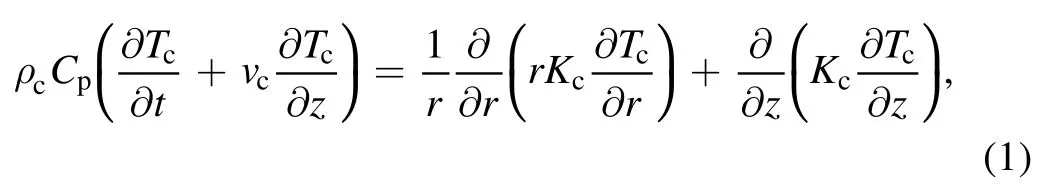
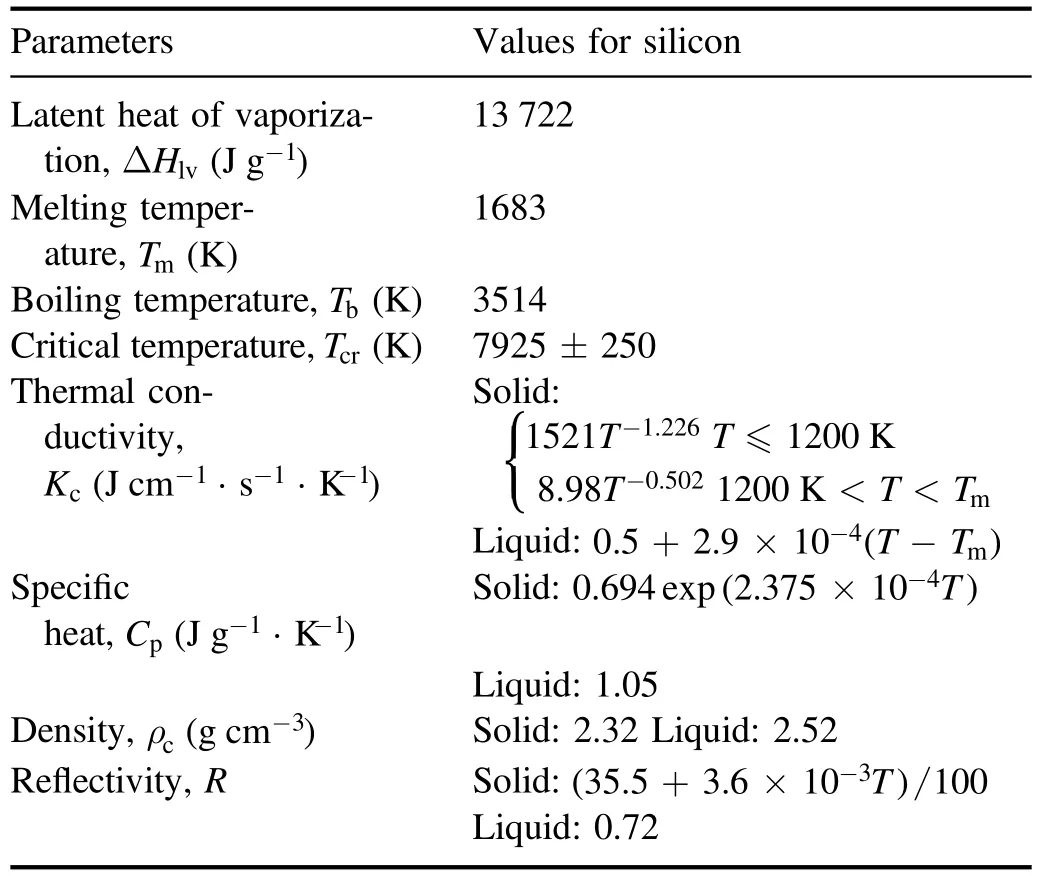
Table 1.Thermal parameters of the Si target [27, 28].
The energy transfer inside the Si target is calculated by the following heat transfer equation [22], which was solved by using an alternating direction implict scheme [26]where the subscript‘c’represents the solid/liquid medium,Tcis the target temperature,vcis the surface recession velocity.Kcis the thermal conductivity,Cpis the specific heat,andρcis the target density.The corresponding thermal parameters of the Si target [27, 28] are shown in table 1.
The initial and boundary conditions of equation (1) can be expressed as follows:
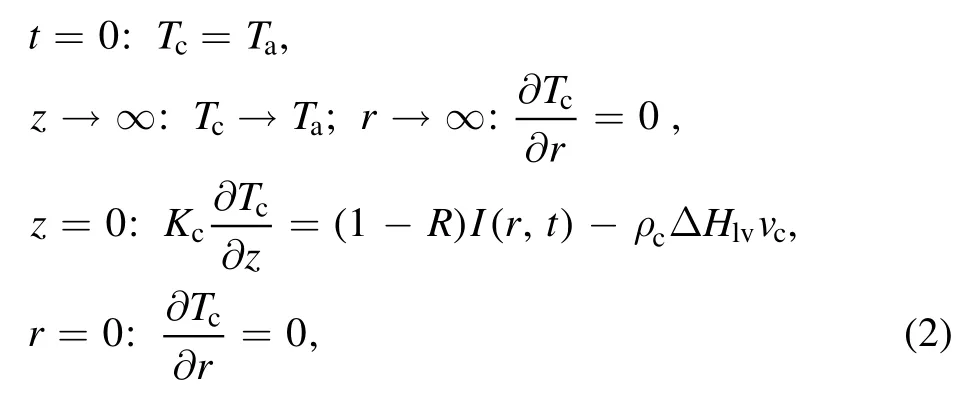
whereTais initial temperature,Ris the reflectivity of the target surface,ΔHlvis the latent heat of vaporization, ( )I r t,is the laser intensity.
The surface recession velocityvcin equation (1) can be written asWherem˙+is the mass flux of particle flow leaving the condensed phase by evaporation,which is given by Hertz–Knudsen formula [20].˙?mis the mass flux of particle flow returning to the target surface by collision from the vapor phase,which can be expressed as the function of the Mach number of the vapor near the KL, and calculated by Knight’s approach [29].
Since the density of plasma generated by ns-laser pulse is so high that the number of collisions between evaporated atoms is sufficient for hydrodynamics to apply [9], the vapor plasma flow can be described by the fluid equations mentioned in our previous work [30, 31].Electron–atom and electron–ion IB as well as PI are considered in the absorption of laser energy by the plasma, and the corresponding expressions can be found in [15, 16].

Figure 1.The temperature distributions of the Si target in r–z plane for the delay times of 13, 20, 25, and 30 ns, respectively.
In this model,the internal energy density of the plasma is given by a real gas approximation, which divides the internal energy into the thermal energy of atoms, ions and electrons,ionization energy and the excitation energy of atoms as well as ions:
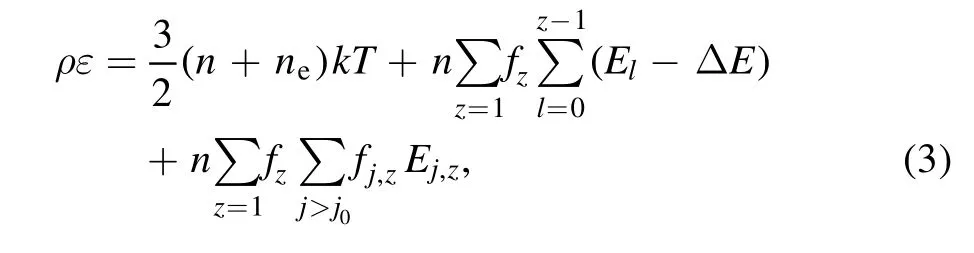
whereρεis the internal energy density,nandneare the total atomic and electron number density, respectively.Tis in degrees Kelvin,kis the Boltzmann constant.Elrefer to the ionization energy oflth ionization state, =l0 corresponds to atoms.ΔEis a correction to the ionization energy and calculated by Debye shielding.Ej z,is the excitation energies of the energy leveljwith respect to the ground state energy.j0represents the ground state of each ion.fzandfj z,are the relative ionization fractions and excitation fractions, respectively, and can be calculated by the Saha equation and Boltzmann distribution.
3.Results and discussion
3.1.Characteristic of the Si target during ns-laser ablation
The initial temperature of the Si target is 300 K.However,with the ns-laser pulse acting on the target surface, the target temperature increases rapidly.The temperature distributions of the target which located inr–zplane for different times have been displayed in figure 1.According to simulation results, the surface temperatures of the target (z=0) are always higher than the internal temperatures (z<0) at different times.When the time evolves, the range of heating region inside the target is expanded due to the thermal conduction,and the decrease rate of the maximum temperature gradually slows down.At 13 ns, the radial distribution of temperatures is consistent with the Gaussian distribution of laser intensity, and the temperature at the center of the target surface (r=0,z=0) is the highest,reaching 8120 K.At 20 ns, the radial distribution is no longer Gaussian shape, and the temperatures at the edge(r≈0.3 mm, ?1.5μm The temperature distributions of the Si target shown in figure 1 can be attributed to the combined effects of laser irradiation, heat conduction, evaporation/condensation and plasma shielding.In order to explain the influence of evaporation/condensation and plasma shielding effect on the temperature distributions of the target, the temporal evolutions of the temperature with and without plasma shielding,the Mach number of the vapor near KL, and the laser transmissivity (which is defined as the laser intensity reaching the target surface divided by the original laser intensity) at the center of the target surface (r=0,z=0), as well as the temporal profile of original laser intensity are shown in figure 2.As the original laser intensity (Io, dash line)increases, the surface temperature without plasma shielding(Ts-np,wine line)also increases.However,the time forTs-npto reach the maximum (att=16 ns) is later than that forIo(att=15 ns).After reaching the maximum,Ts-npdecreases gradually, but the decrease of temperature is slower than that of original laser intensity, which is due to the thermal inertia of the target.Therefore,an asymmetric distribution ofTs-npis caused by a symmetric laser pulse. Figure 2.The temporal evolutions of the temperature with and without plasma shielding(red and wine line,respectively),the Mach number(blue line), and the laser transmissivity (black line) at the center of the target surface (r=0, z=0).Dashed line indicates the temporal profiles of original laser intensity. In figure 2,the Mach number(M,blue line)of the vapor near KL can indicate the evaporation/condensation process and the non-equilibrium degree of KL.Here,=M1 corresponds to the sonic evaporation, the total particle flow through the KL is the highest, and the evaporation process takes place under a strongest non-equilibrium.The condition of =M0 and the surface temperature is less than the boiling point, means that evaporation has not started yet.But the condition ofM=0 and the surface temperature is larger than the boiling point, means that the total particle flow through KL is zero, and the particle flow leaving and returning to the condensed phase is in equilibrium.When 0 According to the Mach number in figure 2, the laser ablation process includes three stages.The first stage is from 0 to 9 ns, the surface temperature with plasma shielding (Ts,red line) grows monotonically but it does not reach the boiling point.This means that the evaporation process has not yet occurred, so the Mach number is always 0, and the laser energy can reach the target surface completely without absorption.The second stage is from 9 to 15 ns, in whichTscontinues to rise from 10 to 13 ns and is higher than the boiling point,reaching a maximum of 8120 K at 13 ns.At the same time, both the Mach number and laser transmissivity(black line) are equal to 1, which means that there is a sonic evaporation and the plasma has not yet formed.At 14 ns, the Mach number is still equal to 1,butTsand laser transmissivity decrease, which indicates that the vapor breakdown occurs at about 14 ns and forms a plasma,and a part of the laser energy is absorbed by the plasma, which reduces the laser energy reaching the target surface.At 15 ns,the Mach number equals 0.1,which corresponds to subsonic evaporation.The subsonic condensation (M< 0) occurs at stage 3, 16 ns≤t≤30 ns.At this stage, the profile ofTshas a downward trend as a whole, but increases slightly between 17 and 21 ns, which is due to the energy of particles returning to the target surface compensates for the energy loss caused by heat conduction.Except for the first stage, the surface temperature in the second and third stages is quite different when plasma shielding is considered or not. At 20 and 25 ns, the radial distributions of the temperature, Mach number and laser transmissivity at the target surface (z=0) are shown in figure 3.It can be seen that the parameters’distributions of the central region(? 0 .25 mm≤r≤0.25 mm) and the edge region(? 0 .5 mm≤r< ?0.25 mm and 0.25 mm Figure 3.The radial distributions of the temperature (red line), Mach number (blue line) and laser transmissivity (black line) at the target surface (z=0) at 20 and 25 ns.Dashed line indicates the spatial profiles of original laser intensity at 20 and 25 ns, respectively. Figure 4.The temperature distributions of the Si plasma in r–z plane for the delay times of 15, 20, 25, and 30 ns, respectively. Figure 5.The (a) density and (b) axial velocity distributions of the plasma at =r 0 along the z-axis for the delay times of 15, 20, 25 and 30 ns, respectively. The two-dimensional contour distributions of the Si plasma temperature inr–zplane at 15, 20, 25 and 30 ns have been shown in figure 4, respectively.It is clearly seen that the plasma has been formed at 15 ns and the maximum temperature has reached 1.4 eV.Therefore, the subsequent laser pulse will be absorbed by the plasma, which makes the plasma temperature continue to rise and the laser energy reaching the target surface will be reduced.At 20 ns, due to the continuous input of laser energy, the maximum temperature of the plasma reaches 3.9 eV.At 25 and 30 ns, the maximum temperatures decrease slightly compared with that at 20 ns, and the radial and axial dimensions of the plasma increase significantly.The distribution of the target temperature in figure 1 is closely coupled with the distribution of the plasma temperature in figure 4.On one hand, the laser intensity acting on the target surface after being absorbed by plasma should be considered in the boundary condition(equation(2))of the heat transfer equation.On the other hand,the parameters of target surface provide the boundary conditions for the fluid equations by the discontinuity of KL.In addition,the absorption of laser pulse by plasma represents an important coupling,which is related to both plasma expansion and laser-target interaction.The laser energy will be greatly attenuated before reaching the target,resulting in low heating and evaporation efficiency of the target. The density and axial velocity distributions of the plasma at =r0 along thez-axis for the delay times of 15,20,25 and 30 ns are shown in figure 5.During the period of ns-laser ablation, especially when the delay time is less than 15 ns, a large number of ablated silicon materials enter into the plasma domain, thus forming a high-density region near the target surface (figure 5(a)).Such dense and hot plasma expands in vacuum at a speed of 10–30 km s?1along the direction perpendicular to the target surface (figure 5(b)).Due to the free expansion of plasma in vacuum and the sharp decrease of laser energy reaching the target surface after 15 ns (figure 2),the plasma density decreases obviously as functions of time and distance from the target surface.The axial velocity increases gradually along thez-axis, reaches the maximum and then remains stable,and finally decreases rapidly to zero.It is worth noting that the axial velocity near the target surface decreases as a function of time and becomes negative at 20 ns(?205 m s?1),25 ns(?1416 m s?1)and 30 ns(?2562 m s?1).This is consistent with the distribution of the Mach number in figure 2, and indicates that the pressure of plasma near the target surface exceeds the saturated vapor pressure of target surface, which makes the vapor plasma move back towards the target and form condensation.In this model,the saturated vapor pressure of the target surface is calculated by the Clausius–Clapeyron equation [20]. As functions of delay times, the energy density distributions of the internal energy, thermal energy, ionization energy as well as the energy of electronic excitations are shown in figure 6(a), and the distributions of the Si I-III ions as well as the average charge state in the plasma are shown in figure 6(b),respectively.From 15 to 17 ns,the internal energy of the plasma is mainly contributed by the thermal energy of atoms and electrons, as well as the energy of electronic excitations of atoms(figure 6(a)).This is because the particles in plasma are mainly neutral atoms(figure 6(b)),and most of these atoms are in the excited state under the assumption that the energy level population satisfies the Boltzmann distribution(the plasma temperature has reached about 1.7 eV in this time period).As time evolves, the internal energy density decreases with the decrease of plasma density, but the proportion of ionization energy in the internal energy increases with the increase of the fractions of Si II and III ions.The results of internal energy distribution in figure 6(a) indicate that the contribution of the energy of electronic excitations must be considered in the internal energy of plasma during laser ablation, that is, the real gas approximation(equation(3))should be used to describe the equation of state of plasma. Figure 6.The distributions of(a)the internal energy,thermal energy,ionization energy as well as the energy of electronic excitations of the plasma,and(b)the ion fractions as well as average charge state of Si in the plasma as a function of delay time at r=0, z=0,respectively. Figure 7.The spatial distributions of the internal energy, thermal energy, ionization energy, and energy of atomic excitations at 30 ns,respectively. Moreover,the spatial distributions of the internal energy,thermal energy, ionization energy, and energy of atomic excitations at 30 ns are shown in figure 7.The distribution of the energy of atomic excitations inr–zplane is consistent with that of neutral atoms in this plane.This result further confirms our conclusion that the contribution of the energy of electronic excitations to internal energy during laser ablation cannot be ignored. Figure 8.The distributions of the plasma temperature based on three different equations of state as a function of delay time at r=0, z=0,respectively.Case I is real gas approximation,Case II is ideal gas approximation and Case III is ideal gas approximation combined with ionization energy. Finally, to explain the influence of the equation of state on the plasma parameters, we calculate the plasma temperature based on three different equations of state, which are real gas approximation (equation (3), Case I), ideal gas approximationCase II) and ideal gas approximation combined with ionization energyCase III).The distributions of the plasma temperature as a function of delay time atr=0,z=0 are shown in figure 8.It should be noted that the plasma temperature calculated by ideal gas approximation (Case II) is much higher than that of the real gas approximation (Case I), since the supplied energy goes entirely into the thermal energy, while in the real gas approximation, most of the energy goes into the ionization and atomic excitation, thus reducing the plasma temperature.Combined with the results of figures 6–8, we predict that the equation of state of plasma needs to be described by a real gas approximation during ns-laser ablation, and this prediction is consistent with the conclusion in [25].In addition, the applicability of the real gas approximation also needs to be verified by experimental results.In our previous work [32],we measured the temperature and electron density of Si plasma using time-resolved spectra, and obtained a plasma temperature of 2.75 eV at 30 ns.It can be seen from figure 8 that the plasma temperature calculated by the real gas approximation is 2.71 eV at 30 ns and most consistent with the experimental result.Unfortunately, we did not get the spectrum before 30 ns,so the experimental result at only 30 ns cannot fully verify the applicability,and we need to get more experimental results in the future. In summary, a two-dimensional axisymmetric model for nanosecond laser ablation considering surface evaporation/condensation and plasma shielding effect is developed.The equations of state of the plasma are described by a real gas approximation, which divides the internal energy into the thermal energy of atoms,ions and electrons,ionization energy and the excitation energy of atoms as well as ions.The spatial-temporal distributions of the target temperature, Mach number of the vapor near KL, laser transmissivity, plasma temperature and density,and internal energy of the plasma are given.It is found that the laser ablation process consists of three stages: (1) the target surface temperature increases continuously and does not exceed the boiling point at the beginning of laser ablation; (2) the sonic and subsonic evaporation occurs in the middle stage of laser ablation; (3) the laser energy is absorbed by the plasma and subsonic condensation occurs.The composition of internal energy of the plasma during laser ablation is analyzed, a key conclusion that the contribution of the energy of electronic excitations to internal energy during laser ablation cannot be ignored is obtained.The model is valid for the case that the temperature of the target surface is lower than the critical temperature. Acknowledgments This work is supported by the National Key Research and Development Program of China (No.2017YFA0402300),National Natural Science Foundation of China (Nos.11904293, 12064040 and 11874051), the Science and technology project of Gansu Province (No.20JR5RA530), the Young Teachers Scientific Research Ability Promotion Plan of Northwest Normal University(No.NWNU-LKQN-18-32),and the Funds for Innovative Fundamental Research Group Project of Gansu Province (No.20JR5RA541).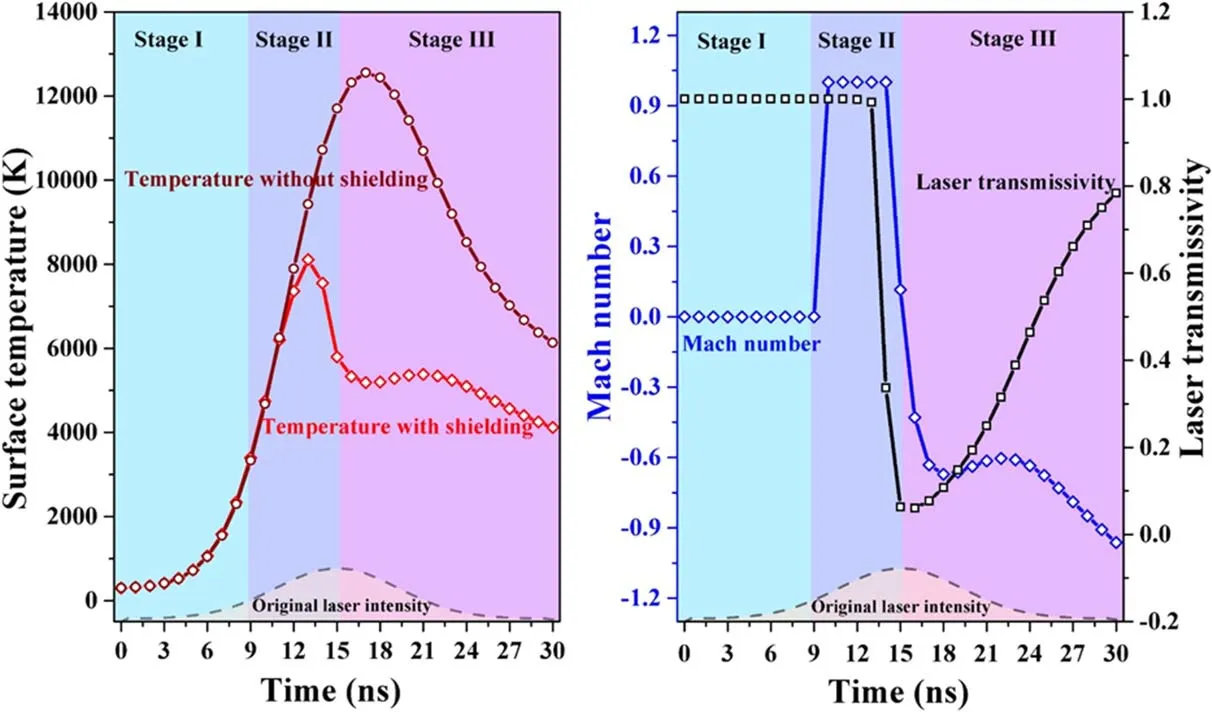

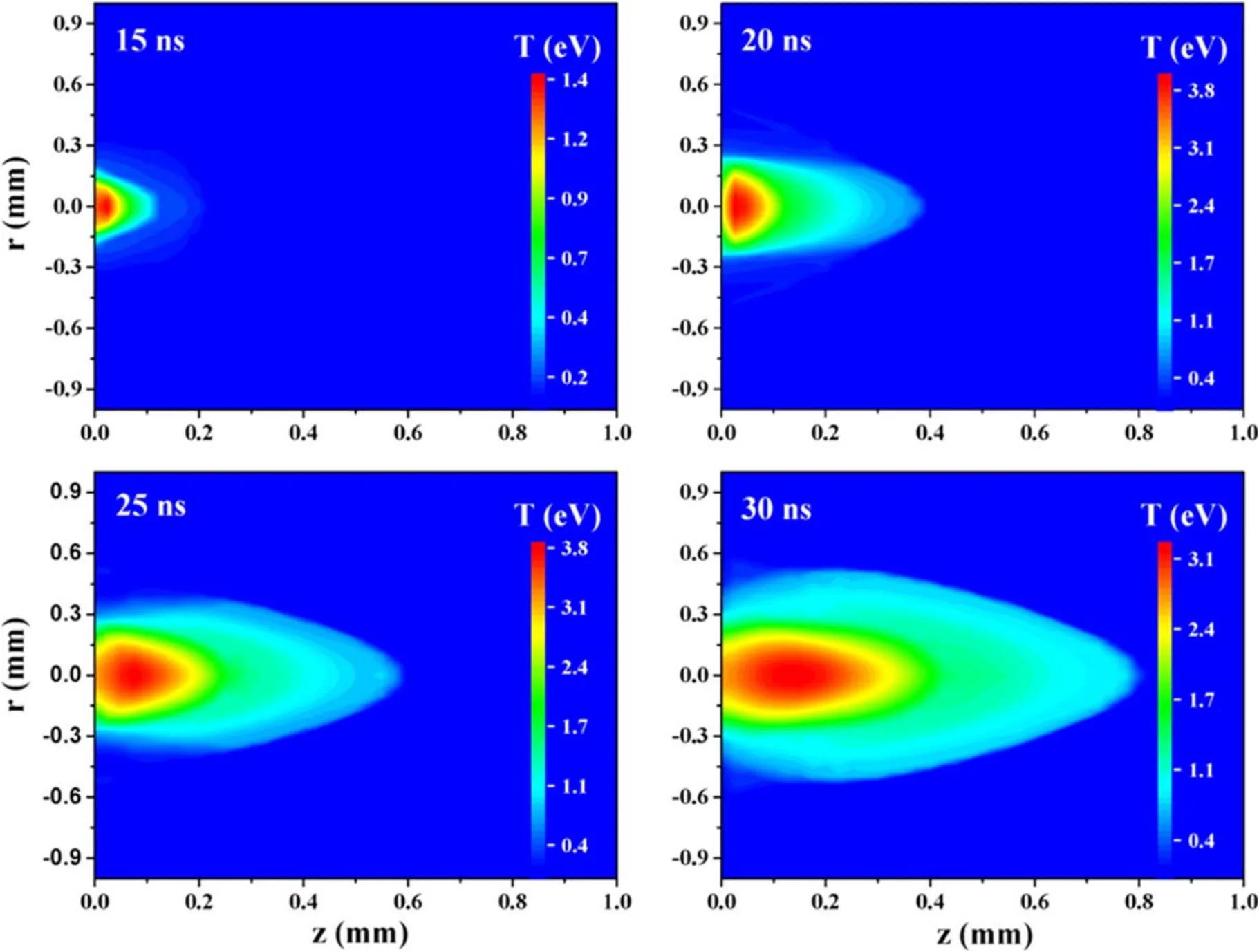

3.2.Characteristic of the vapor plasma during ns-laser ablation
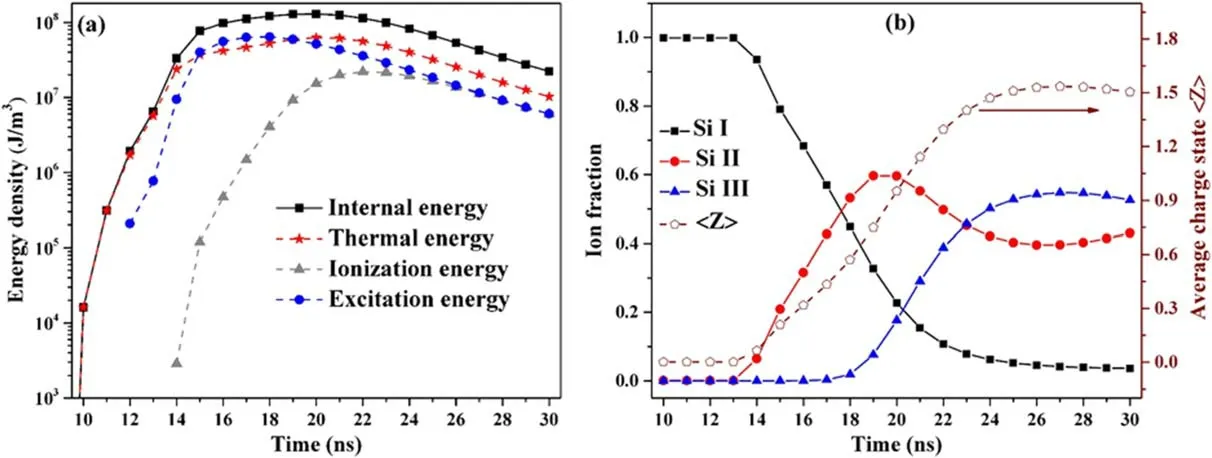

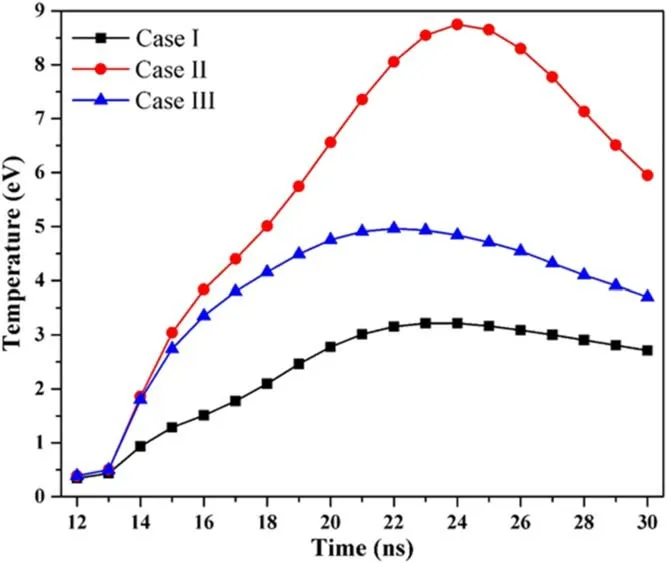
4.Conclusions
 Plasma Science and Technology2021年12期
Plasma Science and Technology2021年12期
