Spin-orbit stable dirac nodal line in monolayer B6O
Wen-Rong Liu(劉文榮) Liang Zhang(張亮) Xiao-Jing Dong(董曉晶) Wei-Xiao Ji(紀(jì)維霄)Pei-Ji Wang(王培吉) and Chang-Wen Zhang(張昌文)
1School of Physics and Technology,Institute of Spintronics,University of Jinan,Jinan 250022,China
2School of Physics and Physical Engineering,Qufu Normal University,Qufu 273100,China
Keywords: monolayer B6O,Dirac nodal line,two-band tight-binding model
The 2D materials[1-4]have attracted much attention because of their rich properties. Among the rest, topological semimetals (TSMs) are a class of systems in which the conduction and valence bands cross each other within the Brillouin zone, while they are robust. These excellent properties provide a unique site for singular phenomena derived from band topology.[5,6]DNL semimetals,[7-19]as one of the TSMs,connect the gapless and gapped phases and can be tuned to a variety of other topological phases, such as topological insulators,Dirac and Weyl semimetals.[20-27]It has become a new class of quantum materials that are more promising for scientific research. Many excellent physical properties have been obtained in these nodal line materials, including Friedel oscillation, nondispersive Landau energy level,[28]and specific long-range Coulomb interactions,[29]etc., which pioneers a new path for Dirac materials in future low dissipation device applications. These proposals,however,are dependent on the effect of spin-orbit coupling(SOC):when SOC is considered,the structure of node line will be broken,and there is a sizable gap at the intersection of conduction band and valence band.Until now,PbTaSe2,a nodal line semi-metallic structure with strong SOC,is only experimentally confirmed.[12]
The fundamental conceptions of Dirac, Weyl and DNL semimetals are also suitable for use in 2D materials.Some current theoretical works.[30-32]illustrate nodal wire-band crossing with weak SOC.However,similar to the three-dimensional(3D) case, the nodal line band present in these materials is broken when SOC is turned on. It is reported that 2D DNL fermions with SOC in single-layer Cu2Si have been realized experimentally.[33]Interestingly, a recent article[34]summarizes and classifies all possible structures with cross properties in 2D noncentro-symmetric systems with SOC and time inversion invariance. According to the prediction of this research,when a material has appropriate geometric symmetry,the node line band crossing is stable for SOC.In fact,weak SOC materials,such as Be2C,BeH2,[35]and Na2CrBi trilayer[36]are proposed as intriguing 2D nodal line materials.Therefore,finding 2D materials with high-stable nodal line bands is a more nontrivial work.
In this paper, we demonstrate that monolayer B6O(Figs. 1(a) and 1(b)), which has remarkably energetic stability and positively dynamical stability, possesses a nodal line band structure that maintains robust even if considering the effect of SOC. Compared with the single Dirac point of other 2D allotropes, the band structure of B6O is characterized by elliptical DNL, and its Fermi velocity is 106m/s, which is as the same as that of graphene. The nodal line band crossing is further explained by combiningk·pmodel calculation with symmetry analysis. Also, B6O/h-BN superstructure is proposed to realize DNL feature of monolayer B6O in experiments. Our results not only reveal a new DNL fermion of matter, but also offer promising material platform for realizing novel low-dissipation devices.
All the structural and electronic properties are calculated by using the projector augmented wave(PAW)method[37]implemented in the Viennaab initiosimulation package(VASP)code.[38,39]The Perdew-Burke-Ernzerhof (PBE) form of the generalized gradient approximation (GGA) exchangecorrelation functional[40]is adopted, while the more accurate electronic band structure is obtained by HSE06[41,42]hybrid functional. The wave functions of all systems are expanded by using a plane wave basis with a cut-off energy of 550 eV,and the Brillouin zone sampling grids are set to be concentrated enough to guarantee convergence. The maximum force is less than 0.01 eV/°A during optimization. The vibrational spectrums are simulated by using DFT perturbation theory as implemented in the PHONOPY code.[43]The 3D energy band structure of monolayer B6O is obtained from the postprocessing maximum localized Wannier Hamiltonian derived from the code of WANNIER90.[44-46]

Fig.1. (a)and(b)The top and side views of monolayer B6O with lattice vectors a(~2.88 °A)in the x-y plane. The unit cell is marked with a rhombus.(c)The phonon spectrum of B6O.
Monolayer B6O has a hexagonal configuration with three different types of atoms in a unit cell and shares the space groupP6/mmmsymmetry, as illustrated in Fig. 1(a). The outmost-layer B1atoms possess graphenelike plane,while the second kind B2, accompanied with oxygen, banked up between top and bottom B1planes, forms a pillar that hold two B1layers. There are three kinds of bond lengths, which are labeledd1,d2,andd3,as shown in Fig.1(b). Thed1=1.66 °A is the length of the outmost graphene-like layered bonding,which is formed by two B1atoms close to sp2hybridization and the value ofd1is close to that of graphene. All the other B2atoms form a bond length,d2=1.91 °A,whiled3=1.36 °A is along for B2-O-B2pillar. The chemical bonding character of B6O can be illustrated by the electron localization function(ELF)in Fig.2. One can see that ELF is situated on the area in the middle of the B1-B1bonds within the flat hexagonal plane (Fig. 2(a)), whereas no electron localization occurs in between B1-B2atoms (Fig. 2(b)), suggesting the ionic bond character along B-O bonding. Similar results are found for B2-O-B2bonding. Additionally,the ELF plots for the sliced planes are shown in Figs.2(d)-2(f),where a high ELF distribution(0.75)is centered at the middle of B1-B1and B2-O-B2bonding, suggesting a very strong covalent bond. While for the sliced plane in Fig.2(e),the ELF equals to 0.4,suggesting partially ionic bond,which is consistent with the Bader charge analysis.[47]Further calculation and analysis show that the column composed of B2-O-B2has an average of 0.85 electrons transferred to its adjacent B1,i.e.,B2atoms act as an electron supply source to transfer electrons to the unoccupied state of sp2in plane, so that the stability of B6O is significantly enhanced. This mechanism is similar to the boronrich borides MB2or MB4,where B atoms form a hexagonal lattice like to graphene and interact with triangular metal lattice.[48]Therefore monolayer B6O is ionic,consisting of graphenelike plane and B2O pillars.
Structural stability of B6O can be further evaluated by the formation energy asEcoh=EB6O-6EB-1/2EO2,whereEB6Ois the total energy of B6O,EBandEO2is the energy of B atom and oxygen, respectively. The relative energy is -5.13 eV/atom, which is close to that of other boronbased allotropes such as B2S3(-4.9 eV/atom)[49]and B2S(-5.3 eV/atom).[50]The dynamical stability of B6O is also checked from the vibrational spectrum,as shown in Fig.1(c).There is no appreciable imaginary frequency in the phonon energy spectrum, establishing the dynamically structural stability of B6O.That is to say,when the lattice vibration is normal,B6O can maintain its basic crystal structure. We also calculate the elastic constants and find thatC11,C12,C22, andC66are 236.02 N/m, 231.25 N/m, 231.28 N/m, and 104.76 N/m,respectively.These values content the mechanical stability criteria(C11×C22-C222>0,C66>0),which illustrates that B6O has good mechanical stability and can resist small deformation. Throughab initiomolecular dynamics simulation, after heating to 300 K in a time step of 1 fs, B6O still maintains its basic crystal structure, small thermal oscillation and no obvious structural collapse. All these results illustrate that monolayer B6O has excellent thermostability and can retain its structural integrity at room temperature.

Fig.2. (a)Top view and(b)side view of the electron localization function of monolayer B6O with isovalue 0.8. (c)The different cutting planes for ELF.The ELF of plane cut along the olive dotted line(d),along the orange dotted line(e)and along the yellow solid line(f).
Figure 3(a) presents the band structure along theM-ΓK-Mpath for monolayer B6O.It portrays the nodal line band structure, and although SOC is considered, the energy band structure remains stable due to its ?MZspecular reflection symmetry(Fig.1(b)).Interestingly,the bottom of conduction band and the top of valence band cross near theKpoint and form a typical DNL.In order to confirm whether single-layer B6O is a real node line crossing or an anti-crossing structure with small energy separation,we use a theoretical model mentioned in recent research[34]to classify the band crossings in 2D systems. According to the theoretical analysis,if(i)the 2D plane has mirror reflection symmetry,and(ii)the two crossed bands have different mirror eigenvalues,it can be explained that the nodal semi-metallic state of 2D material will be stable.
For monolayer B6O in Fig.1(a),it is unchangeable under the mirror reflection aboutx-yplane,so it meets the situation described in condition(i). In this respect, the Hamiltonian ?Hshould commute with the mirror reflection operator ?MZ

Obviously, ?MZdoes not change the 2D momentumk,demonstrating that the energy eigenstates for the crystal momentumkare eigenstates of ?MZ. Due to the eigenvalue spectrum of ?MZis discrete, the continuous change of energy eigenstates as a function ofkin an energy band cannot change the eigenvalue of ?MZ, so each energy band of ?Hhas a well-defined mirror eigenvalue.
We now take the mirror eigenvalues of DNL into account,which attracts our interest. As can be seen from Fig.3, there are two crossing bands interacting along the high symmetryΓ-K-Mline in momentum space. Contributions of different orbits are represented by the orbital-projected density of states(DOSs). Two bands close toEForiginate from the B-pzorbital,linearly crossing each other,then the charge carriers can be characterized by massless Dirac fermions. This is similar to the most other 2D lattices with a Dirac point, such as Mn-DCA,[51]while the px/pyatomic orbitals only play a role in the energy bands. Obviously,when there is no symmetry protection,the two cross energy bands will interact which results in opening of the band gap. In order to check whether the two bands meet condition(ii),rough information of the wave function characteristics of the two bands is required, because the mirror eigenvalues may be discontinuous, and the mirror eigenvalues of each band can be determined to the wave functions. In the reciprocal space ofP6/mmm,high-symmetry lineΓ-Kpossess a littleD3hpoint group,including a twofold rotation axeC2yand threefold rotation axeC3z. In this respect,theKpoint is just the time-reversal-symmetry(T)partner in momentum space. The algebraic relationship within these generators should be written as

Here, the occupied and unoccupied low-energy bands atKpoint are doubly degenerate. Making use ofD3hgroup analysis, we find that irreducible representations (IRs) of pzband nearKpoint areE′andE′′, respectively. According to Eqs. (1)-(3), the whole BZ is invariant for ?MZand at anyKpoints, the eigenvalues ofC3zandC2yof all bands keep their signs unchanged. Since the IRsE′andE′′do not couple with each other,a DNL forms centeredKpoint,which will be discussed further with a theoreticalk·pmodel later.

Fig.3.(a)Orbital projected band structure of B6O.The orbital contribution is drawn in different colors,and the spot size represents its weight. The green,yellow and purple dots denoted the pxy, pz, and s orbitals of boron, respectively. (b)Density of states,where the blue,red and black lines represent the contributions of B atoms,O atoms and the total contribution,respectively.
To confirm this expectation of B6O,we propose 3D band dispersion based on B-p orbit by constructing tight bound Hamiltonian from MLWFs.[52]Figure 4(a) displays the calculated MLWF and DFT band structures, which in perfect agreement with DFT results, further confirming the accuracy of our B6O orbital component analysis. As a consequence,an entire elliptical DNL centered atKpoint can be obtained,see Fig. 4(b). It is clearly different from conventional Diraccone materials with a discrete DP nearEF. In order to visually display the band touching, we further perform a scan around crossing point D1alongΓ-Kdirection. The linearly dispersed B-pzband crosses each other, forming a serial of DPs with a tip to tip. Similar results are observed forK-Mdirection for B6O.Noticeably,though 3D DNL state has been observed experimentally,DNL in 2D boron-based sheet is rarely reported.The intriguing point of B6O band structure is that the band crossings in MS form a closed DNL because of the coexistence of time reversal and inversion symmetry.
From the crossing point with linear bands of B6O,we estimate the Fermi velocity(vF),by a linear fitting of DFT results.vFcan be understood as the transmission velocity of massless Dirac fermions,and the calculation formula is expressed as
wherektis the total number of points fromΓtoM,Δkis the number ofKpoints on a certain energy band taken betweenΓtoM,ΔEis the energy difference of this energy band,andais the lattice constant of structure.
We find that the radial velocities of the Dirac point are in the range of 0.54×106-0.63×106m/s,which is comparable to the value 0.82×106m/s in graphene. It is the ultrahigh Fermi velocity of B6O that is advantageous for building highspeed electronic devices such as field effect transistor.
Now, we discuss the forming mechanism of DNL by inferring an effective low-energyk·pmodel. As a general rule,a two-band Hamiltonian capturing the band crossing is able to be written as

wheredi(k),(i=1,2,3)is real function ofk(kx, ky, kz).σ0andσ1,2,3are the 2×2 unit matrix and Pauli matrices characterizing the space of two bands, which are mainly from B-p orbitals in B6O. In the space groupP6/mmm, thekis not an invariant point underPorT, but theTPsymmetry keeps theKpoint invariant,and it commutes with all generators. So we can write downPT=κ,whereκis the complex conjugation in a proper orbital basis. Here,the spin and orbital part of the electronic wave function are decoupled. Therefore, for each spin channel,all crystalline symmetries are retained separately as for non-spin particles. By the symmetry analysis, the two crossing bands inkz=0 plane have opposite eigenvalues ofMz. Along theΓ Kdirection, these two bands with the same eigenvalues ofC2yand opposite eigenvalues ofMx. Thus,the representation matrices of these generators requires that

Thus,B6O forms a DNL whenM/A >0.
The effects of HSE06 on band structure of B6O are further examined. We find that the band structures alongΓ-K-Mline at HSE06 level are similar to that of PBE level, where two crossing bands linearly remains atEF. Although the PBE underestimates the band gap atΓpoint, the fact that HSE06 method gives the same DNL strengthens our understanding of the effectiveness of B6O band structure, which presents an ideal material for practical applications. In 2016, Fanget al.[53]reviewed the theoretical research progress of nodal line semimetals, in which the explicit form of topological invariants of each symmetric group is discussed by analyzing the wave function on Fermi surface. Zhanget al.[54]also found that the formation mechanism of Tl2Nb2O6.5triply-degenerate nodal point can be well explained byk·pmodel. We believe our work can further promote the progress of research on DNL in 2D materials.
Now, we consider the stability of the nodal line band in the case of symmetry breaking. When we break theC3rotational symmetry, the nodal line is still robust owing to theMzmirror symmetry. On the contrary,when we break theMzmirror symmetry,the node lines not any more exist stably and may evolve into Dirac points or anti crossing structures. If some points on the nodal line become vestigial owing to the residual symmetry after the destruction ofMzmirror symmetry,the nodal line structure turns into Dirac points.In this case,B6O hasMxmirror symmetry,which can guarantee the degeneracy on theMxmirror invariant line. However, as shown in Fig. 1(b), theK(K′) point is not on theMxmirror symmetry line along theΓ-Mline in the momentum space,so the nodal line energy band crossing becomes a Dirac point band structure.
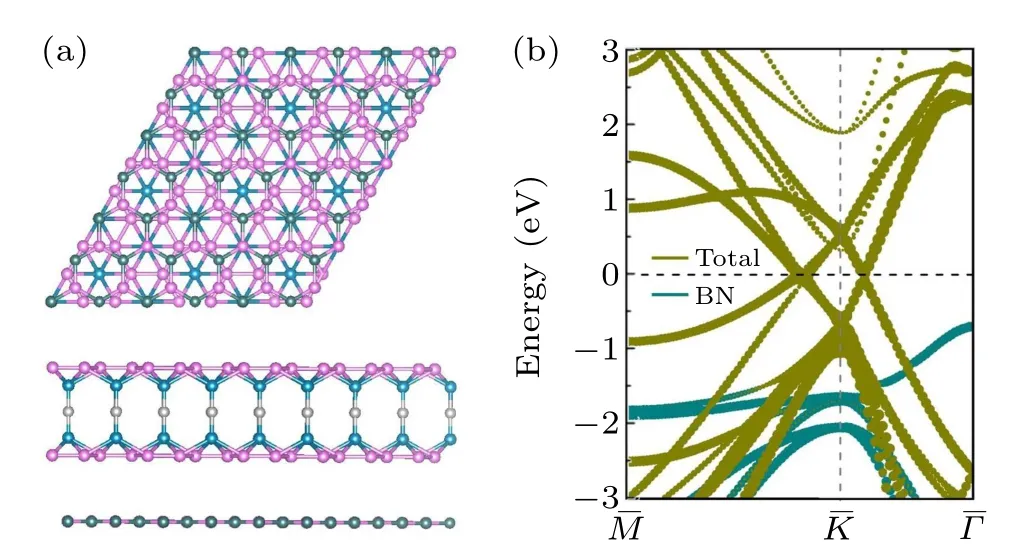
Fig. 5. (a) Top and side view of the epitaxial growth of B6O on h-BN substrate. (b)The corresponding energy band structure without SOC.The green and blue green dots are mainly from B6O and h-BN,respectively.
It is inevitable that the 2D lattice grows on the substrate,which will break the spatial symmetry of B6O, resulting in a gap in the energy bands of DNL. However, the Dirac points can be maximally preserved due to the weak interface interactions in between two sublattices. For instance, ARPES measurements do not give any characteristics about the gap opening of NL dispersion in 2D Cu2Si.[33]From the perspective of practical applications, the inherited quantum transport in Dirac materials is more fascinating because it is less vulnerable to symmetry breaking. As a matter of fact, Dirac point resides only in a free-standing graphene owing to symmetry protection. When graphene is deposited on substrate,the spatial symmetry of the two carbon atoms is broken,which leads to the opening of the gap in graphene. However,the quantum transport which is in graphene, including half-integer quantum Hall effect,[55,56]fractional QHE,[57]and ultra-high carrier mobility,[58]remains in graphene deposited on multifarious substrates. Consequently, we deduce that the quantum properties of NL materials can be maintained in B6O-based heterostructure (HTS) so long as the space symmetry is preserved to a large extent. To confirm this, we put B6O on h-BN substrate to construct B6O/h-BN HTS, which is illustrated in Fig. 5(a). Structural optimizations demonstrate that the layer spacing between B6O and h-BN substrate is 3.18 °A with a weaker binding energy of 34.6 meV,indicating the existence of van der Waals interaction. Figure 5(b) shows the band structure of B6O/h-BN in the energy range of-3 eV to 3 eV,in consistent with that of monolayer B6O.Also,the DNL fermions aroundKpoint keep well, only a tiny band gaps (a few 0.23 meV)are opened due to the symmetrical characteristic broken.
In summary,we predicted the DNL phase in 2D B6O allotrope based on first-principles calculations and TB model,which has an outstanding energetic stability and superior dynamical stability. It possesses an elliptical DNL fermion,with a Fermi velocity of 106m/s perfectly matched the order of magnitude of graphene. A two-bandk·pmodel is constructed to explain the formation mechanism of DNL in B6O. It is worth mentioning that Anosha Rubabet al.[59]reported that borophene is a perfect Dirac material. Its large surface area,high Young’s modulus and extremely high Fermi velocity make it applicable to sensors,electronics and energy converters. In 2019, Zuoet al.[60]also found that time reversal symmetry and mirror reflection symmetry can protect the nodal line inβ-boron sheet, and a nanodevice that can manipulate and control the nodal line has been proposed. These findings have opened up a new path for the realization of novel high-speed and low-power devices,and 2D B6O may be a new platform for the development of nano-devices in the future.
Acknowledgments
Project supported by Taishan Scholar Program of Shandong Province, China (Grant No. ts20190939), Independent Cultivation Program of Innovation Team of Jinan City(Grant No.2021GXRC043),and the National Natural Science Foundation of China(Grant Nos.52173283 and 62071200).
- Chinese Physics B的其它文章
- Measurements of the 107Ag neutron capture cross sections with pulse height weighting technique at the CSNS Back-n facility
- Measuring Loschmidt echo via Floquet engineering in superconducting circuits
- Electronic structure and spin-orbit coupling in ternary transition metal chalcogenides Cu2TlX2(X =Se,Te)
- Characterization of the N-polar GaN film grown on C-plane sapphire and misoriented C-plane sapphire substrates by MOCVD
- Review on typical applications and computational optimizations based on semiclassical methods in strong-field physics
- Quantum partial least squares regression algorithm for multiple correlation problem

