Neural-mechanism-driven image block encryption algorithm incorporating a hyperchaotic system and cloud model
Peng-Fei Fang(方鵬飛) Han Liu(劉涵) Cheng-Mao Wu(吳成茂) and Min Liu(劉旻)
1School of Automation and Information Engineering,Xi’an University of Technology,Xi’an 710048,China
2School of Electronic Engineering,Xi’an University of Posts&Telecommunications,Xi’an 710061,China
3School of Engineering and Computer Science,Australian National University,Canberra 0200,Australia
Keywords: image encryption,neural mechanism,hyperchaotic system
1. Introduction
Data encryption is an effective method for protecting data.Due to the high correlation between data capacity and the pixels in image information,traditional encryption technology is not suitable for image information. Therefore, protecting image information has become a challenge.[1]
One of the important issues of information security is cryptography,but with the improvement of information security technology,a variety of attack methods have emerged. A traditional cryptography algorithm treats an input plaintext image as a binary stream and does not specifically encrypt the image in a special plaintext form.[2]Plaintext widely exists in people’s daily lives, and images have many unique properties, such as two-dimensional data, uneven energy distribution and a large amount of data. Therefore, in the encryption process, we should fully consider the following characteristics: Firstly,the amount of data in an image is generally large;hence, designing a special algorithm for image security protection to meet the encryption speed requirements of real-time image transmission is very relevant. Secondly,the correlation between adjacent pixels in an image is strong; thus, the correlation should be fully considered in the image encryption process. Thirdly, there are many different types of images;thus,the format of image data cannot be destroyed to prevent abnormal functioning of the image receiver in decoding.
Many people believe that traditional cryptographic algorithms can be cracked; thus, the demand for more advanced security technology is increasing. Therefore, continuing indepth theoretical research and designing more efficient and reliable mathematical models and cryptographic algorithms, in particular, introducing new theoretical methods into the field of information security, are feasible solutions. Now, in addition to algebraic theory, people are trying to introduce the theory and technology of physics, nonlinear science, biology and other disciplines into the field of cryptographic algorithm design. Against this background, chaotic pseudo-random sequence generation algorithms and image encryption technology have been proposed,becoming a popular research topic in the study of encryption technology.
A chaotic system is produced in a deterministic system and exhibits randomness or unpredictability; this is also an essential attribute of nonlinear dynamic systems.[3]Chaotic systems are characterized by their sensitivity to their initial conditions, that is, subtle differences in the initial conditions produce large differences in the results, which further reveal the complexity and uncertainty existing universally in nature and human society. The randomness, immeasurability and sensitivity of a chaotic system to the initial values are naturally related to cryptography. The certainty of a chaotic system ensures consistency in encryption and decryption in the process of secure communication.As long as the property of a chaotic system is applied correctly,a secure encryption system with a high key space can be obtained. The orbital properties of chaotic encryption correspond to the diffusion properties of traditional encryption systems, while the pseudo-random properties and sensitivity of chaotic encryption correspond to the chaotic properties of traditional encryption systems. Since 1997,many new encryption algorithms based on chaotic systems have been proposed,resulting in a new round of research.
An image encryption algorithm based on a chaotic system has strong encryption characteristics because of its large key space, sensitivity and ergodicity to the initial value and control parameters. At present, chaotic image encryption algorithms can be divided into three categories: (1) encryption algorithms based on low-dimensional chaotic systems;(2)encryption algorithms based on high-dimensional chaotic systems;and(3)encryption algorithms based on chaotic systems combined with other methods.
Low-dimensional chaotic systems were the first chaotic systems used in digital image encryption and have simple structures, easy-to-implement hardware and software, and a fast iteration speed. In 1998, Fridrich was the first scholar to use a two-dimensional chaotic system in the process of digital image diffusion and scrambling, which was based on Shannon’s concepts of confusion and diffusion. Since then, many of the scientific research achievements related to image encryption have been realized by using this scrambling diffusion principle. The authors of Ref. [4] proposed an algorithm for rotated medical images that combines a logistic chaotic and tent chaotic system and a DNA coding operation to carry out diffusion operations on scrambled images to obtain ciphertext images, resulting in a good encryption effect. The authors of Ref. [5] proposed an algorithm for scrambling image blocks that involves using zigzag,rotation and random arrangements after the image is divided into blocks and then using logistic chaos to diffuse the scrambled image blocks to obtain ciphertext images. This algorithm is superior to the existing encryption algorithms in medical image encryption. The authors of Ref.[6]proposed a diffusion-scrambling-diffusion structure to encrypt images. Firstly,the image is divided into blocks,and the image blocks are encrypted by using the traditional diffusion method and inverse hybrid cellular automata. Then,two-dimensional logistic chaos is used to encrypt the image blocks. Each image block is diffused and encrypted again,and the final ciphertext image is obtained. This algorithm can resist selective plaintext attacks and offers high security.However,low-dimensional chaotic systems have weaknesses,such as few control parameters,a small key space,short periodicity and limited calculation accuracy, which lead to the existence of certain periodicity in chaotic pseudo-random sequences and affect the solutions of image encryption.
High-dimensional chaotic systems and hyperchaotic systems have been widely used in digital image encryption and have more complex chaotic dynamic characteristics than lowdimensional chaotic systems. They also have more system parameters and a larger key parameter space and can produce better chaotic sequences. The authors of Ref.[7]constructed the S-box of the Galois field and combined Lorenz chaos and the S-box. They used the algorithm to encrypt images and analyzed the security performance. The algorithm has a simple structure and can resist common attacks. The authors of Ref. [8] used a Lorenz chaotic sequence to scramble images and then used a quantum operation to perform diffusion operations on the scrambled image. This algorithm offers strong security and has a good encryption effect on color images.The authors of Ref. [9] combined Lorenz chaos with a Julia set to scramble and encrypt images. This algorithm has a novel and simple encryption structure and offers high robustness and security. The authors of Ref. [10] scrambled images with a two-dimensional hyperchaotic system sequence and then performed a logical XOR operation to obtain the final ciphertext image. The generated chaotic sequence has good randomness,and the encryption algorithm offers high security. It can be seen from the above that the current image encryption algorithms based on high-dimensional chaotic systems and hyperchaotic systems are still designed based on the principles of scrambling and diffusion. However, due to the advantages of high-dimensional chaotic systems, such as more control parameters,a large key space,and better pseudo-randomness,an increasing number of studies still focus on digital image processing and the encryption of high-dimensional chaotic systems and hyperchaotic systems. However, these two types of chaotic systems have some shortcomings and need to be studied further in terms of sequence quantization,randomness and encryption efficiency.
Hybrid digital image encryption algorithms combining chaotic systems with other methods have also been widely studied by scholars,and extensive results have been achieved by incorporating not only the complex chaotic dynamic characteristics of chaotic systems, more system parameters, a larger key parameter space and better pseudo-random sequences,but also various complementary advantages of other methods. The idea of hybrid digital image encryption that combines a chaotic system with other methods is to combine a chaotic system with DNA coding or the wavelet transform to achieve better security performance. The authors of Ref.[11]proposed the use of the discrete wavelet inverse transform combined with two-dimensional sine chaos to fuse and encrypt color images.This algorithm has good feasibility and security.The authors of Ref. [12] compressed images, combined the Kronecker product (KP) with a chaotic system to construct a measurement matrix,and encoded DNA to encrypt the images,which resulted in good robustness and security. The authors of Ref. [13] proposed a three-dimensional memristor circuit system with good nonlinear dynamic performance and used its key stream to encrypt the image, combined with dynamic DNA coding and dynamic diffusion. The algorithm has high encryption efficiency, sensitivity and security and can resist plaintext attacks. The authors of Ref.[14]proposed combining a 2D robust chaotic system with the wavelet transform, a circular index table and partition diffusion to scramble and diffuse an image to obtain the final ciphertext image. This algorithm has high encryption efficiency and security. The authors of Ref.[15]proposed using two-dimensional logistic map and sine map(2D-LSCM),which combines a binary tree and flip to scramble and encrypt image pixels,and then carry out multiplication diffusion operation encryption in the Galois field to obtain the final ciphertext image. This algorithm improves the correlation and security between a key and plaintext. The authors of Ref. [16] proposed scrambling and encrypting an image by using the discrete wavelet transform and Arnold’s cat map and then dividing the scrambled image into blocks before diffusing and encrypting them again. This algorithm has good security. The authors of Ref. [17] proposed a new two-dimensional chaotic system. The chaotic key generated by this system is combined with pixel bit-level scrambling diffusion to encrypt the color image. The algorithm has a large key space and good antiattack ability. The authors of Ref.[18]proposed encrypting an image by combining a fractal sorting vector with a least significant bit(LSB)chaotic system,which offers high security. The authors of Ref.[19]proposed a new image encryption algorithm by combining a logistic chaotic system with transformation and a chaotic substitution box,which is easy to implement and offers high security. The authors of Ref. [20] proposed a four-dimensional hyperchaotic system based on a flux controlled memristor model,which can generate complex chaotic attractors and be applied to an image encryption algorithm with a large key space.
The authors of Ref. [21] proposed a two-dimensional multi-parameter fractional discrete Fourier transform and combined it with the three-dimensional Arnold transform to encrypt color images from the row and column directions. Experiments showed that the algorithm has good resistance to attacks. However, in the process of hybrid digital image encryption, which combines a chaotic system with other methods,there are some shortcomings. For example,in the process of combining these methods,the encryption speed is undoubtedly reduced due to the higher number of steps. Therefore,more in-depth research on this aspect is needed.
Low-dimensional chaotic systems, high-dimensional chaotic systems and hyperchaotic systems all have some disadvantages, such as few control parameters, small key spaces, short periods and limited calculation accuracy,which lead to chaotic pseudo-random sequences with certain periodicity.[22-25]Therefore, to solve these problems, a new four-dimensional hyperchaotic system with a larger key space and better chaotic dynamics performance is proposed in this paper. This system is combined with a cloud model to generate a new sequence,to solve the periodicity problem of chaotic sequences and to be used as a key stream for image encryption.
With the development of artificial intelligence technology, machine learning and deep learning methods have become increasingly and widely used in the field of computer vision. Tasks such as image processing, image recognition,and target detection are also important branches of information science, and there is an inherent close connection between neural networks and cryptography. As highly nonlinear systems, neural networks possess complex phenomena such as chaotic phenomena.[26]A cross-study between neural networks and cryptography should be feasible but must be mutual. Some scholars have focused on how to use cryptography to better protect the security of neural networks, such as the privacy of training data, and many are concerned about how to use neural networks to better achieve cryptographic goals, such as algorithm design, key management, and cryptanalysis. Representative work includes the following: The authors of Ref. [27] designed a new one-way hash function based on a two-layer chaotic neural network. It has outstanding performance in terms of statistics, key sensitivity, and resistance to attacks. Therefore, in related research, this function is widely discussed. The authors of Ref. [28] were the first to use the synchronized nature of neural mutual learning for key agreement and provided important theoretical support and a practical foundation for subsequent research. The authors of Ref. [29] used neural networks for side-channel energy analysis, which can not only identify the mask value but also efficiently recover key information, thereby achieving effective attacks on advanced encryption standard (AES)cryptographic hardware. The authors of Ref.[30]proposed an image encryption algorithm based on the Lorenz chaotic system and perceptron model that shows good key sensitivity and has high robustness to existing attack methods such as unification, cropping, and noise. The authors of Ref. [31] proposed a parallel diffusion encryption algorithm for images that uses chaotic sequences, where the parallel diffusion improves the efficiency and security of the encryption algorithm. The authors of Ref. [32] used a Lorenz chaotic system to generate a chaotic sequence and then generate two fixed semi-tensor scrambling matrices by using the chaotic sequence. Chaotic positioning and sorting are used to scramble, diffuse and encrypt planar images. This system has a novel structure,introduces complex mathematical models into cryptography, and has high security and usability. The authors of Ref.[33]proposed a chaotic image encryption algorithm based on a matrix semi-tensor product (STP) and a composite key. An image is divided into four sub-blocks, which are then scrambled by the Arnold transform. A ciphertext image is obtained by the diffusion operation of the semi-tensor matrix and the mixed linear-nonlinear coupled map lattice(MLNCML)system,and the algorithm is relatively secure. The operation process of a neural network is essentially a nonlinear operation based on neurons,which is used to better utilize the nonlinear characteristics of a neural network,to enhance the scrambling diffusion effect of the encryption algorithm and to improve the security of the algorithm, with the key stream being combined with a neural mechanism. The essence of the neural mechanism is the use of matrix multiplication to calculate the input value and neuron,but the inverse of this kind of operation has difficulty in obtaining the prepared input value. Therefore, the nonlinear characteristics of a neural network are used in this paper,and the use of image pixels as the input value of the neural network and the key stream as the weight value of the neural network is proposed. The logical XOR operation is used to perform diffusion encryption on the image pixels,and this can not only improve the security of the encryption algorithm but also result in an accurately decrypted image.
The block cipher is an important component of cryptography that plays an important role in data security. The development of the block cipher algorithm in 1977 ushered in a new era of block cipher analysis. There are many factors affecting the security of block cipher schemes,such as the block length and key length. Most block ciphers use a Feistel structure,with the advantage being that the encryption and decryption processes are very similar or even identical in some cases,and the code size or circuit implementation of this kind of password is almost halved. The Feistel structure is an iterative cipher,and its internal structure is simple. The value range of elements in the Galois field and its algebraic operation rules give it a certain development space in the field of image encryption. The authors of Ref. [34] used a linear fractional transform function to generate strong S-boxes in the Galois field. The authors of Ref.[35]proposed using the Galois field to encrypt digital images. The authors of Ref. [36] proposed replacing the image block, which, combined with the Galois field, enables the ciphertext image to be obtained. Classical block cipher algorithms are based on modern cryptosystems.However,they can limit the consumption of resources and use a single key stream and round function, resulting in poor diffusion and security. To solve these problems, an improved Feistel structure is proposed in this paper, which divides an image into left and right sub-blocks, uses four key streams,constructs two complex wheel functions,maps them to the Galois field as a whole,and obtains a polynomial randomly in the Galois field. After the iterative scrambling diffusion encryption of image pixels, the final ciphertext image is mapped to the real number field. The encryption structure exhibits high diffusion and is simple. The primitive polynomial is randomly selected in the Galois field. In essence, it is unpredictable,and the corresponding decryption function is also one-time,and thus,one-time encryption communication is realized. The cooperative encryption of multiple key streams solves the security problem after the single key stream is cracked,and the round function is reversible to ensure the correct decryption to improve the overall security and anti-attack of the encryption algorithm.
In summary, most image encryption algorithms based on chaotic systems suffer from the periodicity of chaotic sequences caused by limited accuracy, a highly complex algorithm structure and low security. However, chaotic systems are characterized by good pseudo-random characteristics,unpredictable orbits,and sensitivity to the initial state and control parameters. These characteristics are consistent with many requirements of cryptography. To solve these problems,a new four-dimensional hyperchaotic system with better dynamic performance is proposed in this paper. Combined with the cloud model,a sequence with higher complexity and randomness is generated as the key stream. At the same time,the image is encrypted by combining the neural mechanism,Galois field with improved Feistel structure. Therefore, the security and anti-attack ability of the encryption algorithm are better. Particularly, the new random sequence generated by combining the chaotic system and cloud model is used as the key stream and applied to the subsequent encryption steps,which not only improves the security of the encryption system but also solves the periodicity problem of the chaotic sequence. The nonlinear operation mechanism of neural networks is introduced into the image encryption algorithm,and the diffusion operation is carried out from the row and column directions of the image,which improves the dependence of the key stream and encryption process on the plaintext.Hence,the overall algorithm can effectively resist the chosen-plaintext attack. The essence of combining the improved Feistel encryption structure with the Galois field and randomly selecting the primitive polynomial is that it is unpredictable. The image pixels are scrambled and diffused in the Galois field, which results in one encryption at a time and further improves the overall security of the algorithm. The contributions of this paper are as follows:
1) A new four-dimensional hyperchaotic system is proposed.
2) The new four-dimensional hyperchaotic system and cloud model generate more complex random sequences as the key stream and address the periodicity issues of chaotic systems.
3) A key stream is combined with a neural mechanism,the Galois field and the improved Feistel network to encrypt images in this paper.
4) The experimental simulation results show that the proposed encryption algorithm can reduce the computational complexity, ensure the security of encrypted images in transmission,and thwart attacks during image transmission.
The structure of this paper is as follows. In Section 2, a new hyperchaotic system with a new key stream sequence generator, a neural mechanism and an improved Feistel structure is proposed.In Section 3,a new image encryption algorithm is proposed, and in Section 4, simulation results are given. The security performance analysis of the encryption algorithm is presented in Section 5. Finally,the conclusion of this paper is presented in Section 6.
2. Related work
In this paper, a new four-dimensional hyperchaotic system with a larger key space and chaotic dynamics, a cloud model, a neural mechanism, a Galois field and an improved Feistel network are combined to scramble and spread the image encryption to obtain a better image encryption algorithm with security and anti-attack properties. The related principles and innovations are introduced in the following.
2.1. New four-dimensional hyperchaotic system
Due to the excellent properties of high-dimensional chaotic systems, the following new four-dimensional hyperchaotic system is proposed:
wherea=25,b=0.1,c=40,d=3,e=0.1,andk=8,and the hyperchaotic system(1)is in a chaotic state. When the initial value of system(1)is set to(1,1,1,1),the phase diagram of the system is as depicted in Fig.1.
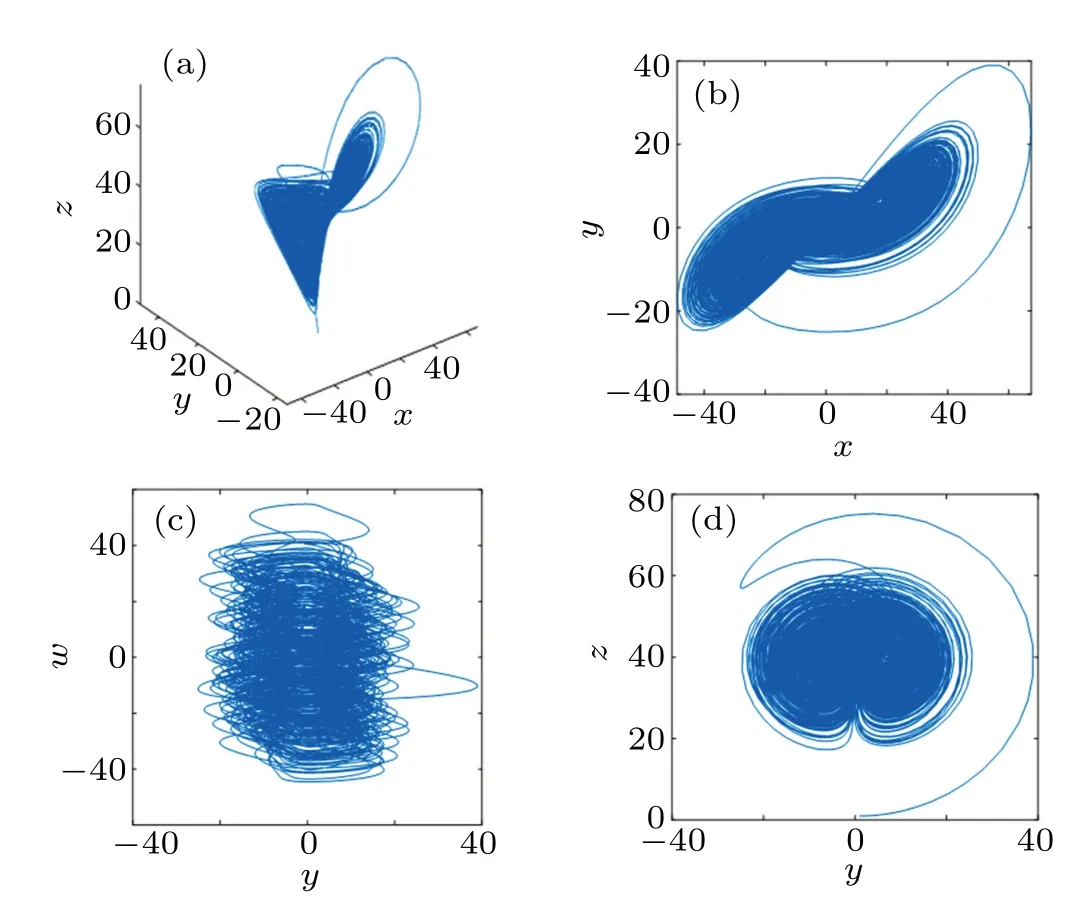
Fig. 1. System (1) phase diagram. (a) x-y-z phase, (b) x-y phase, (c)y-w phase,and(d)y-z phase.
Figure 1 shows that in the range of the phase space, the orbits of the system repel each other,separate,shrink and fold,and fold back and forth countless times, meaning that system(1)is in a hyperchaotic state.
2.2. Analysis of the basic chaotic dynamic behavior
2.2.1. Dissipation
According to dissipative theory, the ΔVvalue of system(1) is less than 0. Thus, system (1) is dissipative and has a chaotic attractor

Letλbe the eigenvalue andIbe the fourth-order identity matrix. By solving the determinant|λI-J|=0,we obtain four eigenvalues,λ1=-65.3360,λ2= 39.2584,λ3=-0.0244 andλ4=-3.According to the judgement condition of Routh-Hurwitz, (0, 0, 0, 0) is an unstable saddle point. Thus, system(1)has chaotic attractors.
2.2.3. Lyapunov exponent
The Lyapunov exponent is an important index for measuring the chaotic state of nonlinear dynamic systems.[37-41]When there is only one positive value in the Lyapunov exponent, a chaotic state is indicated. When there are two or more positive values in the Lyapunov exponents, a hyperchaotic state is indicated. The chaotic control parameters of system (1) area=25,b=0.1,c=40,d=3,e=0.1 andk=8,the number of iterations is 200,and the four Lyapunov exponents of system (1) areLE1=2.3863,LE2=-0.0039,LE3=0.0219 andLE4=-31.5042,which have two positive Lyapunov exponents, showing that system (1) is in a hyperchaotic state. The dimensionDL=3+∑3i=1Li/|L4|=3.0783,and the dimension of the Lyapunov exponent is of fractional order, which indicates that system (1) is in a hyperchaotic state. The Lyapunov exponent spectrum is shown in Fig.2.
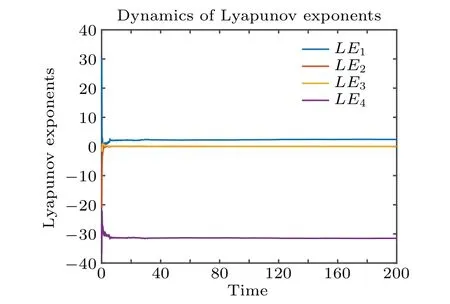
Fig.2. The Lyapunov exponents of system(1).
Figure 2 shows that system(1)has two positive Lyapunov exponents,indicating a hyperchaotic state.
2.2.4. Poincare section
The distribution of points on a Poincare section can be used to verify the chaotic state of a nonlinear dynamic system.If there are a large number of points on the Poincare section,which are flaky and have a fractal structure, the system is in a chaotic state.[42-46]Figure 3 shows the Poincare sections in thex-y,z-w,y-wandy-zplanes.
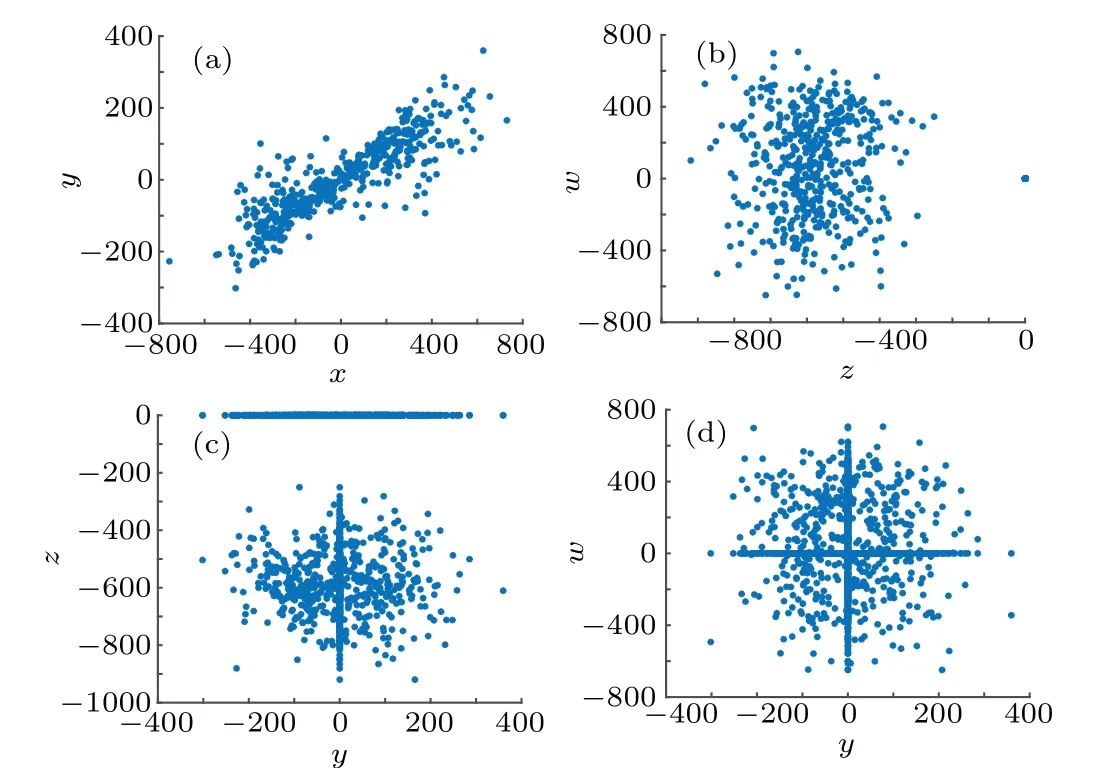
Fig.3. Poincare sections: (a)x-y plane; (b)z-w plane; (c)y-w plane;(c)y-z plane.
Figure 3 shows that a large number of points are in a bifurcated state;hence,system(1)is in a chaotic state.
2.2.5. Bifurcation diagram
The projection of the system on any coordinate axis forms a bifurcation diagram as the parameters change. If there is one point or several points on the bifurcation diagram,the system is in a periodic stable state,and if there are irregular points on the bifurcation diagram, the system is in a chaotic state.[47]The bifurcation diagram of system (1) whenb ∈[0,0.2] is shown in Fig. 4. The two-dimensional Lyapunov exponent spectrum of the four-dimensional hyperchaotic system (1)witha=25,c=40,d=3,e=0.1,b ∈[-0.1,0.3],k ∈[2,8]and the Lyapunov exponent spectrum withb ∈[-0.1,0.3]andk ∈[2,8]are shown in Fig.5.
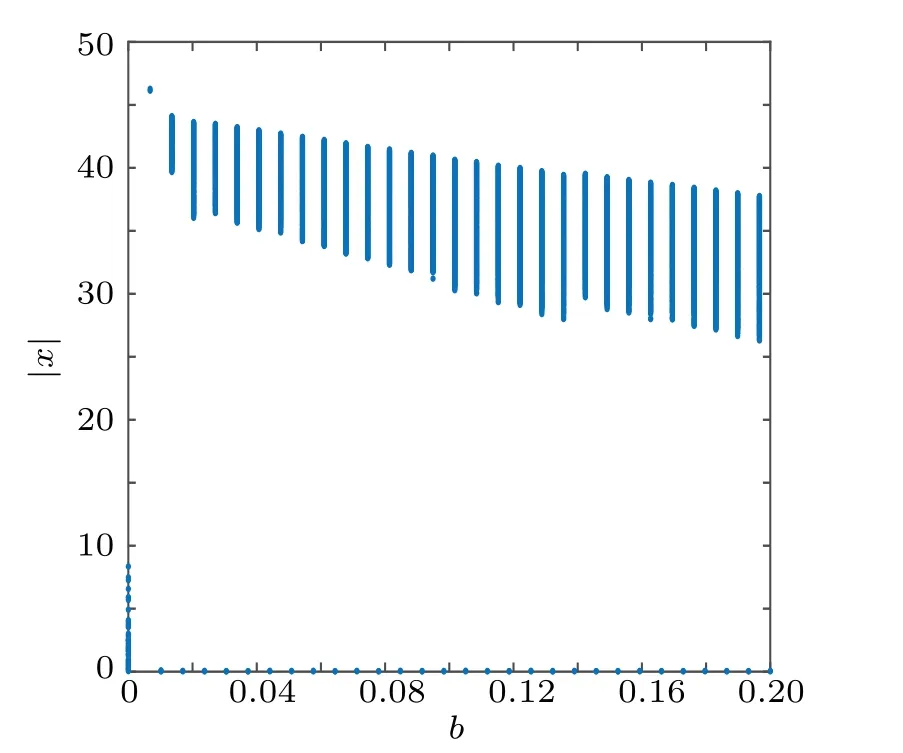
Fig.4. Bifurcation diagram relative to the parameter b.
Figures 4 and 5 show that whena=25,c=40,d=3,e=0.1,b ∈[-0.1,0.3], andk ∈[2,8], the two-dimensional Lyapunov exponent spectrum of system(1)hasLE1=2.2053,LE2=0.0067,LE3=-0.0254 andLE4=-31.3865, which have two positive Lyapunov exponents and the sum of the Lyapunov exponents is-29.1999<0, and shows that system (1) has chaotic characteristics. Whena= 25,c= 40,d=3,e=0.1,k=8 andb ∈[-0.1,0.3],the Lyapunov exponent spectrum of system(1)hasLE1=1.6772,LE2=0.0063,LE3=-0.1525 andLE4=-30.8309, which have two positive Lyapunov exponents, and the sum of the Lyapunov exponents is-29.2999<0. The bifurcation diagram presents a dense distribution state,which indicates that system(1)has chaotic characteristics. Whena=25,b=0.2,c=40,d=3,e=0.1,andk ∈[2,8],the Lyapunov exponent spectrum of system(1)hasLE1=2.2053,LE2=0.0067,LE3=-0.0236 andLE4=-31.3845, which have two positive Lyapunov exponents,and the sum of the Lyapunov exponents is-29.1960<0, and shows that system (1) has chaotic characteristics. The bifurcation diagram presents a dense distribution state,which indicates that system(1)has chaotic characteristics.
2.2.6. NIST test
The test package provided by the National Institute of Standards and Technology(NIST),i.e.,the NIST random test,includes 15 test items that can be used to test the randomness of binary sequences of arbitrary length generated by hardware and software used as secret random or pseudo-random number generators. These testing items are mainly used to determine a variety of types of non-randomness that may exist in a sequence.[49,50]The results of the NIST randomness test are expressed as aP-value. Leta ∈[0.001,0.01] be the significance level interval. WhenP-value>a, the results pass the randomness test;otherwise,they do not pass,which indicates that the chaotic sequence is not random. The four channel chaotic sequences of system (1) are tested by the NIST random test,the results of which are shown in Table 1.
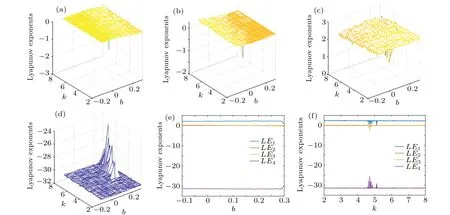
Fig.5. Lyapunov exponent spectrum relative to the parameters b, k. (a)-(d) The two-dimensional Lyapunov exponent spectrum of the fourdimensional hyperchaotic system(1)relative to the parameters b,k. (e)Lyapunov exponent spectrum relative to the parameter b. (f)Lyapunov exponent spectrum relative to the parameter k.
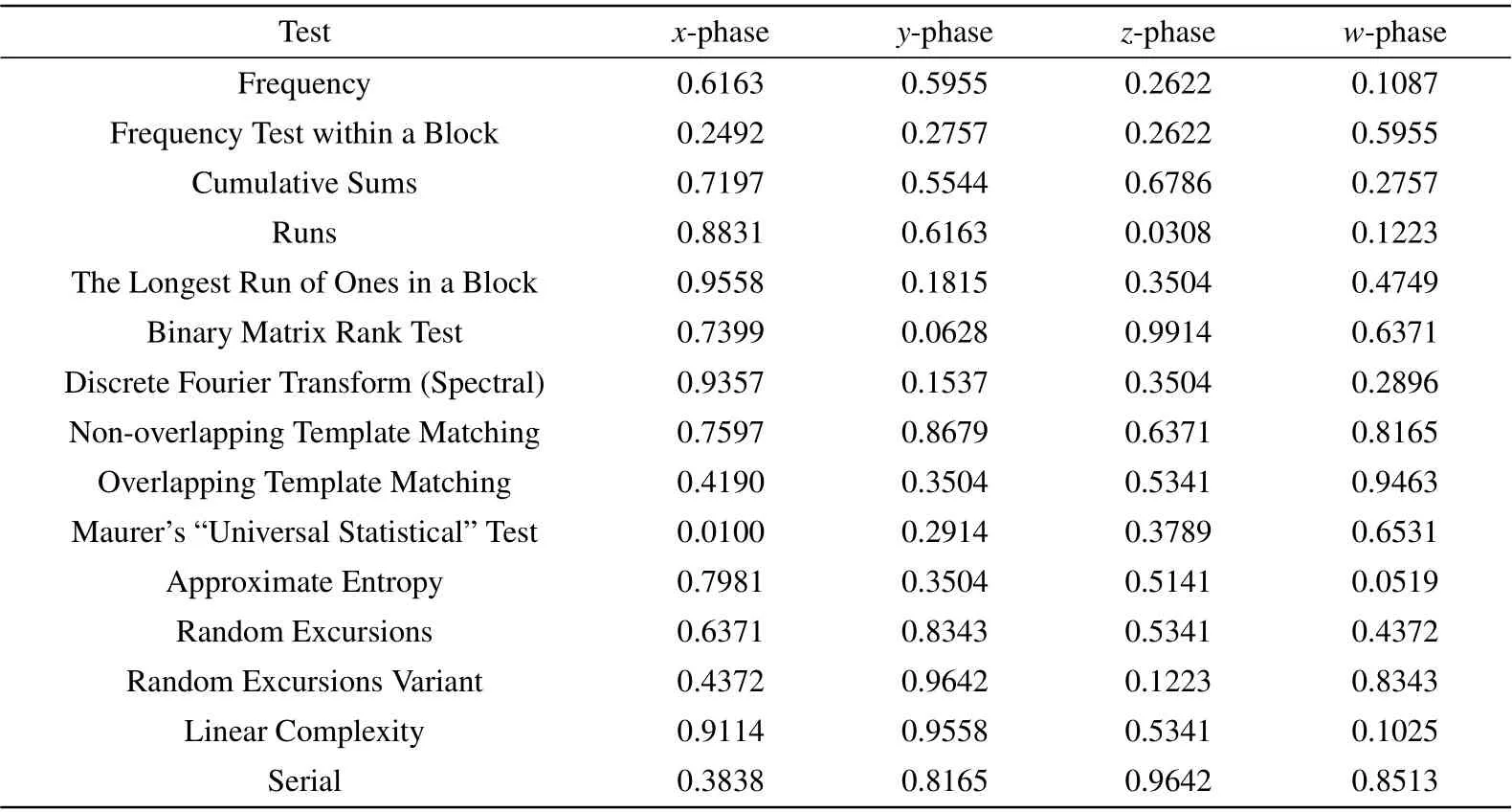
Table 1. NIST test.
Table 1 shows thatP-value>0.001 in all 15 tests, and thus, the chaotic sequence passes the NIST randomness test.Hence, the chaotic sequence of system (1) proposed in this paper can meet the randomness requirements.
2.3. New key stream sequence generator
The cloud model is an uncertain transformation model between a certain qualitative concept and its quantitative expression expressed by a linguistic value[51,52]and has three numerical characteristics, the expected valueEx, entropyEnand superentropyHe.Exis the position of the cloud center of gravity in the cloud droplet group,which is defined as follows:wherexiis the cloud droplet sequence andRNis a normal random number.
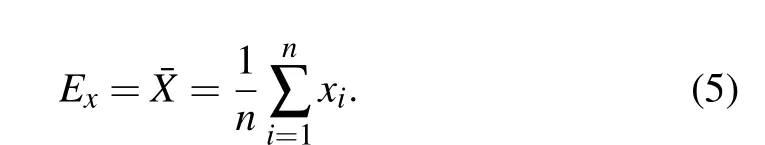

Although the data generated by the cloud model do not have a uniform distribution, the combination of the cloud model and chaotic system can be used to solve the periodic problem of chaotic sequences. Thus, it would have a good encryption effect in encryption applications. Therefore, the cloud model and chaotic sequence are combined to construct a new key stream sequence generator for encryption applications. The structure of the new encryption key stream sequence generator is as follows:

A flow chart of the new key stream sequence generator is shown in Fig.6.

Fig.6. Structure diagram of the new key stream sequence generator.
With the combination of the chaotic sequences of four phases of the hyperchaotic system (1) with the cloud model,the generated new random sequence is analyzed,with the randomness and complexity tested by the approximate entropy,spectral entropy and 0-1 test,as shown in Table 2.
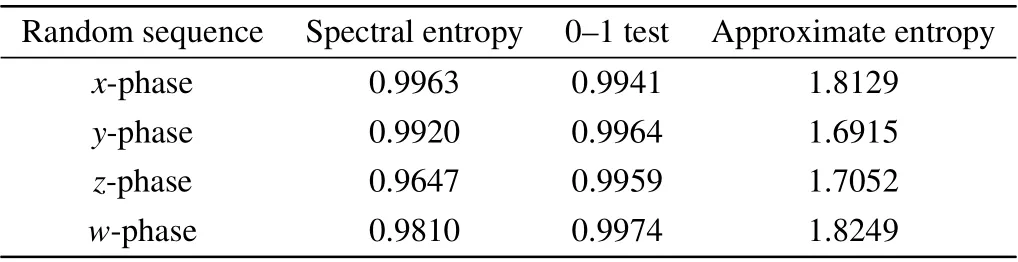
Table 2. The randomness and complexity of random sequences.
Table 2 shows that the new key stream sequence has good randomness and complexity; thus,it is suitable for image encryption.
2.4. Neural mechanism
Artificial neural networks are based on the function of biological neural networks and use mathematical methods to build networks to achieve artificial perception. A neural network structure is considered when building an artificial neural network. At present, approximately 40 kinds of neural network models have been developed.[53,54]According to the structure of the artificial neural network, it can be classified as either a feedforward neural network or a feedback neural network. A feedforward neural network is simple and easy to operate,and a feedforward network with no feedback nodes generally receives a signal from the upper level and propagates it to the next level,as shown in Fig.7.
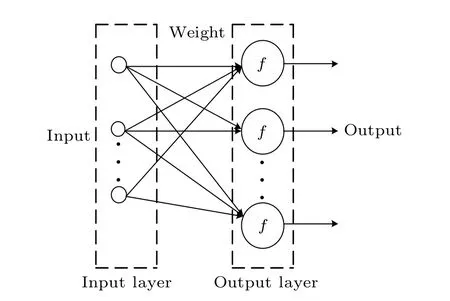
Fig.7. Feedforward network structure diagram.
In Fig.7,weight is the connection between neurons andfis the transfer function of the network and the calculation node of the output-layer neurons. Neural networks are an important branch of information science,and there is a close relationship between neural networks and cryptography. The characteristics of neural networks, such as adaptability, high fault tolerance and associative memory,also meet the requirements of cryptography for key management and attack resistance.However,neural networks are not suitable for image encryption because they use matrix multiplication. The transfer function of a network does not accurately restore the data information in the output to the input.Thus,it cannot be used in an image decryption algorithm.In a neural network,the weight is obtained by training the network, and the operation mechanism of the neural network is essentially based on the principle of the neuron working mechanismy=f(wx+b), wherexis the input data,yis the output data,wis the weight,bis the bias, andf(·)is the activation function,which is introduced into image encryption in this paper. The sequence key stream of arbitrary random length generated by the combined chaotic system and cloud model is used as the weight according to the image size to be encrypted. The weight matrix of corresponding size is then generated. Combined with the working principle of neurons,the image pixels are diffused and encrypted from the row and column directions of the image by matrix multiplication to obtain the ciphertext image.
Assuming that the plaintext image isPand the size isM×N,the plaintext image is used as the input of the feedforward neural network,and the key stream is used as the weight value to diffuse the plaintext image to obtain the ciphertext image. We use the working mechanism of the neural network,and then the plaintext image pixels as the input of the neural network. The key stream is divided into blocks as neurons,and the traditional matrix multiplication is replaced by a logical XOR operator. The calculation process is as follows:

whereC(i,j)is a ciphertext image,keyrow(i,j)is the row key stream,and keycolumn(i,j)is the column key stream.
Through this operation,the security of image encryption is improved, and a new idea is provided for the connection between neural mechanisms and cryptography.
2.5. Improved Feistel structure
Based on the principles of security and the block cipher design, the design of a block cipher structure involves finding an algorithm that can easily and quickly encrypt and diffuse the current input plaintext from a sufficiently good permutation set under the control of a key. The Feistel structure in block cryptography is based on the modern cipher system,which groups the plaintext and then scrambles and diffuses the plaintext information with the round function replacement method combined with the key.The encryption and decryption process appears in pairs. Although it can reduce resource consumption,it adopts a single key stream and round function,resulting in poor diffusion and security.To solve these problems,an improved Feistel structure is proposed. The improved Feistel structure combines the advantages of the original Feistel structure and divides the image into left and right sub-blocks.Primitive polynomials are randomly constructed in the Galois field, and image sub-blocks, the key stream and the wheel function are mapped to the Galois field for scrambling diffusion encryption. After iterative scrambling diffusion encryption of the image pixels,the final image is mapped to the real number field to obtain the final ciphertext image. The encryption structure has high diffusion and a simple structure. The primitive polynomial is randomly selected in the Galois field.In essence,it is unpredictable,and the corresponding decryption function is one-time; thus, one-time encryption communication is realized. The cooperative encryption of multiple key streams solves the security problem after the single key stream is cracked, and the round function is reversible to ensure the correct decryption to improve the overall security and anti-attack ability of the encryption algorithm.
Assuming that the plaintext image isPand the size isM×N, the image is divided into left sub-blockLand right sub-blockR. The key stream sequences are key1, key2, key3 and key4. The single-round encryption process is as follows:
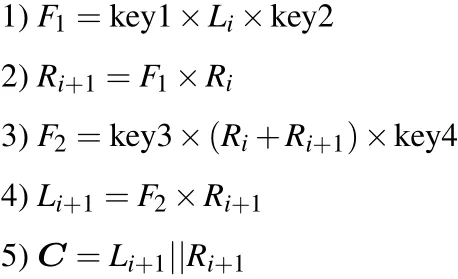
whereLiandRiis the sub-block before encryption,Li+1andRi+1is the sub-block after encryption,||is the connection symbol,andCis the ciphertext image.
The encryption structure is shown in Fig.8.
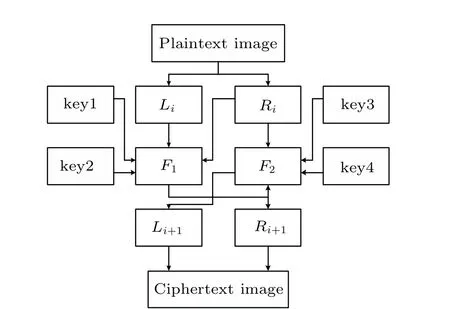
Fig.8. Encryption flow chart of the improved Feistel structure.
Decryption is the reverse process of encryption. Assuming that the ciphertext image isCand the size isM×N, the ciphertext image is divided into left sub-blockLand right subblockR. The key stream sequences are key1,key2, key3 and key4. The single-round decryption process is as follows:

whereLi+1andRi+1is the sub-block before decryption,LiandRiis the sub-block after decryption,||is the connection symbol,andPis the decryption image.
The decryption process is shown in Fig.9.
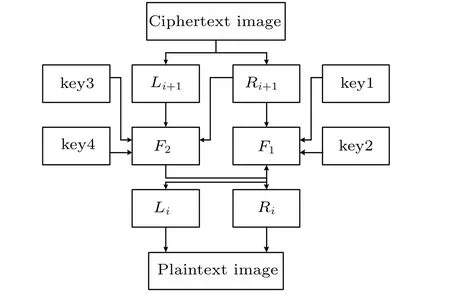
Fig.9. Decryption flow chart of the improved Feistel structure.
2.6. Galois field operation
The order of the Galois field(finite field)GF(Pn)must be a prime powerPn,wherenis a positive integer. For example,GF(28)is a finite field composed of 28elements,and all elements are integers from 0 to 28-1. All elements inGF(28)can be uniquely represented by an 8-bit sequence. Any polynomialf(x)onGF(28)is
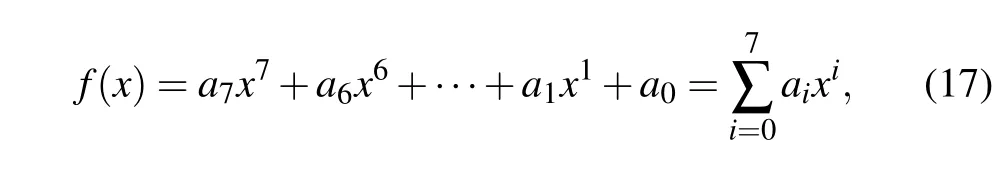
whereai ∈{0,1},i=0,1,2,...,7. Therefore, the elements onGF(28)and the polynomials onGF(28)have a one-to-one correspondence. According to the given primitive polynomials onGF(28),by using mathematical operations such as addition, subtraction, multiplication and division in the Galois field,the element value range of the new matrix obtained after the mathematical operations ofGF(28)is still[0,28-1]. The multiplication operation onGF(28)breaks through the limitation of the numerical operation in previous digital image encryption algorithms. This breakthrough not only accords with the value characteristics of the grey value of grey image pixels but also enriches the diffusion operation of the encryption algorithm. Therefore,the encryption and decryption process of the improved Feistel network is moved to the Galois field in this paper. The overall security of the encryption algorithm is thus improved.
3. Encryption and decryption algorithm
The encryption algorithm proposed in this paper includes three main stages. Firstly, through the new four-dimensional supermodel, the chaotic system is combined with the cloud model,and the generated sequence is used as the key stream.The sequence not only has good randomness and complexity but also solves the periodicity problem of the chaos.Secondly,using a neural mechanism,the plaintext image pixels are used as the input data of the neural network, and the key stream sequence is divided into blocks as the weight. Then,the neural network logic XOR diffusion operation is carried out to obtain the middle ciphertext image. Finally,to improve the security of the algorithm,the improved Feistel structure is used to scramble the middle ciphertext image in the Galois field and to obtain the final ciphertext image. The encryption and decryption process is shown in Fig.10.
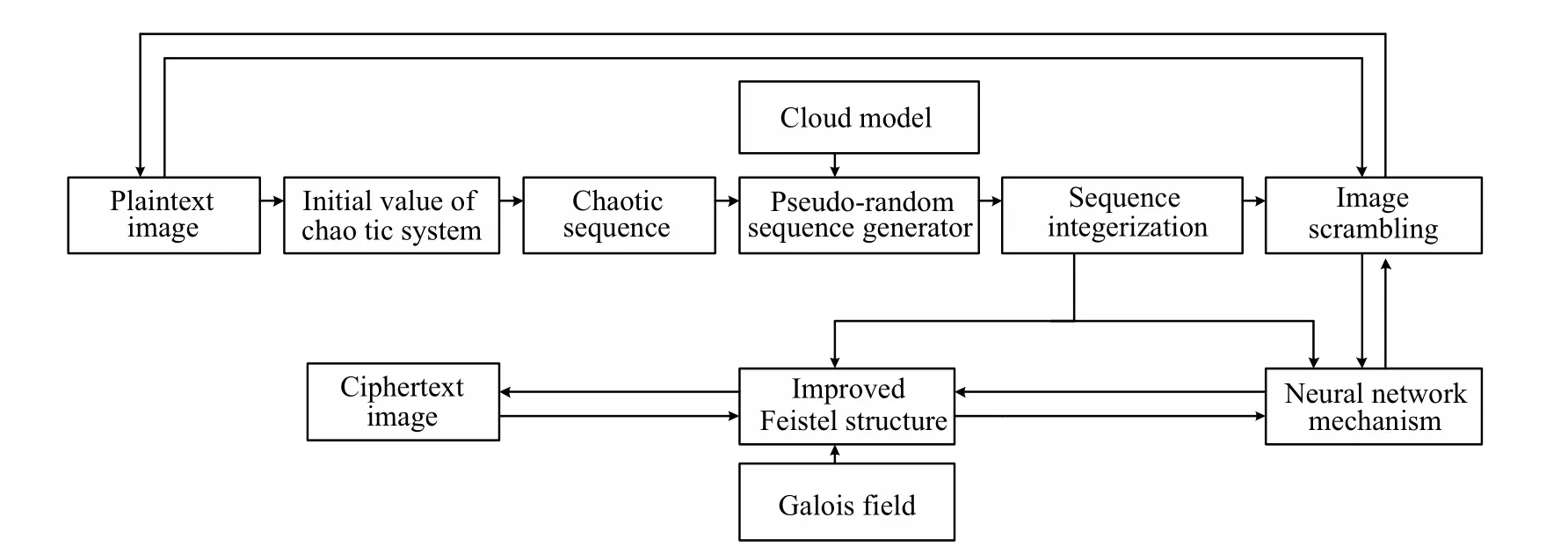
Fig.10. Encryption and decryption flow chart.
3.1. Image encryption algorithm
Assuming that the plaintext image isPand the size isM×N,the specific encryption steps are as follows.
3.1.1. Key stream generation
Step 1 Calculate the initial values init1, init2, init3and init4of the hyperchaotic system(1).The process is as follows:
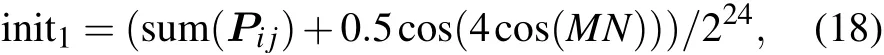

where sum(·)is the sum operation and mod(·)is the modular operation.
Step 2 The initial values init1, init2, init3and init4are brought into system (1) and combined with the cloud

wherek=1,2,...,256,i=1,2,...,256,bitxor(·)is the XOR operation,and mod(·)is the modular operation.
3.1.3. Generation of the final ciphertext image
The Feistel packet structure is simple and offers high encryption efficiency. Additionally,the Galois field can map image pixels according to different primitive polynomials,which

whereGF(·) is the multiplication in the Galois field,F1andF2are round functions andi=1,2,...,M×(N/2).
3.2. Image decryption algorithm
The image encryption algorithm designed in this paper uses a symmetric encryption structure. Therefore, the corresponding decryption algorithm is the reverse process of the encryption algorithm.The detailed decryption steps are as follows.
Step 1 The received key is taken as the initial value of the hyperchaotic system(1),and the key stream in the decryption process is generated iteratively with the cloud model.
Step 2 The ciphertext image is decrypted by using the key stream combined with the improved Feistel decryption structure and Galois field,and image matrixP1is obtained.
Step 3 Image matrixP1is used as the input of the neural network,the key stream is output,and the XOR operation is still applied. The function is activated to take the modulus operation to obtain image matrixP2.
Step 4 Image matrixP2is combined with the key stream for the scrambling inverse operation, and the final decrypted image matrixP3is obtained.
4. Experimental results
We select a size of 256×256 for the plaintext image experiment, and the initial value is generated by a plaintext image calculation. The plaintext images, encryption and decryption results obtained on a Windows 7 platform with 4 GB of memory and a MATLAB 2018b simulation are shown in Fig.11.
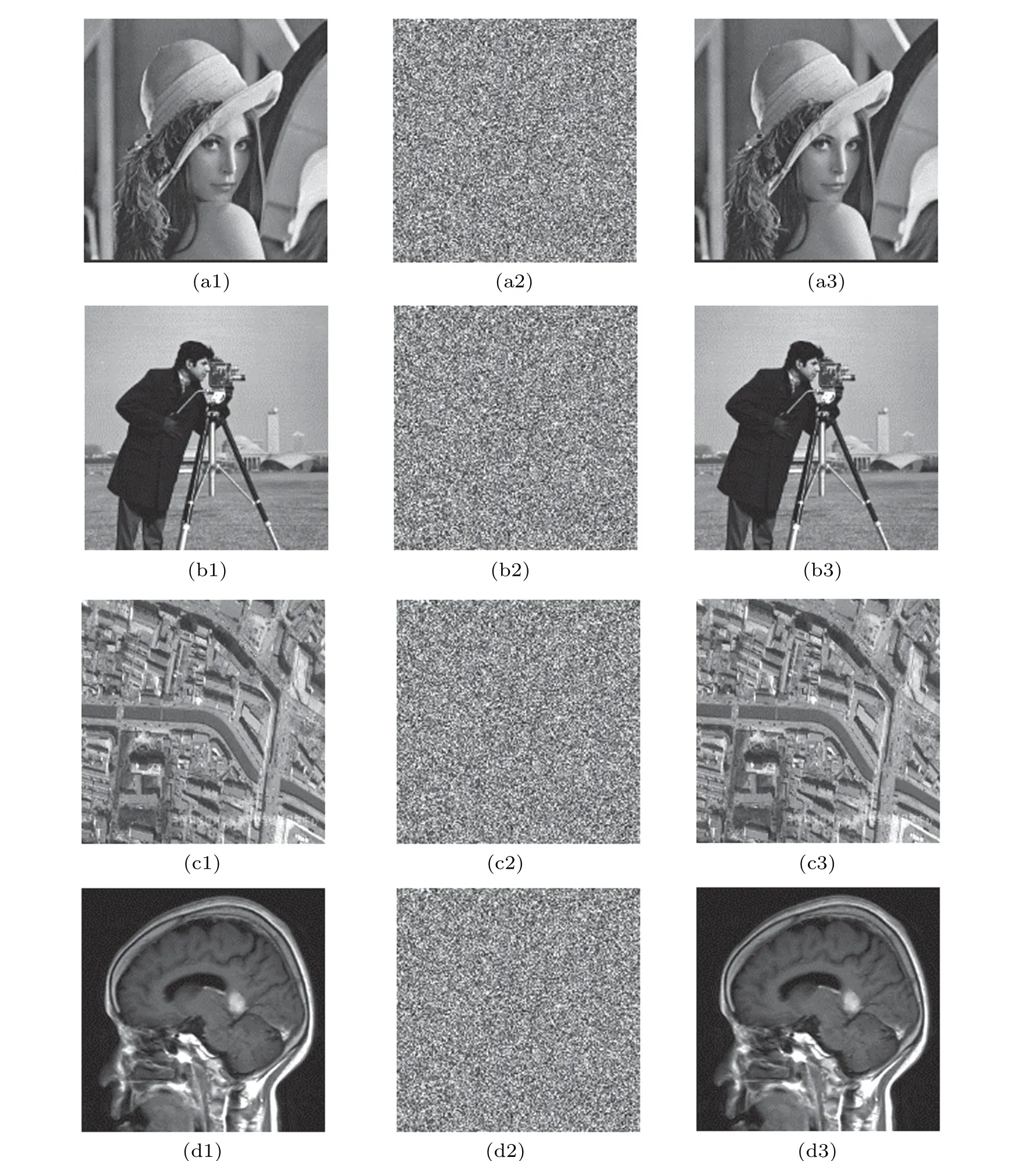
Fig.11. Encryption and decryption results. (a1)is the Lena plaintext image,(a2)is the Lena ciphertext image,(a3)is the Lena decrypt image,(b1) is the cameraman plaintext image histogram, (b2) is the cameraman ciphertext image, (b3) is the cameraman decrypt image, (c1) is the remote-sensing plaintext image,(c2)is the remote-sensing ciphertext image,(c3)is the remote-sensing decrypt image,(d1)is the CT plaintext image,(d2)is the CT ciphertext image,and(d3)is the CT decrypt image.
5. Safety analysis
5.1. Histogram analysis
A histogram reflects the distribution of image pixel values. If the histogram distribution is not uniform, attackers can obtain information from it. Thus, the plaintext image histogram should be evenly distributed to resist statistical attacks.[55-57]Figure 12 shows the histograms of Lena plaintext images and ciphertext images.
Figure 12 shows that the histogram distribution of the ciphertext image is uniform, completely different from that of the plaintext image. In addition, the histogram variance can be used to measure the uniformity of a histogram.[58,59]The definition is as follows:
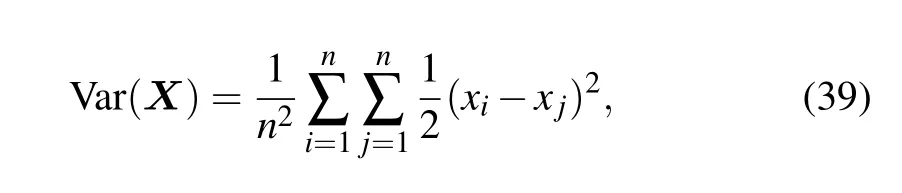
whereX={x0,x1,...,x255}is the value vector of the histogram,xiandxjare the number of grey values ofiandj,respectively, andnis the grey level. The variance results of the ciphertext images are listed in Table 3.
Table 3 shows that the histogram variance of the proposed method is large and that all algorithms meet the requirement of a standard value greater than 293.2478.
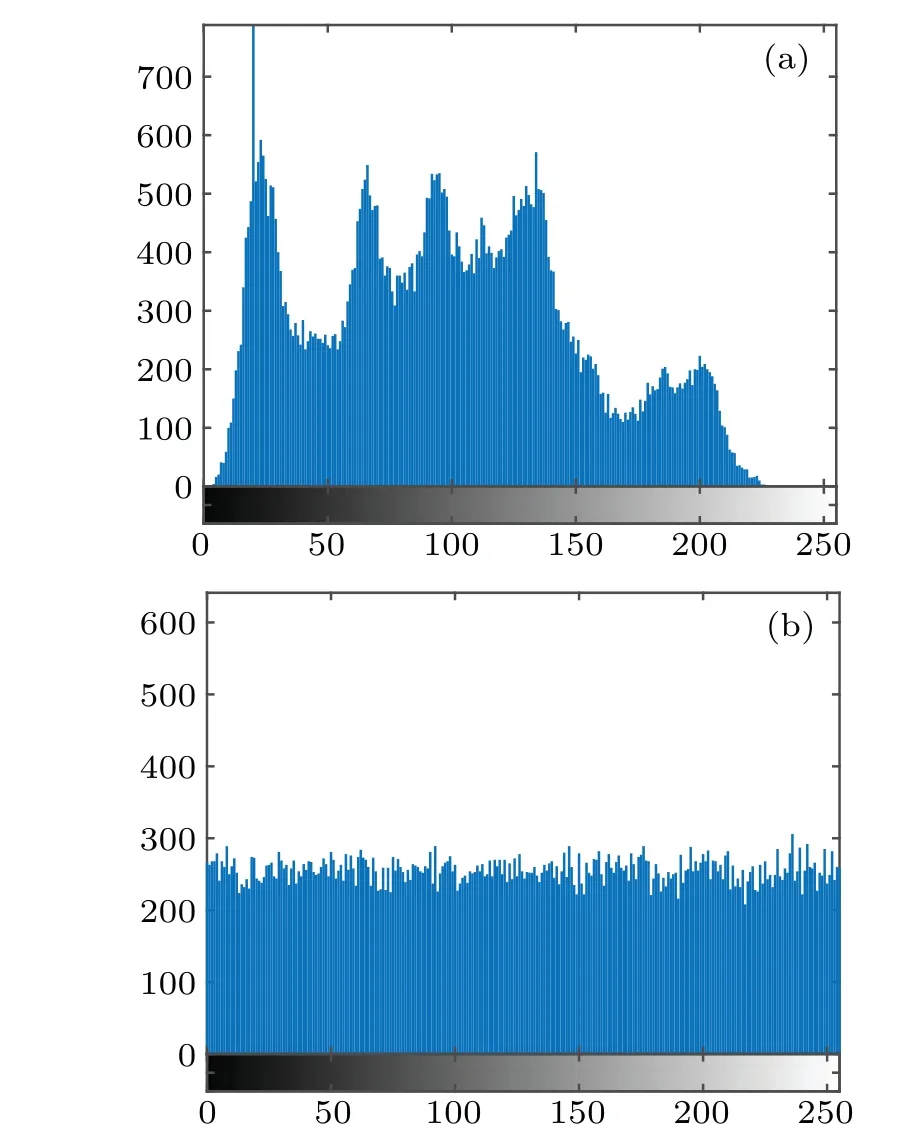
Fig. 12. Histograms of a plaintext image and a ciphertext image. (a)is the Lena plaintext image histogram, and (b) is the Lena ciphertext image histogram.

Table 3. Histogram variance.
5.2. Information entropy analysis
Information entropy measures the randomness of information.[63,64]The information entropyH(m)of message sourcemis defined as
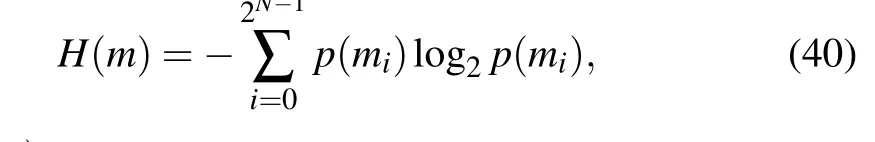
wherep(mi)is the probability ofmiandNis the digit capacity ofmi. The closer the ciphertext entropy of the grey image is to 8, the more chaotic the image is. Table 4 lists the information entropy of the test image and ciphertext image and the results of a comparison with other schemes. The information entropy of the ciphertext image obtained by the proposed encryption algorithm is consistent with those in Refs.[60-62]and slightly higher than those of the other two encryption algorithms; thus, the ciphertext image encrypted by the proposed encryption algorithm has good randomness.
Table 4 shows that the information entropy of the ciphertext image in this paper is higher than that of the related literature;thus,the ciphertext encrypted by the proposed algorithm has good randomness.
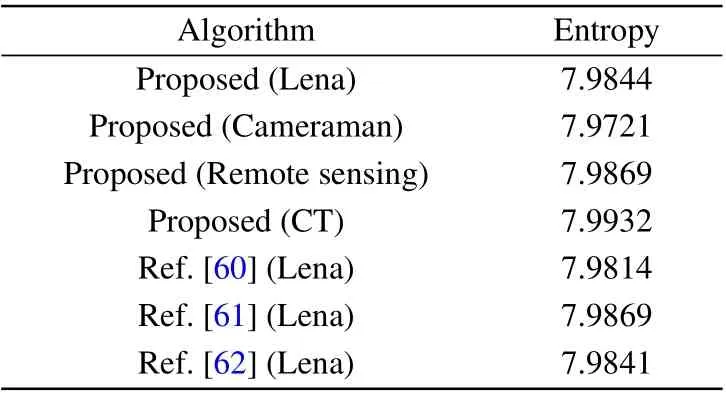
Table 4. Information entropy.
5.3. Key space analysis
When the key space of an encryption system is larger and the key is more complex,the ability of the system to resist exhaustive attacks will be stronger. The encryption space is analyzed from the perspective of cryptography. If the key space of the algorithm is greater than 2100≈1030,it can be said that the minimum security requirements have been met.[63-68]In the encryption process proposed in this paper,the parametersa,b,c,d,e,kand initial valuesx,y,z,wof the new fourdimensional hyperchaotic system can be used as keys for encryption. Generally, on a 64-bit computer operating system,the precision of the floating-point number is approximately 10-15. Therefore, the key space in this chapter is approximately (1015)10=10150, which shows that the key space is larger than the security level; thus,it can resist exhaustive attacks.
5.4. Key sensitivity analysis
The ideal cryptosystem should be highly sensitive to the key,and any slight change to the key will lead to an incorrect decryption image.[69,70]Figure 13(a) is the Lena image after decryption with the correct key,and Figs.13(b)-13(d)are the decrypted images after adding 10-14to the keysa,bandc,respectively.

Fig.13.Key sensitivity analysis:(a)decrypted image of the correct key;(b)decrypted image of a+10-14;(c)decrypted image of b+10-14;and(d)decrypted image of c+10-14.
Figure 13 shows that any slight change to the key leads to an incorrect decryption image; hence,the algorithm is highly sensitive to the key.
5.5. Correlation analysis
The strong correlation between adjacent pixels in plaintext images is an inherent attribute of images.[71]To test the correlation of the ciphertext image generated by the proposed encryption algorithm,we randomly select 5000 pairs of adjacent pixels from multiple ciphertext images and calculate the correlation coefficient between the adjacent pixels through the following equation:
where
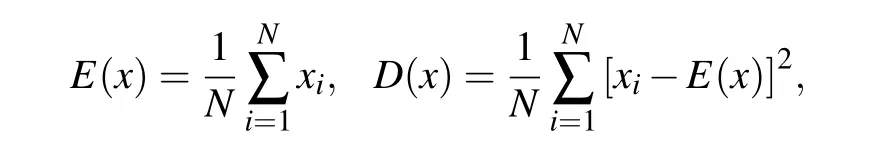
x,yindicate the location of the adjacent pixel, andNis the total number of pixels. Figure 14 shows the correlation distribution of the Lena plaintext image and the corresponding ciphertext image in the horizontal,vertical and diagonal directions. There is a strong correlation between adjacent pixels in the Lena plaintext image,and the correlation between adjacent pixels of the ciphertext image is very low. Table 5 shows a comparison of the results of the correlation coefficients with those of other encryption algorithms.
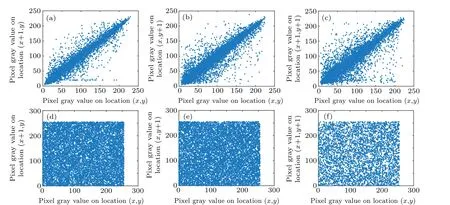
Fig. 14. Correlations between adjacent pixels. (a) Horizontal correlations for the Lena plain image. (b) Vertical correlations for the Lena ciphertext image. (c) Diagonal correlation for the Lena plain image. (d) Horizontal correlation for the Lena ciphertext image. (e) Vertical correlation for the Lena plain image. (f)Diagonal correlation for the Lena ciphertext image.
Table 5 shows a comparison with the ciphertext images produced in Refs. [60-62]. Clearly, the correlation between adjacent pixels in the ciphertext images produced by the proposed encryption algorithm is very low.

Table 5. The resulting correlation coefficients.
5.6. Differential attack analysis
The key sensitivity reflects the key sensitivity of the decryption algorithm. In this section, the change rate of the number of pixels (NPCR) and the unified average changing intensity(UACI)are used to quantitatively analyze the differences between plaintext images and decrypted images.[72]The NPCR and UACI can be expressed by
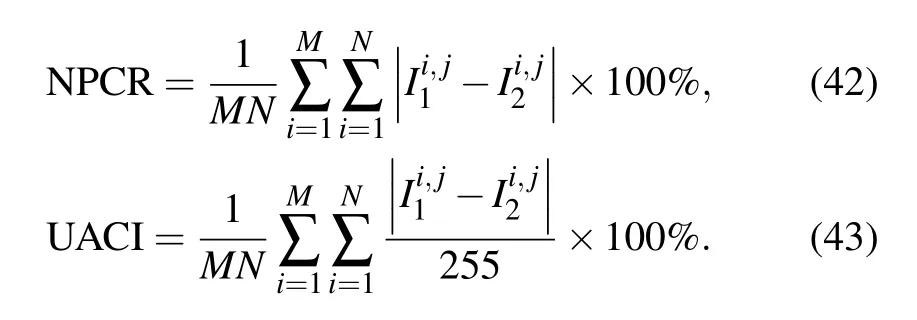
Ideally, the expected NPCR and UACI values would be 99.6094% and 33.4635%. We randomly select 1000 pixels at different positions and change the lowest position of each pixel. Then, we compare the new ciphertext image with the original ciphertext image and calculate the average values of the NPCR and UACI.The test results and results of a comparison with other methods are shown in Tables 6 and 7.
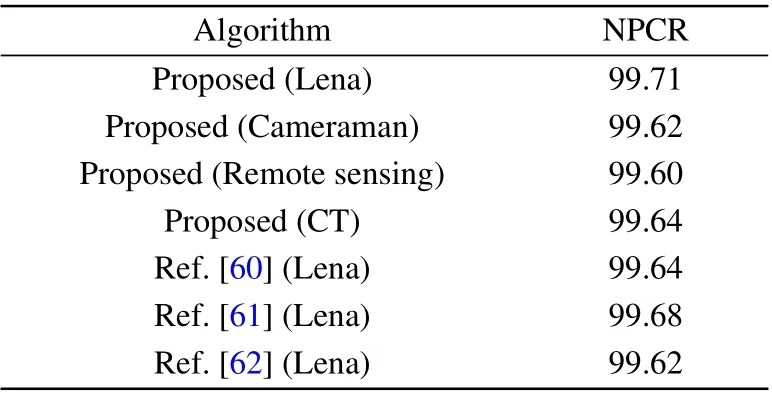
Table 6. NPCR(100%).
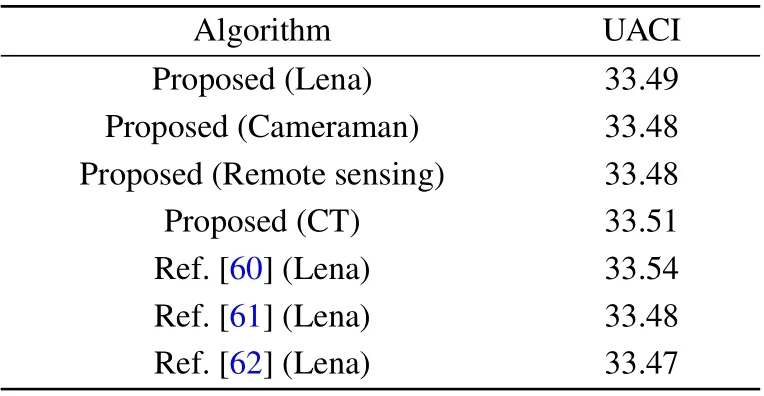
Table 7. UACI(100%).
Tables 6 and 7 show that the NPCR and UACI of the ciphertext image of the proposed algorithm are very close to the theoretical values of 99.6094% and 33.4635%, respectively,meaning that the proposed algorithm can effectively resist differential attacks.
5.7. Time-complexity analysis
In practical applications, in addition to the evaluation of the security of the encryption algorithm, the performance of the encryption algorithm is evaluated; for this purpose, the time complexity is used. The time complexity of the proposed encryption algorithm includes the following three main stages:the key generation stage,the key stream generation stage and the encryption stage. Generally,the complexity of image preprocessing is negligible. The total time complexity of the proposed encryption algorithm isO(2MN). In addition, a highdimensional chaotic system has a complex structure,requires a large number of computations and has a high physical cost.Therefore, when encrypting large-scale plaintext images, the first step is to generate the key stream and then to encrypt each image block in parallel to improve the efficiency of the algorithm.
6. Conclusions
A new image encryption method is proposed in this paper that offers high security and is based on a new fourdimensional hyperchaotic system, a cloud model, a neural mechanism, an improved Feistel network and a Galois field.The encryption algorithm includes three main stages. Firstly,a new four-dimensional hyperchaotic system is constructed and combined with a cloud model to generate a sequence as a key stream. The sequence has a large key space and solves the problem of chaotic system periodicity. Secondly, the key stream is combined with a neural mechanism, an improved Feistel network and a Galois field to encrypt the image by pixel scrambling and diffusion. Finally, the security of the ciphertext image is analysed to prove the security of the proposed image encryption algorithm.The algorithm has a simple structure and high security and can meet the needs of practical encryption applications.
Acknowledgements
We thank all the teachers in the research group. Project supported by the National Natural Science Foundation of China (Grant No. 61973248) and the Key Project of the Shaanxi Key Research and Development Program, China(Grant No.2018ZDXM-GY-089).
- Chinese Physics B的其它文章
- Quantum walk search algorithm for multi-objective searching with iteration auto-controlling on hypercube
- Protecting geometric quantum discord via partially collapsing measurements of two qubits in multiple bosonic reservoirs
- Manipulating vortices in F =2 Bose-Einstein condensates through magnetic field and spin-orbit coupling
- Beating standard quantum limit via two-axis magnetic susceptibility measurement
- Anti-function solution of uniaxial anisotropic Stoner-Wohlfarth model
- Ratchet transport of self-propelled chimeras in an asymmetric periodic structure

