Juewen Fan(范玨雯) Bingyan Jiang(江丙炎) Jiaji Zhao(趙嘉佶) Ran Bi(畢然) Jiadong Zhou(周家東)Zheng Liu(劉政) Guang Yang(楊光) Jie Shen(沈潔) Fanming Qu(屈凡明) Li Lu(呂力)Ning Kang(康寧) and Xiaosong Wu(吳孝松)

1State Key Laboratory for Artificial Microstructure and Mesoscopic Physics,Frontiers Science Center for Nano-optoelectronics,Peking University,Beijing 100871,China

2Key Laboratory of Advanced Optoelectronic Quantum Architecture and Measurement(Ministry of Education),Beijing Key Laboratory of Nanophotonics&Ultrafine Optoelectronic Systems,and School of Physics,Beijing Institute of Technology,Beijing 100081,China

3School of Materials Science and Engineering,Nanyang Technological University,Singapore 639798,Singapore

4Beijing National Laboratory for Condensed Matter Physics,Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China

5Key Laboratory for the Physics and Chemistry of Nanodevices and Department of Electronics,Peking University,Beijing 100871,China

6Collaborative Innovation Center of Quantum Matter,Beijing 100871,China

7Shenzhen Institute for Quantum Science and Engineering,Southern University of Science and Technology,Shenzhen 518055,China

Keywords: Fraunhofer pattern,Josephson junction,spin–orbit coupling,homointerface

In the past decade, the interplay between spin–orbit coupling (SOC) and superconductivity through the proximity effect has received significant attention.[1–5]In materials with strong SOC, a variety of interesting effects may occur when combining them with superconductors, depending on the form of the SOC, structural symmetry, etc.[1,4,6–10]For instance, transition metal dichalcogenides with an Ising SOC can turn a conventional s-wave superconductor into an Ising superconductor through the proximity effect.[5]Another example, which has attracted enormous interest, is the construction of the Majorana zero mode in spin–orbit coupled nanowires or topological insulators in close proximity to swave superconductors.[3,11–15]In Josephson junctions (JJs),the combination of a Zeeman field and a Rashba spin–orbit interaction can give rise to a supercurrent, even if the phase difference between the two superconductors is zero,realizing aφ0junction.[1,2,4]

A major playground for such studies is superconductor–normal metal–superconductor(SNS)JJs,in which the normal metal provides SOC.It is well-known that the critical current of a conventional JJ as a function of magnetic field exhibits a Fraunhofer interference pattern,described by[16]

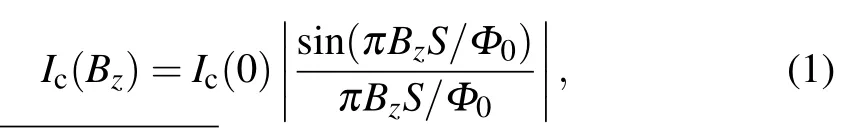
whereIcis the critical current,Bzthe magnetic field perpendicular to the junction plane,Sthe effective area of the junction,andΦ0=h/2eis the flux quantum.Icis apparently independent of the polarity ofBz,I±c(Bz)=I±c(-Bz), where±indicates the current polarity. Its amplitude usually remains unchanged upon reversing the currentI,too,I+c(Bz)=-I-c(Bz).That is,the Fraunhofer pattern is symmetric inBzandI. However, recent studies have shown that these symmetries can be broken, especially in the presence of SOC. Broken current symmetry may be induced by structural asymmetry of the junction,[17–19]or a multi-band effect.[2,7,20]Broken field symmetry was attributed to disorder potentials,[21]or nonuniform SOC.[22–24]Most of these cases require extrinsic mechanisms,which often exist in a practical junction. A general relation between the pattern asymmetry and the combination of a spin–orbit coupling, in-plane magnetic field and disorder has been theoretically studied.[6,10]

Here we study JJs fabricated with a novel material,V5S8of a heterodimensional superlattice, whose special form of SOC gives rise to a rare in-plane Hall effect.[25]The homointerface of the junction enables investigation of intrinsic effects.It is found that both the magnetic field and current symmetries of the Fraunhofer pattern are broken. Moreover, the pattern can be tuned by an in-plane field. Consistent patterns and field dependence are observed in all devices.The phenomenon suggests a nontrivial spatial distribution of the Josephson current that is intrinsic to V5S8and stems from its SOC.

Micro strips of V5S8films were grown by chemical vapor deposition on SiO2substrates.[25]Strips with about 10 nm thickness were selected for this study. As for superconductors, 31 nm aluminum, following a 2 nm titanium adhesion layer,were e-beam deposited. Some measurements were performed in an Oxford3He cryostat with a base temperature of 250 mK.Experiments at a lower temperature were carried out in an Oxford dilution refrigerator with a base temperature of 10 mK.The magnetic field was provided by a three-axis vector superconducting magnet. To avoid the effect of hysteresis due to heating during a bias current sweep,the sweep always started from zero.

V5S8film used in this study has a unique superlattice structure, in sharp contrast with the conventional V5S8compounds.[25]It can be seen as VS2layers intercalated with V2S2atomic chains. It exhibits an extraordinary inplane Hall effect, suggesting a peculiar form of spin–orbitcoupling. Because Al(31 nm)/V5S8(10 nm)bilayers are nonsuperconducting due to a strong inverse proximity effect,aluminum JJs can be made using the Al(31 nm)/V5S8(10 nm)bilayer as the normal metal weak link.[26]The JJ is a crossbar structure made from a V5S8strip and an aluminum strip.The resultant homointerface between the superconductor and normal metal is highly transparent and uniform,providing an ideal JJ platform for investigation of the intrinsic effect of SOC.

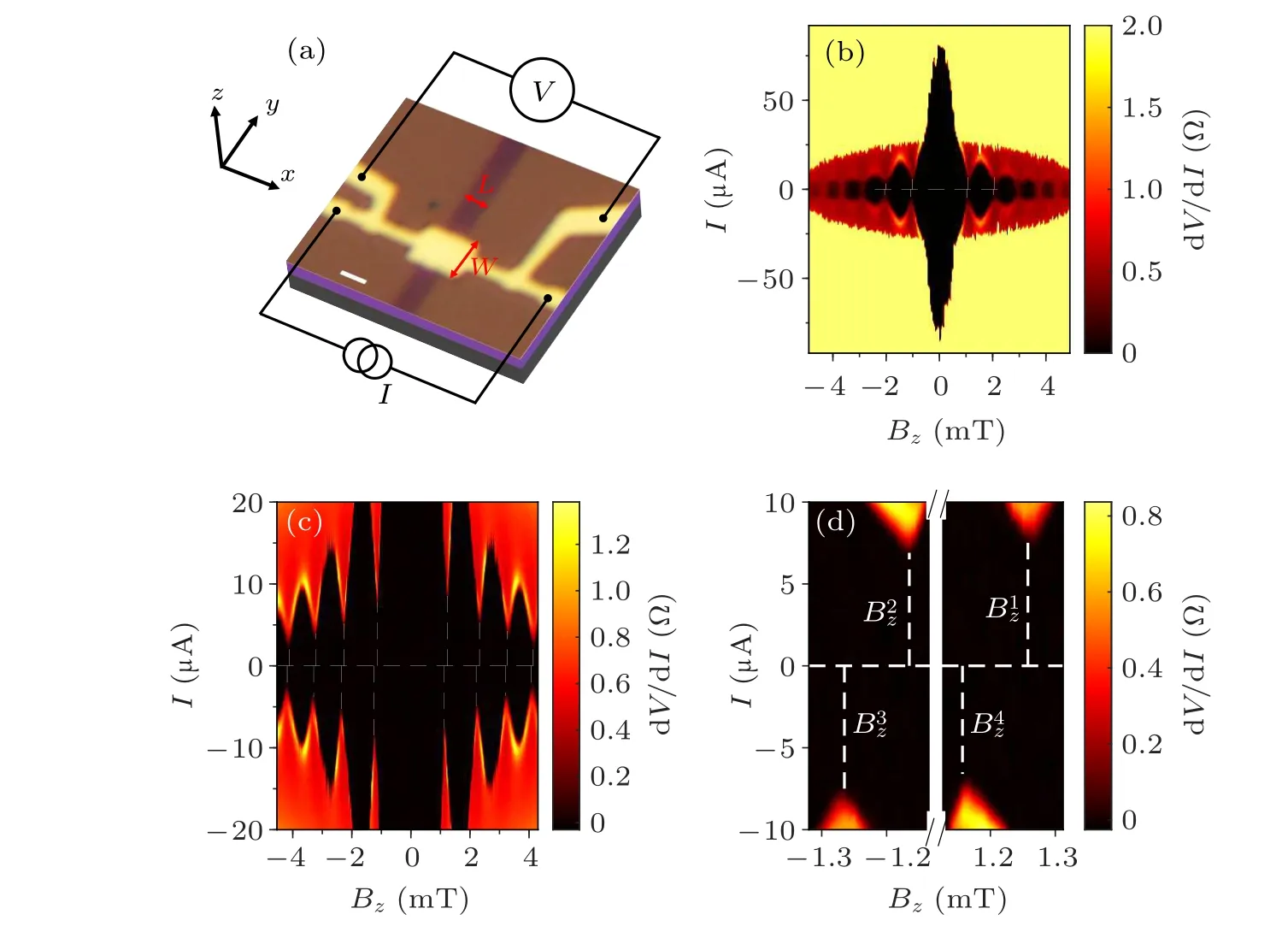
Fig.1. Fraunhofer interference patterns of a JJ.(a)An optical micrograph of the device with an illustration of the measurement configuration. The junction length is L=0.92 μm, the junction width is W =1.75 μm. The scale bar is 1 μm. (b)The interference pattern at 250 mK.The dashed white lines indicate the position of the nodal points and I =0. (c) The zoom-up pattern taken at 32 mK. (d) The further zoom-up scan on the first-order nodes in(c). A break in the x axis is introduced for better comparison.

In another word, the diffraction pattern is inversion symmetric if the total magnetic field is considered. This can also be directly seen in Fig.2,where the pattern atθis inversion symmetric to that atθ+180°.

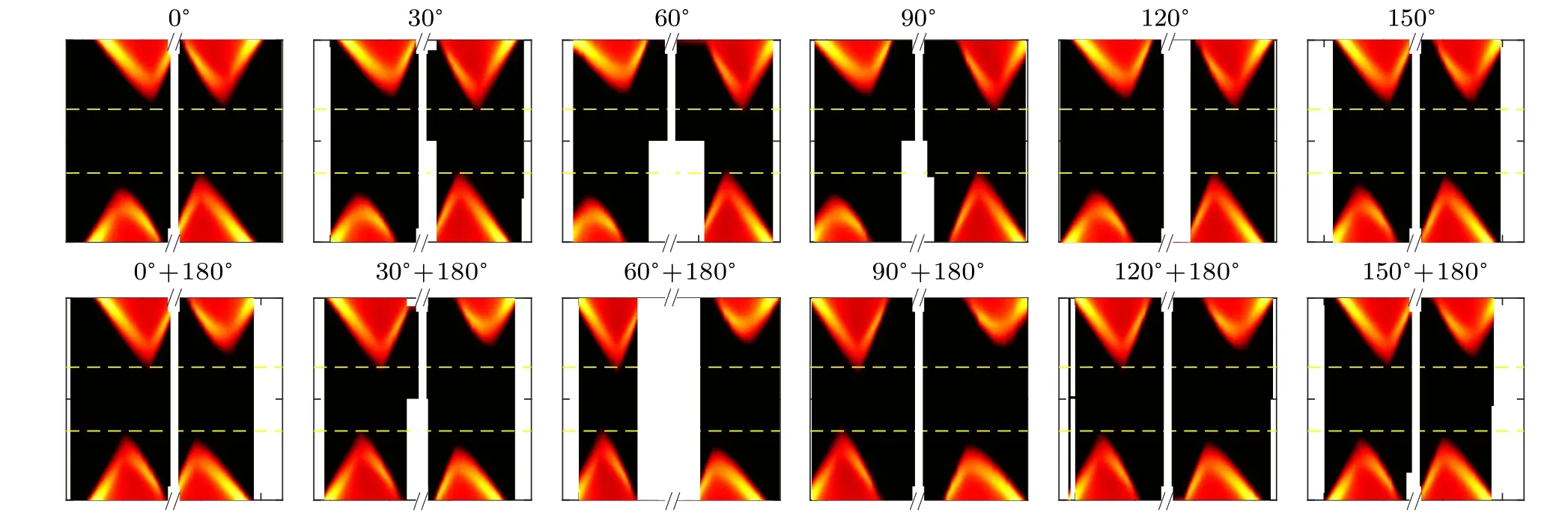
Fig.2. Fine mapping of the first-order nodes in the interference pattern in the presence of B‖ =0.12 T oriented at different angles with respect to the x axis. Two dashed yellow lines at I=±3.158 μA are used as a baseline to highlight the shift of the critical current at the nodal points.

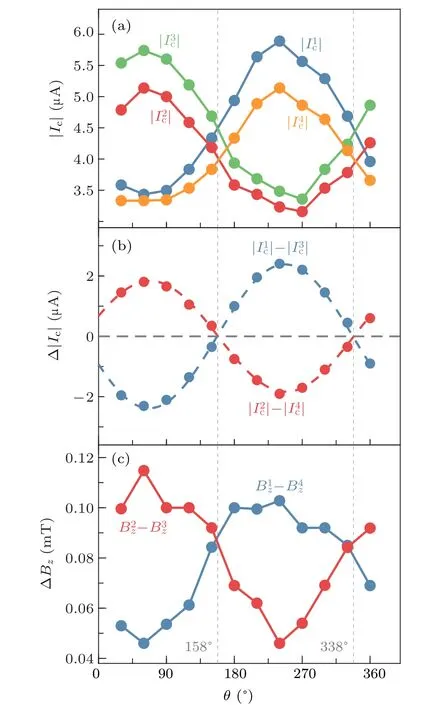
Fig. 3. Angular dependence of the position of the nodal points. (a) Absolute value of the critical current. (b)The difference of the critical currents,|I1c|-|I3c|and|I2c|-|I4c|. The dashed curves represent fits to a sine function.(c)The difference of the field at the nodal points,B2z-B3z and B1z-B4z.

First,let us discuss the reason for the symmetry breaking at zero in-plane field seen in Fig.1. One possible cause is the self-field effect.[30]For JJs with certain geometries,a nonuniform current distribution in the superconductor electrodes can produce an additional field through the junction area, which shifts the pattern horizontally. As the self-field depends on the polarity of the current,the patterns in the upper and lower half-plane shift towards opposite directions. The geometry of our JJs has a mirror symmetry about the center line along the current direction, precluding the self-field effect. Even if the device slightly deviates from the mirror symmetry due to imperfections introduced by fabrication,the skewness of the pattern should vary from device to device. The consistent shift in all devices indicates that the symmetry breaking is associated with the crystal structure of V5S8.required to break in order to break the mirror symmetries,I±c(Bz)=I±c(-Bz) andI+c(Bz)=-I-c(Bz), are listed in Table 1. Hereσx,y,zare the Pauli matrices,Px(y)is thex(y)-parity operation,Tis the time reversal operation. Disordered potentialVx(y), which is asymmetric underPx(y), unlikely plays an important role, otherwise the pattern in different devices would shift in random directions,[21]not to mention the fact that our JJs,made from a continuous aluminum film,are presumably quite uniform. In the absence of an in-plane field,two forms of SOC, Rashba SOCαand Dresselhaus SOCβ,can break most of the symmetries. It is plausible that V5S8has bothαandβor similar forms of SOC, as those SOCs are the key ingredients in the theories on the in-plane Hall effect,[34–37]which has been observed in V5S8. However,there are still two more symmetry operators left,σzPyPxandσzPxPyT, which guarantee the mirror symmetries of the pattern.

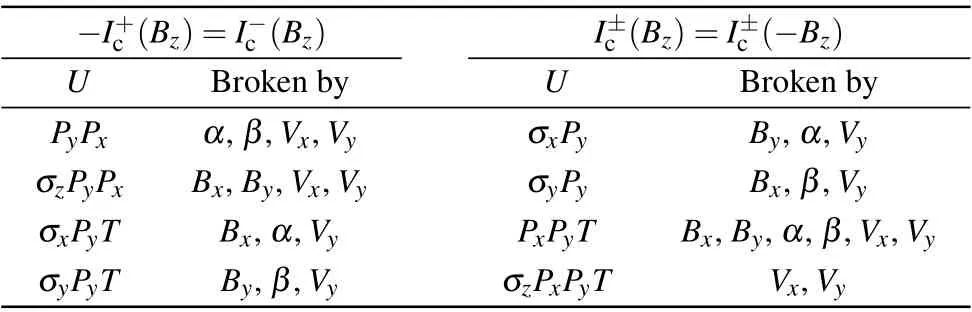
Table 1. Symmetry operations U protecting -I+c (Bz)=I-c (Bz) and I±c (Bz)=I±c (-Bz)respectively adapted with permission from Ref.[10].Copyrighted by the American Physical Society.

Abrikosov vortices in superconducting electrodes near the JJ can lead to an asymmetric Fraunhofer pattern,too.However,the effect breaks the field symmetry,I±c(Bz)=I±c(-Bz),leaving the current symmetry,I+c(Bz)=-I-c(Bz),intact,[31,32]which is at odds with our results. Moreover,we intentionally made the superconductor leads narrow enough so that vortices can not enter.[33]For comparison, when the leads are wider than 0.65 μm,jittering of the pattern due to vortex jump started to appear in the Fraunhofer pattern.

Rasmussenet al. have studied the interference pattern of a SNS JJ theoretically and related its symmetry to certain symmetries in the Hamiltonian.[10]The symmetries that are

It has been proposed that the mirror symmetries of the interference pattern,I±c(Bz)=I±c(-Bz)andI+c(Bz)=-I-c(Bz),are broken in SNS based on inversion symmetry breaking topological materials.[38]This is because the topological surface states on two sides of the JJ have different Fermi velocities, resulting in different Josephson currents. The interference pattern by the surface states is thus shifted and skewed,depending on the polarity of the current. Taken into account the dominant contribution from the bulk, the resultant inversion symmetric pattern agrees with what we observed. Broken mirror symmetries of the Fraunhofer pattern were observed in topological materials.[39,40]The difference of the Josephson currents on two sides breaks the mirror symmetry of the Josephson current spatial distribution about the center line of JJ along the current. It is worth noting that this mirror symmetry is essential for the nodal point being on theI=0 axis.Therefore, the finite critical current of the nodal point in our data provides additional evidence, independent of the model on inversion symmetry breaking topological materials,that the Josephson currents on the two sides are not equal.

The asymmetry of the pattern is tuned by the in-plane field, seen in Fig. 2. It has been shown that an in-plane field can suppress the Josephson current in the center of a JJ via a peculiar flux focusing effect.[21]Consequently, the zero field critical current is reduced and the interference pattern becomes more like that of a superconducting quantum interference device. It works when the field is parallel to the current and does not depend on the field polarity. As the field is rotating in the plane,a period ofπis expected in the angular dependence of the critical current, in contrast to a period of 2πshown in Fig.3. Furthermore,the effect does not depend on the polarity of the current, so it will not break aforementioned two mirror symmetries of the pattern. At last,the flux focusing effect maximizes atθ=0°and 180°, whereas the critical currents of the nodal points at these two angles are at neither the maximum nor the minimum, shown in Fig. 3. These distinctions rule out the flux focusing effect of the in-plane field.

An in-plane field usually acts on electrons by the Zeeman effect,thus its strong influence on the pattern suggests that the asymmetry is related to the spin. In the case of inversion symmetry broken topological materials, the Zeeman effect will break the time reversal symmetry of the surface states,which alters the Josephson current on the two sides. The change in the current distribution inevitably leads to a change of the pattern. The critical angles ofθ=158°and 338°, at which the inversion symmetry of the pattern is restored,are probably related to the particular form of SOC in V5S8.

The unusual symmetry in the Fraunhofer pattern of Al–(Al/V5S8)–Al Josephson junctions suggests an anomalous Josephson coupling stemming from the SOC in heterodimensional superlattice V5S8. This newly discovered compound,with its exotic SOC and the ability of forming a homointerface Josephson junction,offers an intriguing platform for investigation of unconventional Josephson effects and superconductivity.

Supporting information

The measurements of the in-plane field dependence of the Fraunhofer pattern on another Al–(Al/V5S8)–Al Josephson junction S2 are given in the supporting information.

Acknowledgements

Project supported by the National Key Basic Research Program of China (Grant No. 2016YFA0300600) and the National Natural Science Foundation of China (Grant Nos.11574005 and 11774009).