An apodized cubic phase mask used in a wavefront coding system to extend the depth of field
Lina Zhu(朱麗娜), Fei Li(李飛), Zeyu Huang(黃澤宇), and Tingyu Zhao(趙廷玉)
Department of Physics,Key Laboratory of Optical Field Manipulation of Zhejiang Province,Zhejiang Sci-Tech University,Hangzhou 310018,China
Keywords: apodized cubic phase mask,wavefront coding,depth of field,image restoration
1. Introduction
For traditional imaging systems,the sharpness of the image is greatly affected by defocus,which is limited by the lens aperture.An image system of extended depth-of-field can provide more information. Thus the technology of extension of depth of field is widely applied in many imaging systems,including biomedical imaging systems,[1]microscopes,[2,3]and infrared imaging systems.[4,5]
For wavefront coding systems,a phase mask(PM)is introduced into the pupil plane to yield a long focusing line,which leads to defocus-invariant imaging properties.[6]So far,a lot of PMs have been designed to realize the extension of the depth of field, such as the cubic phase mask (CPM),[7]the sinusoidal phase mask,[8]the exponential phase mask,[9]the logarithmic phase mask,[10]the polynomial mask,[11]the Jacobi–Fourier phase mask,[12]the tangent phase mask,[13]the free-form phase mask,[14]the rational phase mask,[15]the chiral phase mask[16]and the high-order phase mask.[17]The PMs used in wavefront coding system can generate blurred but defocus-insensitive images,which can be digitally restored to sharp images.
Generally,the point spread function(PSF)caused by the PMs mentioned above has the problem of big side-lobes.[18]The side-lobes of the PSF in spatial domain result in the decay of the modulation transfer function (MTF) in frequency domain. This causes low-contrast and ringing effect in image restoration. CPM is applied as an example here to be modified to suppress the side-lobes because it is one of the most classic and widely-used PMs.
The paper is organized as follows. Section 2 proposes the theoretical analysis of the wavefront coding system with the CPM and the apodized CPM.The simulation and experimental results are shown in Section 3. Finally,the conclusions are presented in Section 4.
2. Theoretical analysis
A CPM is usually described as[19]

wherebis the truncation parameter along thexaxis. Notice that the apodized CPM becomes the classic CPM whenb=1.
Take the defocus aberrationφinto consideration.[20]The pupil functionP(a,b,x,y,φ)of the system can be expressed as

and then the PSFh(a,b,x′,y′,φ)can be calculated as


Fig.1. Phase profile of: (a)the CPM of a=19.9925;(b)the apodized CPM of a=21.6188 and b=0.5760.
The parameters of the PMs should be optimized to obtain a good performance in the design of a wavefront coding system. There are various merit functions in the optimization,such as Fisher information (FI), mean square error (MSE) of PSF or MTF. However, the merit function should take consideration of the defocus-insensitivity and the informationpreservation. The consistency of the MTF surfaces of different defocus, reflecting the defocus-insensitivity, is chosen as the target function of optimization. The volume MTF surfaces and the coordinate plane encircled,reflecting the informationpreservation, is used as the constriction function of the optimization.Then the merit function of optimization is illustrated as

whereTHis the threshold of the constriction function.[21,22]
Simulated annealing algorithm[23]is used as an optimization algorithm with the assumption of maximum defocusφmax=30 andTH=0.1. The optimal parameter for the CPM isa=19.9925,while the parameters of the apodized CPM area=21.6188 andb=0.5760. The phase profile of the optimal CPM and the apodized CPM are given in Fig.1.
2.1. The simulation and experiment
By using Eq. (4), the PSFs of the wavefront coding system with the optimal CPM (a= 19.9925) under the conditions of different defocus aberrationsφ ∈[0,15,30]are shown in Fig. 2(a). The PSFs of the traditional ideal imaging system with no PM are given in Fig. 2(a) for comparison. The PSF of the traditional system is rectangular since the pupil is assumed to be rectangular. The image quality deteriorates steadily as the defocus aberration increases. As a contrast,PSFs of the wavefront coding system using the apodized CPM(a=21.6188,b=0.5760)are shown in Fig.2(b). The PSFs of the traditional system with the apodized pupil(b=0.5760)are also given in Fig. 2(b). The difference between the traditional systems in Figs. 2(a) and 2(b) is the size of the pupil.The former is the same of the one using the CPM (b=1),while the latter is the same of the one using the apodized CPM(b=0.5760). The PSFs of the wavefront coding systems with either CPM or apodized CPM change little as the defocus increases, thus both of them are almost insensitive to defocus,which means both of them are able to extend the depth of field.However,there are two improvements of the PSFs of the system with the apodized CPM compared the one with the CPM.Firstly, the size of the PSF is smaller, leading to the energy concentration. Secondly,the side-lobes are suppressed,which means most of the energy is focused on the vertex of the PSF.The energy concentration contributes to a good image restoration.
Furthermore,the tangential and sagittal MTFs of the systems with different pupil masks under the conditions of different defocus aberrationsφ ∈[0,15,30]are shown in Figs.3 and 4. The MTFs of the traditional system with no PM decay fast as the defocus aberration increases along with zero points appeared in either sagittal plane or in tangential plane as shown in Fig. 3. It indicates that some information of the defocused traditional system is lost and cannot be restored in any way.However,the cut-off frequency of the traditional system with apodized pupil is smaller in sagittal plane as shown in Fig. 3(b). In comparison, the systems with the CPM and the apodized CPM are defocus-insensitive as shown in Fig.4.This is the foundation of the image restoration using one PSF as the deconvolution core.The MTF curves of the system with the apodized CPM are higher than the one with the CPM in tangential plane as shown in Fig.4(a).
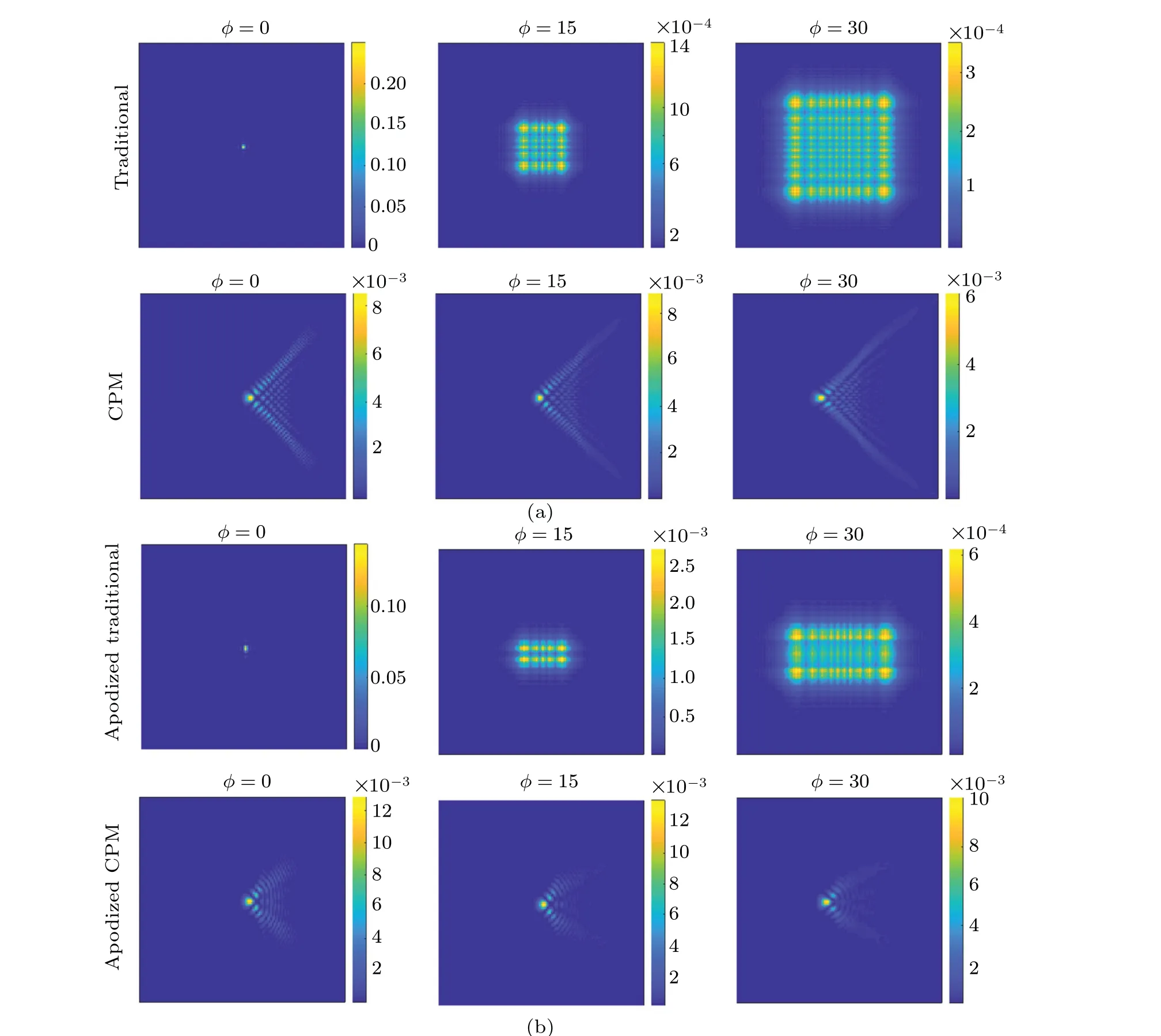
Fig.2. The PSFs of the systems under the conditions of different defocus aberrations with: (a)no PM and the CPM;(b)the apodized pupil and the apodized CPM.
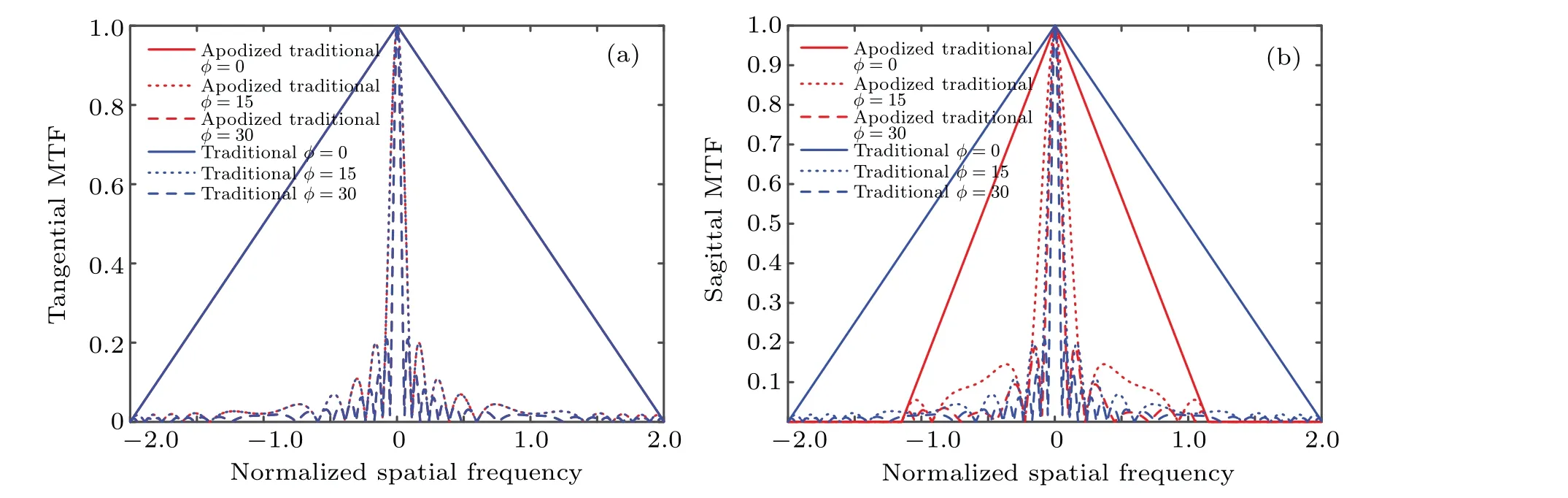
Fig.3. The MTF curves of the traditional systems with the no PM(blue)and the apodized pupil(red)under the conditions of different defocus aberrations: φ =0(solid line),φ =15(dotted line),and φ =30(dashed line)in(a)tangential plane;(b)sagittal plane.

Fig. 4. The MTF curves of the system with the CPM (blue) and the apodized CPM (red) under the conditions of different defocus aberrations: φ =0(solid line),φ =15(dotted line),and φ =30(dashed line)in(a)tangential plane;(b)sagittal plane.
Compared to the system with CPM,although the cut-off frequency of the system with apodized CPM is smaller in sagittal plane,the MTF curves are higher in low-and-medium frequency domain. In fact,the MTF in high frequency domain is so low that it even can reach to the same order of the noise. Thus the higher MTF in low-and-medium frequency domain takes a more important role than the smaller cut-off frequency in image restoration.ditional system with apodized pupil and the wavefront system with apodized CPM under the conditions of different defocus aberrations are shown in Fig.6. The system of the wavefront coding system with the apodized CPM has a better image quality than the traditional one with the apodized pupil when the defocus aberration increases. Compared to the system with the CPM,the noise is decreased greatly and the ring-effect is suppressed effectively in the system with the apodized CPM.Furthermore, the contrast is enhanced. This suggests that the system with the apodized CPM has a better quality of image restoration than the one with the CPM.
Wiener filter,[24]one of the classical algorithms, is applied in image restoration of the wavefront system here. The frequency spectrumX(u,v,φ) of the restored image is described as
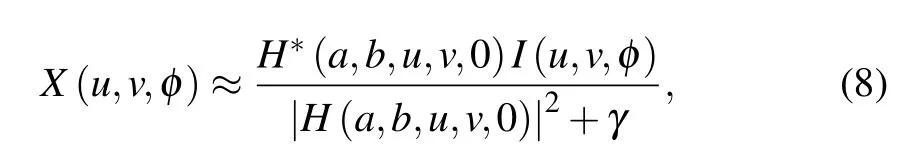
whereγis signal-to-noise ratio,I(u,v,φ) represents the frequency spectrum of the image to be restored,H(a,b,u,v,0)is the focused OTF,which can be calculated by the Fourier transform of the focused PSF,andH*(a,b,u,v,0)is the conjugation of the focused OTF.
A spoke is used as an object here. Figure 5 shows the images of the traditional optical system with no PM and the wavefront system with CPM under the conditions of different defocus aberrationsφ=0(the first column),φ=15(the second column), andφ=30 (the third column). For traditional system with no PM,it is distinct that the image gets more and more blurred as the defocus aberration increases as shown in Fig.5(a). The restored images of the wavefront coding system are sharp despite of the defocus aberrations.However,the contrast deteriorates. The framed parts in Fig. 5(a) are enlarged in Figs. 5(b) and 5(c) for further analysis. Unfortunately, the ring-effect is introduced into the restored images of the wavefront coding system. For comparison, the images of the tra-
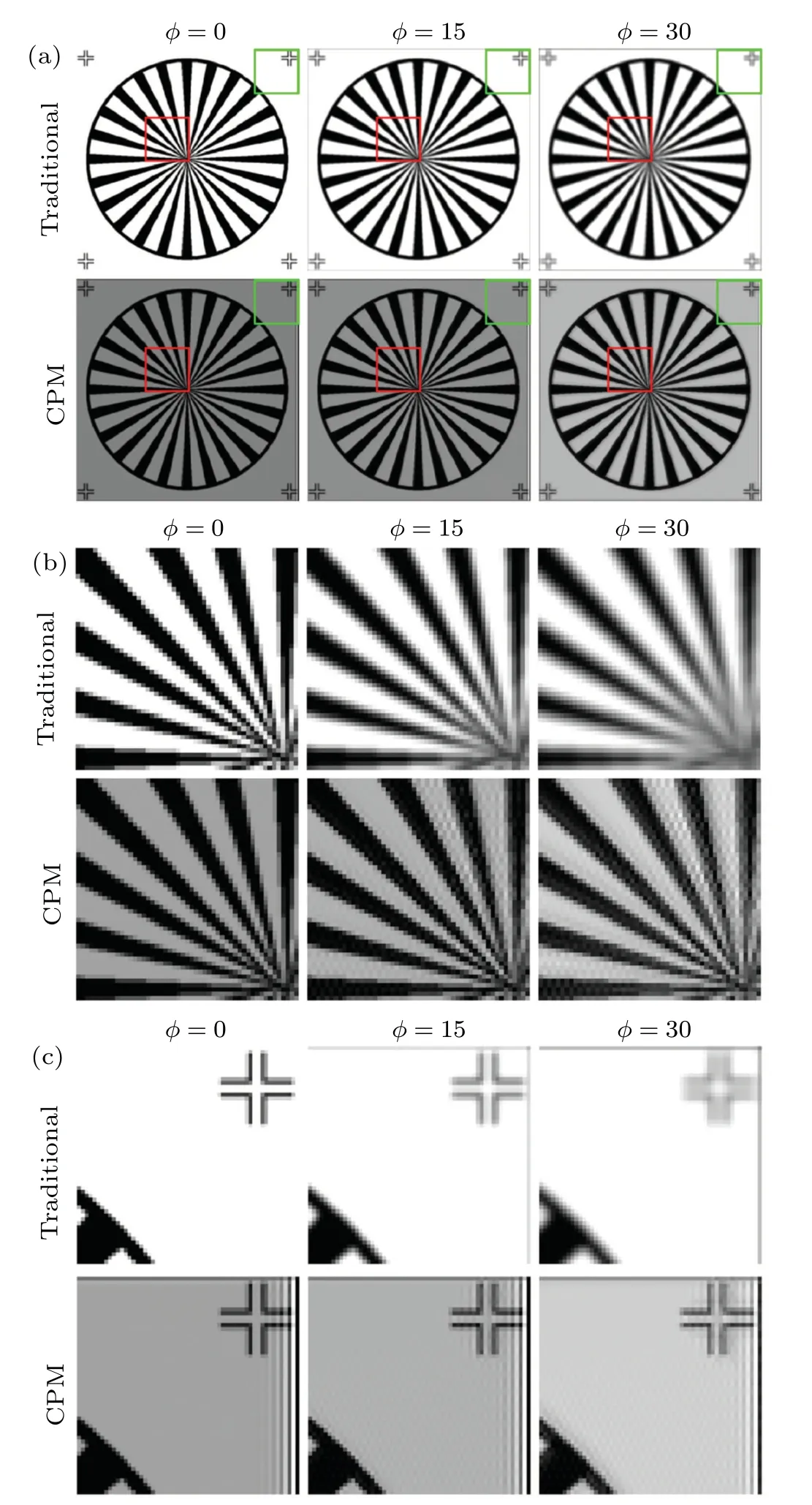
Fig.5. Simulation images with spokes target of the system with: (a)no PM and the CPM. (b) The enlarged frame of the spoke with red rectangle. (c)The enlarged frame of the spoke with green rectangle under the conditions of different defocus aberrations:φ=0(the first column),φ=15(the second column),and φ =30(the third column).

Fig.6. Simulation images with spokes target of the system with: (a)the apodized pupil and the apodized CPM;(b)the enlarged frame of the spoke with red rectangle;(c)the enlarged frame of the spoke with green rectangle under the conditions of different defocus aberrations: φ =0(the first column),φ =15(the second column),and φ =30(the third column).
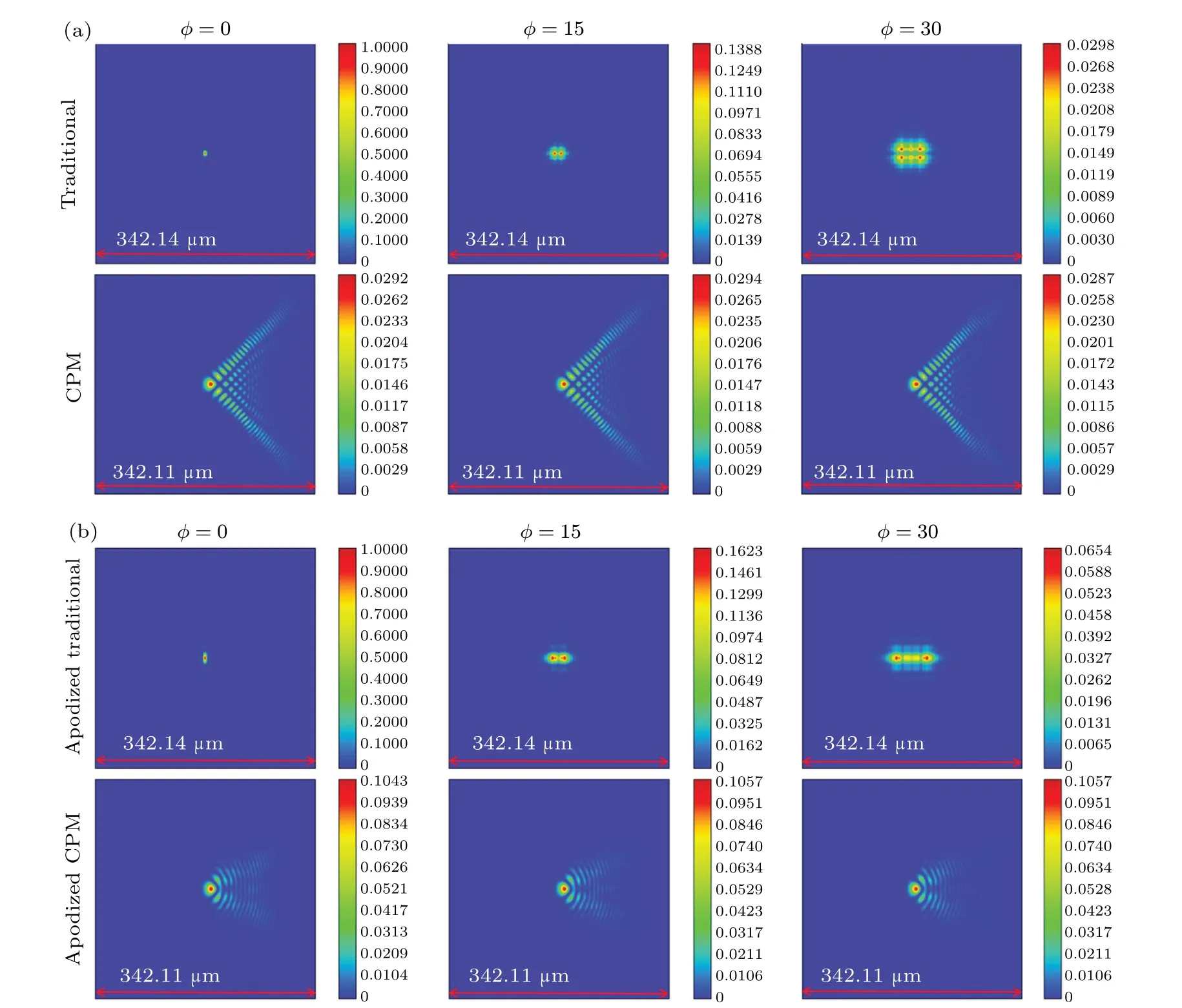
Fig.7. The PSF diagrams in ZEMAX simulation: (a)the traditional optical system using no PM and the wavefront coding system using the CPM; (b) the traditional optical system using apodized pupil and the apodized CPM under the conditions of different defocus aberrations:φ =0(the first column),φ =15(the second column),and φ =30(the third column).
The advantages of the system with the apodized CPM over the CPM is verified by the optical simulation with Zemax, a commercial optical design software. A phase mask is added on the pupil of a singlet,whose focal length is 150 mm.
As mentioned above, PSF reflects the imaging capability of an optical system. The PSFs of the traditional optical system with no PM and the wavefront coding system using CPM under the conditions of different defocus are shown in Fig.7(a). The PSF becomes large with the increase of defocus in the traditional system,while the PSF changes little with the defocus in the wavefront coding system using the CPM. As contrast, PSF of the traditional optical system with apodized pupil and the wavefront coding system using the apodized CPM is shown in Fig. 7(b). Similarly, the PSF changes little with the defocus in the wavefront coding system using the apodized CPM.Compared to the PSF of the wavefront coding system using the CPM,the size of the PSF is significantly reduced and the side-lobes of the PSF is effectively suppressed in the system using the apodized CPM.Notice the value of the colorbar in Fig.7. It is obvious that the energy of the PSF is more concentrated in the system using the apodized CPM.
The diagram of the experimental wavefront coding system is shown in Fig.8. A laser with a wavelength of 632.8 nm is used in as a light source. A 100×microscope objective and lens 1 compose a beam expander. Lens 2 with the aperture of 1 inch and the focal length of 150 mm is applied as the imaging lens. The phase mask is placed in the pupil plane of the system, which located in front of lens 2. The phase mask is realized by a liquid crystal spatial light modulator(HEO0017,HOLOEYE)and a polarizer and an analyzer. The CCD camera with 2560×1920 pixels,whose size is 3.4 μm×3.4 μm,is used to capture images. The position of the CCD can be adjusted along the optical axis to change the defocus aberration.
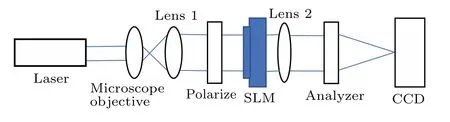
Fig.8. Diagram of the experimental wavefront coding system.
The PSFs under the conditions of different defocus aberrations are shown in Fig. 9. The experimental results verifies the analysis and simulation results. Compare the PSF of the wavefront coding system with the CPM to the one of the system with the apodized CPM. Obviously, both of them are insensitive to the defocus. However, the size of latter is smaller than the former. Furthermore,more energy is retained in the vertex in the latter than the former. It is helpful in image restoration.

Fig.9. Experimental PSFs of the wavefront coding system using the CPM(the first row)and the apodized CPM(the second row)under the conditions of different defocus aberrations: φ =0(the first column),φ =15(the second column),and φ =30(the third column).
3. Conclusion
A novel apodized cubic phase mask proposed here to be used as a phase mask to extend the depth of field in a wavefront coding system. Compared to the classic cubic phase mask, the apodized CPM has a similar capacity of depth of field extension. However, the size of the PSF is significantly smaller and the energy is more concentrated. These characteristics enhance the contrast and reduce the ringing effect in image restoration. These conclusions are verified by the simulation and experimental results. The apodization of the phase mask can be used in not only cubic phase mask,but also other phase masks such as the sinusoidal phase mask,the exponential phase mask, and the logarithmic phase mask. Thus this technology can be applied to kinds of imaging system to extend the depth of field and improve the imaging quality, such as infrared image system,microscopies,and cameras.
- Chinese Physics B的其它文章
- A nonlocal Boussinesq equation: Multiple-soliton solutions and symmetry analysis
- Correlation and trust mechanism-based rumor propagation model in complex social networks
- Gauss quadrature based finite temperature Lanczos method
- Experimental realization of quantum controlled teleportation of arbitrary two-qubit state via a five-qubit entangled state
- Self-error-rejecting multipartite entanglement purification for electron systems assisted by quantum-dot spins in optical microcavities
- Pseudospin symmetric solutions of the Dirac equation with the modified Rosen–Morse potential using Nikiforov–Uvarov method and supersymmetric quantum mechanics approach

