Jie Shen(沈潔) Xitong Xu(許錫童) Miao He(何苗) Yonglai Liu(劉永來)Yuyan Han(韓玉巖) and Zhe Qu(屈哲)

1Anhui Province Key Laboratory of Condensed Matter Physics at Extreme Conditions,CAS Key Laboratory of Photovoltaic and Energy Conservation Materials,High Magnetic Field Laboratory,Hefei Institutes of Physical Science,Chinese Academy of Sciences,Hefei 230031,China

2Science Island Branch of Graduate School,University of Science and Technology of China,Hefei 230026,China

Keywords: geometrical frustration,van der Waals material,spin freezing

1. Introduction

Geometrical frustration, defined as situations where interactions between neighboring spins cannot be energyminimized simultaneously,[1]often appears in triangular,face-centered cubic, hexagonal close-packed and kagome lattices.[2–6]Such geometrical frustration can lead to many novel phenomena by suppressing conventional magnetic orders,[7–10]including highly degenerate ground states,strong fluctuations,cooperative paramagnetism,spin disordered state at low temperature,etc.[11–16]In particular, the triangular lattice in two dimensions (2D) is the simplest and the first proposed structure of geometrical frustrated systems due to a single magnetic ion per unit cell.[17]A lot of three-dimensional materials with triangular magnetic lattice have been investigated,such as Gd2PdSi3,[18]CuFeO2,[19]LuCoGaO4,[20]and Ca3CoNb2O9,[21]but only a few van der Waals(vdWs)triangular magnets have been investigated, where the interplay of low dimensionality and spin frustration may lead to the emergence of exotic physical properties.

TheTM2X4(T=Ni/Fe;M=Ga/Al;X=S/Se)is one of the few systems that possess the vdWs 2D triangular geometry with the magnetic transition metal sublattice.Among them,NiGa2S4is a typical bulk-insulating antiferromagnet with an exact triangular lattice. Combined magnetic susceptibility,specific heat and neutron-diffraction experiments have shown no long-range order; instead nanoscale quasi-static correlation is found, indicating that geometrical frustration can stabilize a low temperature spin disordered state with coherence beyond the two-spin correlation length.[2,22,23]The magnetic specific heat at low temperatures showsT2power law, indicating a 2D gapless linearly dispersive mode.[24]The isostructural FeGa2S4and FeAl2Se4,where the transition Fe2+ion has a spinS=2 that is twice larger thanS=1 for Ni2+, exhibit a similar spin disordered state at low temperatures.[25–28]It is further suggested that the integer spin size is crucial for the existence of such spin wave excitations,since Zn2+(S=0)and Fe2+(S=2)substitutions in NiGa2S4retain the same feature while Co2+or Mn2+substitution does not.[29]

Instead of substituting the basal transition metal,an alternative way is to explore the quantum physics of the bilayer system in the related compounds.[24,30–32]Fe2Ga2S5is the homologous compound ofTM2X4.The bilayer Fe atoms form a kind of distorted honeycomb lattice with strong super-exchange interaction mediated by sulfur,leading to a long-range antiferromagnetic order atTN=113 K.[24,33]Based on the difference between the 124 and 225 compounds, it was suggested that geometrical frustration in quasi-2D triangular systems is crucial for the spin disordered state.[24]However,whether bilayerT2M2X5systems or half-odd integer spins exclude these spindisordered states remains an open question.

In order to investigate bilayering effect and half-odd integer spin in stabilizing the spin disordered state,we searched and have succeeded in synthesizing single crystals of the homologous Mn2Ga2S5. Using combined magnetism and heat capacity measurements,we find that Mn2Ga2S5exhibits a spin freezing transition at 12 K,well below itsθw～-260 K.This spin freezing behavior is a result of the competition between exchange interactions and the bilayered 2D crystalline structure. Our results suggest that the layered Mn2Ga2S5would be a good candidate for investigating the physics of 2D magnetism and spin disordered state.

2. Experimental method

Single crystals of Mn2Ga2S5are synthesized by the chemical vapor transport (CVT) method. High-purity elements Mn,Ga and S with stoichiometric molar ratio of 2:2:5 are mixed and put into the quartz ampoule. Iodine(3 mg/cm3)is used as the transport agent. The ampoule is vacuum sealed and placed in a two-temperature-zone tube furnace with a temperature gradient of 1050–950°C for 7 days, then cooled down to room temperature naturally. As shown in the inset of Fig. 1(c), large amounts of dark brown single crystals which are soft and easily exfoliated can be obtained for each trial.Direct reaction of the stoichiometric elements at 1050°C also leads to the formation of well faceted crystals,yet they always encapsule large amounts of unreacted sulfur.

Crystals grown by CVT are grounded into powder for the x-ray diffraction (XRD) characterization. XRD patterns are collected at room temperature on a Rigaku MiniFlex powder diffractometer using filtered Cu-Kαradiation. The chemical composition of Mn:Ga:S is also measured by energy dispersive x-ray(EDX)spectrum. The dc and ac magnetic susceptibilities are measured from room temperature down to 2 K with a superconductive quantum interference device(SQUID).Specific heat of Mn2Ga2S5single crystals is mainly characterized in a Quantum Design physical property measurement system(PPMS-14T).

3. Results and discussion

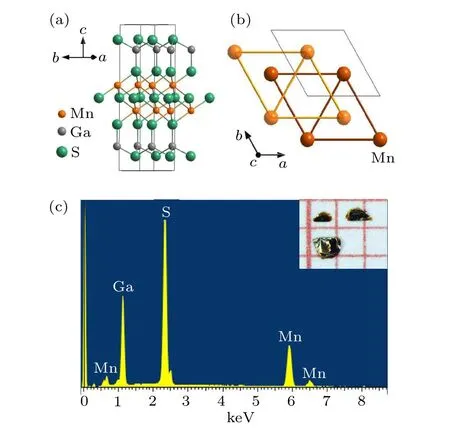
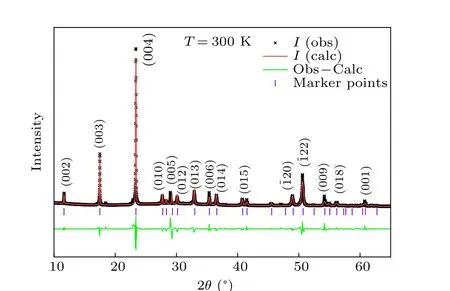
Mn2Ga2S5belongs to the space groupPˉ3m1. As shown in Fig.1,it possesses a layered triangular structure that can be described as slabs of two GaS layers and one central Mn2S3layer. The Mn2+ion, forming two sets of triangle sublattice,adopts an electronic configuration t32ge2gthat gives rise to a high spin state withS=5/2 local moment. The top and bottom sheets of GaS4tetrahedra are connected by the central Mn2S3layer of edge-sharing MnS6octahedra. Along the crystallographiccdirection,the tri-layered unit is separated by typical vdWs gaps. Figure 1(c)shows EDX results of our single crystals. The element molar ratio of Mn:Ga:S=2:2.06:5.31 is very close to its stoichiometric value. The powder XRD results are shown in Fig. 2. The refined lattice parameters area=3.718 °A andc=15.242 °A, close to previous parameters reported for polycrystal Mn2Ga2S5.[34]

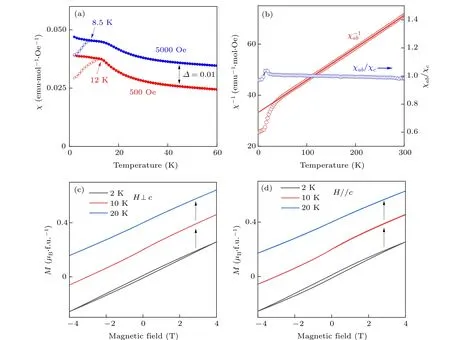
We start by performing dc magnetization measurements on Mn2Ga2S5. Figure 3(a) depicts the temperaturedependence of the magnetic susceptibility measured at applied magnetic fields of 500 Oe and 5000 Oe oriented perpendicular to thecaxis with both zero-field-cooling(ZFC)and fieldcooling (FC), respectively. Both FC and ZFC curves show highly coincident behavior above 12 K. At 500 Oe, the ZFC and FC curves bifurcate atTf=12 K for both in-plane and out-of-plane (not shown here) directions, indicating a spinfreezing transition. Unlike NiGa2S4or FeGa2S4,[24]this feature withstands relative strong magnetic fields. We find that the bifurcation at 5000 Oe shifts to 8.5 K with increasing fields, while the bending around 12 K can still be observed.In the high temperature region,the magnetic susceptibility decreases rapidly. As shown in Fig. 3(b), the inverse magnetic susceptibility 1/χis linear above 150 K,suggesting a Curie–Weiss paramagnetic state. There is a downward curving in the 1/χprofile below 50 K,which is due to the formation of spin clusters.[35]By fitting the high temperature linear part of 1/χabto the Curie–Weiss law

withCbeing the Curie constant andθwthe Curie–Weiss temperature,the effective moment is fitted asμeff=5.597μB/Mn,close to the expected value(5.92μB)for high spin Mn2+ions withS=5/2.θwis estimated to be as high as-260 K,leading to an empirical frustration index off=-θw/Tf≈22.The value is much larger than those in the homologous triangular spin-freezing systems NiGa2S4and FeGa2S4(around 10[24]),revealing that the sample is strongly frustrated.[36]The anisotropic ratioχab/χcis closed to 1 for all temperatures,suggesting the overall interaction between Mn2+is almost Heisenberg type.

Figures 3(c) and 3(d) show the field dependence of the magnetization at representative temperatures. The magnetization is not saturated at 7 T. When the magnetic field is along thecaxis, we observe a small field hysteresis loop around±4 T which fades away above 5 K.The saturation magnetization for this low temperature ferromagnetic component is estimated to be around 0.025μB/Mn,about 0.4%of the effective moment. An intuitive thinking is the inclusion of some magnetic impurity phase in the samples. However,possible impurity phases like MnGa2S4,MnS,MnS2,Mn2O3,etc. all haveTC/TNwell above 10 K,[37–40]whereas the hysteresis loops in our samples could only be observed below 5 K. We cannot rule out the possibility of an intrinsic,field induced weak ferromagnetism as competition between frustration and exchange interaction inside the vdWs bilayers may mimic some kind of canted antiferromagnetism.

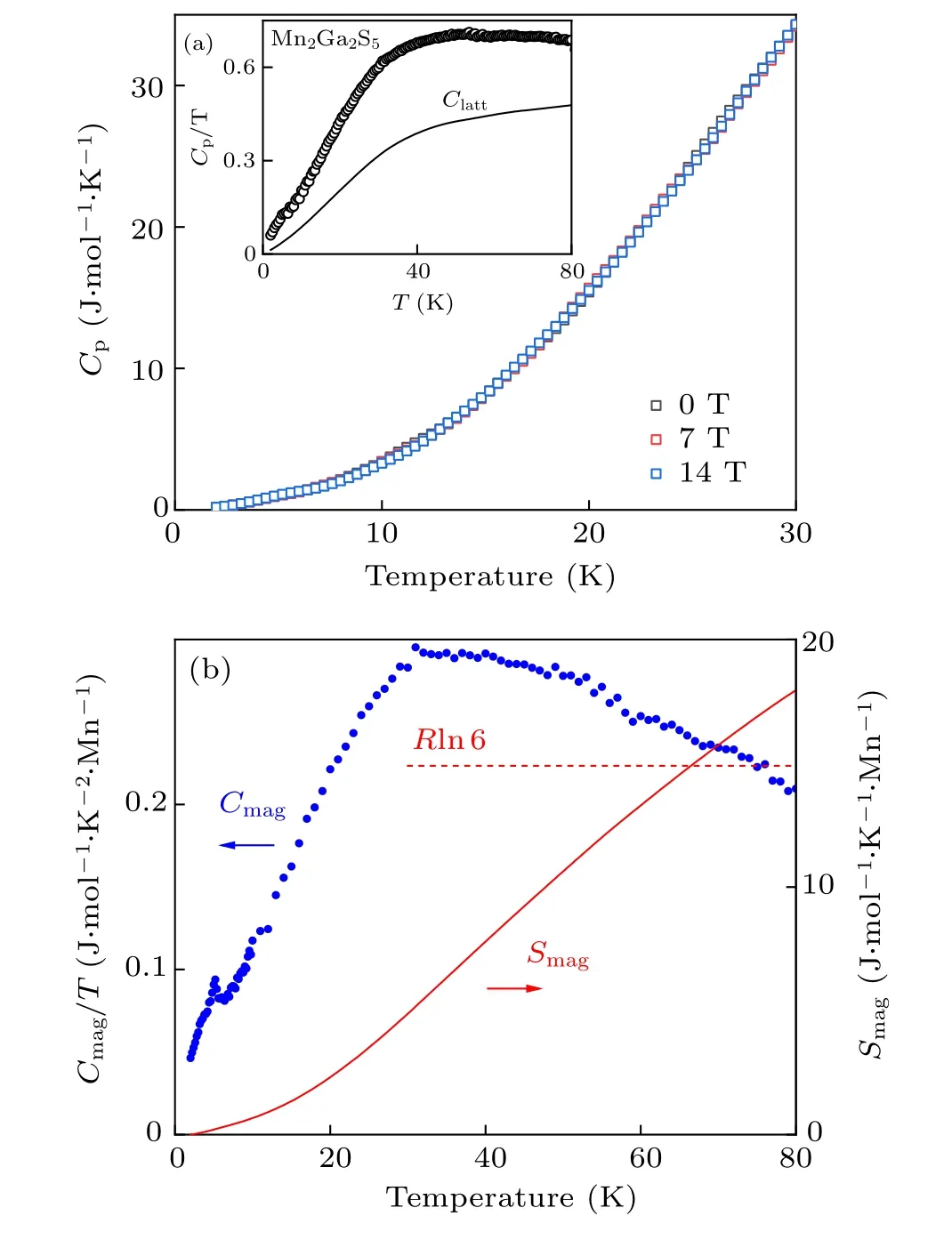
To shed light on the nature of magnetic ordering in the Mn2Ga2S5,we also measure its specific heat in Fig.4(a). The specific heatCpshows neither aλ-like anomaly or any transition features aroundTf=12 K, which is consistent with features of spin glasses. The curves are also identical with different applied magnetic fields up to 14 T,meaning that the spindisordered states are very insensitive to fields. As Mn2Ga2S5is a layered chalcogenide magnetic semiconductor/insulator,the electronic contribution to specific heat which arises from free charged carriers should be negligible. The specific heat of Mn2Ga2S5therefore consists of the lattice partClattand magnetic contributionCmag, which is expressed by the following formula:[41,42]

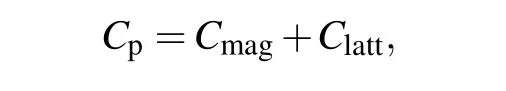
whereCmagis the magnetic contribution to specific heat. For a rough estimation of the lattice contributionClatt, the specific heat of the homologous nonmagnetic material Zn2In2S5is used as a reference.[24]TheClattof Mn2Ga2S5is related to that of Zn2In2S5by a scale factorΘD(T)∝M-1/20V-1/30, whereΘD(T),M0andV0are the Debye temperature,the molar mass and volume,respectively.[2]As shown in Fig.4(b),Cmag/Tof Mn2Ga2S5shows one broad peak at around 30 K,corresponding to the release of magnetic entropy above the spin-freezing transition. This is unlike the case ofTM2X4where Goldstonetype spin waves from 2D gapless linearly dispersive modes contribute another peak belowTf.[24,26,27]This substantial difference should arise from the complex exchange interaction host in the bilayered Mn lattice.Compared with the simple triangularTsublattice inTM2X4, Mn2Ga2S5possesses two extra interlayer coupling paths among Mn–S–Mn atoms: nearly rectangular paths between the nearest neighbor(NN)Mn sites and 180°paths connecting the second NN Mn sites. In this bilayer structure,these bonds happen to form four sublattices of a buckled honeycomb lattice.[24]According to theJ1–J2model on the honeycomb lattice,[43]the system exhibits Neel magnetic order atJ2/J1?0.2 and collinear type atJ2/J1?0.4,while in the intermediate region a disordered ground state is expected. As no long-range order has been detected,the coupling in Mn2Ga2S5seems to be within this intermediate region.

In Fig. 4(b), we also observe a tiny peak around 5 K,which is also field independent up to 14 T. As we discuss above, this may be either from some impurity phase or from inherent weak ferromagnetism corresponding to the ferromagnetic-like component inM–Hcurves in Figs.3(c)and 3(d),which deserves further studies in future.

We also estimate the magnetic entropySmagusing the following thermodynamic relation:As shown in Fig.4(b),Smagappears to be larger than the theoretical total entropyRln(6)forS=5/2 spin degree of freedom. This may be due to the involvement of orbital degree of freedom due to holes in the t2gorbitals,similar to the case of FeGa2S4.[24]

Finally we discuss the ac magnetic susceptibility of Mn2Ga2S5at temperatures near the spin freezing temperature.Figure 5(a)shows the temperature dependent ac susceptibility from 13.7 Hz to 417 Hz, which is probed by a fixed ac magnetic field of 10 Oe. A peak reflecting the spin freezing temperatureTfis observed in the real part of the ac susceptibility,which shifts towards high temperatures with the enhanced ac frequency. In the empirical Vogel–Fulcher law,[44,45]Tfand the frequencyfis related by

whereτ0,Ea,andT0are the intrinsic relaxation time,the activation energy of the process, and the ideal glass temperature,respectively. As shown in Fig. 5(b),Tfis clearly linear with respect to-1/ln(τ0f). The deducedEa/(kBT0)～5 is much larger than 1, confirming Mn2Ga2S5is unlike a canonical spin glass.[46]The shift of the peak temperature with respect to frequency can also be described by the Mydosh parameter(ΔTf)/(TfΔlogω).[47]The obtained value for Mn2Ga2S5is 0.027 which is also larger than expected for a canonical spin glass(0.005 for CuMn and 0.0045 for AgMn).[44]

4. Conclusion

We report the dc and ac magnetic susceptibility and specific heat measurements of the vdWs material Mn2Ga2S5featuring bilayered Mn triangular lattice. It is found that Mn2Ga2S5exhibits no long-range order down to 2 K.A spin freezing transition, which is observed as the bifurcation between field-cooling and zero-field-cooling dc magnetization and enhanced frequency dependence of ac magnetization,occurs at around 12 K, well below the Curie–Weiss temperatureθw～-260 K. This yields a frustration index off=-θw/Tf≈22, indicating the system is highly frustrated. The Mydosh parameter obtained from ac susceptibility measurements is also larger than what is expected for a canonical spin glass. The absence of a double-peak structure in magnetic specific heat compared with theTM2S4compounds implies that the spin freezing behavior in Mn2Ga2S5is a result of the competition between exchange interactions and the bilayered 2D crystalline structure. The high magnetic interaction and strong frustration make Mn2Ga2S5a good candidate for studying the spin disorder state and the application of 2D layered magnetic material. Further neutron scattering measurement,nuclear magnetic resonance and muon spin resonance experiments can be useful to reveal detailed formation mechanism of the spin disorder state.

Acknowledgment

Project supported by the National Natural Science Foundation of China(Grant Nos.U1832214,11774007,U2032213,and 12104461).