Xu Wang(王旭) Zhi-Ping Wang(王志萍) Feng-Shou Zhang(張豐收) and Chao-Yi Qian(錢超義)

1Department of Fundamental Courses,Wuxi Institute of Technology,Wuxi 214121,China

2The Key Laboratory of Beam Technology and Material Modification of Ministry of Education,College of Nuclear Science and Technology,Beijing Normal University,Beijing 100875,China

Keywords: time-dependent density functional theory,cytosine,proton-induced collision,fragmentation

1. Introduction

Understanding of irradiation damage of biologically relevant molecules on the nanoscale is an active interdisciplinary research field and is an important prerequisite for ion beam cancer therapy.[1–8]In recent years, the ionization and fragmentation of DNA/RNA base molecules in collision with charged projectiles have attracted more and more attention because of their growing radiobiological importance. It is necessary to fully understand the series of events that occur when high-velocity radiation beams interact with the biological matter. In order to improve understanding and prediction ability of harmful properties of the ionizing radiation, many efforts have been devoted to investigating the elementary reactive processes occurring during the initial radiation attack and afterwards at the molecular level.[9–16]These studies have shed light on the understanding of the ionizing radiation of biomolecules impacted by energetic ions. In contrast to the studies of high-energy proton-induced process, investigation concerning low-energetic proton interactions with DNA and its constituents are rather scarce,and a number of details have not yet been investigated. This is particularly inspired by the finding that the reactions of free secondary electrons with ballistic energies between 1–20 eV, even at energies well below ionization thresholds, induce substantial yields of single-and double-strand breaks in DNA.[3]

In theory, time-dependent density functional theory(TDDFT) emerges as a powerful tool to study the full dynamics of collisions involving complex systems since it is capable to account for many-body problems in a consistent way.[17]The approach of TDDFT coupled non-adiabatically to molecular dynamics (MD)[18](TDDFT-MD) has been applied as an effective tool in exploring ion–molecule collision dynamics.[19–26]In this paper, the TDDFT-MD implemented in the code package PWTELEMAN developed by Toulouse–Erlangen group[27–29]is used, which has been applied as an effective tool in exploring ion-molecule collision dynamics.[30–33]Encouraged by these successful studies, we are devoted to investigating the collision process of cytosine impacted by slow proton in the microscopic way.

The paper is organized as follows.In Section 2,a brief explanation of the theoretical and numerical approach is given.In Section 3,the calculated results are discussed. Finally,the conclusions are drawn in Section 4.

2. Theory and computational details

A brief description of TDDFT-MD is given here.The system is composed of valence electrons described with TDDFT and ions treated as classical point particles. Ions, which are composed of the inner shell electrons and their parent nuclei, are coupled nonadiabatically to electrons. The singleparticle wave functions{φj(r),j= 1,...,Nel}are used to describe valence electrons (Nelis the total number of valence electrons). The spatial coordinates of ions are{RI,I=1,...,Nion}(Nionstands for the total number of ions). The real-time propagation of single-particle wave functions are performed on the basis of time-dependent density functional theory(TDDFT)governed by the time-dependent Kohn–Sham(TDKS)equations[34]given as

whereρ(r,t) is the electron density given byρ(r,t) =∑j|φj(r,t)|2. In Eq. (2),Veff[ρ(r,t)] is composed of four parts,which are the electron-ion potentialVne,the Hartree potentialVH,the exchange–correlation(xc)potentialVxc,and the external potentialVext(r,t). In this study, the parameterization of Perdew and Wang[35]is applied for xc functional in the calculations, which is adequate for the present purpose. An average-density self-interaction correction(ADSIC)[36]is employed to put the single-particle energies at their correct values.

The real-time motion of ions is obtained by using molecular dynamics(MD)classically. The equations of motion can be obtained by variations of ionic positionRIand momentumPIobeying Newtonian equations of motion according to Ehrenfest theorem:

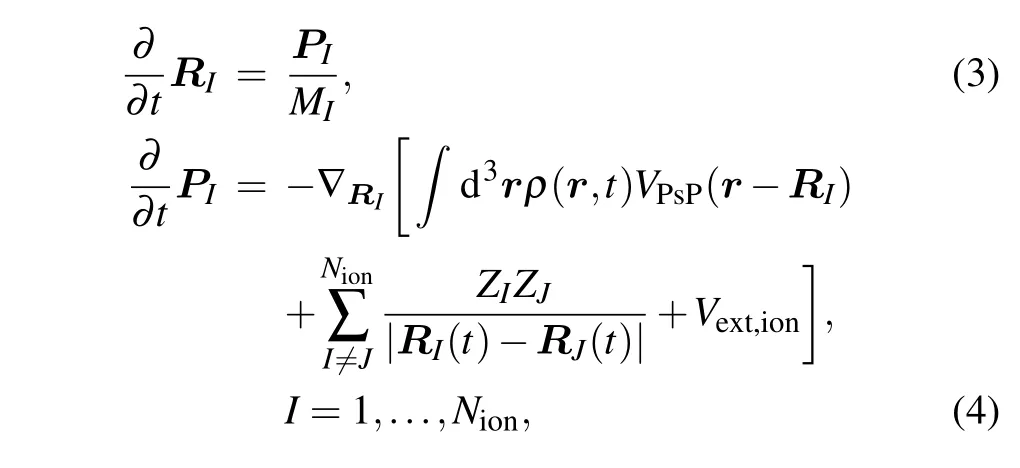
whereMIandZIstand for the mass and charge of the ion with index numberI, respectively.VPsPrepresents the pseudopotential that accounts for the coupling between ionic (RI) and electronic [ρ(r,t)] degrees of freedom, and the Goedeckertype pseudopotentials are applied.[37]Vext,ionis the interaction between ions and the external field.

In the present study,there are 42 valence electrons and 15 ions in the proton+cytosine system. All calculations are performed on a 3D coordinate-space grid of 96×96×96 with the grid spacing of 0.412a0in each direction. Firstly,the simulation is the computation of the ground state. The damped gradient method[29]and the simulated annealing method[38]are applied to obtain the ground states of wavefunction and ion,respectively. Then the dynamical Eqs. (2)–(4) for electrons and ions are computed and solved simultaneously, and both electrons and ions are fully propagated in time. A constant time step 6.05×10-4fs is applied for the propagation of the wave function and ionic motion to ensure the numerical stability.In order to avoid artificial reflections of the electronic wave functions from the boundary, a complex absorbing potential boundary[39]is applied during the collision process. The total number of electrons readsN(t)=

Vdrρ(r,t),whereVis the volume of grid space. Accordingly,the number of escaped electrons can be defined asNesc(t)=N(t=0)-N(t).

3. Results and discussion

It is well known that cytosine and guanine form the base pair CG through three hydrogen bonds in DNA. Figure 1(a)shows a CG base pair, which is connected by three hydrogen bonds indicated by dotted lines. Among these three hydrogen bonds, two hydrogen bonds, i.e., NH···O and NH···N, are formed by protons on guanine as proton donors and N and O on cytosine as proton receptors, respectively. Figure 1(b)exhibits the optimized molecular structure of cytosine with the atomic numbering shown. The optimized geometrical parameters of cytosine are the same as those in Ref.[40]. Cytosine is one of the four main bases found in DNA and RNA. It is a pyrimidine derivative, with a heterocyclic aromatic ring and two substituents attached. The plane of cytosine is in thexyplane and the center of mass is at the origin. N2 and O7 both act as the proton receptors. In order to explore the effects of N2 and O7 on the collision reaction between low-energy protons and cytosine,N2 and O7 are chosen as collision sites.Figure 1(c) displays the collision configurations. The black circles represent protons and two arrows point out the incident directions. Protons move straight towards N2(the case I)from (-1.875a0, 25a0, 0) and towards O7 (the case II) from(-0.5a0, 25a0, 0) along theyaxis. Figure 1(d) shows the contour plot of the electronic density of cytosine inxyplane indicating that ions are concentrated well around by electrons.

Fig. 1. (a) Geometry of CG base pair. The left part is guanine and the right part is cytosine. Full red, blue, grey and white circles stand for oxygen,nitrogen,carbon and hydrogen ions respectively. Hydrogen bonds are indicated by dotted lines. (b) Optimized molecular structure of cytosine with the atomic numbering shown. (c) The schematic diagrams of collision configuration for cytosine impacted by energetic proton. The cytosine is placed in the xy plane with its center of mass at the origin of the coordinate axes. N2 and O7 are chosen as collision sites respectively. The black circles represent protons and two arrows point out the incident directions. (d) The contour plot of the groundstate electronic density of cytosine in the xy plane.

3.1. Collision dynamics of proton collides with N

In this section, the detailed collision dynamics and fragmentation mechanism of cytosine impacted by proton with N2 will be discussed. To analyze the collision dynamics in detail we take the incident energy of protonEk0=900 eV as an example. Figure 2(a) shows the time evolution of ionic positions of cytosine and proton in thex-direction. As can be seen from Fig.2(a),thex-direction coordinate of proton(the violet solid line)changes at about 3.1 fs and increases at a constant rate along the negative direction of thex-axis. At the same time,thex-direction coordinate of N2(the red solid line)also changes,that is,it increases at a constant rate along the positive direction of thex-axis. This implies that proton is closest to N2 at about 3.1 fs and is rebounded. At the same time,N2 obtains a certain amount of kinetic energy and departs from the target molecule. Before the collision, the coordinates of all ions in cytosine hardly change. After the collision,all ions in cytosine show the weak vibrations except that of N2.

Figure 2(b)exhibits the time evolution of loss of electronsNescof cytosine in case I.One can find that there are two steps in the curve. The first step lasts from about 0 fs to 25 fs. In this step,no electrons lose from 0–3.1 fs,whileNescincreases rapidly from about 3.1 fs to 5.5 fs and attains about 0.76,because 0.76 electrons in cytosine are captured by proton during the closest approach and absorbed by the absorption boundary condition when proton moves to the absorption boundary.There is almost no electron loss from 5.5 fs to 25 fs. The second step occurs at about 25 fs and lasts until 45 fs, in whichNescincreases rapidly and attains about 6.2,implying that 5.44 electrons are lost. This is mainly due to the fact that N2 and its surrounding electrons move to the absorption boundary gradually,resulting in the electrons being absorbed by the absorption boundary condition. It should be noted that N2 originally has 5 outermost valence electrons. Now, when N2 leaves, it has a total of 5.44 electrons surrounded implying that N2 incidentally takes about 0.44 electrons from the remaining part of cytosine. This proves that the fragments carry away some electrons from the target molecule.

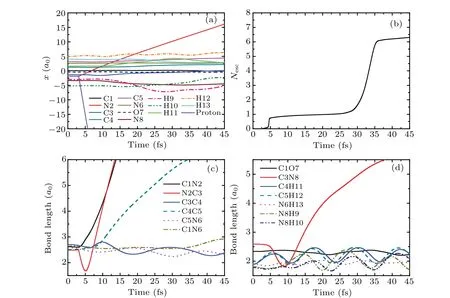
Fig.2. (a)Time evolution of ionic positions of cytosine and proton in the x-direction in case I at Ek0=900 eV.(b)The total number of escaped electrons as a function of time. (c)and(d)The variation of bond lengths of cytosine with time.

Figures 2(c) and 2(d) relate to the bonds in the ring of cytosine and the remaining bonds, respectively. As can be seen from Fig. 2(c), the bonding lengths of all bonds do not change before the collision. From 3.1 fs, the bond length of C1N2(the black solid line)increases rapidly and reaches 6a0at about 13 fs, indicating the break of C1N2 bond. However,the bond length of N2C3(the red solid line)decreases rapidly to 1.68a0at about 5 fs. After that, it increases rapidly and reaches 6a0at about 13 fs. This shows that after the collision, N2 approaches C3 first, then departs from C3 resulting in the break of N2C3 bond.For C4C5 bond,its bond length increases slowly after collision. Then,it increases rapidly from about 8 fs and reaches 6a0at about 35 fs,indicating that C4C5 bond is also broken. After the collision, the bond lengths of C3C4 (the blue solid line) and C5N6 (the pink dot line) decrease by 0.26a0and 0.13a0respectively, and vibrate regularly in the remaining time. The bond length of C1N6 (the dark yellow dash dot line)vibrates slightly before 33 fs. Then,it increases slightly and reaches 2.92a0at about 45 fs. The estimated vibration frequency of C5N6 is about 1586 cm-1,which is 7.3% higher than the calculated value 1478 cm-1of the vibration frequency of C5N6 before the collision (not shown). Thus,C5N6 bond becomes shorter after the collision,while its vibration frequency increases after obtains a certain amount of kinetic energy.This variation trend is similar to that found in Ref.[40].

It is not difficult to find in Fig. 2(d) that after the collision,the bond length of C3N8 decreases rapidly to 1.8a0,and then increases quickly. It reaches 5.5a0at about 38 fs,indicating that the C3N8 bond is also fractured. The bond lengths of C1O7 and N6H13 remain almost unchanged. The bond length of C4H11 is increased by about 0.3a0and its variation trend is consistent with that of C5H12. The bond lengths of N8H9 and N8H10 are increased by 0.16a0and 0.13a0respectively. In the whole process,all bonds vibrate slightly,except that of C3N8. The estimated vibration frequencies of C4H11 and C5H12 are both about 2650 cm-1, which are 15%lower than the experimental value 3117 cm-1.[41]The vibration frequency of N8H10 is about 2700 cm-1, which is 21% lower than the experimental value 3438 cm-1.[42]

Fig.3. The kinetic energies of proton and ions of cytosine as a function of time in case I at Ek0=900 eV.

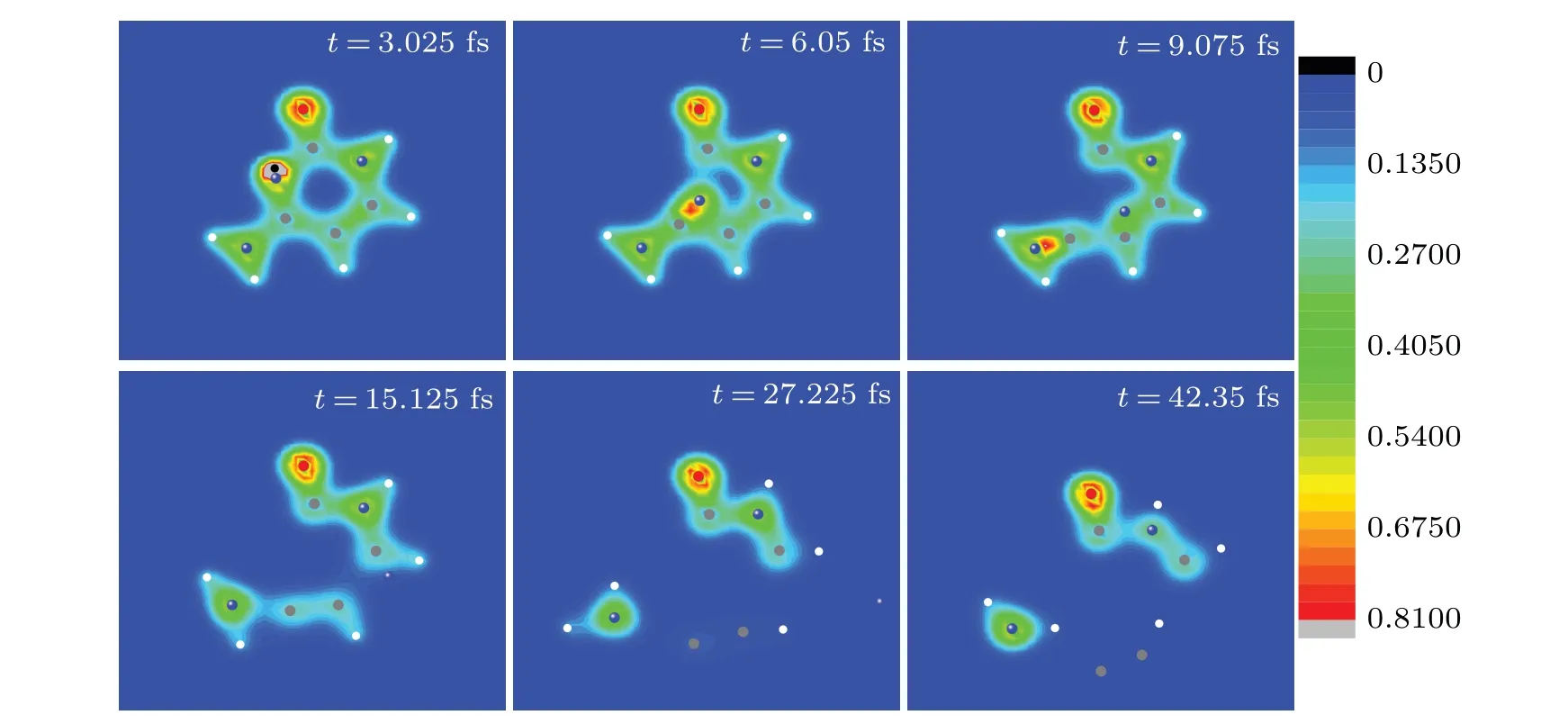
Fig.4. Six snapshots of the evolving process of cytosine impacted by proton in case I at Ek0 =900 eV.Full red,blue,grey and white circles are oxygen,nitrogen,carbon and hydrogen ions,respectively. The black circle represents the proton. The observer sees the three-dimensional snapshots from z-axis.

Figure 3(a)shows the time evolution of the kinetic energy of proton. In the whole process,the kinetic energy of proton is increased by 4 eV first,and then decreases rapidly. This is because of the medium-range polarization interaction. At about 4.8 fs,the kinetic energy of proton reaches a new stable value 772 eV, which is 128 eV lower than Ek0. Therefore, proton loses about 14.2%of the initial kinetic energy. The change of the kinetic energy of cytosine ions with time is exhibited in Fig. 3(b). Obviously, the kinetic energy of N2 (the red solid line)increases immediately to 117 eV at 3.1 fs. After that, it decreases gradually due to the medium-range polarization interaction.When N2 moves out the computational space,its kinetic energy is about 55 eV.The variation trends of the kinetic energies of C3,C4 and N8 with time are similar to that of N2.The kinetic energies of C3, C4 and N8 reach the maximum values of 18.1 eV,8.19 eV and 4.4 eV at 6.655 fs,10.59 fs and 10.89 fs,respectively,and then decrease gradually. Finally,all kinetic energies of ions are lower than 2.3 eV except that of N2.

The snapshots of time evolution of nuclear trajectories together with electronic density in Fig. 4 visualize the process discussed in Figs. 2 and 3. As can be seen from Fig. 4, proton moves along the negative direction of they-axis and approaches N2 at about 3.1 fs(see the snapshot at 3.025 fs),during which cytosine has a good electron–ion coupling without deformation. Then proton is rebounded. N2 moves towards the bond C4C5 and the bonds C1N2 and N2C3 are broken(see the snapshot at 6.05 fs and 9.075 fs). Att=15.125 fs,N2 has passed through the C4C5 bond. In the following time,N2 gradually departs from the target molecule. The C4C5 and C3N8 bonds are broken (see the snapshot at 27.225 fs and 42.35 fs). Finally,cytosine splits into four fragments,namely,N(the mass of 14),NHH(the mass of 16),CCH(the mass of 25),OCNHCH(the mass of 56). The fragments accords well with suggested ions obtained by the experimental results.[43]

3.2. Collision dynamics of proton collides with O

In this section, the detailed collision dynamics and the fragmentation mechanism of cytosine impacted by proton with O7 is discussed. In Fig. 5(a), proton (the violet solid line) is rebounded at 2.5 fs. After being impacted by proton,O7(the navy dash line)approaches C1(the black solid line)immediately. Then, C1 moves towards C4 (the dark cyan solid line)from about 3.8 fs after being attacked by O7. At about 9 fs,C1 is closest to C4. After that, H11, C4, C1 and H13 move towards the border of the computational space. O7 remains in the computing space. In addition,H9(the pink dash dot line)and H10(the olive dash dot line)move gradually to the boundary of calculation space inx-direction(not shown in Fig.5(a)).

Comparing Fig.5(b)with Fig.3(b), one can see that the curve in Fig.5(c)is more complex and has four steps.The first step occurs at about 4 fs and 0.36 electrons are absorbed. This is due to the action of the absorption boundary condition on proton and its captured electrons. From 14 fs to 30 fs,the second and the third steps appear continuously because of the absorption of electrons around H11 and C4 ions when they move to the boundary after the collision between C4 and O7. In this period, 6.58 electrons are absorbed. It should be noted that there should be 5 covalent electrons around C4 and H11.Thus,1.58 additional electrons from the target molecule are ionized.The fourth step lasts from 35 fs to 67 fs,in which about 9 electrons are lost. Among these 9 electrons, seven electrons are covalent electrons of C1,H9,H10 and H13,and two electrons are additionally ionized from the target molecule. Therefore,a total of about 3.58 electrons are ionized additionally in case II.

Fig.5. (a)Time evolution of ionic positions of cytosine and proton in the y-direction in case II at Ek0=900 eV.(b)The total number of escaped electrons as a function of time is shown. (c)and(d)The variation of bond lengths of cytosine with time.

Observing Fig. 5(c), one can find that the bond lengths of C1N2,C3C4,C4C5 and C1N6 increase immediately from about 7.5 fs and are larger than 8a0at about 30 fs indicating the breaks of these bonds. In the first 45 fs, N2C3 bond vibrates slightly with a period of about 26 fs,which is increased by 5 fs compared with the experimental value of 21 fs.[42]The bond length of N2C3 increases gradually from 45 fs and attains 7a0at 75 fs,meaning that the bond N2C3 is also broken. For the bond C5N6,it vibrates slightly in the whole time,and the vibration frequency is about 1355 cm-1.This is 8.3%lower than the calculated value of 1478 cm-1(not shown),implying that C5N6 keeps well during the collision and is less affected by the impact.

In Fig.5(d),the bond lengths of C1O7,C4H11,C3N8 and N8H9 increase rapidly from about 4.3 fs,10.7 fs and 13 fs,respectively. After experiencing the small amplitude vibrations,C5H12,N6H13 and N8H10 increase rapidly from about 45 fs.Finally,all bonds in Fig.5(d)are broken.

Figure 6 shows the kinetic energies of proton and ions of cytosine as a function of time in case II atEk0=900 eV.Because of the medium-range polarization interaction, the variation trend of the kinetic energy of proton shown in Fig.6(a)is similar to that in Fig.3(a). The proton loses about 190 eV,which is 21.1%of the incident energy. In Fig.6(b),the kinetic energies of O7, C1, C4 and H11 present a general pattern of the typical sequence of the interlaced maxima. This is due to the sequential collision and the energy transfer between them.The kinetic energies of C4 and H11 reach 104 eV and 19 eV at the moment of collision, respectively, which would lead to further collision chain reaction if there are other molecules around. The kinetic energies of remaining ions are all lower than 8 eV.

Figure 7 gives eight snapshots of the evolving process discussed in Figs.5 and 6. Att=3.025 fs,proton is rebounded capturing a certain amount of electrons from O7. Collisions between O7 and C1,C1 and C4 occur in succession and C1N2,C1N6 are broken(see the snapshots oft=6.05 fs,t=9.075 fs andt= 12.1 fs). Att= 12.1 fs, C1 has replaced C4 and C4C5 is broken. Associated with energy distribution,the dissociation pattern appears. H11 and C4 depart from the target molecule respectively (see the snapshots oft=18.15 fs andt=24.2 fs). Att=48.4 fs, C1 is approaching the border of the computational space. Finally, cytosine splits into eleven fragments(see the snapshots oft=66.55 fs,some fragments are far away from the target molecule and are out of sight),which are three carbon ions(C4,C1 and C3,each mass is 12),five hydrogen ions(each mass is 1),one nitrogen ion(N8,the mass is 14),N2O7(the mass is 30)and C5N6(the mass is 26).

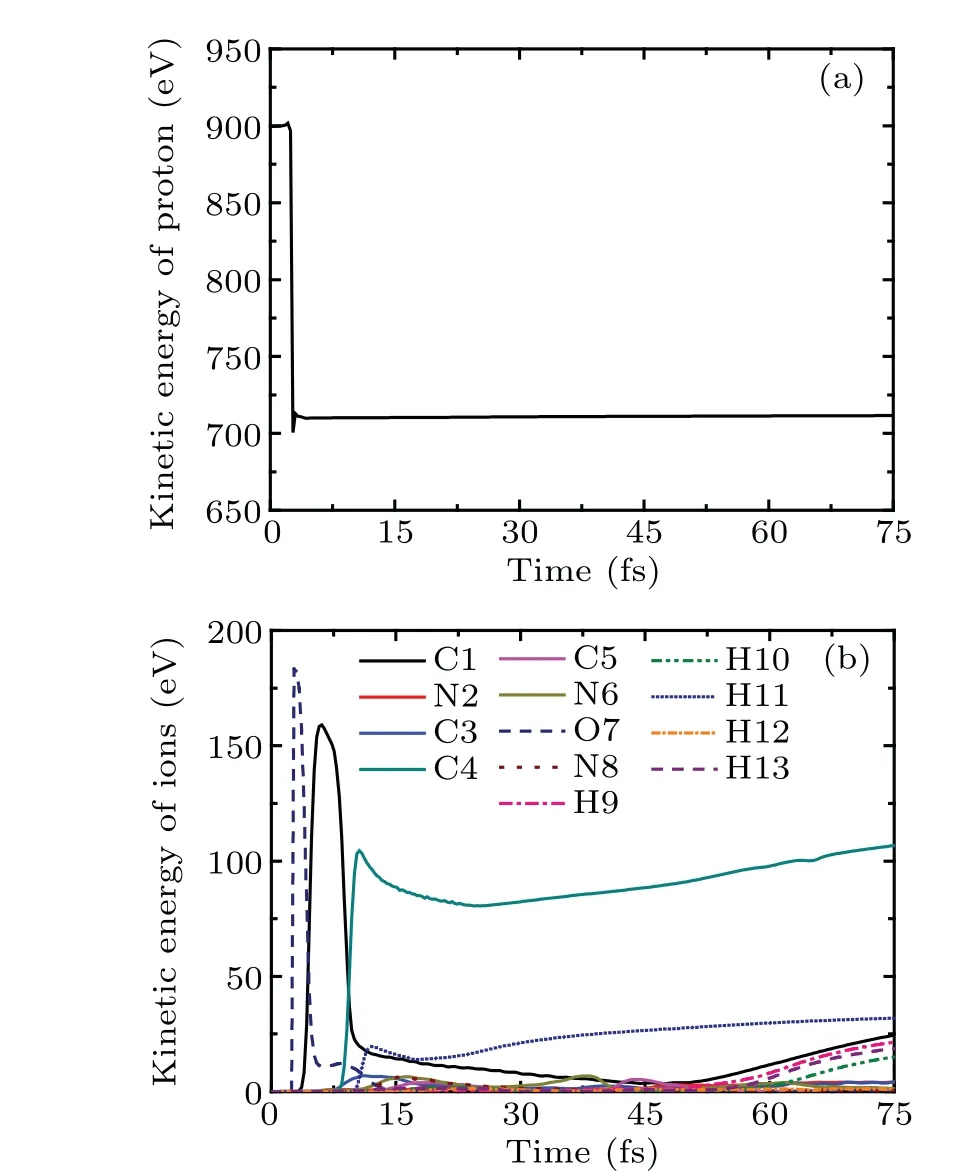
Fig.6. The kinetic energies of proton and ions of cytosine as a function of time in case II at Ek0=900 eV.

Fig.7.Eight snapshots of the evolving process of proton impacting with cytosine in case II at Ek0=900 eV.Full red,blue,grey and white circles are oxygen,nitrogen,carbon and hydrogen atoms,respectively. The black circle represents the proton. The observer sees the three-dimensional snapshots from z-axis.

3.3. Energy effect

Here, we turn to discuss the energy effect on the number of electrons captured by proton, the energy loss and the scattering angle of proton respectively. The scattering angleθis applied to describe the interaction of projectile and target.Taking into account the initial collision configurations shown in Fig.1(c),one can give the expression[26]

wherePi(i=x,y,z)are the momentum components of the outgoing proton when the simulation is over.

Figure 8(a)shows the relationship between the number of electrons captured by proton and the incident kinetic energy of proton in the two cases. It should be noted that the incident energy of proton is lower than keV,which belongs to the lowenergy region, the primary mechanism of target ionization is the electron capture according well with the results found in Ref. [22]. It can be seen that the collision site has a great influence on the number of trapped electrons. In case I (the black square line), the number of trapped electrons decreases slightly from 0.72 with the increasement ofEk0, reaching the minimum 0.67 at 400 eV,and then increases slowly,reaching 0.74 at 1000 eV. In general, the incident kinetic energy has little effect on the number of captured electrons. In case II(the red circle line),the number of trapped electrons decreases sharply with the increasement ofEk0, reaching the minimum 0.32 at 850 eV, and then increases slowly, reaching 0.35 at 1000 eV.Comparing two curves in Fig.8(a),one can find that when the incident energy of proton is the same, the number of electrons captured by proton in case I is higher than that in case II.Therefore,the electrons around N2 are more easily to be captured than those around O7. Conversely,one could predict that N2 is more likely to form hydrogen bond with proton.

Figure 8(b)gives the energy loss of proton as a function ofEk0in the two cases. The energy loss of proton increases linearly with the increasement ofEk0. In case I, proton loses about 14.2%of the incident energy,while in case II,the energy lost by proton is about 21.1% of the incident kinetic energy.Furthermore, more energy is lost when proton collides with O7(the case II)when the incident energy is the same.

Figure 8(c)exhibits the scattering angleθas a function of the incident energy of proton in the two cases. In the present study, after systematic analysis, we find that proton is scattered away in all situations. In case I, whenEk0increases,θdecrease slowly from 92.4°to 87.9°. However, it increases gradually from 139.4°to 144.6°whenEk0increases in case II.It seems that the incident energy has little effect on the scattering angle in each case. Comparing two curves in Fig.8(c), it can be found that the scattering angle is larger in case II than that in case I when proton owns the same incident energy.This implies that the collision between proton and O7 is more intense.

Fig.8. The number of electrons captured by proton(a),the energy loss of proton(b),and the scattering angle of proton(c)as a function of the incident energy of proton in the two cases.

In conclusion, it can be found from Fig. 8 that with the same incident energy, proton loses more energy and the scattering angle is larger when proton collides with O7, while it captures more electrons when colliding with N2. In addition,the incident energy of proton has a great influence on the number of electrons captured by proton,but has little influence on the scattering angle. In both cases, the energy loss of proton has a good linear relationship with the incident energy.

Figure 9 shows the mass distribution of the fragments of cytosine attacked by proton with the incident energy ranging from 150 eV to 1000 eV in the two cases. To our knowledge,only the previous cytosine fragment ion measurements available in the literature are reported for 80 keV and 100 keV proton impact[43,44]and for 12 eV and 70 eV electron impact.[45,46]According to Ref.[14],the mass of the fragments can be divided into ten categories,which are 1,12–18,25–29, 30–38, 40–43, 50–56, 67–70, 82–85, 93–98 and 111,respectively. Here,111 refers to the parent peak. It is obvious in Fig.9 that the channel of fragmentation is affected by both the collision orientation and the incident energy of proton. It should be reminded that there are two counteracting influences on the collision process.On the one hand,the faster proton exposes higher frequency components to cytosine. On the other hand, a slower proton lengthens the interaction time, which leads to an enhanced reaction yield in turn.

In case I (Fig. 9(a)), the fragment mass is 111 when 150 eV≤Ek0≤350 eV. This implies that the cytosine is not broken but deformed. The fragment masses 12–18 and 93–98 occur whenEk0=400 eV.This is due to the fact that N2 passes through the C4C5 bond and departs from the target molecule,resulting C4 and C5 are separated first and then combined together. The remaining part undergoes relaxation but does not split. WhenEk0increases from 450 eV to 1000 eV, the fragment masses are 12–18(2 counts),25–29(1 count)and 50–56(1 count), which are not affected by the incident energy. The mass of 50–56 refers to the fragment of CCNOHH, resulting from breaks of CN bond and the losses of CCH,N and NHH.In addition,no new hydrogen fragments are generated.

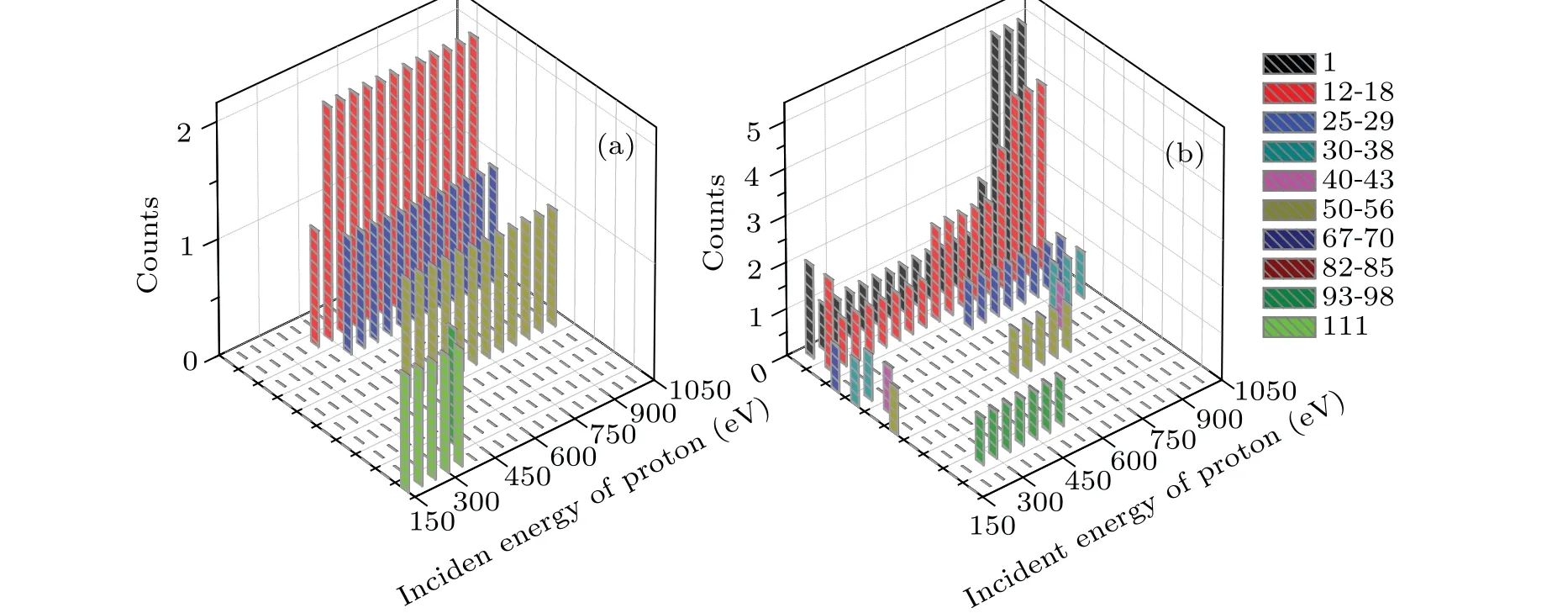
Fig.9. The mass distribution of the fragments of cytosine obtained by the impact of proton with the incident energy ranging from 150 eV to 1000 eV for(a)case I and(b)case II,respectively.

In case II (Fig. 9(b)), the mass distribution of the fragments is more sensitive to the incident energy. WhenEk0=150 eV,the fragment masses are 25–29,30–38 and 50–56,indicating that cytosine breaks into three parts. WhenEk0＞150 eV, single hydrogen ions (each mass is 1) as well as the fragment mass 12–18 appear. This means that the ring of cytosine is opened and divided. Fragments with a mass of 40–43 occur only whenEk0=200 eV andEk0=850 eV. The fragment mass of 25–29 occurs whenEk0=150 eV, 650 eV and 1000 eV. When 250 eV≤Ek0≤550 eV, the fragment mass 93–98 appears. It is obvious that the higher incident energy is associated with the higher counts observed for the fragment masses of 1 and 12–18.

3.4. Discussion about the collision site

As shown in Fig.8(a),the electrons around N2 are more easily captured by proton than those around O7. Conversely,it seems that N2 is more easily to trap proton and form the hydrogen bond. It is thus interesting to know who could capture ultra-low energy proton more easily,N2 or O7? To this end,a proton is placed to the right of O7 with the impact parameterb=0.5a0,as shown in the inset in Fig.10. The initial position of proton is (0, 13a0, 0). It moves along the negativey-axis with the incident energy of 2.5 eV to insure that it could be caught by cytosine. Figure 10 exhibits the time evolution of the relative distances between proton and O7,proton and N2.Eight snapshots of the evolving process of proton impacting with cytosine in the same case as in Fig. 10 are exhibited in Fig.11 to better show the collision process. At the initial time,the distances between proton and O7, proton and N2 are 8.3 and 12.5,respectively,as shown in Fig.10.

Fig.10.The time evolution of the relative distances between proton and O7, proton and N2. The inset shows the collision configuration. The proton moves along the negative y-axis toward O7 with Ek0 =2.5 eV and the impact parameter b=0.5a0.

Therefore, proton is closer to O7 than N2. When proton approaches O7 gradually,it also approaches N2 gradually(see the snapshot oft=12.1 fs). At about 25 fs,proton is closest to O7 for the first time,and the distance is about 1.50a0. After that,proton is closest to O7 for the second time(the distance is about 1.7a0)at about 38 fs.O7 seems to capture N2.However,the distance between O7 and proton increases gradually from about 38 fs and reaches the maximum 5.5a0at about 68 fs(see the snapshots oft=42.35 fs,t=54.45 fs andt=69.575 fs).It keeps on vibration afterwards and the average value is about 4.35a0. This is 2.518a0larger than the experimental value of the OH bond of 1.833a0,[47]implying that the OH bond is not formed, i.e., proton is not trapped by O7. For N2, at about 25 fs, proton is closest to it for the first time and the distance is about 5.06a0. After that,the distance increases first,but decreases rapidly from about 31 fs. At about 47 fs, it reaches 2.64a0. After a small swing, it reaches 1.70a0at about 62 fs.During 60 fs to 160 fs (see the snapshots oft=69.575 fs,t=99.825 fs,t=121 fs,t=139.15 fs andt=157.3 fs),the distance between N2 and proton shows a smaller and smaller vibration with time. It tends to be a stable value 1.9a0gradually. This accords well with the value 1.905a0of the bond length of N6H13 in cytosine.[48]The estimated vibration frequency is about 3250 cm-1, according well with the experimental value 3468 cm-1of the NH bond.[42]Thus, proton is trapped by N2 finally and a new NH bond is formed.

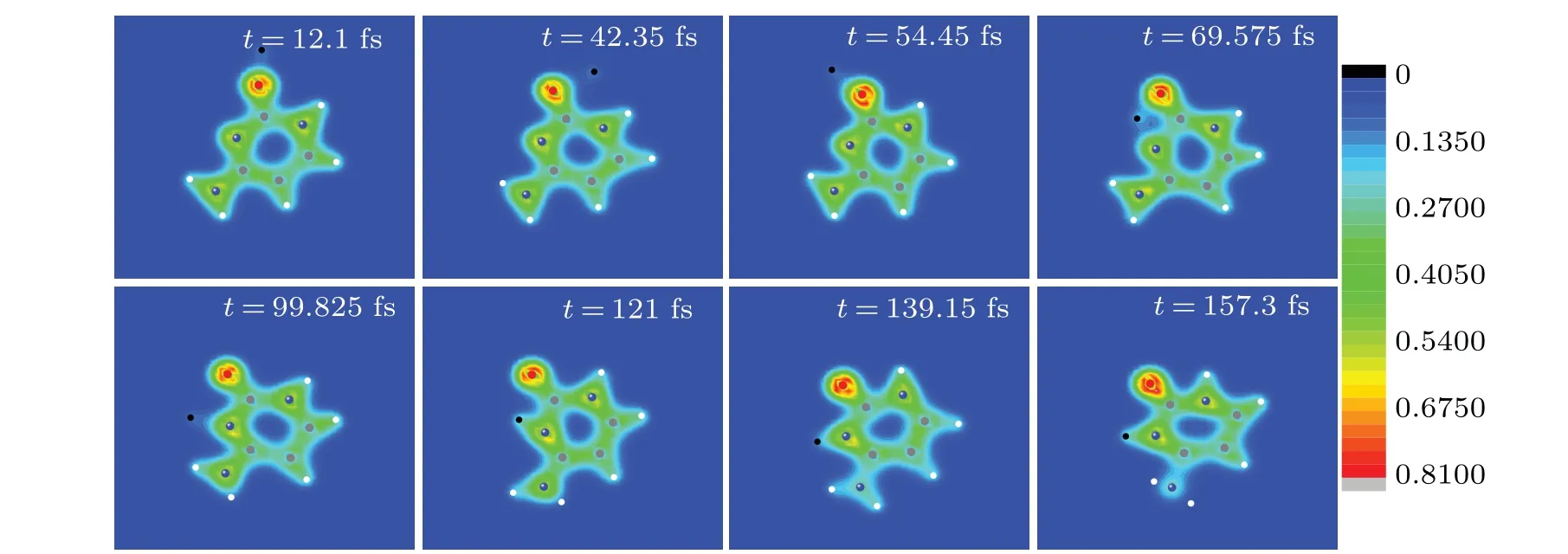
Fig. 11. Eight snapshots of the evolving process of proton impacting with cytosine in the same case as in Fig. 10. Full red, blue, grey and white circles are oxygen, nitrogen, carbon and hydrogen atoms, respectively. The black circle represents the proton. The observer sees the three-dimensional snapshots from z-axis.

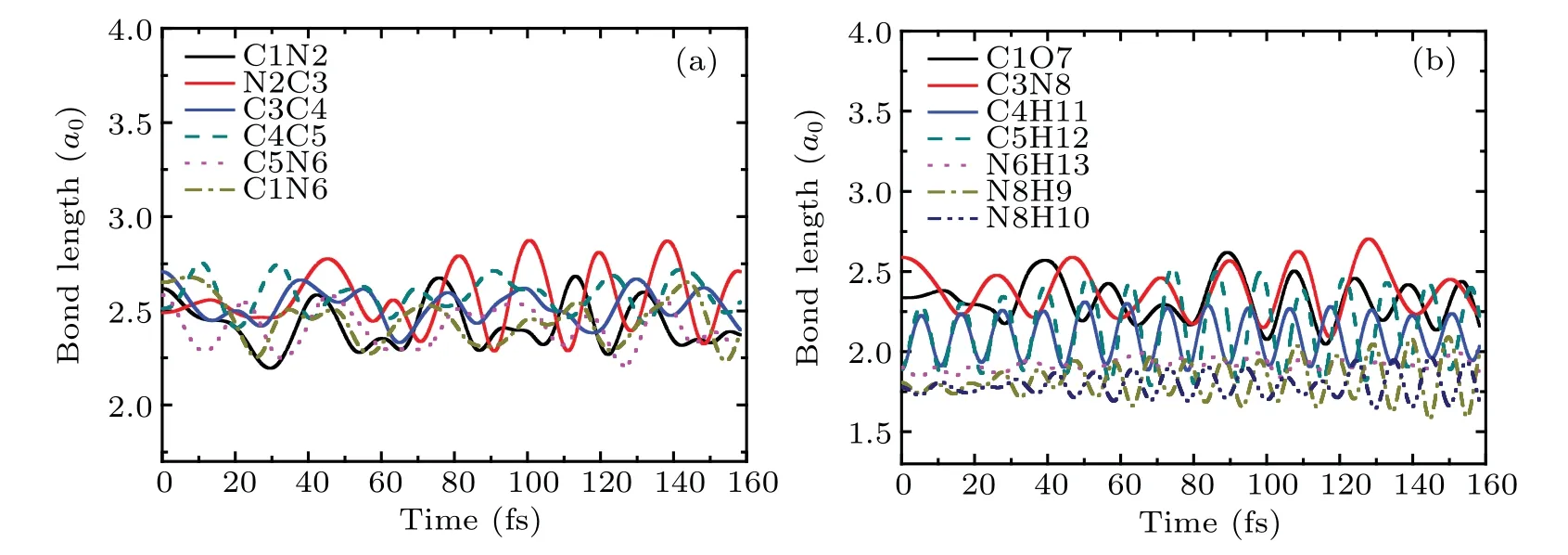
Fig.12. The bond lengths of cytosine as a function of time in the same case as in Fig.10.

The bond lengths of cytosine as a function of time in the same case as in Fig.10 are shown in Fig.12. It is obvious that all bonds of cytosine keep weak vibration and do not break throughout the whole process. Therefore, one can conclude from the estimation of bond length and vibration frequency that a new NH bond is formed.

4. Conclusion

To summary, we have theoretically explored the irradiation of cytosine by low-energy protons. Taking N2 and O7 as collision sites, we explore the effects of collision site and the incident energy of proton on collision dynamics of cytosine by quantifying the number of electrons captured by proton,the energy loss of proton, the scattering angle and the fragment mass distribution. It is found that when the collision site is N7,the number of electrons captured by proton is about 0.7,which is less affected by the incident energy of proton. The energy loss of proton is linear with the incident energy,which is 14.2%of the incident energy. With the increase ofEk0,the scattering angle of proton decreases from 92°to 88°. Cytosine does not disintegrate when 150 eV≤Ek0≤350 eV.However, whenEk0increases, after crossing the ring and C4C5 bond successively, N2 leaves the target molecule finally, resulting the appearances of the fragment masses of 12–18,25–29 and 50–56. When the collision site is O7, the number of electrons trapped by proton decreases significantly with the increase ofEk0. The energy loss of proton is 21.1% ofEk0,which is also linear withEk0. The scattering angle of proton increases slowly from 139.4°to 144.6°with the increase of the incident energy. The mass distribution of fragments of cytosine exhibits variety and is greatly affected by the incident energy due to the existence of interlocking collision reactions,that is,the collision reactions between O and C1,C1 and C4.

Through the comparison of the two collision sites, it is found that when the incident energy is the same, the scattering angle of proton is larger and the energy loss is more when proton collides with O7,resulting in more diversified mass distribution of fragments of cytosine. However, proton captures more electrons from N2,indicating that proton is easier to bind to N2. In order to further compare the binding ability of N2 and O7 to proton, a proton with 2.5 eV is launched toward cytosine much closer to O7 than to N2. The calculated result shows that proton is trapped by N2 forming a new stable NH bond finally, exhibiting that N2 on cytosine is easier to combine with low-energy protons to form NH bonds than O7.

Our calculations presented here are exploratory. They are physically motivated, time effective and shed some light on the collision site effect on the radiation dynamics of cytosine induced by slow proton. We would like to encourage experimentalists to provide data more relevant to the irradiations of nucleotides by slow protons. The cytosine explored in the present study is in the gas phase. More effort should be devoted to employing the effects of solvent and orientation on the collision process of cytosine impacted by proton. Work along that direction is in progress.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant Nos. 11905160 and 11635003), the ‘333’ Project of Jiangsu Province, China(Grant No. BRA2020327), the Science Foundation of Wuxi Institute of Technology(Grant No.ZK201903).