Hong He ,Qing Zhng ,Yru Zhng ,Jinfeng Chen ,Liqun Zhng,c,＊＊ ,Fnzhu Li,c,＊

a State Key Laboratory of Organic-Inorganic Composites,Beijing University of Chemical Technology,Beijing,100029,China

b College of Mechanical and Electrical Engineering,Beijing University of Chemical Technology,Beijing,100029,China

c Key Laboratory of Beijing City on Preparation and Processing of Novel Polymer Materials,Beijing University of Chemical Technology,Beijing,100029,China

Keywords:Rubber-like materials Hyperelastic constitutive model Strain energy function Phenomenological model Micromechanical network model UHYPER subroutine

ABSTRACT Nonlinear finite element analysis is widely used for structural optimization of the design and the reliability analysis of complex elastomeric components.However,high-precision numerical results cannot be achieved without reliable strain energy functions (SEFs) of the rubber or rubber nanocomposite material.Although hyperelastic constitutive models have been studied for nearly 80 years,selecting one that accurately describes rubber's mechanical response is still a challenge.This work reviews 85 isotropic SEFs based on both the phenomenological theory and the micromechanical network theory proposed from the 1940s to 2019.A fitting algorithm which can realize the automatic fitting optimization and determination of the parameters of all SEFs reviewed is developed.The ability of each SEF to reproduce the experimental data of both the unfilled and highly filled rubber nanocomposite is quantitatively assessed based on a new proposed evaluation index.The top 30 SEFs for the unfilled rubber and the top 14 SEFs for the highly filled rubber nanocomposite are presented in the ranking lists.Finally,some suggestions on how to select an appropriate hyperelastic constitutive model are given,and the perspective on the future progress of constitutive models is summarized.

1.Introduction

Rubber and rubber-like materials (RLMs) exhibit many unique physical and chemical properties [1,2],such as elasticity,resilience,flexibility,shock absorption,damping,sealing capability,insulation,etc.These properties of RLMs enable them to meet a wide range of requirements in industrial and engineering applications[3,4],such as tire,hose,conveyor belt,seal,damping component,artificial soft tissue,etc.The study of the stress-strain response of rubber is extremely important and an active research topic.With the fast development of computing power and non-linear numerical simulation techniques,finite element analysis (FEA) has been applied successfully to the structural optimization of the design and the reliability analysis of complex rubber components with large deformation [5–7];however,a high-precision numerical result of strain and/or stress distribution cannot be achieved without reliable hyperelastic constitutive models of the RLMs used[8].

According to search in Google Scholar,a considerable amount of scientific literature on hyperelastic constitutive models of RLMs has been steadily accumulating since the 1940s,producing over 16,000 publications,including nearly 60 papers with “hyperelastic”,“model”,and “rubber” in the title.For example,the pioneering work by Boyce and Arruda [9] focused on comparison of the accuracy of 5 hyperelastic constitutive models based on the well-known experimental data of Treloar [10] under three deformation modes,i.e.,uniaxial tension (UT),pure shear(PS),and equibiaxial tension(ET).Attard and Hunt[11]then verified the validity of their rubber constitutive model with the different types of experimental data of UT,ET,planar tension(PT),biaxial tension(BT)and uniaxial compression(UC).Hoss and Marczak[12,13]classified and sorted 40 strain energy functions (SEFs) based on strain invariants proposed from the year 1944–2010.They found that the models including theterm could represent the softening characteristic at small strain while the models containing the lnI2term could easily capture the stress hardening at high strain.Another outstanding work was done by Marckmann and Verron [14].They compared 20 different hyperelastic constitutive models,ranking them by their ability to reproduce the experimental data.Steinmann and Hossain [15,16] systematically reviewed 25 hyperelastic constitutive models and found that it was difficult to reliably predict the mechanical behavior of RLMs under all

deformation modes when only one type of test data was provided.Horgan and Saccomandi [17–19] introduced the theory of limiting chain extensibility in detail and reviewed the related hyperelastic constitutive models of rubber-like and biological materials.Martins et al.[20] evaluated the accuracy of 7 hyperelastic constitutive models to study the nonlinear mechanical response of soft tissue and silicone rubber via correlations between experimental and theoretical data.Beda [21]summarized 29 phenomenological hyperelastic constitutive models of RLMs and explained the derivation process of some classical constitutive models such as the Takamizawa-Hayashi model,the Hart-Smith model,the Gent model,and the Beda model.Dal et al.[22] reviewed the reproducibility of experimental data according to 40 hyperelastic constitutive models using the multi-objective optimization parameter identification toolbox.Ding et al.[23]showed the derivation relations of 31 hyperelastic constitutive models including phenomenological models and statistical mechanics models.In addition,the similarity and quantitative equivalence of different models were given using the coefficient of determination and the Fr′echet distance between models.

Although hyperelastic constitutive models of RLMs have been studied for nearly 80 years,how to construct and select a reasonable constitutive model to accurately describe the mechanical response of rubber is still one of the major active research fields of RLMs.The sea of scientific papers and the constantly evolving constitutive models make it challenging for researchers and engineers to select the most reliable hyperelastic constitutive model from among all the models existing.

To gain a clearer picture,this article is organized as follows:This work first comprehensively reviews 85 isotropic hyperelastic SEFs based on both the phenomenological theory and the micromechanical network theory proposed from the 1940s to the year 2019.Then a fitting algorithm using the nonlinear least square optimization method is developed that can simultaneously realize the automatic fitting optimization and parameters determination of all the hyperelastic SEFs.The ability of each SEF to reproduce the experimental data of both the unfilled and highly filled rubber materials is quantitatively assessed based on a new proposed evaluation index.The top 30 SEFs for the unfilled rubber and the top 14 SEFs for the highly filled rubber materials are presented in the ranking lists.We also list the suggested value regions of the material parameters for all the micromechanical network models and part of the phenomenological models based on the literature survey and our fitting results.Finally,some suggestions are given on how to select an appropriate isotropic hyperelastic constitutive model of RLMs,and the perspective on the progress of constitutive models of RLMs is summarized.

2.Some basic concepts of hyperelastic constitutive models

Before the review work,we simply introduce some basic concepts of hyperelastic constitutive models.Different from the microstructure of metal,ceramic,or plastic,the very flexible and long macromolecular chains together with crosslinking and entangled macromolecular network render rubber a special mechanical response;for example,it can deform nonlinearly with large deformation,and it can almost completely recover its original configuration when the external force is removed[24,25].Due to the strong geometrical and physical nonlinearity and the nearly incompressible nature of rubber,the constitutive models of rubber materials are generally represented by a strain energy function (W)rather than a direct stress-strain relation.The complex and highly non-linear behavior of rubber is generally studied from the following five main aspects [26]:(i) the hyperelastic behavior under static or quasi-static load,(ii)the viscoelastic behavior under cyclic loadings such as hysteresis [27] and the Payne effect [28–30],(iii) the permanent set and stress-softening phenomenon also called the Mullins effect undercyclic loadings [31–33],(iv) the orthotropic or even anisotropic mechanical response[34,35],and(v)damage,failure,and aging[36–38].

In this work,the RLMs are considered to be homogeneous,isotropic,incompressible or nearly incompressible,and all inelastic phenomena such as permanent set,hysteresis,Payne effect,Mullins effect or damage are tacitly ignored.We only focus on the isotropic hyperelastic response of RLMs under the static or quasi-static load.

Based on the continuum mechanics method [39,40],for homogeneous,isotropic,and incompressible or nearly incompressible rubber,the SEF can be written in a polynomial form composed of strain invariants(or expressed in the form of a stretch ratio).The three strain invariants of the right Cauchy-Green deformation tensor are as follows:

whereIis the strain invariant and λ is the stretch ratio.The subscripts 1,2,and 3 stand for the three principal directions.

For the nearly incompressible rubber,the SEF can be expressed as the sum of the deviatoric hyperelasticity (WDev) for shape change and the dilatational hyperelasticity(WDil)for volume change,shown in Eq.(4).

For incompressible rubber,the SEF can be expressed only as deviatoric hyperelasticity without dilatational hyperelasticity.This means the third strain invariantI3equals one.

This work focuses on the deviatoric strain energy functionWDevof incompressible RLMs.

3.Review of hyperelastic constitutive models of RLMs

The SEFs of RLMs can be roughly divided into two main categories:phenomenological models based on continuum mechanics and micromechanical network models based on microstructure.The 85 SEFs of RLMs we review are shown in Fig.1.The detailed introduction of the model classification is shown in a later section.

Fig.1.The classification of 85 hyperelastic SEFs for RLMs.

3.1.Phenomenological models

Phenomenological models are based on the fitting of experimental data of mechanical response via mathematical equations,and,in most cases,the material parameters do not have physical meanings [45].As mentioned earlier,the phenomenological model can be expressed by the combination of the strain invariants and/or stretch ratio.Such models can be further divided into phenomenological models based on strain invariants,phenomenological models based on stretch ratio,and mixed phenomenological models based on both strain invariants and stretch ratio.

3.1.1.Phenomenological models based on strain invariants

The phenomenological models based on strain invariants can be further divided into three types:(1) series function models;(2) power law,exponential or logarithmic function models;and (3) limiting chain extensibility models.

(1) Series function models

The most general series expansion of SEF based on strain invariants was proposed by Rivlin[46,47].

whereCijare the material parameters.Ifi=1 andj=0,the simplest and widely used Neo-Hookean model[48]can be obtained.

If only the first two terms in Eq.(6)are retained,the Mooney-Rivlin model[47]can be obtained.

whereC10andC01are material parameters.The Mooney-Rivlin model has been widely used in the analysis of rubber components with medium deformation.According to Tschoegl [50],the main shortcoming of the Mooney-Rivlin model is that not enough expansion terms are retained based on the Rivlin polynomial series.Many other researchers have proposed high-ordered series function models based on the form of the Rivlin model.In general,the high-ordered series function models based on the Rivlin give people the impression that their fitting accuracy is much higher and the scope of application is wider for these models.However,we think specific analysis is required for some special rubber materials,which will be discussed later.A full list of the model name,the year,the strain energy function,the number of material parametersinvolved,the material parameter symbols and the original reference for each series function model is presented in Table 1.

Table 1 14 phenomenological models in the form of the series function based on invariants (Params represents the number of material parameters).

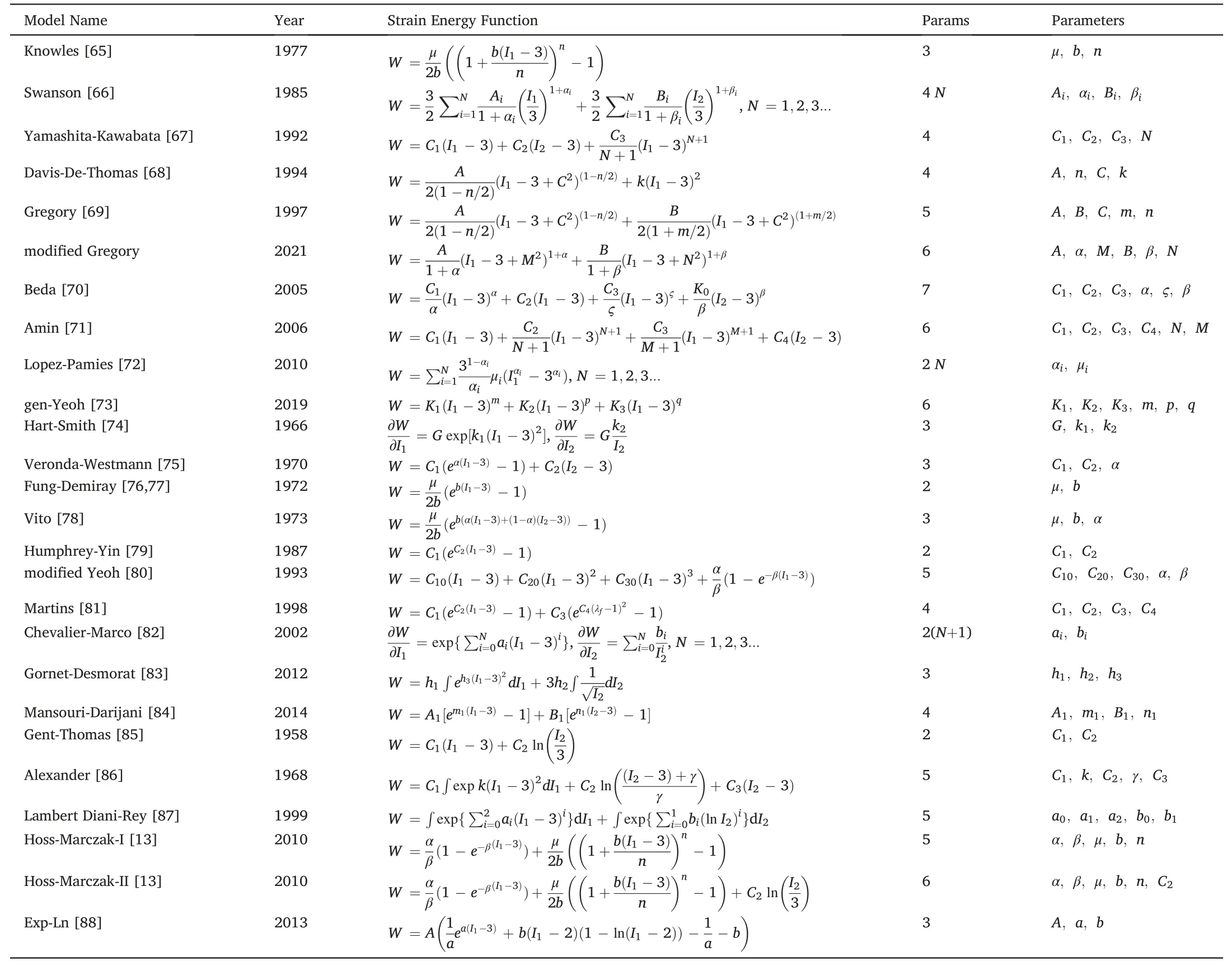
Table 2 26 phenomenological models in the form of the power law,exponential or logarithmic functions based on invariants.

Table 3 11 phenomenological models considering the limiting chain extensibility based on invariants.

Table 4 6 phenomenological models based on stretch ratio.

Table 5 Mixed phenomenological models.

Table 6 Gaussian chain network models.

Table 7 Non-Gaussian chain network models.

Table 8 Mixed micromechanical network models.

(2) Power law,exponential or logarithmic function models

Previous studies showed that most rubber materials soften under small deformation but rapidly stiffen as the strain increases.However many classical SEFs failed to reproduce such mechanical responses under all deformation modes[63,64].For this reason,power law,exponential and logarithmic functions were introduced to achieve a good prediction of the mechanical behavior of RLMs.Similar to Table 1,such SEFs are listed in Table 2.Specifically,inspired by the Gregory model [69],we propose a modified Gregory model.The expression of the modified Gregory model is shown in Table 2.Gregory introduced the concept of variable power to improve the flexibility of the fit.The strain invariants(I1-3) from the former and latter items in the Gregory model share the same material parameterC.We changed the material parameterCinto two different material parametersMandN.The newly proposed modified Gregory model is also a phenomenological model and contains six material parameters(A,B,M,N,α,and β).

(3) Limiting chain extensibility models

Yeoh[55]modified the SEF by using high-orderedI1terms in order to improve the fitting precision of the model for a wide range of strains.After the high-ordered term was introduced,the model fitting results were in good agreement with the test data under the condition of large strains.In addition,the model parameters determined by UT test data were suitable for other deformation modes (e.g.PT,ET).However,the Yeoh model was not accurate at small deformation.Gent[89]solved the problem by introducing the concept of the stretch ratio limit of the macromolecular chain of rubber.He believed that there was a maximum valueIm;then he proposed the following famous SEF.

whereEandImare material parameters.Eis the tensile modulus at small strains.The Gent model can be equivalent to the Neo-Hookean model whenImtends to infinity.Other models related to the limited extensibility of macromolecular chains are introduced in Table 3.

3.1.2.Phenomenological models based on the stretch ratio

Valanis and Landel [102] proposed a simple phenomenological SEF based on the stretch ratio for incompressible rubber materials,shown in Eq.(10).

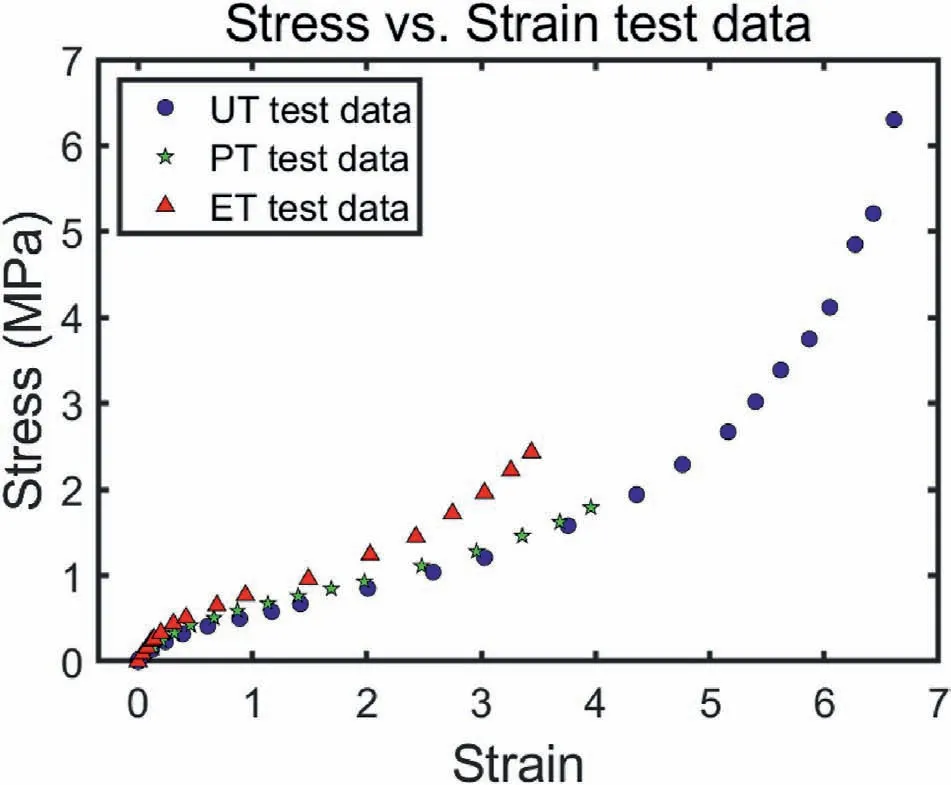
Fig.2.The Treloar's test data (UT,PT and ET) for unfilled rubber.Replotted from Ref.[10].

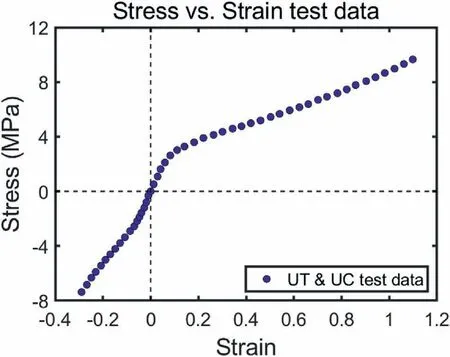
Fig.3.The test data (UT and UC) of a highly filled hydrogenated nitrilebutadiene rubber (HNBR) compound for a typical packer seal.Replotted from Ref.[73].

where μ is a material parameter.Based on the hypothesis proposed by Valanis and Landel,Peng and Landel [103] obtained a SEF in the following form.

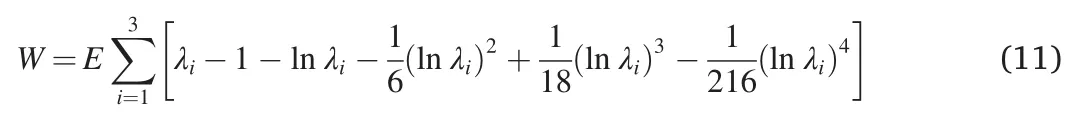
whereEis a material parameter.To reduce the complexity of using invariants to describe the SEF,Ogden [104] ignored the assumption that the SEF was an even function of the principal stretch ratio and proposed a new SEF,shown in Eq.(12).

where αn,βnare material parameters.Rivlin,Sawyers[105]and Treloar[25]pointed out that the Ogden model was a special equivalent form of the Mooney-Rivlin model.The Ogden model can be utilized in a wide strain range with great flexibility.Other typical phenomenological models based on the stretch ratio are shown in Table 4.

3.1.3.Mixed phenomenological models

The phenomenological SEF expressed in terms of both strain invariants and stretch ratio is called the mixed phenomenological model in our work.Most of the SEFs are not applicable to the loading conditions of both small deformation and large deformation;therefore,the emergence of mixed SEFs is a good solution.Not only can the mixed models ensure the accuracy of the simulation,but they also take into account the respective characteristics of the two SEFs.Typical mixed phenomenological models include the continuum hybrid model proposed by Beda and Chevalier[108],the Bechir-4term model[109]and the WFB model[110].Mixed phenomenological models are shown in Table 5.

3.2.Micromechanical network models

Micromechanical network models are based on the physical and statistical methods of polymer chain networks and material microstructure.Different from the parameters in phenomenological models,the material parameters of micromechanical network models do have physical interpretations.So they are superior to the purely phenomenological models when the models are adopted to explain the relations between microstructures and properties of RLMs.According to the statistical characteristics of macromolecular chains,micromechanical network models can be divided into three types:Gaussian chain network models,non-Gaussian chain network models and mixed micromechanical network models.

3.2.1.Gaussian chain network models

Kuhn[111,112]first proposed the use of statistical theory to calculate the conformation of the polymer chain.He considered that the probability density function of the end distance of the polymer chain in small deformation and the free state is a Gaussian function.Treloar [113]applied Gaussian statistical theory to the molecular chain network to describe the macroscopic behavior of RLMs and obtained the SEF shown in Eq.(13).

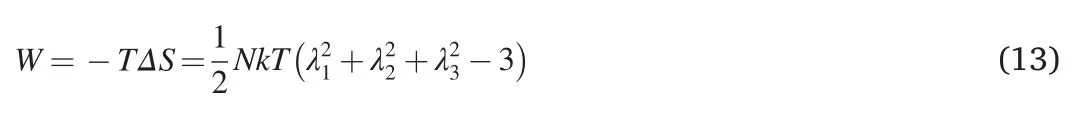
ΔSrepresents the change in conformational entropy of the molecular chain per unit volume,Nis the number of network chains in the crosslinked network per unit volume,Tis the thermodynamic temperature,kis the Boltzmann's constant,NkTrepresents the initial shear modulus.The Gaussian model is based on the assumption that the end distance is much smaller than the total length of the chain.It can only be used to approximate the situation of small deformation.The Gaussian model is equivalent to the Neo-Hookean phenomenological model,and it assumes that the ideal polymer network is composed of chains that freely pass through each other without considering the intermolecular forces.However,in real macromolecular networks,the polymer networks have topological constraints due to the formation of entangled and crosslinked states.A series of micromechanical models based on Gaussian chain distribution,shown in Table 6,was developed after considering such effects.These models can only describe the stress-strain responses from small to moderate deformations and fail to describe stress hardening under large deformation.

3.2.2.Non-Gaussian chain network models

When the end distance of the molecular chain reaches 40% of the fully extended length,the influence of non-Gaussian chains should be considered.Therefore,to improve the accuracy and applicability of the models,a new model considering the non-Gaussian statistical characteristics of molecular chains is needed.

Kuhn and Grǜn[127]used Langevin statistical theory to explain the effect of molecular chain elongation based on the random walk statistical theory of the ideal affine chain.The non-Gaussian chain network models are obtained by applying the mechanical property of the non-Gaussian single chain to the molecular chains of the rubber network.The earliest non-Gaussian chain network model is the three-chain model[117].This model assumed that the molecular chains of the network were distributed along three principal directions,and the molecular chains would show affine deformation with the deformation of the rubber materials (affine hypothesis).Later,Flory [128] proposed the four-chain network model based on the three-chain network model,which assumed that four molecular chains were connected to the center by the four vertices of a tetrahedron.The three-chain network model and the four-chain network model can describe stress-strain behavior under a certain deformation mode (e.g.UT) well,but they can't predict the mechanical behavior of rubber materials under multiple deformation modes simultaneously.Based on this,Arruda and Boyce [129] proposed the Arruda-Boyce model to capture the hardening behavior of the rubber materials by considering the limited chain extensibility of a single chain.

After the introduction of the effect of chain entanglement and crosslinking into non-Gaussian theory,a series of non-Gaussian chain models appeared,shown in Table 7.

3.2.3.Mixed micromechanical network models

Due to the defects of Gaussian chain network models and non-Gaussian chain network models,some researchers paid attention to the mixed micromechanical models.Wu and Van der Giessen [139–141]combined the three-chain model and the Arruda-Boyce model by a constant or a physical quantity related to the deformation process.Eli-as-Zuniga and Beatty [142] proposed a combination model of the three-chain model and the Arruda-Boyce model,to replace the full network model.Lim [143] proposed a mixed model based on the Gaussian chain network model and the Arruda-Boyce model in his work,that is,the Gaussian chain network model is adopted when the length of the molecular chain end vector isr＜0.8Nl,while the Arruda-Boyce model is adopted when 0.8Nl ＜r＜Nl.Bechir et al.[144] considered the influence of the interaction between the chains of the cross-linked network into a mixed model.The free energy function of the constraint network is simply processed using the three-chain model,and that of the unconstrained network is constructed utilizing the Arruda-Boyce model.See Table 8 for the mixed micromechanical network models.

The phenomenological constitutive models based on continuum mechanics can describe the stress-strain response of material under a wide deformation range.But they could not provide an understanding of the nature of the molecular structure,and these models may produce unrealistic results beyond the deformation mode and strain range determined by the fitting parameters of the material.The micromechanical network model based on microstructure is suitable for the establishment of a correlation between the microstructure of the material and the mechanical properties.The parameters in the micromechanical network model have real physical meanings,so more and more attention has been paid to the physically-based model by the research community.On the other hand,with the increasing needs of FEA in the design and optimization of rubber products,in-depth study of constitutive models for rubber is essential to improve the accuracy of the FEA.

Tables 1–8 give full lists of the model name,the year,the strain energy function,the number of material parameters involved and material parameter symbols.We didn't list the physical meanings of the material parameters involved one by one in the tables.But we gave the original reference of each model.There is a clear description of each material parameter for every model.For the known regions of the material parameters involved,we listed the suggested value regions for the material parameters of all the micromechanical network models.Due to the unclear physical meaning of the material parameters of the phenomenological model,the acquisition of such parameters mainly depends on the fitting optimization algorithm.Similarly,based on the literature survey and some calculation results,the suggested value regions of the material parameters of some phenomenological models are also given.See Table S1 for details.

Table 9 The computational time and Mises stress distribution of the dumbbell rubber specimen under uniaxial tensile loading for the cases using the Lambert Diani-Rey model,the Alexander model and the Gornet-Desmorat model implemented with user-defined material subroutines in Abaqus/Standard (UHYPER).

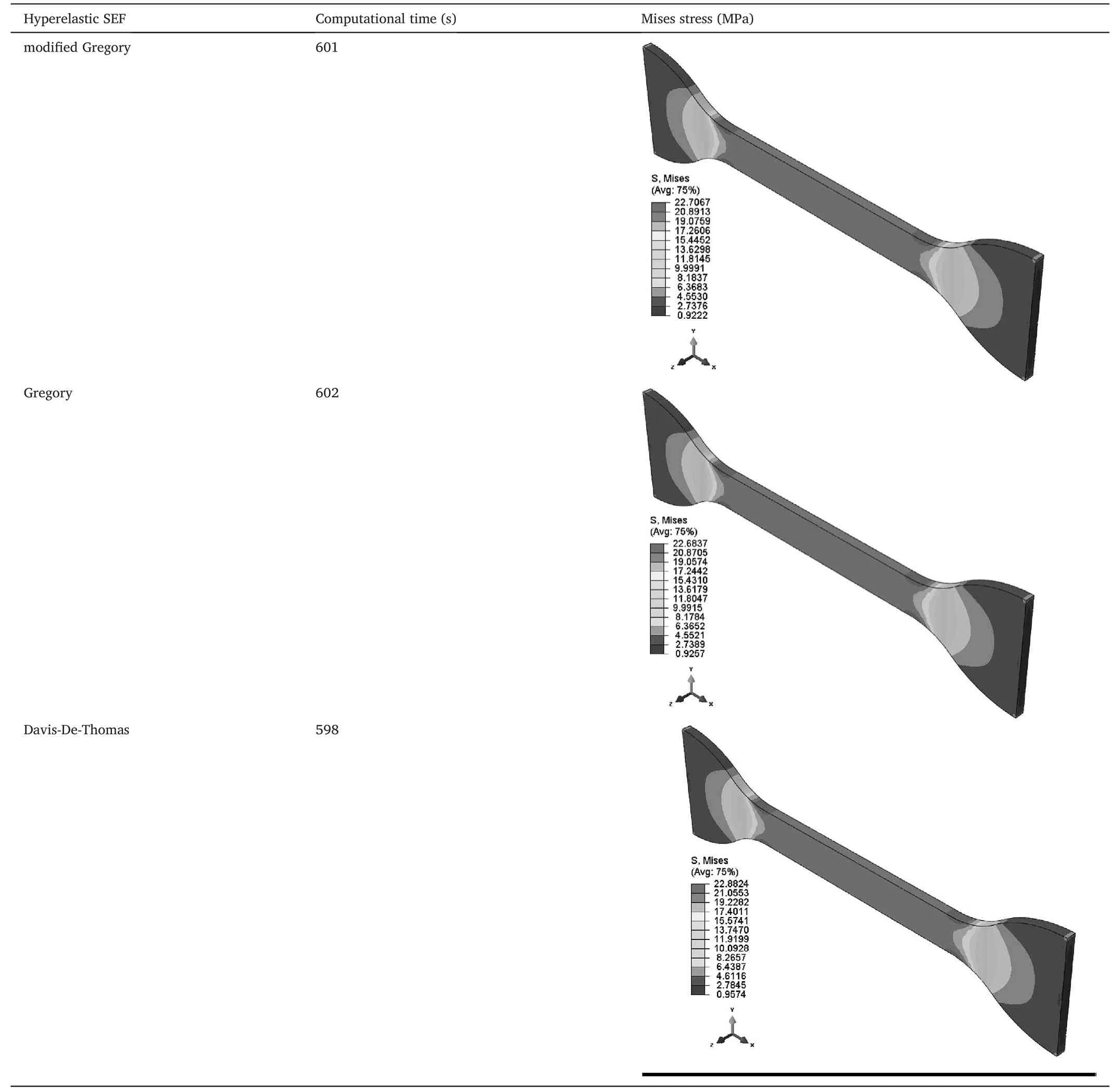
Table 10 The computational time and Mises stress distribution of the dumbbell rubber specimen under uniaxial tensile loading for the cases using the modified Gregory model,the Gregory model and the Davis-De-Thomas model implemented with user-defined material subroutines in Abaqus/Standard(UHYPER).

The SEFs of RLMs have been studied for nearly 80 years.In the above section,we comprehensively reviewed 85 hyperelastic SEFs of RLMs based on phenomenological theory and micromechanical network theory proposed from the 1940s to the year 2019.Although many pioneering studies have been done to assess the pros and cons of various SEFs,especially on the description of unfilled rubber,it is still a burdensome endeavor to select an appropriate SEF for the RLM at hand.In the following,we carry out the work on how to evaluate the SEFs and select the proper one or ones.

4.Determination and evaluation of SEFs for RLMs

The determination and evaluation of hyperelastic constitutive models are mainly based on the fitting precision that a specific SEF can realize in reproducing the mechanical response of RLMs.In general,an ideal SEF should(1)contain as few material parameters as possible;(2)accurately reproduce a complex mechanical response under multiple deformation modes and a wide range of strains;(3) contain the material parameters that do have physical meanings;(4) satisfy the requirement of Drucker stability [145,146];(5) take less computational time when used in the engineering application.

Some outstanding works have been done in this field.Marckmann and Verron [14] analyzed 20 different models and ranked them for the Treloar's data.The results showed that the extended-tube model,the micro-sphere model,the Shariff model and the Ogden model provide the best results.Dal et al.[22] gave a ranking list of models based on two groups of experimental data reported by Treloar and Kawabata et al.[147].The top five models were the micro-sphere model,the Alexander model,the Lambert-Diani-Rey model,the extended-tube model,and the Shariff model.However,considering that the material parameters should have physical significance,they believed that models with tube constraints such as the micro-sphere model and the extended-tube model are better than the models without tube constraints.Seibert and Schüche[148] compared the prediction ability of six different models using the UT and ET test data of carbon black filled rubber,and concluded that the high-ordered term was very important to reproduce the typical stress stiffening characteristics under large deformation.Considering their experimental data,they found that the Van der Waal model,the Arruda-Boyce model and the Yeoh model could reliably predict equibiaxial tensile response when only the UT test data was provided.Steinmann and Hossain [15,16] derived accurate stress tensors and tangent operators from different phenomenological and micromechanical network models,and they revealed the abilities of 25 SEFs to predict the mechanical response under other deformation modes when only one kind of experimental data (e.g.UT,PT or ET) was provided.Because of the shortcomings of the Arruda-Boyce model,which was known to be significantly deficient in predicting the ET response,Hossain et al.[149] compared 5 modified versions of the Arruda-Boyce model and two modified versions of the full network model with the classic Arruda-Boyce model.He concluded that the Gornet-Desmorat model,the modified Flory-Erman model,the bootstrapped-8-chain model and the Meissner-Matˇejka model could predict the stress-strain response under all three deformation modes better than the Arruda-Boyce model.Horgan et al.[150] compared the fitting quality of the Vito model and the Fung-Demiray model for the experimental data under different deformation modes,and concluded that the SEF with the second strain invariant of the right Cauchy-Green deformation tensor could more accurately describe the mechanical response of RLMs.Fujikawa et al.[151] used the experimental data of UT,PS and BT of vulcanized styrene-butadiene rubber with different carbon black content to evaluate the Arman-Narooei model,the SpT model,the Exp-Ln model,and the Mansouri-Darijani model,and they found that the SEF with the first strain invariant of the right Cauchy-Green deformation tensor had good repeatability and predictability for the RLMs studied.

Many pioneering works have been done on the identification of the parameters of hyperelastic constitutive models of RLMs.These works laid the in-depth foundation of the research in this field.Benjeddou et al.[152],N¨orenberg and Mahnken [153],Ogden et al.[154],and Twizell and Ogden[155]utilized a non-linear least squares optimization method to estimate the material parameters of the Ogden model.The main difficulty in the parameter identification process is to determine appropriate initial values.Dal et al.[156] developed a multi-objective optimization method together with a MATLAB genetic algorithm to identify the parameters of 10 SEFs,and obtained the accurate material parameters for each model.Yevgen et al.[157] developed a program based on computer-aided engineering to identify and verify the material parameters of 9 SEFs by fitting the Treloar's data.

In addition,with the increasing need for a high quality hyperelastic constitutive model,lots of fitting tools appeared.For example,the commercial finite element software ABAQUS provides 17 SEFs in six categories for the fitting operation.The users can also write UHYPER or UMAT subroutines to define a specific hyperelastic constitutive model according to their own design needs.Another commercial finite element software,ANSYS,can also perform the parameter-fitting calculations of the hyperelastic constitutive models.Hyperfit [158] is a famous fitting software for hyperelastic and/or viscoelastic constitutive models.Material parameters can be identified from the user's test data.It provides a large number of isotropic/anisotropic,compressible/incompressible SEFs to be calibrated for FEA.In addition,MCalibration [159] is a powerful calibration tool,which can extract the material parameters for all SEFs in ABAQUS and ANSYS.Plagge developed an on-line platform for the fitting of hyperelastic constitutive models for RLMs.The platform is convenient and easy to use.Users can also customize their own proposed or modified SEFs[160].

However,we need to mention two points here in particular.Firstly,the hyperelastic SEFs studied by all the previous pioneering work are up to around 40 types,that we know of.None of these completed works fully demonstrate the fitting effects of the 85 hyperelastic SEFs we reviewed above.Secondly,many reported works focused on the experimental data of unfilled rubber;for example,the classical Treloar's data.Some work[161,162]concluded that the work on unfilled rubber would be significant for filled rubber because the shape of the stress-strain curves with different filler contents are similar;however,this may be not true for some highly filled rubber materials.

In this work,we selected the experimental data of two hugely different rubber materials -the Treloar's data (UT,PT and ET) [10] for unfilled rubber,shown in Fig.2,and the test data(UT and UC)[73]for a highly filled hydrogenated nitrile-butadiene rubber (HNBR) compound,shown in Fig.3,for a typical packer seal to compare the reproducibility of each SEF.The stress-strain responses of the Treloar's data mainly show that the stiffness decreases at small strains,then a linear interval with almost constant stiffness appears at medium strains,and finally the stiffness increases at large strains.This phenomenon is due to the combined effect of the limited extensibility of macromolecular chains and strain-induced crystallization [25].The stress-strain curve of the highly filled HNBR is very different from that of unfilled rubber.Due to the Payne effect,the filler network is destroyed at low strains and the stiffness decreases rapidly.The UT and UC stress-strain curves show more prominent nonlinear characteristics.

The nonlinear least square optimization method based on the lsqcurvefit tool from MATLAB software was adopted.We developed an algorithm program that can realize the automatic fitting optimization and parameters determination of 85 SEFs in turn.The core of this algorithm program is the simultaneous fit of the specific experimental data by using the derived nominal stress vs.nominal strain expression from each corresponding SEF under every deformation mode provided from the test.The criterion for the end of the fitting operation is that the coefficient of determination (R2) reaches the maximum value.The derived nominal stress vs.nominal strain (or stretch ratio) expressions for each corresponding SEF under all deformation modes are given below.To describe the large deformation of the RLMs,two types of stresses are classically defined:the true(or Cauchy)stress σ and the engineering(or nominal)stressP.

In the formula,prepresents the hydrostatic pressure.Using the above formula,the stress-stretch expressions under every simple deformation mode(UT,PT and ET)can be derived.

For the deformation mode of uniaxial tension:

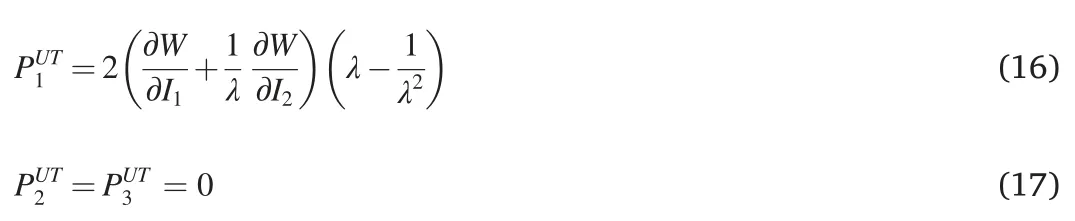
For the deformation mode of planar tension:

For the deformation mode of equibiaxial tension:

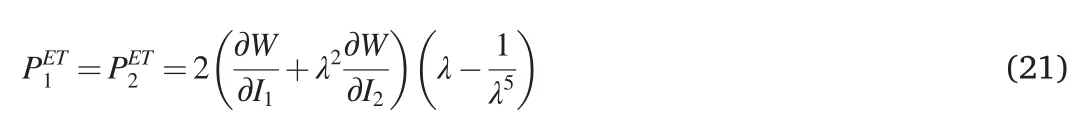
where the subscripts 1,2,and 3 stand for the three principal stretch directions.

To compare the fitting accuracy of each SEF,the coefficient of determination,R2,is defined by Eq.(23).

In Eq.(23),n is the total number of measurement points.is the test data of the engineering stress at specific stretchis the fitting data of the engineering stress corresponding to specific engineering strainis the mean value of the engineering stress for all the measurement points.

The top 10 hyperelastic SEFs used to fit the Treloar's data are shown in Fig.4.The coefficient of determination (R2) and the number of parameters(Params)are shown at the bottom right of the figure.The scatter data represent the test data and the lines stand for the fitting data by the specific SEF.The name of each model is shown at the top of the figure.The abbreviation “Ni” means the model isi-ordered.For example,Swanson N2 model and Swanson N3 model are the second-ordered and the third-ordered Swanson model,respectively.

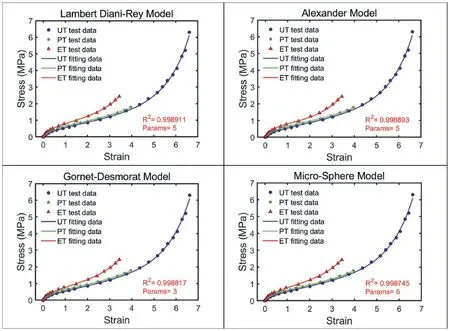
Fig.4.The top 10 SEFs used to fit the Treloar's data.

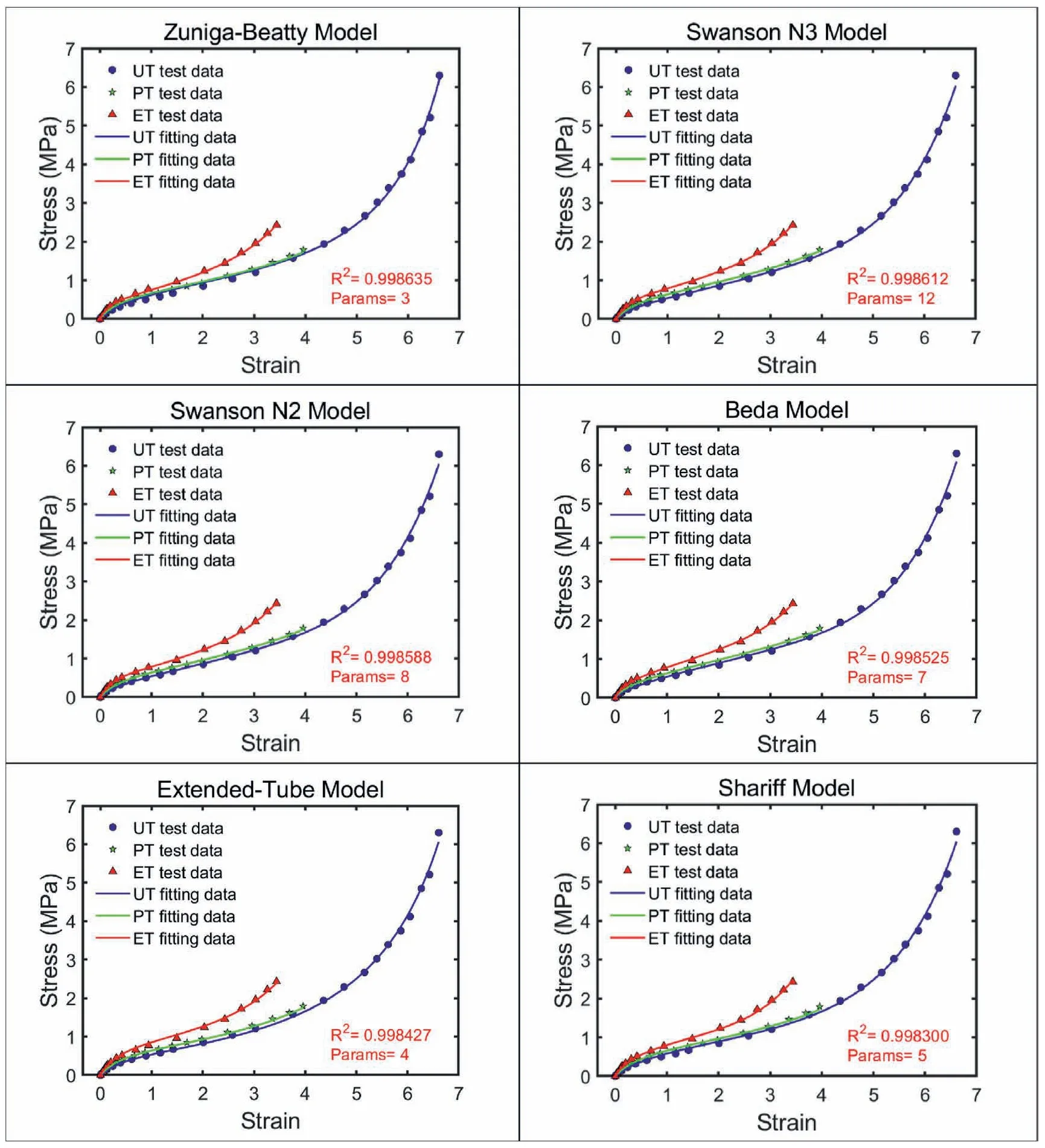
Fig.4.(continued).

The top 10 SEFs used to fit the Treloar's data based on theR2value are the Lambert Diani-Rey model,the Alexander model,the Gornet-Desmorat model,the micro-sphere model,the Zuniga-Beatty model,the Swanson N3 model,the Swanson N2 model,the Beda model,the extended-tube model and the Shariff model.Considering the good fitting results,we also provide the top 30 SEFs in the supplementary data(See Fig.S1).

TheR2values and the comparison between the test data and the fitting data for each deformation mode show that the top 10(even the top 30)SEFs can accurately reproduce complex mechanical responses under multiple deformation modes and a wide range of strains.But we have mentioned above that a good SEF should also contain as few material parameters as possible,and the material parameters of that SEF should have physical meanings.

Six SEFs with only three parameters are located in the top 30 ranking list.They are the Gornet-Desmorat model,the Zuniga-Beatty model,the Carroll model,the Lion model,the modified Flory-Erman model,and the Pucci-Saccomandi model.It is worth mentioning that the Zuniga-Beatty model and the modified Flory-Erman model are micromechanical network models.Other excellent micromechanical network models include such models as the micro-sphere model,the extended-tube model,the Edward-Vilgis model,and the network averaging tube model.In addition,the bootstrapped-8-chain model with only two parameters performs better than 50 more SEFs for the Treloar’ data of unfilled rubber.

If we don't focus on the micromechanical network models when pursuing simulation accuracy for the unfilled rubber or the filled rubber material with similarly shaped stress-strain curves,phenomenological models such as the Lambert Diani-Rey model,the Alexander model,the Gornet-Desmorat model,the Shariff model,the Carroll model and the Ogden N3 model are good choices.

The top 14 hyperelastic SEFs used to fit the UT and UC test data for the highly filled HNBR compound are shown in Fig.5.The top 6 SEFs based on theR2value are the modified Gregory model,the Gregory model,the Davis-De-Thomas model,the gen-Yeoh model,the Alexander model,and the modified Yeoh model.It is worth mentioning that all top 14 SEFs are phenomenological models.None is a micromechanical network model.This is because the stress-strain response of the highly filled HNBR is very different from the unfilled rubber or some conventional carbon black filled natural rubber material.The UT and UC stressstrain curves exhibit highly prominent nonlinear characteristics due to the formation of a filler network different from the entropic macromolecular network.It is worth mentioning that the modified Gregory model we propose in this work is perfect to describe the stress-strain response of the highly filled HNBR nanocomposite.

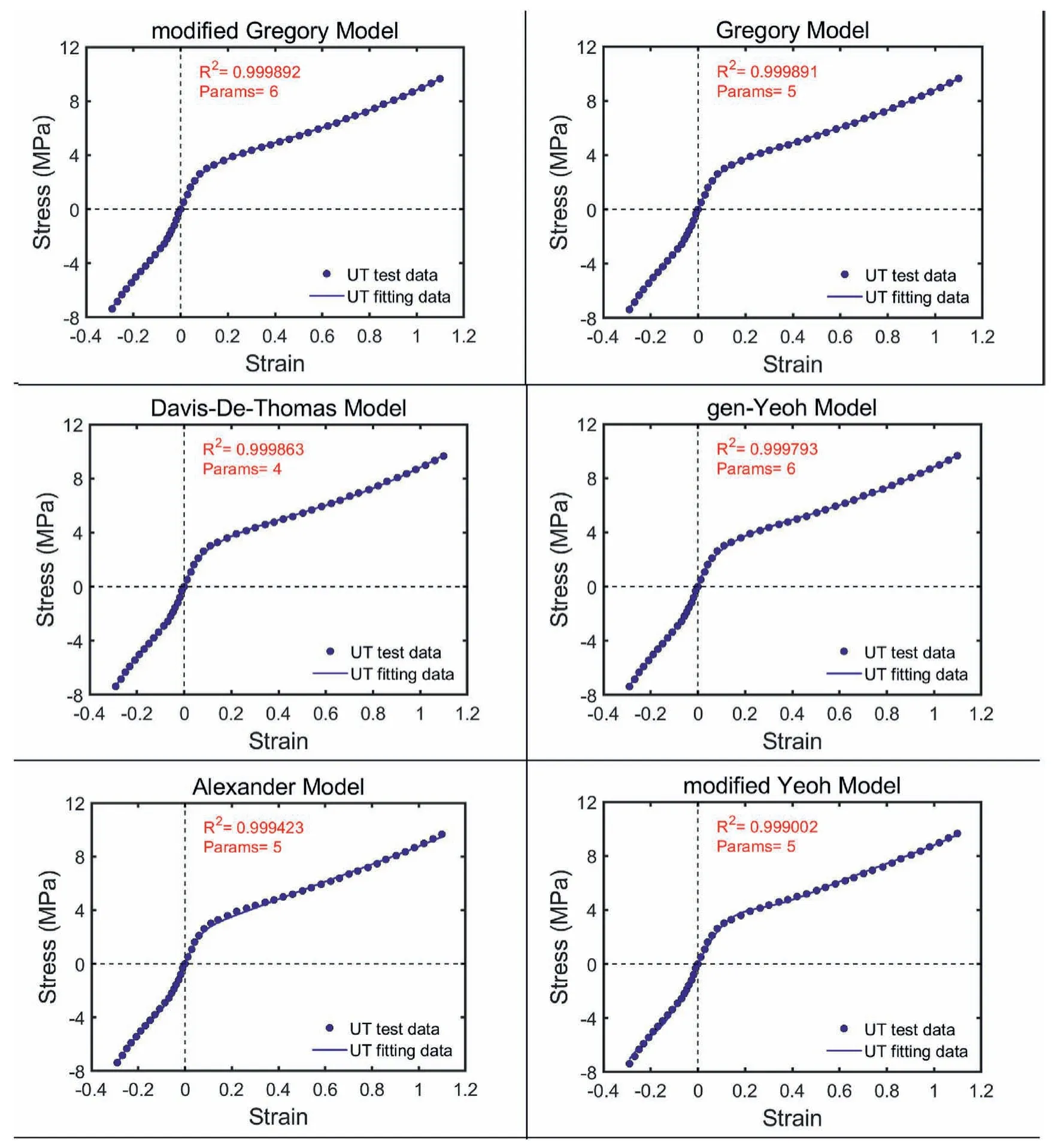
Fig.5.The top 14 SEFs used to fit the UT and UC test data for the highly filled HNBR compound.

Fig.5.(continued).

We also provide the calculated PT and ET data obtained from Eq.(18)and Eq.(21) for the top 14 SEFs.They share the same optimal material parameters fitted based on the UT and UC test data.All 14 SEFs can predict a fairly reasonable PT and ET mechanical response in a wide range of strains when only UT and UC test data are provided.The results are shown in Fig.S2.

In Figs.4 and 5,we can find that there is a very tiny difference in theR2values used to describe the nonlinear fitting accuracy for the top 10 hyperelastic constitutive models no matter whether the rubber material is unfilled or highly filled.Here we compared the number precision (or parameters sensitivity [163,164]) influence of the material parameters on theR2value.Two cases were taken into consideration:material parameters with single float and material parameters with double float.

TheR2comparison for the top 30 SEFs used to fit the Treloar's data and the top 14 SEFs used to fit the highly filled HNBR using the material parameters with single float precision and double float precision are shown in Table S4 and Table S5,respectively.Compared with theR2value calculated by the material parameters with double float precision,theR2value corresponding to the parameters with single float precision has almost no change,or the values only change slightly in the eighth or ninth decimal place.The background of these numbers has been marked in yellow,see Table S4 and Table S5.In summary,the fitting algorithm based on the nonlinear least square optimization method in this work is relatively stable.The minimal difference inR2comes from the model itself rather than numeric uncertainty.

To magnify the difference betweenR2values,we define an evaluation index(EI) that can assess which models are better than the others.

In Eq.(24),ris anR2-based quantity that can be obtained from Eq.(25).rminis the minimum value ofrfor the poorest hyperelastic model,andrmaxis the maximum value ofrfor the best hyperelastic model.The greater value ofR2leads to the bigger value ofEI,and theEIof the best hyperelastic model is 100.

TheEIvalues of the top 10 hyperelastic SEFs used to fit the Treloar's data and the test data for the highly filled HNBR compound are shown in Fig.6 and Fig.7,respectively.The SEFs in the top 10 ranking list based onEIvalues are identical to those in the top 10 ranking list based onR2values.The interesting part is the changing trend in theEIvalues.Fig.6 shows that all the 10 SEFs perform well because theEIvalue of the Shariff model,ranked 10th,is still more than 90.However,Fig.7 indicates that the first four SEFs reproduce the stress-strain response much better than the following ones.We also provide theR2,EIand Params values of the top 30 SEFs for the Treloar's data of unfilled rubber and the top 14 SEFs for the highly filled HNBR nanocomposite in the supplementary data(See Table S2 and Table S3).

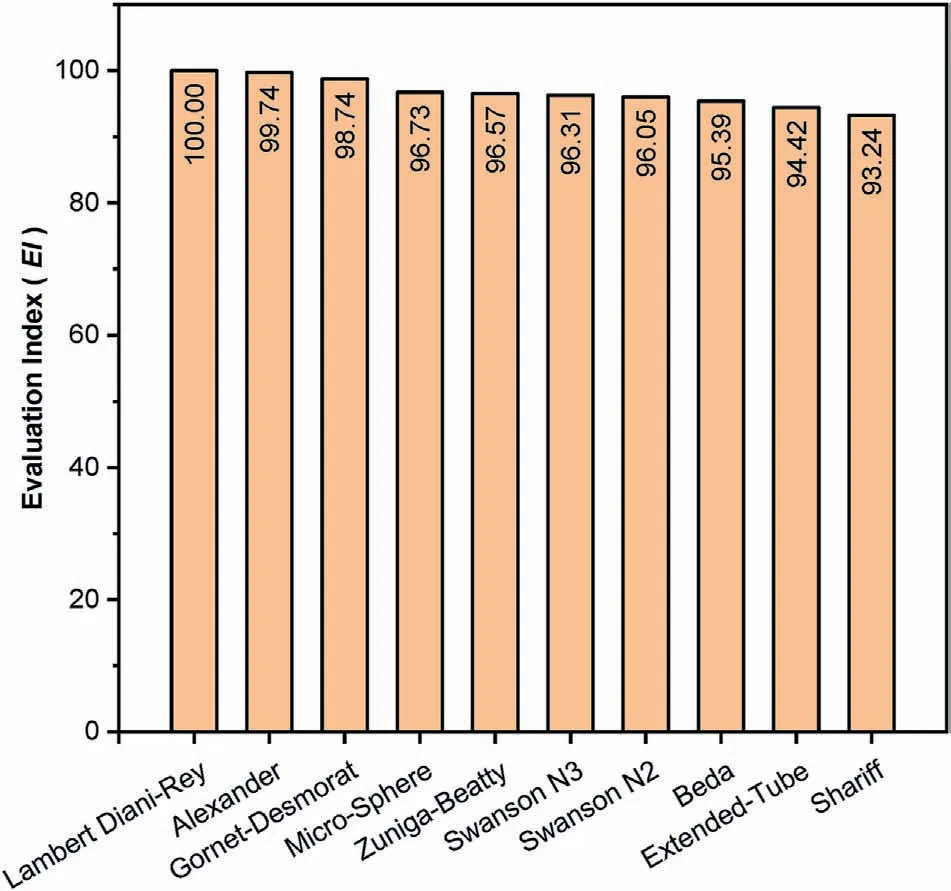
Fig.6.The evaluation index (EI) values of the top 10 SEFs used to fit the Treloar's data.

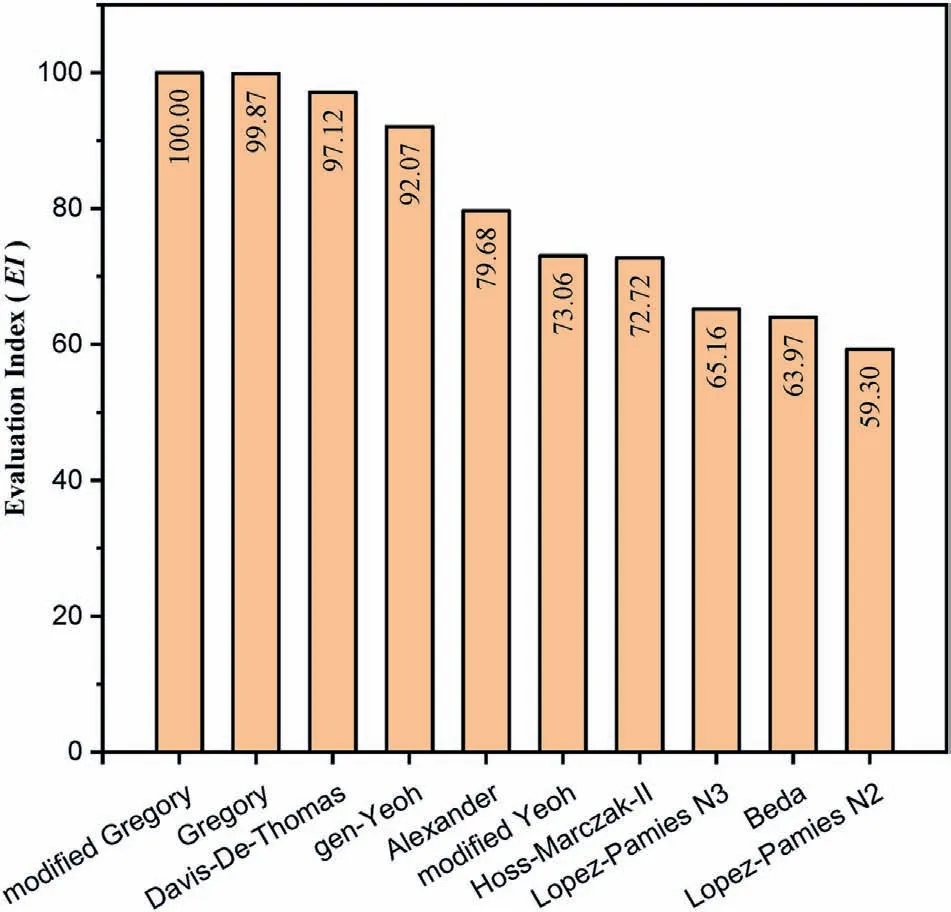
Fig.7.The evaluation index(EI)values of the top 10 SEFs used to fit the UT and UC test data for the highly filled HNBR compound.

From the fitting results of both unfilled and highly filled rubber compounds,it can be concluded that the models performing excellent fitting results for the Treloar's data usually could not display superior performance for the test data of highly filled rubber.It is worth noting that among the top 10 SEFs,only the Alexander model and the Beda model achieve satisfactory fitting results with high accuracy for both experimental data.Therefore,it is difficult to simply indicate which SEF is valid for some specific experimental data from the above comparison and discussion.The researchers and engineers need to take care when deciding the best constitutive model for the specific rubber compound at hand.But what is certain is that at least one of the 85 SEFs we reviewed is relatively suitable to describe the hyperelastic response of the RLMs.By utilizing all the SEFs to fit a specific experimental data in turn,we can help researchers and engineers carefully select the most appropriate SEF for further finite element analysis with relatively high precision.

In addition,we take the Alexander model as an example to make a general introduction of the algorithm program that can determine the final material parameters,which can be found in the last part of our supplementary file.

5.Finite element implementation of the top ranked SEFs

The determination and evaluation of the hyperelastic SEFs could not rely solely on the fitting accuracy of the model,the number of material parameters,etc.It is also important to take the computational cost into account when the SEF is used in the engineering application.

The top three SEFs (the Lambert Diani-Rey model,the Alexander model and the Gornet-Desmorat model)for the Treloar's data and the top three SEFs (the modified Gregory model,the Gregory model and the Davis-De-Thomas model)for the test data of the highly filled HNBR are all implemented with user-defined material subroutines in Abaqus/Standard(UHYPER)[73]for a three-dimensional uniaxial tensile loading problem of a dumbbell rubber specimen.

In order to distinguish the difference in computational cost of different models,we artificially refine the mesh of the finite element model.The three-dimensional model of the dumbbell rubber specimen consists of 125,307 elements(shown in Fig.8).The element type of the model was an 8-node linear hybrid,constant pressure,reduced integration brick element with enhanced hourglass control (i.e.C3D8RH in Abaqus nomenclature).The nodes at the left surface were fixed,and a displacement of 40 mm was applied to the nodes at the right surface.All the simulation work was done by using full nodal precision and 6 processors on an 8 Intel(R)Core(TM)i7-6700K CPU @4.00 GHz.

All simulation work shares the identical geometrical model,mesh model and boundary conditions.Only the SEFs differ.The computational time and Mises stress distribution of the dumbbell rubber specimen for each case are listed in Table 9 and Table 10.

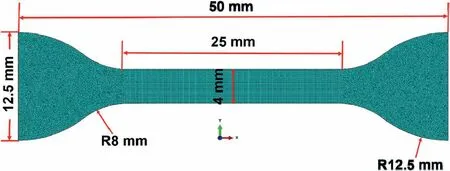
Fig.8.The three-dimensional finite element model and dimensions of the dumbbell rubber specimen composed of 125,307 elements with a thickness of 1 mm.

From Table 9,we can see that the Gornet-Desmorat model with only three material paramaters has the shortest calculation time,followed by the Alexander model,and the Lambert Diani-Rey model has the longest calculation time.The calculation results of the Mises stress distribution for the three models are very close to each other,all indicating the relatively precise prediction ability,which can be seen in Fig.9.

From Table 10,we can see that the computational time of the modified Gregory model,the Gregory model and the Davis-De-Thomas model are almost the same by using the UHYPER subroutine in Abaqus.Similarly,the Mises stress distribution calculation results of the three models are also very close to the test data,indicating that they all have very good predictive capabilities,as shown in Fig.10.The material parameters corresponding to these six models are shown in Table S6.

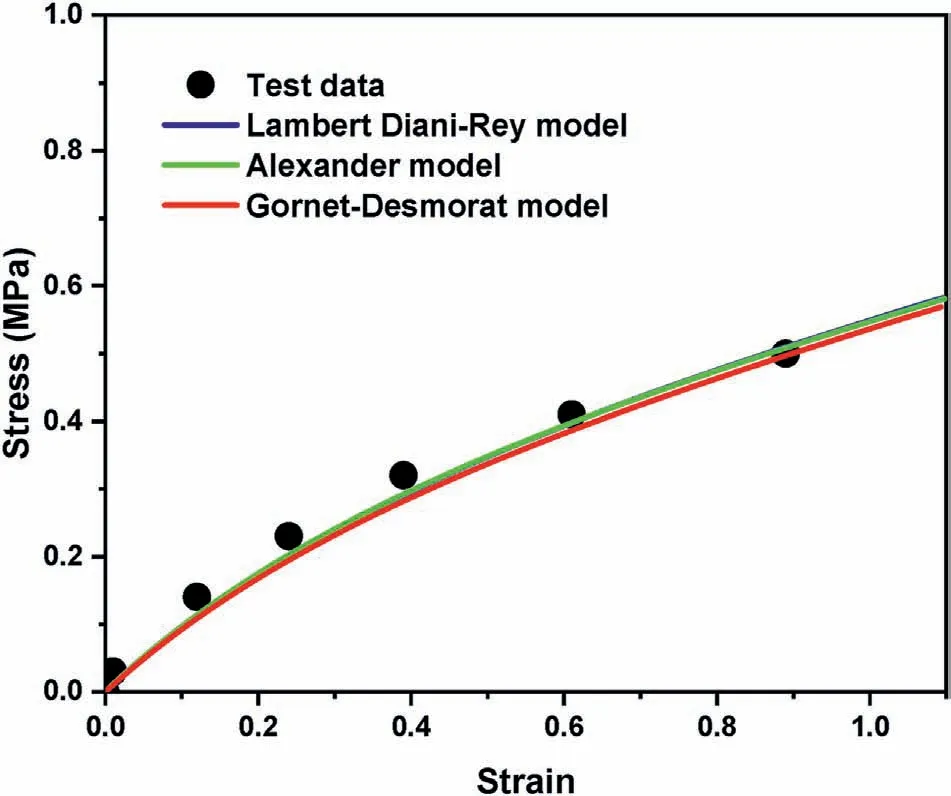
Fig.9.Comparison between test data and simulation data of the stress vs.strain curves for the Treloar's data with user-defined material subroutines in Abaqus/Standard (UHYPER).

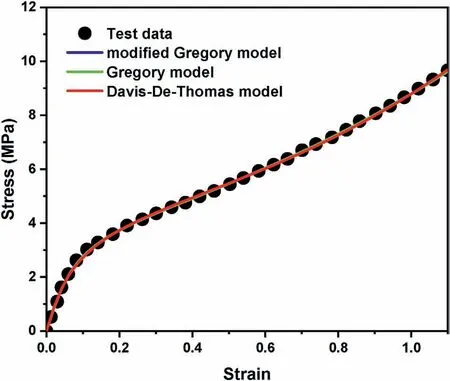
Fig.10.Comparison between test data and simulation data of the stress vs.strain curves for the highly filled HNBR with user-defined material subroutines in Abaqus/Standard (UHYPER).

6.Summary

We comprehensively reviewed 85 hyperelastic constitutive models of rubber-like materials based on the phenomenological theory and the micromechanical network theory proposed from the 1940s to the year 2019.Also,we proposed a new hyperelastic constitutive model based on the Gregory model.Then we compared all the SEFs using a nonlinear least square optimization algorithm to fit both the unfilled and highly filled rubber materials.For the unfilled rubber,the uniaxial tension,equibiaxial tension and planar tension test data of Treloar were simultaneously used.For the highly filled HNBR nanocomposite,both the uniaxial tension and the uniaxial compression test data were adopted.The ability of each SEF to reproduce the experimental data was quantitatively assessed and sorted based on a proposed evaluation index closely related to the coefficient of determination.Finally,the top three SEFs for the Treloar's data and for the test data of the highly filled HNBR were all implemented with UHYPER subroutines for a three-dimensional uniaxial tensile loading problem of a dumbbell rubber specimen to compare the computational cost.

For the unfilled rubber,the top 5 models just considering theR2value are the Lambert Diani-Rey model,the Alexander model,the Gornet-Desmorat model,the micro-sphere model,and the Zuniga-Beatty model.Six models with only three parameters are shown in the top 30 ranking list.They are the Gornet-Desmorat model,the Zuniga-Beatty model,the Carroll model,the Lion model,the modified Flory-Erman model,and the Pucci-Saccomandi model.It is particularly worth mentioning that the Zuniga-Beatty model and the modified Flory-Erman model are micromechanical network models.Other excellent micromechanical network models include the micro-sphere model,the extended-tube model,the Edward-Vilgis model,and the network averaging tube model.The bootstrapped-8-chain model with only two parameters performs better than 50 more models for the Treloar's data of the unfilled rubber.If we don't focus on the micromechanical network models when pursuing simulation accuracy for the unfilled rubber or the filled rubber material with similarly shaped stress-strain curves,phenomenological models such as the Lambert Diani-Rey model,the Alexander model,the Gornet-Desmorat model,the Shariff model,the Carroll model,and the Ogden N3 model are excellent alternatives.

For the highly filled HNBR nanocomposite,the top 5 hyperelastic constitutive models used to fit the UT and UC test data are the modified Gregory model,the Gregory model,the Davis-De-Thomas model,the gen-Yeoh model,and the Alexander model.It is worth mentioning that the top 14 models are all phenomenological models.None is a micromechanical network model.We can conclude that the models performing excellent fitting results for the Treloar's data could not display superior performance for the test data of the highly filled HNBR.Among the top 10 models,only the Alexander model and the Beda model achieve satisfactory fitting results for the experimental data of both the unfilled rubber and the highly filled rubber nanocomposite.

The computational time of the Lambert Diani-Rey model,the Alexander model and the Gornet-Desmorat model using the UHYPPER subroutine are 720s,698s,and 645s,respectively.The computational time of the modified Gregory model,the Gregory model and the Davis-De-Thomas model are almost the same.From the calculation results of the Mises stress distribution and the comparison between the test data and the simulation data of the stress vs.strain response,we can conclude that the top three ranked SEFs accurately reproduce the corresponding experimental data.

Of course,as we know,the mechanical responses of RLMs are highly nonlinear and extremely complex (not limited to hyperelasticity);for example,viscoelasticity,hysteresis,permanent set,Payne effect,Mullins effect,orthotropy or even anisotropy,aging,crack,damage,failure,etc.The stress-strain responses are also closely related to temperature,strain,frequency,strain rate,pre-stress and deformation mode.On the other hand,not so many constitutive models(compared with the number of the existing phenomenological models) are very concerned with how to quantitatively establish the relations between the complex mechanical responses and the microstructures of the rubber materials.The microstructures include the crosslinking,entanglement,orientation and crystallization of the macromolecular chains,the concentration,size,morphology,dispersion and network formation of the fillers,the interface interactions and so on.Fortunately,nowadays more and more micromechanical network models are emerging and gradually developing[165].

Putting in perspective the progress of constitutive models of RLMs in the future,we notice that a good constitutive model should quantitatively bridge the gap between the above-mentioned microstructure and the mechanical property,and accurately predict the complex mechanical responses under different working conditions and temperatures.Constitutive models of RLMs will surely and constantly develop,and they will help to predict and optimize the performance of rubber products.In addition,some novel and disruptive ideas inspired by the constitutive models,especially from the micromechanical network models,can help find better rubber-like materials.

Declaration of competing interest

None.

Acknowledgements

We gratefully acknowledge the National Key Research and Development Program of China (2018YFB1502501),and the National Natural Science Foundation of China(52003024).The authors declare that they have no conflict of interest.

Appendix A.Supplementary data

Supplementary data to this article can be found online at https://doi.org/10.1016/j.nanoms.2021.07.003.