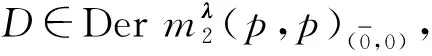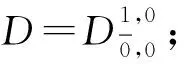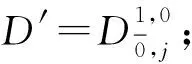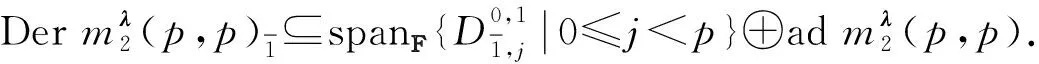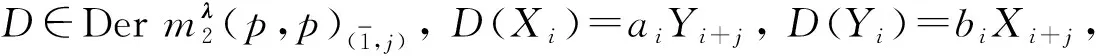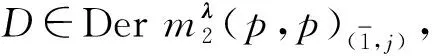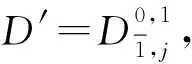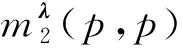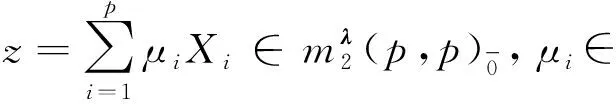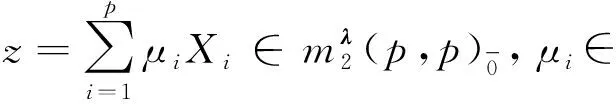張 超, 遠(yuǎn)繼霞

(黑龍江大學(xué) 數(shù)學(xué)科學(xué)學(xué)院, 哈爾濱 150080)

李超代數(shù)在理論物理和數(shù)學(xué)研究中具有重要作用. 由于基域的特征不同, 李超代數(shù)可分為模李超代數(shù)和非模李超代數(shù). 在模李超代數(shù)方面, 由于直接研究模李超代數(shù)相關(guān)理論難度較大, 因此需要在所研究的李超代數(shù)上構(gòu)造一個(gè)限制結(jié)構(gòu), 利用限制李超代數(shù)[1]相關(guān)理論進(jìn)行研究. 目前, 關(guān)于限制李超代數(shù)的研究已有很多結(jié)果, 例如: 文獻(xiàn)[2]豐富了限制李超代數(shù)的相關(guān)理論; 文獻(xiàn)[3]進(jìn)一步研究了限制李超代數(shù)的上同調(diào)理論. 線狀李超代數(shù)[4]是一類(lèi)冪零李超代數(shù), 在研究?jī)缌憷畛鷶?shù)的不可約簇中有重要作用. 文獻(xiàn)[5]刻畫(huà)了特征零的代數(shù)閉域上模型線狀李超代數(shù)的第一上同調(diào)群; 文獻(xiàn)[6]研究了一類(lèi)線狀李超代數(shù)上的Yang-Baxter方程. 超導(dǎo)子是李超代數(shù)結(jié)構(gòu)理論中的重要研究對(duì)象. 文獻(xiàn)[7]刻畫(huà)了特征零的代數(shù)閉域上Filiform李超代數(shù)Ln,m的導(dǎo)子代數(shù); 文獻(xiàn)[8]給出了系數(shù)取自伴隨模的限制李超代數(shù)1-階限制上同調(diào)是限制外超導(dǎo)子的代數(shù)解釋. 雖然關(guān)于線狀李超代數(shù)的研究已有很多結(jié)果, 但對(duì)限制線狀李超代數(shù)限制超導(dǎo)子的研究目前尚未見(jiàn)文獻(xiàn)報(bào)道.

本文首先對(duì)線狀李超代數(shù)給出其限制結(jié)構(gòu), 得到一個(gè)限制線狀李超代數(shù); 然后通過(guò)限制線狀李超代數(shù)的2×-階化結(jié)構(gòu), 得到限制線狀李超代數(shù)超導(dǎo)子的形式; 最后證明該限制線狀李超代數(shù)的超導(dǎo)子均為限制超導(dǎo)子.

1 預(yù)備知識(shí)

D([x,y])=[D(x),y]+(-1)|x|θ[x,D(y)], ?x∈hg(L), ?y∈L,

(1)

則稱(chēng)D為L(zhǎng)的2-次數(shù)為θ的齊次超導(dǎo)子.

令Derθ(L)為L(zhǎng)的2-次數(shù)為θ的齊次超導(dǎo)子構(gòu)成的集合, 其中θ∈2.定義

可證Der(L)是pl(L)的子代數(shù).稱(chēng)李超代數(shù)Der(L)是L的超導(dǎo)子代數(shù), 并稱(chēng)Der(L)的元素為L(zhǎng)的超導(dǎo)子.

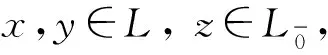
D(z[p])=(adz)p-1D(z),

則稱(chēng)D為L(zhǎng)的限制超導(dǎo)子.

令Derres.(L)α為L(zhǎng)的所有2-次數(shù)為α的限制超導(dǎo)子構(gòu)成的集合, 其中α∈2, 定義

對(duì)于任意的x∈L, adx∈Derres.(L), adL?Derres.(L)?Der(L).

下面介紹一類(lèi)線狀李超代數(shù), 給定正整數(shù)a,b∈, 設(shè)m2(a,b)是域 F上的超空間, 令

m2(a,b)=spanF{X1,…,Xa|Y1,…,Yb},

規(guī)定非零的[,]關(guān)系如下:

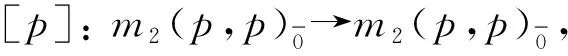
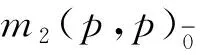
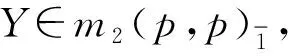
degXi=degYi=i, 1≤i≤p,

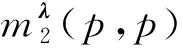
令t,s∈,是上的線性變換, 在基底上的作用如下:

(2)

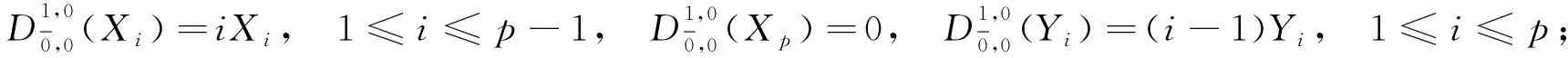
(3)

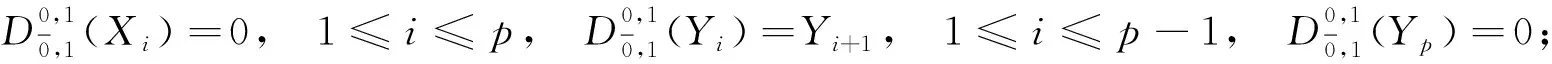
(4)

(5)

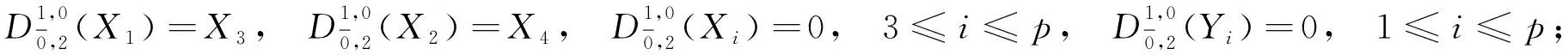
(6)

(7)

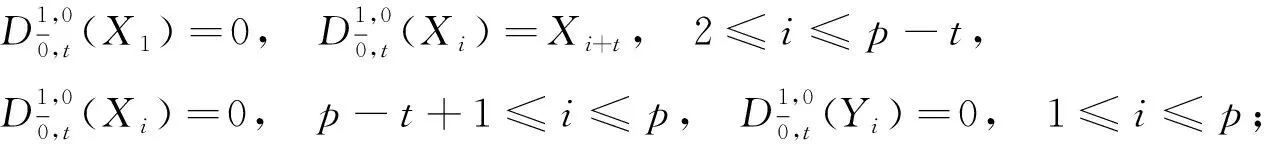
(8)

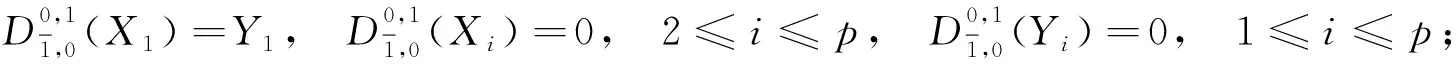
(9)

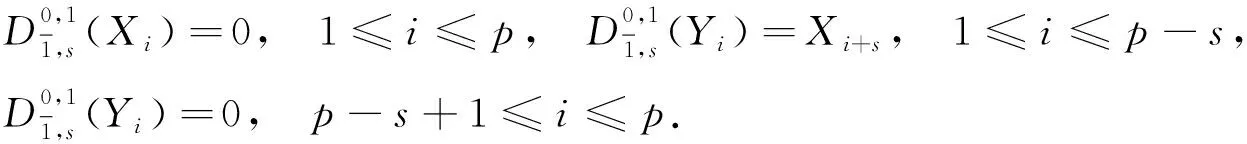
(10)

定理1令λ=(λ1,…,λp)∈Fp, 則

(11)

證明: 直接計(jì)算可得⊕關(guān)系成立.由式(1)直接驗(yàn)證易得?關(guān)系成立, 下面證?關(guān)系也成立.

① 當(dāng)j<0時(shí), 考慮以下情形.

(i) 當(dāng)j≤-p時(shí), 因?yàn)镈(X1)=…=D(Xp)=0,D(Y1)=…=D(Yp)=0, 所以D=0.

(ii) 當(dāng)-p

ai+2=ai+a2, 3≤i≤p-2.

(12)

在式(1)中令x=X1,y=Yi, 1≤i≤p-1, 可得

bi=b1+(i-1)a1, 1≤i≤p.

(13)

ai+2=ai, 3≤i≤p-j-2.

(14)

在式(1)中令x=X1,y=Yi, 1≤i≤p-1, 可得

bi=bi+1, 1≤i≤p-j-1,D(Yp-j+1)=…=D(Yp)=0.

(15)

ai+1=ai+a1, 3≤i≤p-3.

(16)

ai=ai+1=a2-a1, 3≤i≤p-j-1.

(17)

在式(1)中令x=X2,y=Xi, 3≤i≤p-j-2, 可得式(14).在式(1)中令x=X1,y=Yi, 1≤i≤p-j-1, 可得式(15).當(dāng)式(17)中的i=5時(shí), 可得a5=a2-a1.當(dāng)式(14)中的i=3時(shí), 可得a5=a3.由a5=a3=a2-a1知, 該代數(shù)的偶部基底被D作用后的系數(shù)為式(17).

當(dāng)p≤j時(shí), 因?yàn)镈(X1)=…=D(Xp)=0,D(Y1)=…=D(Yp)=0, 所以D=0.

綜上可知, 1)成立.

① 當(dāng)j<0時(shí), 考慮以下情形.

(i) 當(dāng)j≤-p時(shí), 因?yàn)镈(X1)=…=D(Xp)=0,D(Y1)=…=D(Yp)=0, 所以D=0.

(ii) 當(dāng)-p

D(X1)=a1Y1+j,ai=ai+1, 2≤i≤p-j-1.

(18)

在式(1)中取x=X2,y=Xi, 3≤i≤p-j-2, 有

ai=0, 5≤i≤p-j-2.

(19)

在式(1)中令x=X1,y=Yi, 1≤i≤p-j-1, 可得bi=bi+1, 1≤i≤p-j-1,D(Yp-j+1)=…=D(Yp)=0.當(dāng)式(18)中的i=4時(shí), 可得a5=a4, 當(dāng)式(19)中的i=5時(shí), 可得a5=0, 于是a4=a5=0, 故該代數(shù)除X1外的偶部基底被D作用為0.

(iii) 當(dāng)p≤j時(shí), 因?yàn)镈(X1)=…=D(Xp)=0,D(Y1)=…=D(Yp)=0, 所以D=0.

綜上可知2)成立.

證明: 由式(11)知, 只需證

綜上可知, 結(jié)論成立.