Inertial focusing and rotating characteristics of elliptical and rectangular particle pairs in channel flow
Pei-Feng Lin(林培鋒) Xiao Hu(胡簫) and Jian-Zhong Lin(林建忠)
1Key Laboratory of Fluid Transmission Technology of Zhejiang Province,Zhejiang Sci-Tech University,Hangzhou 310018,China
2Department of Mechanics,State Key Laboratory of Fluid Power and Mechatronic Systems,Zhejiang University,Hangzhou 310027,China
Keywords: lattice Boltzmann method,particle trains self-organization,inertial migration,particle shape
1. Introduction
The migration of particles in inertial microfluidics has gained much attention for manipulating and detecting the particles or cells in microfluidics.[1–4]The self-organization of the particle train with uniformly interparticle spacing was discovered in microchannel,which has be used for counting and screening of particles,or evenly dispersing particles into emulsions to facilitate accurate metering of drugs.[5–7]In practical biology and industry, many particles possess a variety of shapes,such as biconcave disk-like red blood cells,and cylindrical Escherichia coli,[8]the more in-depth study of the particle trains self-organization with different shapes is important in understanding the mechanism of particle train formation and improving the design of medical diagnostics and cytometry.
The mechanism of the spherical particles or the twodimensional (2D) circular particles to form the trains in microchannel flow is gradually clear. Mataset al.[7]first discovered the long-lived particle trains that had formed at the equilibrium positions, in which the force balance of the lift force and the wall repulsion acting on the neutrally buoyant particle was realized. Huret al.[9]experimentally discovered that the rigid particles in microchannel would form some single-line particle trains and staggered particle trains along the flow direction simultaneously. Hood and Roper[10]referred to those formed particle trains as the one-dimensional (1D) crystal or 2D microfluidic crystal at the equilibrium position, and developed an asymptotic theory to describe the formation of a spherical particle pair at low Reynolds number. Gaoet al.[11]studied the formation of single-line particle trains, and found that the particle train was formed after particles migrated to the equilibrium position, and the interparticle spacing of singleline particle trains was affected by the Reynolds number(Re).Kahkeshaniet al.[12]proposed that the average spacings of the single-line particle trains were 5Dand 2.6D(Dwas the particle diameter),the larger the Reynolds number,the smaller the mean spacing in single-line particle train was. Panet al.[13]found that the spacing of single-line particle trains increased withReincreasing, which was unstable whenRe> 105 orRe<21. Recently,Guptaet al.[14]and Huet al.[15]concluded that the leading particle would leave the train,the interparticle spacing increased continuously when particles migrated further downstream. For the self-organization of staggered particle trains,Schaaf and Stark[16]found that the staggered particle pairs would form three types of particle trajectories, depending on the initial position. Panet al.[13]experimentally found that the formed staggered particle trains would be affected by the initial particle position and Reynolds number.Huet al.[17]concluded that there were four types of stability conditions for forming the 2D staggered particle train in a channel flow,i.e., stable, sub-stable, dynamic, and unstable conditions.
The above studies are mainly focused on the migration of spherical particles or 2D circular particles. Owing to the rotational motion of non-circular particles, the inertial focusing and rotating characteristics are complicated.[18,19]The selforganization mechanism of non-circular particle trains is still insufficient.Chen and Nie[20]reported the power-law relationship between the rotation period of 2D elliptical particle and aspect ratio in a shear flow. The rotation period of an elliptical particle in shear flow increased rapidly with Reynolds number increasing.[21]For the migration of elliptical particles in channel flow, Masaeliet al.[22]experimentally found that the ellipsoid particle rotated around a conserved axis following the Jeffery orbits,the rotation was random at low Reynolds number. Chenet al.[23]showed that the migration process of the 2D elliptical particle in plane Poiseuille flow was dependent on the particle aspect ratio andRe. Huet al.[24]found that the 2D elliptical particles could form the single-line and staggered particle trains near walls. Huang and Lu[25]found that the rotational mode of inertial migration of ellipsoidal particles in a circular tube is significantly affected by the pipe scale and Reynolds number. Several studies about the motion of rectangular particles have been reported. Linet al.[26]discovered that the sedimentation of the short 2D rectangular particles would form the inverted“T”structures,and there existed the preferential orientations from 35?to 75?. Huret al.[27]experimental discovered that the rectangular, circular and triangle particles flowed with a periodically motion,they classified them as“focused”,“bouncing”,and“translating”,respectively. Suet al.[28]reported that the cylindrical particles had four stable equilibrium positions in a square channel, while two or four equilibrium positions were found in a rectangular channel,depending on the Reynolds number.
Based on the literature reviewed above, the researches about the effects of particle shape on the particle trains selforganization are still lacking.Therefore,the lattice Boltzmann method is used to investigate the inertial focusing and rotating characteristics of the elliptical particle pairs and rectangular particle pairs in channel flow. The interparticle spacing,equilibrium position, orientation angle in a stable rotation period are studied for the particles with different values of aspect ratio(α), and Reynolds numbers (Re), respectively. Those results will be helpful in understanding the self-organization of particle trains with various shapes in channel flow.
2. Numerical methods
2.1. Lattice Boltzmann scheme
The lattice Boltzmann method (LBM) is an efficient direct numerical simulation method to deal with the complicated geometry of the moving particles.[29–33]The single-relaxationtime LBGK model (D2Q9) with external force is adopted to obtain the channel flow:
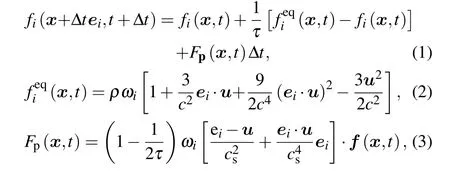

The modified bounce-back rule[35]is adopted here to ensure the no-slip boundary condition on the surface of moving particles. The hydrodynamic force and torque exerted on the particle by fluid are calculated by the momentum exchange scheme, and the force and torque exerted on the particles,when the particles cover and uncover the fluid node, are calculated by the method proposed by Aidunet al.[21]Then,the Newton’s second law is used to calculate the particle motion.The present method was described in detail and successfully verified in our previous publication.[24]
2.2. Problem definition
Now,the neutral buoyant staggered elliptical particle pair migrating in a 2D parallel plate channel is taken for example. Typical particle shapes in the present study are shown in the dashed line sided boxes in Fig. 1. The elliptical particle pair and the rectangular particle pair are abreast initially along one side or both sides of the centerline. The aspect ratioα=a/bis defined to describe the particle shape; 2aand 2bdenote the long axis and short axis of elliptical particle,or the length and width of rectangular particle, respectively.The periodic boundary and no-slip boundary condition are imposed in thexdirection and on the channel walls. The channel height isH=140?x(?x=1),it is insensitive to the trajectories of particle migration when channel length is changed from 2000?xto 2500?x. Thus,the smaller value ofL=2000?xis used. The blockage ratiokis calculated fromk=2a/Hfor the elliptical particle andk=2(a2+b2)0.5/Hfor the rectangular particle, respectively. The same blockage ratio is taken as 0.33. Reynolds numberRe=ρUmaxH/μ,whereρ,μ,andUmaxare the fluid density,viscosity,and the maximum velocity,respectively. The particles are numbered asP1andP2,and the orientation angles are represented asθ1andθ2along the flow direction. The equilibrium position is defined as the dimensionless distance from the wall(yeq/H).
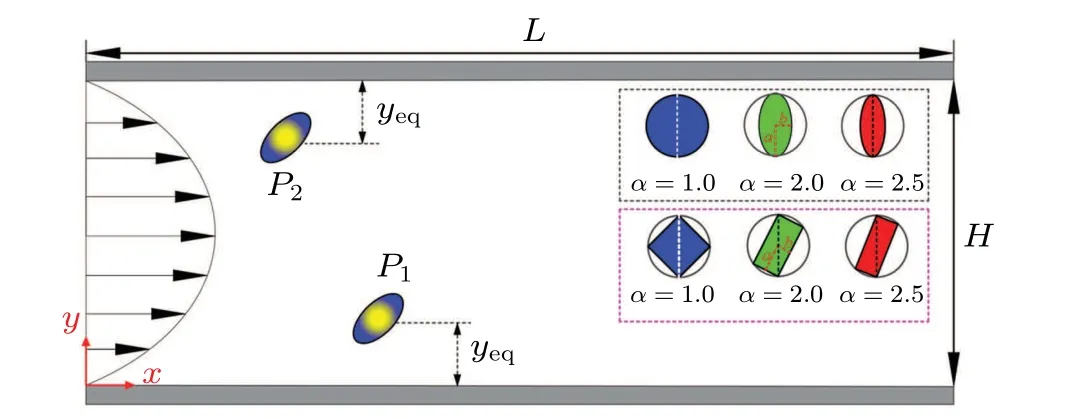
Fig.1. Schematic diagram of non-circular particle pair migration in channel flow.
2.3. Validation
The motion of a neutrally buoyant rectangular particle in Couette flow is calculated,and the evolution of orientation angleθis compared with the theoretical solution from the Jeffery’s model[36]as shown in Fig. 2. The result of orientation angle given by Jeffery is also valid for almost any fore-aft symmetry particle. The equation of orientation angleθis solved theoretically and the evolution ofθwith time is

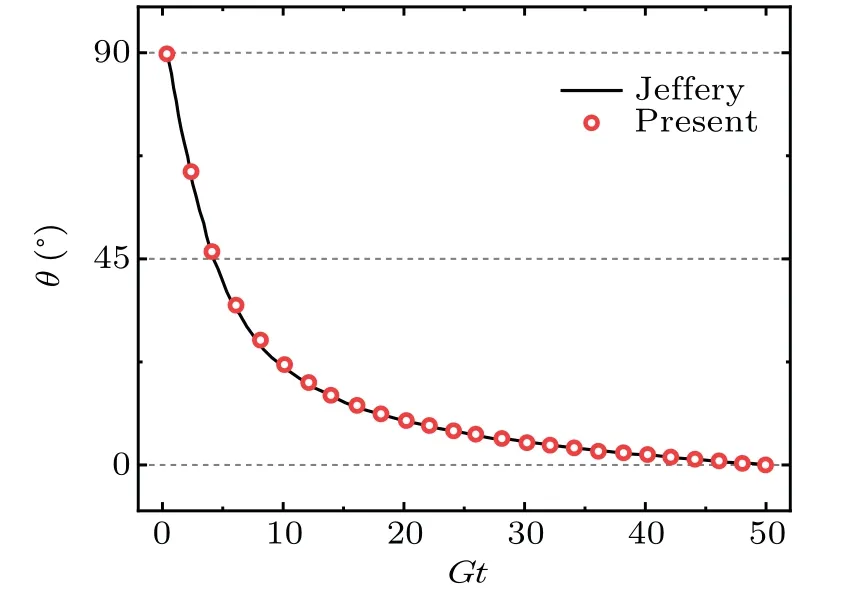
Fig.2. Orientation of rectangular particle.
3. Results and discussion
3.1. Migration of single particle
Effect of aspect ratioαon the trajectory for elliptical particle and for rectangular particle in channel flow are shown in Figs. 3(a) and 3(b). The particles with different initial positions (yin/H=0.25 and 0.4) but the same aspect ratio will finally oscillate at an identical equilibrium position,i.e., the Segr′e–Silberberg effect is valid for the migration of elliptical particle and rectangular particle in a 2D parallel plate channel.The circular particle has a smooth trajectory,the non-circular particle has an oscillatory trajectory due to the periodic rotation,and the amplitude of oscillatory trajectory decreases with aspect ratio decreasing. The phenomenon that the equilibrium position is closer to the wall at larger aspect ratio is more obvious for the elliptical particle than for the rectangular particle.

Fig. 3. Trajectories of single particle migration with different initial positions (yin/H =0.25 and 0.4, Re=32): (a) elliptical particle with different aspect ratios;(b)rectangular particle with different aspect ratios.
3.2. Self-organizing of particle pair
It has been observed that circular or spherical particles tend to form the particle train with particles evenly spaced in between in the flow direction after migrating to the equilibrium position. For the inertial migration of non-circular particles in channel flow, the evolutions of particle spacing between two particles with different initial distributions are shown in Fig. 4. Comparing with the smooth curve of the circular particles,the evolution of spacing between two neighboring non-circular particles shows a periodic curve,and fluctuates within a certain range. The upper part of Fig.4 shows that the spacing of the formed single-line particle pair is unstable (Re=32,yin=0.25, andds0=2.5), and the spacing increases with travel distance(x/H)increasing. When the aspect ratio increases,the spacing of elliptical particles changes slowly, and the change in spacing with the aspect ratio is not obvious for the rectangular particles.
Two lines of particles are distributed initially and abreast along both sides of the centerline at vertical heights ofyin=0.25Hand 0.75H,respectively. The spacing between the staggered elliptical or rectangular particles in the lower part of Fig. 4 tends to stabilize after the particles have migrated to the equilibrium positions. The same stable interparticle spacing can be achieved,no matter the initial spacingdinis 2.5 or 5.0. The travel distance to form a staggered particle pair with stable spacing increases with aspect ratio increasing.

Fig.4. Evolution of particle spacing(Re=32)in(a)elliptical particle pair and(b)rectangular particle pair,with upper panels showing initial single-line distribution particle pairs,and lower panels describing initial staggered distribution particle pairs.
Fig.5. Evolution of orientation angle of particle in(a)staggered elliptical particle pair,(b)staggered rectangular particle pair,(c)single-line elliptical particle pair,and(d)single-line rectangular particle pair,in a stable rotation period.

Fig. 6. Typical image of formed staggered particle train for (a) elliptical particles with α =2.0, (b) rectangular particles with α =2.0, (c) circular particles with α =1.0,and(d)square particles with α =1.0.
For the pair of particles that are initially abreast on both sides of the channel centerline, non-circular particles will rotate around the equilibrium position along the flow direction after reaching the equilibrium position.As shown in Figs.6(a)and 6(b),the elliptical and rectangular particle pairs form the perpendicular orientation angle,i.e.,|cos(θ1)|=|sin((0.5n+1)π±θ1)|≈|sin(θ2)|, wheren=0, 1, 2, ...,n. Thus, the cosine value ofθ1(the leading particle) and the sine value ofθ2(the lagging particle) will be mainly compared in the following to analyze the rotational characteristics in a stable rotation period. For the circular particles and square particles withα=1,figures 5(a)and 5(b)show that the relationship between the orientation angles follows the regular elliptic curve.The formation of the perpendicular orientation angle between two particles is not presented in Fig.6(c)nor in Fig.6(d). For the elliptical particle pair withα=2.0, the curve of the orientation angles is closer to the diagonal line(the dotted line in Fig.5)than for the circular particle pair,which means that the formation of the perpendicular orientation angle between the leading and lagging particles can be observed. For the rectangular particles withα=2.0, the curve of the orientation angle is partially bent. The larger the aspect ratio, the longer the time of the horizontal orientation angle(cos(θ1)≈±1)is,that is,rectangular particles prefer the horizontal orientation in a rotation period, which is consistent with the single particle migating.[37]
Figure 7 shows the typical images of the formed singleline particle train,in which the interparticle spacing is significantly greater than the formed staggered particle train.
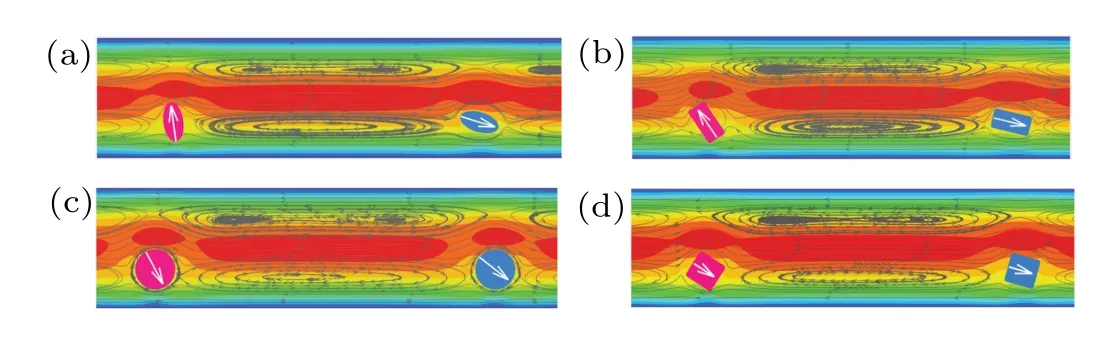
Fig. 7. Typical image of formed single-line particle train for (a) elliptical particles with α =2.0, (b) rectangular particles with α =2.0, (c) circular particles with α =1.0,and(d)square particles with α =1.0.
In Figs.5(c)and 5(d),evolutions of orientation angles of the single-line circular particle pairs and square particle pairs are similar to the regular elliptic curve of staggered particle pair (in Figs. 5(a) and 5(b)). For the elliptical and rectangular particles in Figs.7(a)and 7(b)and Figs.5(c)and 5(d),the curve of the particle orientation angle is different from the result of the staggered particle pair. The formation of the perpendicular orientation angle between two particles disappears.The curve of the orientation angle will be far from the diagonal line(the dotted line in Fig.5),which further illustrates that the single-line particle pair to form a perpendicular orientation angle is less obvious.
3.3. Effect of aspect ratio
The spacing of the single-line particle pair is unstable,only the inertial focusing and rotating characteristics of the particle pairs that are initially arranged on both sides of the centerline are analyzed at different aspect ratios (Re= 32).Regardless of the aspect ratio, the rectangular particles and elliptical particles can form the staggered particle trains with stable spacing. The equilibrium positions of the particle pair are compared with the result of the single particle migration as indicated in Fig. 8(a). The result shows that the equilibrium positions spreading range of the staggered particle pair is smaller than the single particle migrating area. The equilibrium positions are closer to the wall as the aspect ratio increases.
When the staggered particle pair with a stable spacing is formed,the the spacing varying with the aspect ratio is shown in Fig. 8(b). It can be seen that the spacing of the staggered particle pair is increased with the augment of aspect ratio,i.e.,the slender particles will have the larger interparticle spacing.The particle spacing in the elliptical particle pair is larger than in the rectangular particle pair.
The effect of aspect ratio on the orientation angle in a stable rotation period is shown in Fig. 9. With the increase of the aspect ratio of the elliptical particles, the curve of orientation angle turns closer to the diagonal line (the dotted line in Fig. 9). The curve for rectangular particles with larger aspect ratio also becomes closer to the diagonal line, the curve still remains partially bent. Figure 9 shows that the slender the particles, the easier the particle pair is to form a perpendicular orientation angle when a stable staggered particle train is formed.
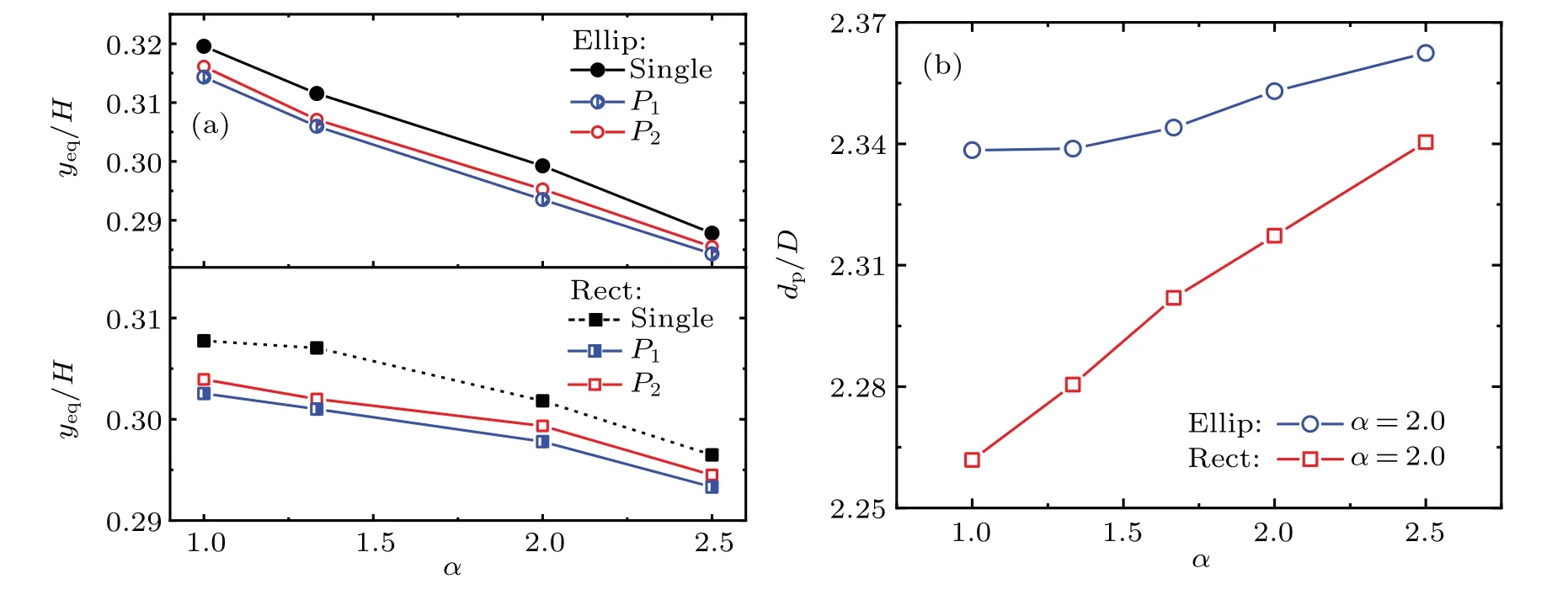
Fig.8. Effect of aspect ratio on formation of staggered particle trains for(a)equilibrium position and(b)interparticle spacing.
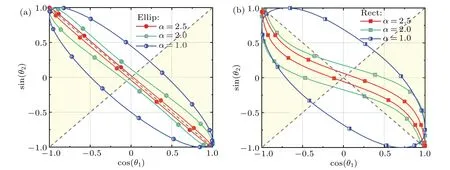
Fig. 9. Effect of aspect ratio on orientation angle of particle in (a) staggered elliptical particle pair and (b) staggered rectangular particle pair during stable rotation period.
3.4. Effect of Reynolds number
The effect of Reynolds number on the equilibrium position and the interparticle spacing of the formed staggered particle train are further compared in Fig. 10. As shown in Fig. 10(a), the equilibrium position spreading range of the staggered particle pair is smaller than the area of single particle migrating area. The equilibrium positions of circular paticles and rectangular particles are close to the wall with the increase of the Reynolds number,while the Reynolds number has little effect on the equilibrium position of elliptical particles.
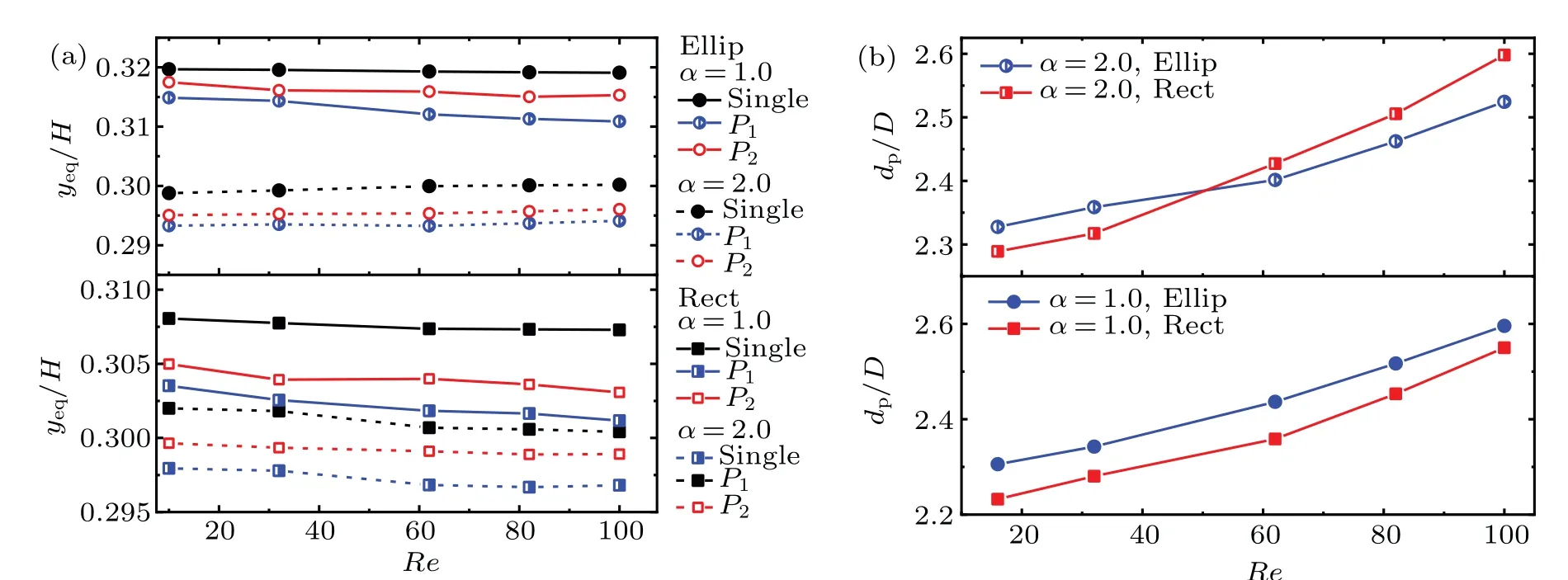
Fig.10. Effect of Reynolds number on formation of staggered particle trains,for(a)equilibrium position and(b)interparticle spacing.

Fig.11. Effect of Reynolds number on orientation angle of particle in(a)staggered elliptical particle pair and(b)staggered rectangular particle pair,during stable rotation period.
When the staggered particle pair with a stable spacing is formed, the effect of Reynolds number on the change of the interparticle spacing is shown in Fig.10(b). It can be seen that the interparticle spacing increases with Reynolds number increasing,i.e., the higher the Reynolds number, the larger the interparticle spacing is.For the circular paticles and the square particles withα=1.0,the spacing of the circular particle pair is always greater than that of the square particles. For the elliptical particles,the particle spacing is greater than that of the rectangular particles when the Reynolds number is small. The rectangular particle pair will have a larger interparticle spacing than the elliptical particle pair at a higher Reynolds number.
The influence of Reynolds number on the orientation angle of particles during a stable rotation period is shown in Fig.11. For the elliptical particle pair and the rectangular particle pair,the curves of the orientation angle are away from the diagonal line (the dotted line in Fig. 11) with the increase of Reynolds number. When the Reynolds number is 100,the orientation angle of the elliptical particles is consistent with the curve of the circular particles in Fig.5(a). For the rectangular particles, the curves are observed to be similar to each other in Fig.11(b)at different Reynolds numbers,and the rectangular particles will maintain a longer horizontal orientation angle(cos(θ1)≈±1)as Reynolds number increases. Figure 11 shows that the formation of the perpendicular orientation angle between the elliptical particle pair and rectangular particle pair is less obvious as the Reynolds number increases.
4. Conclusions
In this work, the lattice Boltzmann method is used to study the inertial focusing and rotating characteristics of elliptical and rectangular particle pairs in 2D parallel plate channel.The effects of particle shape,aspect ratio,Reynolds number on the particle rotation and train self-organization are explored.The main conclusions are obtained below.
Both elliptical and rectangular particles initially located on one side and two sides of channel centerline migrate towards the equilibrium position, forming a single-line particle train with an increasing interparticle spacing and a staggered particle train with stable interparticle spacing. The equilibrium position spreading range of the staggered particle pair is smaller than the single particle migrating area. The equilibrium position gets closer to the wall with the increase of aspect ratio and Reynolds number. The axial spacing of the staggered particle pair increases with aspect ratio and Reynolds number increasing. The staggered elliptical and rectangular particle pair can form perpendicular orientation angle, which will be more obvious at larger aspect ratio and lower Reynolds number.The single-line particles with different shapes seldom form the perpendicular orientation angles.
Acknowledgements
Project supported by the Major Program of the National Natural Science Foundation of China (Grant No. 12132015),the Natural Science Foundation of Zhejiang Province, China(Grant No. LQ22A020008), and the Key Research and Development Program of Zhejiang Province, China (Grant No.2020C03081).
- Chinese Physics B的其它文章
- Direct measurement of two-qubit phononic entangled states via optomechanical interactions
- Achieving ultracold Bose–Fermi mixture of 87Rb and 40K with dual dark magnetic-optical-trap
- New experimental measurement of natSe(n,γ)cross section between 1 eV to 1 keV at the CSNS Back-n facility
- Oscillation properties of matter–wave bright solitons in harmonic potentials
- Synchronously scrambled diffuse image encryption method based on a new cosine chaotic map
- Power-law statistics of synchronous transition in inhibitory neuronal networks

