關(guān)于非齊次樹(shù)指標(biāo)m重馬氏信源的一個(gè)強(qiáng)極限定理
金少華,田雪然
(河北工業(yè)大學(xué)理學(xué)院,天津 300401)
1.引言
樹(shù)指標(biāo)隨機(jī)過(guò)程已成為近年來(lái)發(fā)展起來(lái)的概率論的研究方向之一.強(qiáng)極限定理一直是國(guó)際概率論界研究的重要課題.楊等人在文[1]中給出了關(guān)于樹(shù)指標(biāo)非齊次馬氏鏈的廣義熵遍歷定理.ZHONG等在文[2]中通過(guò)引入樹(shù)指標(biāo)馬爾科夫鏈的概念,證明了Cayley樹(shù)指標(biāo)下馬爾科夫鏈關(guān)于二元函數(shù)延遲和的一個(gè)強(qiáng)極限定理.ZHONG等在文[3]中首先引入漸近對(duì)數(shù)似然比作為二叉樹(shù)上任意隨機(jī)場(chǎng)與分叉馬爾科夫鏈之間偏差的度量,然后通過(guò)構(gòu)造一個(gè)非負(fù)鞅,建立了二叉樹(shù)指標(biāo)馬爾科夫鏈的一類(lèi)強(qiáng)偏差定理.WANG等在文[4]中給出了連續(xù)狀態(tài)非齊次馬氏鏈滑動(dòng)平均的強(qiáng)大數(shù)定律.李世林等人在文[5]中研究了在有限狀態(tài)空間取值的二叉樹(shù)上非齊次馬氏鏈轉(zhuǎn)移概率調(diào)和平均的極限性值.金少華等人在文[6]中給出了非齊次樹(shù)上馬氏雙鏈轉(zhuǎn)移矩陣的一個(gè)強(qiáng)極限定理.本文通過(guò)引入相對(duì)熵密度偏差的概念和構(gòu)造非負(fù)鞅,研究給出了關(guān)于非齊次樹(shù)指標(biāo)m重馬氏信源的一個(gè)強(qiáng)極限定理.
2.基本概念
設(shè)T是一個(gè)具有根頂點(diǎn)o的無(wú)限樹(shù),{Nn,n ≥1}是一列正整數(shù)集,如果T的第n(n ≥0)層上的每個(gè)頂點(diǎn)均與第n+1層上的Nn+1個(gè)頂點(diǎn)相鄰,則稱(chēng)T為廣義Bethe樹(shù)或廣義Cayley樹(shù).特別地,若對(duì)非負(fù)整數(shù)集N,用模m的同余關(guān)系對(duì)其分類(lèi)得到如下模m的剩余類(lèi)
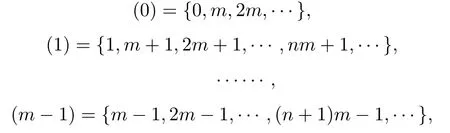

3.強(qiáng)極限定理




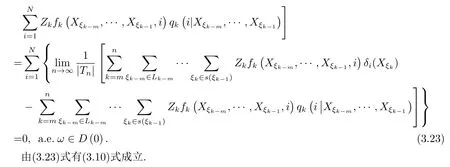
——基于二叉樹(shù)的圖像加密
- 應(yīng)用數(shù)學(xué)的其它文章
- 一類(lèi)線性離散時(shí)間系統(tǒng)的預(yù)見(jiàn)控制器設(shè)計(jì)
- Global Boundedness to a Quasilinear Attraction-repulsion with Nonlinear Diffusion
- Trudinger-Moser Inequality Involving the Anisotropic Norm with Logarithmic Weights in Dimension Two
- 相依風(fēng)險(xiǎn)結(jié)構(gòu)下彈性ò休c金產(chǎn)品價(jià)?風(fēng)險(xiǎn)比較
- Superconvergence Analysis of Anisotropic Linear Triangular Finite Element for Multi-term Time Fractional Diffusion Equations with Variable Coefficient
- Infinitely Many Sign-changing Solutions for a Quasilinear Choquard Equation

