Pressure-induced novel structure with graphene-like boron-layer in titanium monoboride
Yuan-Yuan Jin(金園園) Jin-Quan Zhang(張金權(quán)) Shan Ling(凌山) Yan-Qi Wang(王妍琪) Song Li(李松)Fang-Guang Kuang(匡芳光) Zhi-Yan Wu(武志燕) and Chuan-Zhao Zhang(張傳釗)
1Department of Physics and Optoelectronic Engineering,Yangtze University,Jingzhou 434023,China
2School of Physics and Electronic Information,Gannan Normal University,Ganzhou 341000,China
3College of Electronic and Electrical Engineering,Henan Normal University,Xinxiang 453007,China
The recent discovery of the novel boron-framework in boron-rich metal borides with complex structures and intriguing features under high pressure has stimulated the search into the unique boron-network in the metal monoborides or boron-deficient metal borides at high pressure. Herein, based on the particle swarm optimization algorithm combined with first-principles calculations, we thoroughly explored the structural evolution and properties of TiB up to 200 GPa.This material undergoes a pressure-induced phase transition of Pnma →Cmcm →Pmmm. Besides of two known phases Pnma and Cmcm, an unexpected orthorhombic Pmmm structure was predicted to be energetically favored in the pressure range of 110.88–200 GPa. Intriguingly,the B covalent network eventually evolved from a one-dimensional zigzag chain in Pnma-TiB and Cmcm-TiB to a graphene-like B-sheet in Pmmm-TiB.On the basis of the microscopic hardness model,the calculated hardness(Hv)values of Pnma at 1 atm,Cmcm at 100 GPa,and Pmmm at 140 GPa are 36.81 GPa,25.17 GPa,and 15.36 GPa,respectively. Remarkably,analyses of the density of states,electron localization function and the crystal orbital Hamilton population(COHP)exhibit that the bonding nature in the three TiB structures can be considered as a combination of the B–B and Ti–B covalent interactions. Moreover, the high hardness and excellent mechanical properties of the three TiB polymorphs can be ascribed to the strong B–B and Ti–B covalent bonds.
Keywords: transition-metal boride,high pressure,first-principles,phase transition
1. Introduction
Metal borides (MBs) have attracted significant attention in both the fundamental research and industrial applications.The diversity of boron bonding in solids facilitates the realization of various materials with fantastic properties including the super hardness, superconductivity and so on.[1]In transition-metal borides, such as ReB2, OsB2and WBx, the strong B–B covalent network promotes the mechanical performance, bringing about the super hardness.[2–4]Magnesium diborides (MgB2) present a considerable superconducting transition temperature of 39 K, driven by a stiff sp2B–B network.[5–7]
Generally,high pressure can effectively reduce the interatomic distances of the materials and thus significantly alter the electronic structures and bonding forms, leading to the formation of new materials with strange physical and chemical properties.[6,8,9]In metal borides,the pattern of the boron network that is covalently able to form various dimensional networks exhibits unexpected transformations under pressure.A high-pressure investigation on MgB2indicated that the ambient AlB2-type phase transforms into a high-pressure orthorhombic KHg2polymorph, resulting from the strong outof-plane distortions of the two-dimensional honeycomb boron sublattice to a peculiar tetrahedrally bonded three-dimensional boron network.[10]Afterward, a number of remarkable studies on the pressure-induced evolution of FeB4, RuB4and OsB4,[11–14]verified that FeB4and OsB4undergo a metalto-semiconductor phase transition while all the stable structures of RuB4are metal or semimetal. The mechanism behind these phenomena could be mainly ascribed to the evolution of the boron framework. Besides, pressure caused the phase transitions of BeB6, MgB6, CaB6, SrB6, BaB6, YB6and ScB6,[15–21]together with the variation of physical properties. The boron covalent network in these metal hexaborides undergoes a fantastic transformation process. For instance,SrB6, a member of the rare-earth hexaborides family, crystallizes in a cubic structure (space groupPm-3m) at ambient pressure,which transforms into an orthorhombic structure(Cmmm)upon increasing pressure,with further transformation to a tetragonal structure (I4/mmm) at 60 GPa.[18]The boron framework eventually evolves from B6octahedron in the cubicPm-3mphase to twinned pentagonal bipyramids in theCmmmstructure to twinned augmented triangular prisms inI4/mmmphase. Moreover, theoretical calculations showed that ScB6undergoes a phase sequence ofP21/m →C2/m →Cmcmunder high pressure.[21]At the same time, the evolution of the boron framework is from a graphene like layer to a planar B4 ring, B6 and B7 cycle, and non-planar B8 cycle, which interconnect a graphene-like network. Although considerable efforts have been paid to probing into the pressure-induced phase transition and boron framework evolution in the metal borides on the boron-rich side,there is scant information about the metal borides with relatively low boron content. To better understand the structural and boron-network evolution under pressure, it is extremely desirable to explore these extraordinary phenomena in the metal borides with the M/B stoichiometric ratio of one and less than one as well.
Among the metal borides,the titanium borides are probably the technologically most important binary system because the borides in the Ti–B binary system are widely used in various fields: rocket engineering, aircraft engineering, thin film interconnection, as biological implants,non-oxide ultrahigh-temperature structural ceramics and solid heat-resistant coatings for various products, etc.[22–24]In the Ti–B binary system, three intermetallic compounds TiB,Ti3B4,and TiB2have already been identified by the experimental measurements.[25–27]The previously conventional wisdom indicated that the strength or hardness possesses a positive correlation with the boron content but the recent theoretical investigations exhibited an anomalous phenomenon in the mechanical response under changing boron concentration.[28]So, it is really necessary to probe into the crystal structures and mechanical properties of the titanium borides with the low boron content. Among the stable titanium borides, TiB has the lowest boron concentration and is used as an effectivein-situformed reinforcement in titanium alloy matrix composites(TAMCs),TiB has higher modulus,and higher strength at both room and elevated temperatures than the Ti alloys.[29,30]Therefore,many investigations have concentrated on the crystal structure and the mechanical properties of TiB experimentally and theoretically. Decker and Kasper[25]firstly proposed that TiB crystallizes into the FeB-type structure with the orthorhombicPnmasymmetry. By the nanoindentation technique,it was identified directly by Caoet al.that the TiB has the high elastic modulus (E=450 GPa) and high hardness(Hv= 27.5 GPa).[31]On the basis of high resolution transmission electron microscopy (HRTEM) and x-ray diffraction(XRD)techniques,Huet al.confirmed a NaCl-type face centered cubic structure with space groupFm3mof TiB, which is in contrast with the orthorhombicPnmastructure.[32]Two recent theoretical investigations on the structural stabilities of various phases of TiB demonstrated that the orthorhombicPnmaconfiguration is most stable at ambient pressure.[33,34]Despite several phases of TiB studied under atmospheric pressure, the high-pressure phases of TiB remain completely unexplored. It stimulates us to probe into the phase transition and boron-network evolution of TiB over a broad pressure range,in quest to explore its new structures and complex boron framework types.
In the current work, we aim to explore the phase behaviors and boron-network evolution of TiB within the pressure range of 0–200 GPa with the aid of the advanced global structural search methodology[35,36]in combination with the firstprinciples calculations. The present study uncovers a hitherto unknown high-pressure TiB configuration, orthorhombicPmmmwith the intriguing graphene-like B-sheet, which is firstly found in the transition metal monoboride.The structural transition order for TiB under pressure is identified asPnma →Cmcm →Pmmm. In addition, we have further probed into their structural characters, mechanical and electronic properties and bonding features. These results provide a general route to explore novel boron layer structures in the transition metal monoboride under high pressure.
2. Methods
In this work, we performed the structure prediction of TiB containing up to 8 formula units (f.u.) at selected pressures of 0 GPa,50 GPa,100 GPa,150 GPa and 200 GPa using a particle swarm optimization algorithm as implanted in the CALYPSO code.[35–37]This method can effectively find the ground-state and low-energy metastable structures with only the given chemical composition,which has been successfully demonstrated by various applications ranging from elemental solids to binary and ternary compounds.[38–48]The detailed descriptions about this structural search methodology can be found in Refs.[35,36].
The subsequent geometrical optimizations, electronic structures and mechanical properties calculations were performed within density functional theory under the Perdew–Burke–Ernzerhof (PBE) functional of the generalized gradient approximation (GGA) as implemented in the Viennaab initiosimulation package (VASP) code.[49,50]The projector augmented wave (PAW) method was adopted to describe the electron–ion interactions with 3s23p63d24s2and 2s22p1treated as the valence electrons for the Ti and B atoms, respectively.[51]An energy cutoff of 800 eV for the expansion of the wave function into plane waves and appropriate Monkhorst–Packkmeshes were selected to ensure a force convergence threshold of 1 meV/atom.[52]To investigate the dynamical stabilities of the considered structures,the phonon dispersion calculations were carried out by employing a supercell approach within the Phonopy code.[53,54]The chemical bonding and the interatomic interaction analysis were performed through the crystal orbital Hamilton population (COHP) method implemented in the LOBSTER code.[55,56]When the individual elastic constants were derived, the bulk moduli (B), Young’s moduli (E) and shear moduli (G), and Poisson’s ratio (ν) were obtained by using Voigt–Reuss–Hill approximation (VRH).[57]The theoretical Vickers hardness was estimated based on the empirical model,Hv=2.0(k2G)0.585-3.0,wherek=G/B.[58]
3. Results and discussion
3.1. Structure prediction and phase transition under pressure
As we all know, external pressure has a great influence on the crystal structure of materials, so different stable structures may be found under different pressures.[59]In order to predict potential high-pressure crystal structures and phase transition of TiB, we predicted the low-energy crystal structures from 0 to 200 GPa by an interval of 50 GPa with 1–8 unit formula cells for TiB.Based on the CALYPSO structure prediction method,five low-energy candidate phases are confirmed, namely, the orthorhombicPnma-TiB, orthorhombicCmcm-TiB, cubicFm-3m-TiB, tetragonalI41/amd-TiB, and orthorhombicPmmm-TiB phases. These five candidate crystal structures diagrams of TiB are shown in Fig.S1 of the supplementary information(SI)and the corresponding structural information is tabulated in Table S1. The previous known structures includingPnma-TiB,[25,60]Cmcm-TiB,[33,34]Fm-3m-TiB[32]andI41/amd-TiB,[33]were successfully reproduced in the specific pressure range, which suggests that the methodology used in present work is applicable to TiB. To elucidate the phase diagram of TiB, figure 1(a) provides the enthalpy differences of the five candidate crystals of theCmcm-TiB.Under atmospheric pressure, the most stable phase is an orthorhombicPnma-TiB structure and belongs to the FeBtype monoboride, which is in excellent agreement with the previous experimental and theoretical results.[25,60]When the pressure increases to 69.08 GPa, the orthorhombicCmcm-TiB phase is favored over thePnma-TiB phase in the pressure range of 69.08–110.88 GPa. Upon further compression,orthorhombicPmmm-TiB has the lowest enthalpy among the candidate phases. Thus, the sequence of the structural transformation for TiB within the pressure range of 0–200 GPa isPnma-TiB→Cmcm-TiB→Pmmm-TiB. This phase transformation is also supported by the volume–pressure relations(V–P) in Fig. 1(b), as we observed that thePnma →CmcmandCmcm →Pmmmphase transitions have discontinuous changes in volume at the transition point with volume collapses of 0.16% and 1.8%, suggesting that the three phase transitions are the first-order nature rather than continuous. Additionally,the relative stability of TiB in comparison with other Ti–B phases was confirmed by comparing the formation enthalpies(ΔHf) of known Ti–B phases at 1 atm, 70 GPa and 150 GPa,as depicted in Fig. S2. As shown in Fig. S2(a), under atmospheric pressure,the calculated ΔHfof four Ti–B compounds(TiB,Ti3B4,Ti2B3and TiB2)are exactly located at the curves of convex hull, which is consistent with the previous results derived by Liet al.,[33]confirming the TiB thermodynamic stability under ambient pressure. Furthermore, the ΔHfof theCmcm-TiB phase at 70 GPa and thePmmm-TiB phase at 150 GPa reach-1.099 eV/atom and-1.179 eV/atom,respectively,and slightly above the convex hull,demonstrating their excellent thermodynamic stability. The above results indicate thatCmcm-TiB andPmmm-TiB are excellent metastable phases, which can be synthesized under particular temperatures. Moreover, the stability of TiB can be further verified by the preceding experiment.[25,31]In this work, we focus on the detailed structural feature and the related properties of thePnma-TiB phase at 1 atm, theCmcm-TiB phase at 100 GPa,and thePmmm-TiB phase at 140 GPa.
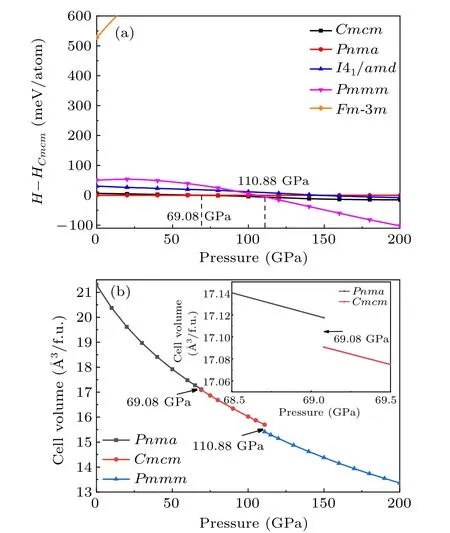
Fig.1. (a)Enthalpy–pressure relation with respect to the Cmcm phase and(b)volume–pressure relations for TiB.
3.2. Structure feature and dynamical stability
To completely elucidate the structural character of thePnma-TiB phase at 1 atm, theCmcm-TiB phase at 100 GPa,and thePmmm-TiB phase at 140 GPa,we depicted their crystal structures in Fig. 2 and tabulated their homologous structural parameters in Table 1. In Table 1,the lattice parameters of thePnmaphase under atmospheric pressure are consistent with the preceding experimental and theoretical results. In thePnmaphase at 1 atm(see Fig.2(a)),one Ti atom is surrounded by 7 neighboring B atoms with the Ti–B separations varying from 2.353 ?A to 2.558 ?A, forming a distorted TiB7enneahedron. In this phase, the nearest Ti–B distance of 2.353 ?A is slightly less than the sum(2.29 ?A)of the covalent radii of the B atom (0.84 ?A) and the Ti atom (1.45 ?A), indicating a covalent bond between the Ti and B atoms. In addition, the B atoms form one-dimensional zigzag chain with the identical B–B length of 1.812 ?A alongb-axis and identical B–B–B angle of 114.89°. This B–B bond length is comparable to that ofα-B(1.669–2.003 ?A),[61]γ-B(1.661–1.903 ?A),[62]Pnma-ScB3andP63mc-ScB6,[63]uncovering a strong B–B covalent bond. Hence, thePnma-TiB phase is composed of the distorted TiB7enneahedron and one-dimensional zigzag chain of B atoms. For theCmcmphase at 100 GPa, the basic building block can be considered as slightly distorted TiB7octahedron with one Ti–B distance of 2.263 ?A, two Ti–B distances of 2.183 ?A and four Ti–B distances of 2.148 ?A. Along theb-axis, the apical B atom and four baseplane B atoms form a rectangular pyramid. Moreover, four baseplane B atoms and two underlying B atoms form a triangular prism. The Ti–B bond lengths varying from 2.148 ?A to 2.263 ?A are all shorter than the sum(2.29 ?A)of the covalent radii of the Ti and B atoms, declaring the relatively strong Ti–B covalent bonding. Meanwhile, the B atoms also exhibit one-dimensional zigzag chain with the uniform length of 1.678 ?A along thecaxis and an identical B–B–B angle of 112.87°. These results suggest that theCmcm-TiB configuration consists of slightly distorted TiB7octahedron and one-dimensional zigzag-like B chain. Interestingly, thePmmmphase at 140 GPa has two nonequivalent B positions,namely,B1 located at the Wyckoff site 2t(0.5000,0.5000,0.2940)and B2 occupying the Wyckoff site 2r(0.0000, 0.5000, 0.6017). The Ti atoms take three different sites(ie.,Ti3,Ti4 and Ti5),the Wyckoff 2q(0.0000,0.0000,0.7930),1d(0.5000,0.0000,0.5000)and 1f(0.5000,0.5000,0.0000)positions. The Ti3 atom is surrounded by four B1 atoms with the Ti–B distance of 2.104 ?A and two B2 atoms with the Ti–B distance of 2.122 ?A, forming a TiB6octahedron.The Ti4 atom is connected with twelve adjacent B atoms including four B1 and eight B2 atoms with the corresponding Ti–B distances of 2.151 ?A and 2.118 ?A, forming a TiB12hexagonal prism. Two B1 atoms are at either end of the B5 atom with an identical Ti–B separation of 2.189 ?A.More importantly,two B1 and four B2 atoms form a two-dimensional six-membered B ring,with the same B1–B2 bond distance of 1.594 ?A and the identical B2–B2 bond distance of 1.618 ?A.The above results demonstrate that strong Ti–B and B–B covalent bonds exist in this structure. Thus,thePmmm-TiB structure contains the TiB6octahedron,TiB12hexagonal prism and two-dimensional six-membered B ring.This planar boron network can also be seen in other borides such as LiB,MgB2and FeB4.[7,12,64]It is obvious that the Ti–B and B–B bond lengths gradually decrease with the increasing pressure, which coincides with the reduction of atomic distance caused by high pressure. It also shows that the interaction between Ti–B and B–B becomes stronger with the rise of pressure. In the structures under the increasing pressure, the basic B–B covalent network transforms from the one-dimensional zigzag chain to two-dimensional B ring. Increasing the pressure in the compound tends to promote the formation of the higher dimension B–B network.
In order to assess the dynamical stability of the three considered phases at the specific pressures (thePnma-TiB phase at 1 atm,theCmcm-TiB phase at 100 GPa and thePmmm-TiB phase), we further calculated their phonon spectra, as illustrated in Fig. 3. The absence of any imaginary phonon frequencies in the entire Brillouin zone confirms that all three concerned configurations are dynamically stable.[65,67–69]

Fig.2.Crystal structures of three considered phases.(a)Pnma-TiB at 1 atm,(b) Cmcm-TiB at 100 GPa and (c) Pmmm-TiB at 140 GPa. The green and red spheres represent boride and titanium atoms,respectively.
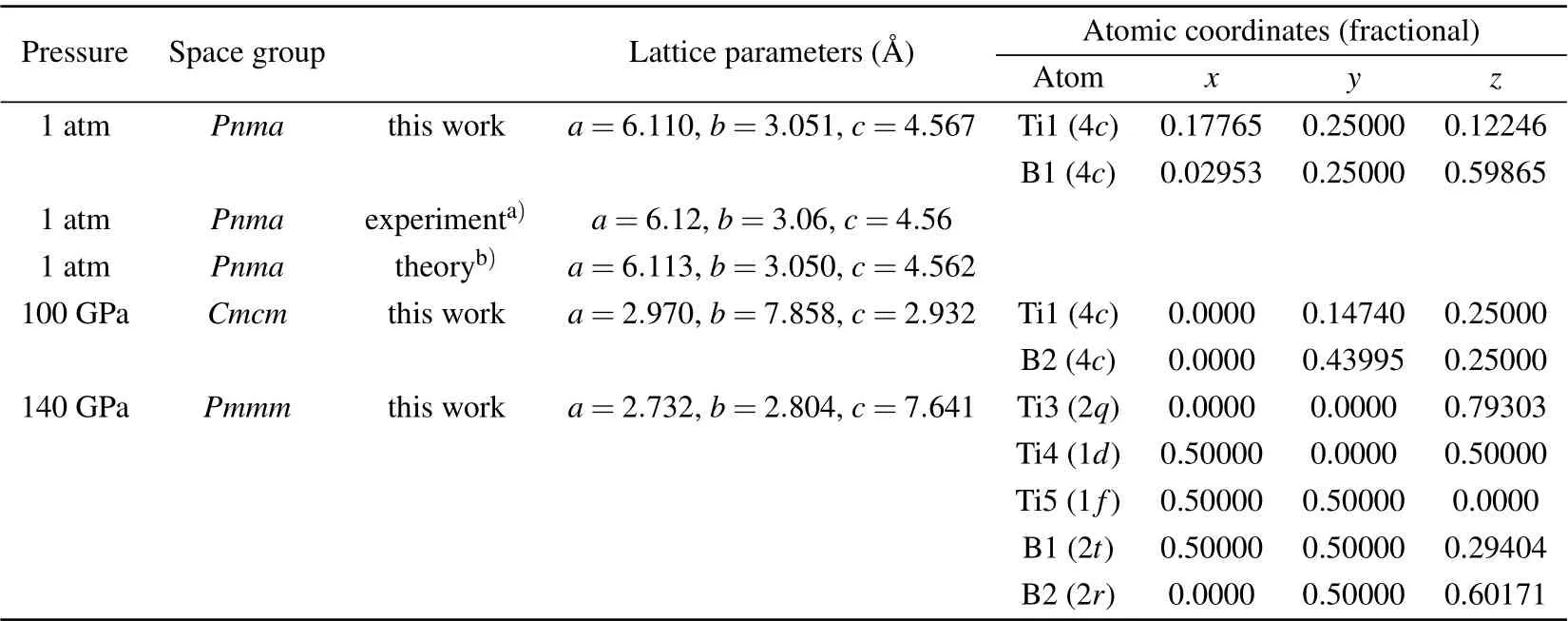
Table 1. Structural parameters of TiB for the Pnma phase at 1 atm,the Cmcm phase at 100 GPa,and the Pmmm phase at 140 GPa.
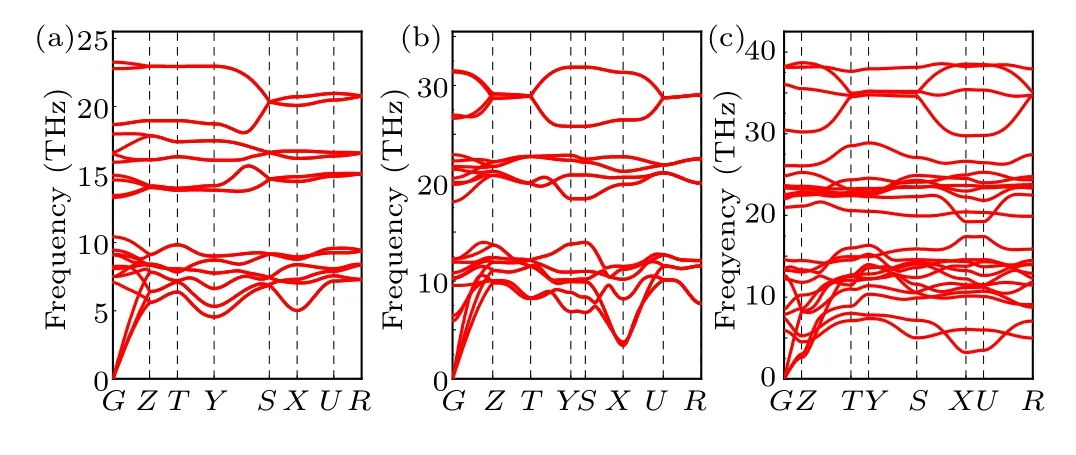
Fig. 3. Phonon dispersions for (a) Pnma-TiB at 1 atm, (b) Cmcm-TiB at 100 GPa and(c)Pmmm-TiB at 140 GPa.
3.3. Mechanical properties and hardness under high pressure
Mechanical stability plays a significant role in the stabilization of a material. To clarify the mechanical stability of the three considered structures under the selected pressures,the elastic constants were derived by using the strainstress method, as summarized in Table 2. These three concerned phases belong to the orthorhombic crystal phase and meet the corresponding mechanical stability condition of the orthorhombic phase, which verifies the mechanical stability of the three considered structures.[70]Simultaneously, to evaluate the mechanical performance of the three phases under the corresponding pressure, the bulk modulus (B), shear modulus (G),B/Gratio, Young’s modulus (E) and Poisson’s ratio(ν) were also calculated (see Table 2). It is obvious that the calculated elastic constants, bulk modulus, shear modulus,Young’s modulus and Poisson’s ratio ofPnma-TiB are in consistent with preceding theoretical results,[33,60]confirming the reliability of the present methodology. As we all know, theC11,C22andC33denote the linear incompressibility along the correspondinga-,b-andc-axes. As tabulated in Table 2, the value ofC22forPnma-TiB andCmcm-TiB is higher than that ofC11andC33, revealing that both phases possess stronger incompressibility along theb-axis than that along thea- andc-axes. At the same time, the larger value ofC11than that ofC22andC33inPmmm-TiB verifies that its incompressibility along thea-axis is stronger than that along theb- andc-axes.C44is a crucial indicator to the indentation hardness of a crystal. The calculatedC44values of the three concerned structures exceed 170 GPa, revealing their strong strength of resisting the shear deformation. The computed bulk moduli ofPnma-TiB,Cmcm-TiB andPmmm-TiB can reach 205.73 GPa,518.98 GPa and 586.28 GPa, respectively, which are comparable to those ofα-TiB2(268 GPa)andβ-TiB2(267 GPa).[33]Interestingly, the obtained shear modulusGofPnma-TiB is about 191.58 GPa at ambient pressure, close to that ofα-BeB6(227 GPa),[15]which implies thatPnma-TiB may also be a hard material. In addition, the obtained Young’s moduli forPnma-TiB,Cmcm-TiB andPmmm-TiB are 438.59 GPa,736.68 GPa and 655.86 GPa, which are larger than 400 GPa,suggesting that these three crystals have strong stiffness. We can judge the ductility or brittleness of a material by theB/Gratio. Usually, ifB/G >1.75, the material is ductile, other wise it is brittle.[71]TheB/GofPnma-TiB,Cmcm-TiB, andPmmm-TiB is 1.07, 1.78, and 2.34, respectively, demonstrating thatPnma-TiB is ductile, and the other two phases are brittle under different conditions. Poisson’s ratioνis an extremely significant parameter to assess the degree of directionality of the covalent bond. The representative values of 0.1,0.25 and 0.33 correspond to the covalent, ionic and metallic materials, respectively. The derived Poisson’s ratioνfor thePnma-TiB structure is 0.14, close to 0.1, indicating the existence of a strong covalent bond, and this crystal can be classified into the covalent material. TheCmcm-TiB polymorph has the Poisson’s ratioνof 0.27, approaching 0.25, revealing that this structure can be divided into the ionic material.The calculated Poisson’s ratioνfor thePmmm-TiB is exactly equal to 0.33, which can be deemed as the metallic material.Subsequently,the Vickers hardness values for these three configurations were predicted with an empirical model suggested by Chenet al.,[58]which are also summarized in Table 2.In Table 2, it is clearly found that the hardness of thePnma-TiB phase is 36.81 GPa, which is comparable to the experimental result ofβ-SiC (34 GPa)[72]and the theoretical values oftP40 carbon (40.2 GPa)[73]and ScB3(38.3 GPa),[63]suggesting a potential hard material. More importantly, theCmcm-TiB phase at 100 GPa and thePmmm-TiB structure at 140 GPa possess the hardness of 25.17 GPa and 15.36 GPa,respectively,which are higher than that of GaN(15.1 GPa).[72,74]The above results exhibit that both of the high-pressure crystals are potential hard materials.

Table 2. The calculated elastic constants Cij (GPa),bulk modulus B(GPa),shear modulus G(GPa),B/G,Young’s modulus E (GPa),Poisson’s ratio ν and Vickers hardness Hv (GPa)of TiB for the Pnma phase at 1 atm,the Cmcm phase at 100 GPa and the Pmmm phase at 140 GPa.
3.4. Electronic properties and bonding features under high pressure
The electronic properties were explored by the overall calculations of the electronic band structure and densities of states (DOS) forPnma-TiB,Cmcm-TiB, andPmmm-TiB at different pressures,as depicted in Fig.4. The overlap between the conduction and the valence bands of the three structures indicates that all three phases are metallic. In addition, the finite electronic DOS at the Fermi level further confirms the metallic nature of these three structures. For the three phases,the total densities of states (TDOS) near the Fermi level are dominated by Ti-3d states, suggesting that the Ti-3d orbital plays a dominant role in their metallicity. At the same time,there is strong hybridization between Ti-3d and B-2p bands in the valence region. Hence,the strong covalent bonds between Ti and B atoms are present.
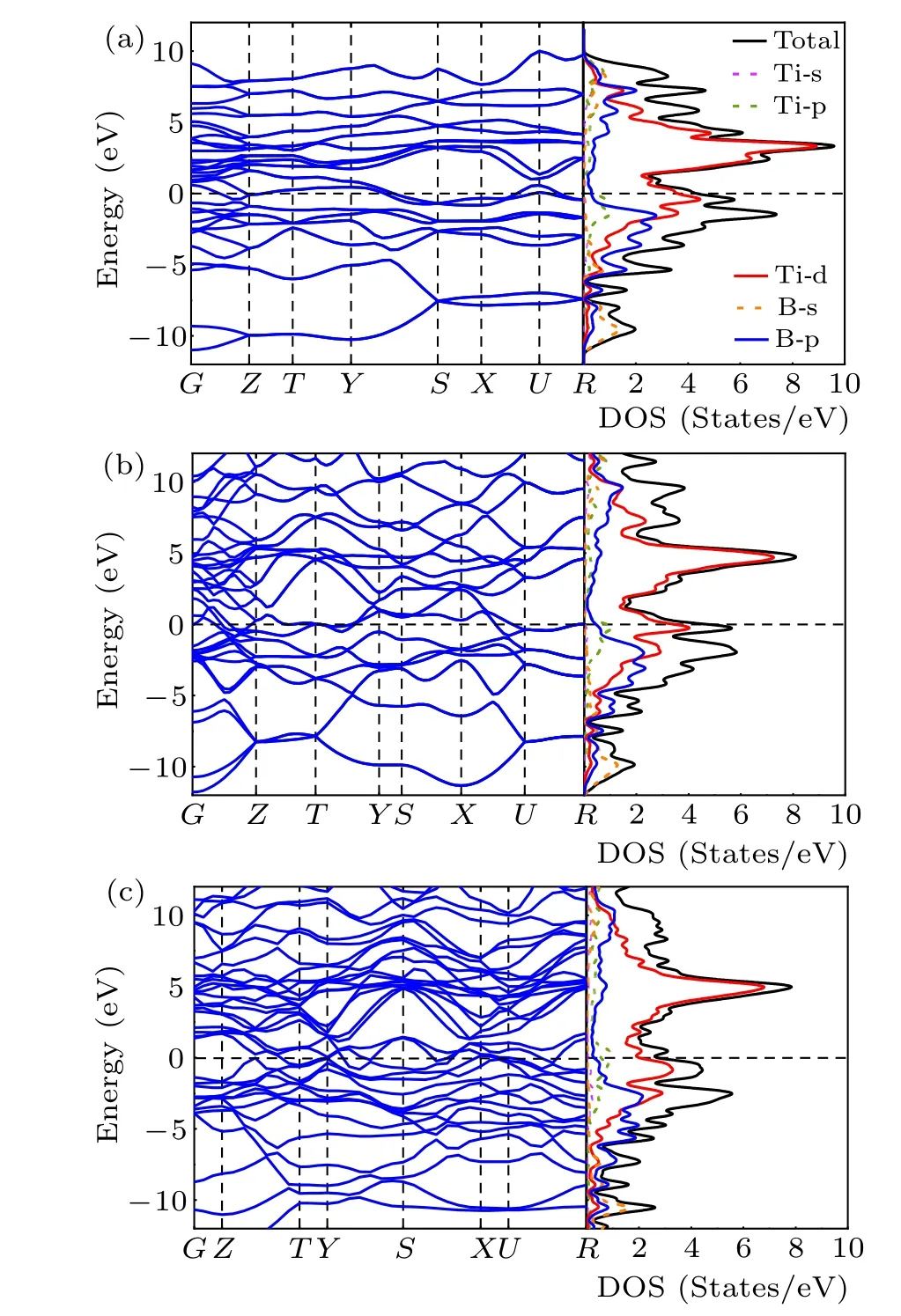
Fig.4. Electronic band structures and densities of states for(a)Pnma-TiB at 1 atm, (b) Cmcm-TiB at 100 GPa and (c) Pmmm-TiB at 140 GPa. The Fermi level is set to zero.
To further reveal the bonding nature ofPnma-TiB at 1 atm,Cmcm-TiB at 100 GPa,andPmmm-TiB at 140 GPa,we computed their electron local functions (ELFs), as presented in Fig.5. The ELF is generally used to describe the chemical bonding with the ELF value range of 0–1. The large ELF values (>0.5) correspond to the lone electron pairs or covalent bonds while the typical ELF value of 0.5 corresponds to homogeneous free-electron gas.[75,76]In Fig.5,the high ELF values exists between B and B atoms,demonstrating the existence of strong B–B covalent bonding within the zigzag chain and the planer six-membered cycle in these three phases. Between Ti and B atoms,ELF exhibits relatively large values close to the B position, revealing the Ti–B covalent interaction. To further verify the feature of the covalent bonding in TiB,we calculated the crystal orbital Hamilton population (COHP) and the integral crystal orbital Hamilton population (ICOHP) of Ti–B and B–B. As displayed in Fig. 6, the obtained COHPs indicate that the Ti–B and B–B bonds both possess the covalent bond features. The ICOHP values of the B–B pairs inPnma-TiB (-5.96 eV),Cmcm-TiB (-6.79 eV), andPmmm-TiB (-7.44 eV), which are comparable to that for the B–B pair(-7.72 eV[58])inα-B,reveal strong B–B covalent bonds.The ICOHP values of the Ti–B pairs inPnma-TiB,Cmcm-TiB,andPmmm-TiB are-1.76 eV,-2.30 eV and-2.38 eV,respectively, which are smaller than those of the corresponding B–B pairs. The above results confirm that the B–B bonds have stronger covalent bonding than the Ti–B bonds in these three structures. In addition,the excellent mechanical properties may stem from the strong covalent bonds of Ti–B and B–B. Overall, we conclude that the chemical bonds in the three TiB phases contain a combination of the strong Ti–B and B–B covalent bonds,which is the major reason for their high elastic modulus and Vickers hardness.
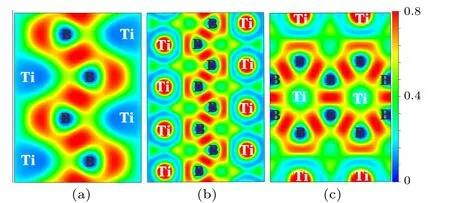
Fig.5. ELF of three TiB phases: (a)(100)plane for the Pnma-TiB at 1 atm,(b) (100) plane for the Cmcm-TiB at 100 GPa and (c) (010) plane for the Pmmm-TiB at 140 GPa.

Fig. 6. The COHP curves for (a) Pnma-TiB at 1 atm, (b) Cmcm-TiB at 100 GPa and (c) Pmmm-TiB at 140 GPa. The dotted vertical line at 0 eV represents the Fermi energy level.
4. Conclusions
Based on the particle swarm optimization CALYPSO method for structure prediction in conjunction with firstprinciples calculations, we explored the phases of TiB within the pressure range of 0–200 GPa. The phase transition sequence ofPnma →Cmcm →Pmmmhas been established under high pressure and the transition pressures were determined as 69.08 GPa and 110.88 GPa, respectively. A novel orthorhombicPmmmwas firstly uncovered under high pressure.Intriguingly, accompanied by the phase transition, the evolution of the boron framework is from a one-dimensional zigzag chain inPnma-TiB andCmcm-TiB to a graphene-like B-sheet inPmmm-TiB. This planar B-sheet was firstly reported in transition-metal monoborides. Phonon spectrum and elastic constant calculations show that these three configurations are dynamically and mechanically stable.According to an empirical hardness model,the Vickers hardness values ofPnma-TiB,Cmcm-TiB, andPmmm-TiB are estimated to be 36.81 GPa,25.17 GPa and 15.36 GPa,respectively,stating that these three phases are promising hard materials. The results of electronic band structure and density of states show that the three TiB polymorphs possess metallic properties. Further analysis of the computed density of states, electron localization function and COHP indicates a combination of the strong B–B and Ti–B covalent bonds in three TiB crystals. This particular bonding feature is mainly responsible for their high elastic modulus and Vickers hardness. The present work expands the knowledge about the pressure-induced phase transition and boron framework evolution for transition-metal monoborides,which inspires experimental efforts in the synthesis.
Data availability statement
The data that support the findings of this study are openly available in Science Data Bank at https://www.doi.org/10.57760/sciencedb.j00113.00063
Acknowledgements
This work was supported by the National Natural Science Foundation of China(Grant No.11804031),the Scientific Research Project of Education Department of Hubei Province,China(Grant No.Q20191301), Youth Science Foundation of Jiangxi Province, China (Grant No. 20171BAB211009), and Henan Province Key Research and Development and Promotion of Special Scientific and Technological Research Project(Grant No.222102320283).
- Chinese Physics B的其它文章
- A design of resonant cavity with an improved coupling-adjusting mechanism for the W-band EPR spectrometer
- Photoreflectance system based on vacuum ultraviolet laser at 177.3 nm
- Topological photonic states in gyromagnetic photonic crystals:Physics,properties,and applications
- Structure of continuous matrix product operator for transverse field Ising model: An analytic and numerical study
- Riemann–Hilbert approach and N double-pole solutions for a nonlinear Schr¨odinger-type equation
- Diffusion dynamics in branched spherical structure

