Micro-vibration response analysis and its application of electronic workshop raw land based on whale optimization algorithm
YU Caizhi, LU Yutai, WANG Peng, SUN Changku
(State Key Laboratory of Precision Measuring Technology and Instruments, Tianjin University, Tianjin 300072, China)
Abstract: Environmental micro-vibration is one of the key factors impacting the running of electronic workshop. Low frequency micro-vibration has a significant influence on the normal operation of high precision machining and testing equipment, and even causes irreversible damage to the equipment. Micro-vibration testing and response analysis are important to guide the vibration isolation design and ensure the stable operation of various precision equipment in the workshop. Parameters of Davidenkov model are fitted based on whale swarm optimization algorithm, and its applicability is verified. At the same time, taking the testing project of an electronic workshop raw land as an example, the micro-vibration response is analyzed. The results show that the nonlinear constitutive model constructed by whale optimization algorithm can simulate the dynamic nonlinear behavior of soil under the action of micro-vibration better. Compared with the traditional equivalent linearization method, the nonlinear constitutive model based on the whale optimization algorithm has a smaller acceleration response value. It can effectively suppress the “virtual resonance effect” produced by the equivalent linearization method.
Key words: micro-vibration response; nonlinear dynamic constitutive model; whale optimization algorithm; electronic workshop raw land
0 Introduction
With the rapid growth in the field of microelectronics production and testing, industrial manufacturing is increasingly developing in the direction of high precision and ultra-high precision. And the demand for high-precision electronic industrial plants (microelectronics, optical instruments, lasers, nanomaterials, etc.) is on the rise[1]. With a large number of semiconductor production test apparatuses introduced into actual production, such as czochralski growth furnace, polishing machine, photoetching machine and scanning electron microscope etc., the more expansive production scale, the more complex structure of processing components, and the higher requirements for processing accuracy follow[2]. The high-precision electronic industrial workshops have more stringent requirements for environmental micro-vibration[3], and thus the design of anti-mircovibration is essential to ensure the normal use of precision instruments in electronic factories.
The equivalent linear or nonlinear constitutive model is used to simulate the dynamic response of environmental micro-vibration. However, due to the difficulty in defining model parameters and the large amount of calculation of nonlinear constitutive model, equivalent linear iterative method is usually employed to approach the real nonlinear constitutive model in the actual construction of soil dynamic response constitutive model[4]. However, due to the significant error in calculating the high frequency part of the equivalent linearization method, the movements of soil cannot be truly reflected, resulting in obvious resonance, which leads to the overestimation of micro-vibration response and limits the further development of equivalent linearization methods[5]. Compared with other nonlinear constitutive models, Davidenkov model has a relatively simple expression and a good fitting effect on the nonlinear behavior of soil. Davidenkov model is widely used in actual production.
In order to explore the application of Davidenkov model in analyzing environmental micro-vibration response, the parameters of Davidenkov’s model are fitted based on whale optimization algorithm, and Matlab are used to compile the fitting curve algorithm. Finally, the fitting effect of the algorithm is verified by the corresponding experimental data. UMAT, the secondary development platform provided by ABAQUS, is used to write the viscoelastic model subroutine of soil. In this paper, a soil structure simulation model is established based on the raw land test project of an electronic workshop. In order to provide reference for anti-vibration design of high precision electronic workshop, the environmental micro-vibration response is analyzed.
1 Theoretical method
1.1 Equivalent linear model
The equivalent linear model is based on the viscoelastic theory. It adopts Kelvin-voigt model to reflect the hysteretic characteristics of soil under cyclic loading[6]. Kelvin-voigt model consists of a linear elastic spring and a sticky pot in parallel, and its stress-strain relationship is defined as
τ=Gγ+ηGγ′,
(1)
whereGis shear modulus;ηGis shear viscosity coefficient, andτis shear stress. Shear viscosity coefficient is defined as
ηG=2Gλ/ω,
(2)
whereλis the damping ratio, andωis the circular frequency.
Considering the stress-strain relationship in three-dimensional state, Eq.(1) can be generalized as

(3)
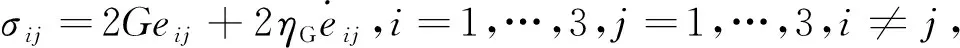
(4)
whereKis the volume modulus of the material, andηKis the coefficient of viscosity of volume. The coefficient of viscosity of volume is defined as
ηK=2Kλ/ω.
(5)
According to the analysis, the subroutine of the equivalent linear viscoelastic model is written by UMAT.
1.2 Theoretical formulas
The dynamic shear modulus ratio is defined as[7]
G/Gmax=1-H(γ),
(6)
whereH(γ) is defined as
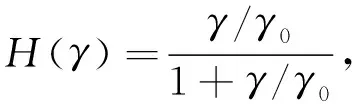
(7)
whereGmaxis the maximum shear modulus;γis shear strain amplitude, andγ0is reference shear strain. Based on Davidenkov model, Eq.(7) can be rewrote as[8]
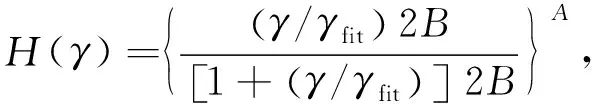
(8)
whereA,Bandγfitare fitting parameters related to soil properties.
The damping ratio is defined as[7]
λ=λmax(1-G/Gmax)n,
(9)
whereλis damping ratio;λmaxis the maximum damping ratio, andnis fitting parameters.
Through a large number of dynamic shear experiments on soil, the damping ratio is defined as[9]
λ=λmin+λ0(1-G/Gmax)n,
(10)
whereλ0,nare fitting parameters, andλminis the minimum damping ratio of soil corresponding to the initial dynamic shear modulus.
1.3 Fitting of soil parameters
The characteristics of shear modulus and damping ratio of soil with shear strain are related to the fitting parametersA,Bandγfitin Eq.(8). There are optimization methods such as Newton’s method, gradient descent and the conjugate gradient method to solve the problem of parameter fitting. However, these methods have some defects, such as a large amount of calculation, want of gradient information and unsatisfactory fitting effects concerning high-dimensional complex functions. In this paper, whale optimization algorithm is introduced to fit parameters. It has higher accuracy and optimization speed when fitting parameters of nonlinear complex functions.
Whale optimization algorithm[10]is proposed according to the predation behavior of humpback whales. It is divided into three stages which are encirclement stage, development stage and exploration stage.
1.3.1 Encirclement stage
To simulate the behavior of humpback whales surrounding their prey, Mirjalili came up with the formulas as
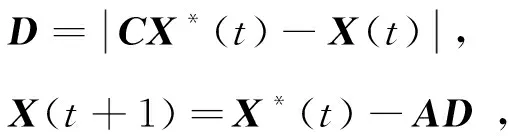
(11)
whereX*is the position vector of the current optimal solution;tis the number of current iterations;Xis the position vector, andAandCare the coefficient vectors.
1.3.2 Development stage
Humpback whales hunt their prey in spiraling motion which corresponds to the development stage in the algorithm. Mirjalili came up with the formula as
X(t+1)=D′e(bl)cos(2πl(wèi))+X*(t),
(12)
whereD′=|X*(t)-X(t)| is the best solution currently obtained;bis a constant that defines the shape of a logarithmic spiral, andlis a random constant in [-1,1]. In addition, whales also shrink their enclosure as they spiral to simulate this behavior. Assuming that there is a probability constantpibetween the spiral model and the contract-enveloping mechanism, so that the position vector of the best solution during optimization is constantly update. It is defined as
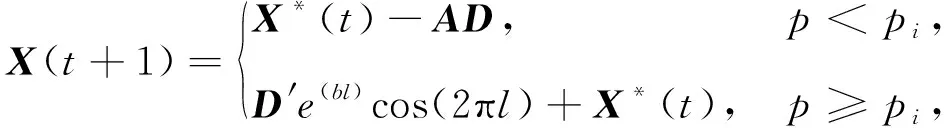
(13)
wherepis a random constant in [0,1].
1.3.3 Exploration stage
Mirjalili simulated the random hunting behavior of whales to improve the global searching ability of the algorithm. Mirjalili came up with the formulas as
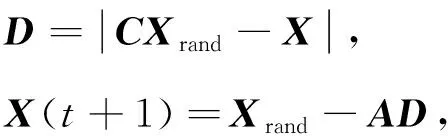
(14)
whereXrandis the position of the randomly selected solution vector. When |A|<1, the optimal solution vector in the current iteration is updated to the position of other solution vectors. When |A|≥1, a random solution vector is used to update the position information of other solution vectors.
The normalized cross correlation[11]is introduced to verify the similarity between measured data and fitted data. It is defined as
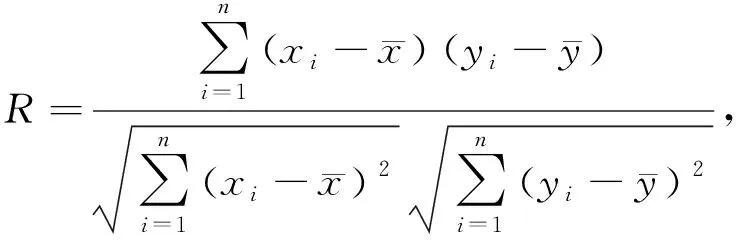
(15)
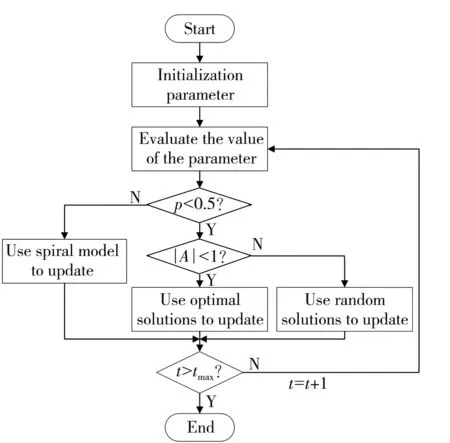
Fig.1 Flow chart of whale optimization algorithm
To verify the accuracy and feasibility of the fitting algorithm, the parameters of the formula of dynamic shear modulus ratio and damping ratio in Davidenkov model of various soils are fitted. Table 1 shows the dynamic structure test data of various soils selected[12-14].
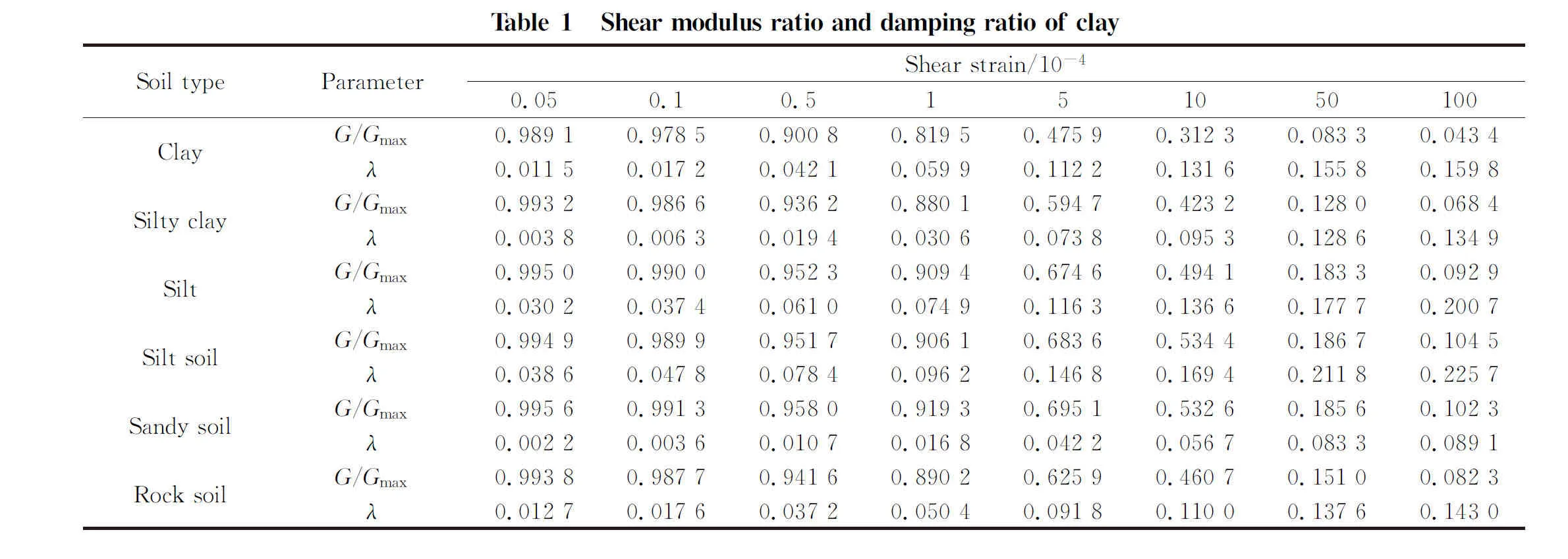
The fitting curves of various soils are shown in Fig.2.
Table 2 presents parameter fitting results andRvalues of Davidenkov model. The results show that the whale optimization algorithm has good fitting effect.
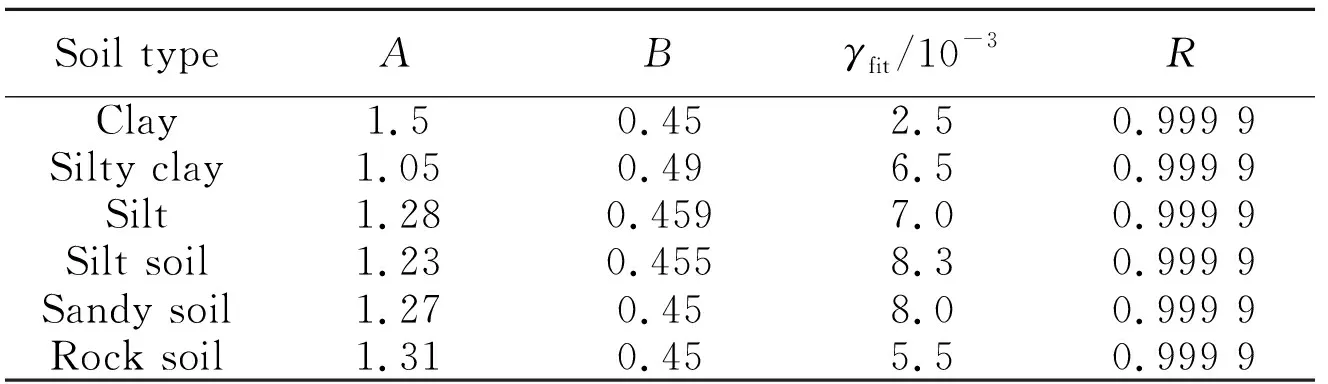
Table 2 Fitting results of different soil types
2 Creation of models
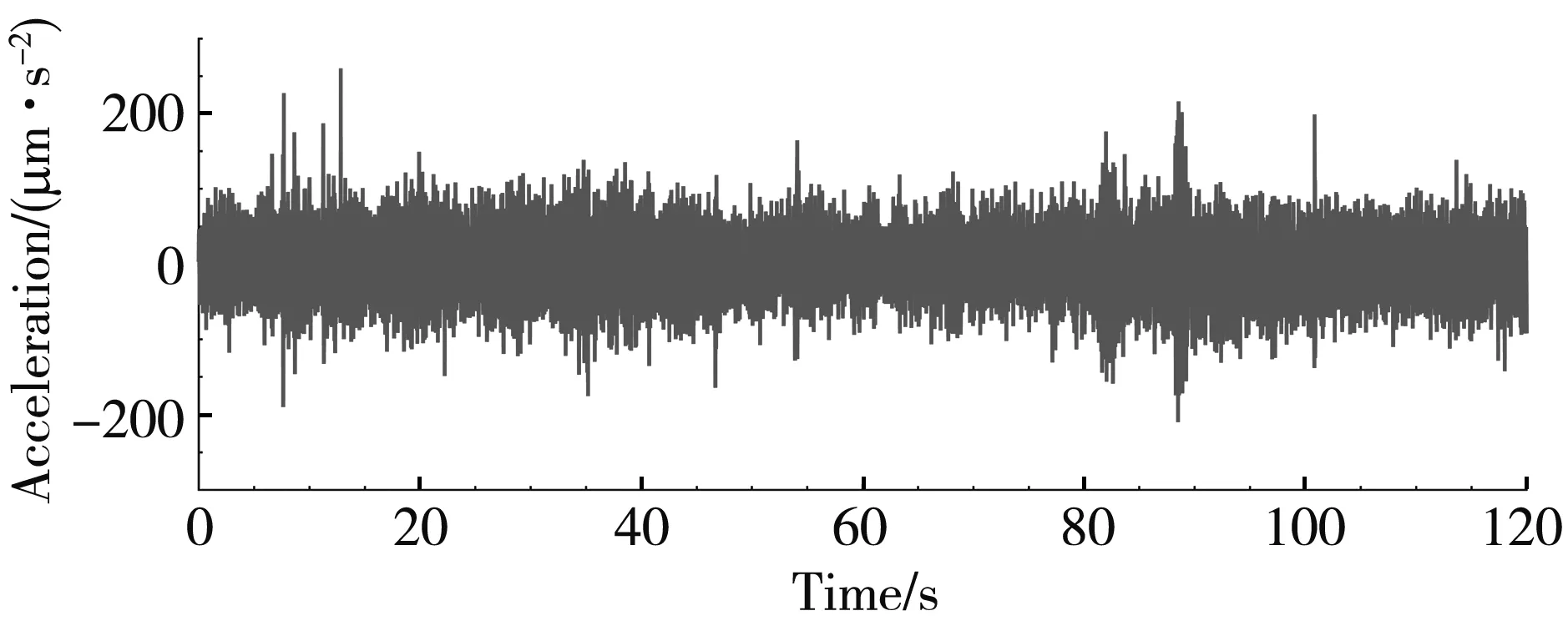
A site vibration survey is carried out on the electronic workshop raw land, and its baseline vibration levels is quantified. The survey included a series of tri-axial ambient vibration measurements at selected locations on the proposed site. The accelerometers are placed atop a spike deeply hammered into the soil, so that they can effectively detect vibrations propagated along the soil surface in form of Rayleigh waves. The typical site vibration data acquired on site is shown in Fig.3.
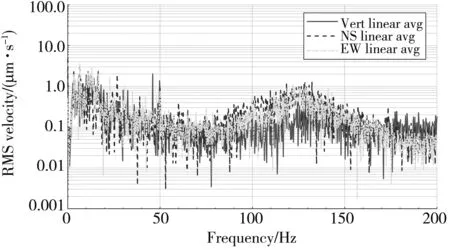
Fig.3 Typical site vibration data acquired on site
According to geotechnicalengineering reports, the laboratory site for the test project is fairly flat. Therefore, the terrain details are not specified in the model. The building scale is relatively small (138 m×58 m). The soil layers of the whole site are basically the same.
The soil stratification of site is presented as Table 3.

Table 3 Soil stratification in site
The overall size of the soil model is 200 m×200 m×30 m, large enough to cover the building and its proximity. The element dimension is chosen as 4 m×4 m×2 m, optimized to characterize the Rayleigh wave motions between 4 Hz and 10 Hz. The mat slab, made of C30 concrete, is placed at the depth of 2 m in the middle. Its elastic modulus is 3×104MPa, density is 2 500 kg/m3, and Poisson’s ratio is 0.3. The data of dynamic shear modulus, dynamic shear strain and damping ratio of each layer of soil are from the experimental data[12-14]provided in literatures. According to the proposed fitting method, the dynamic structure characteristic curves of each layer of soil can be obtained. The fitting curves are shown in Fig.4.
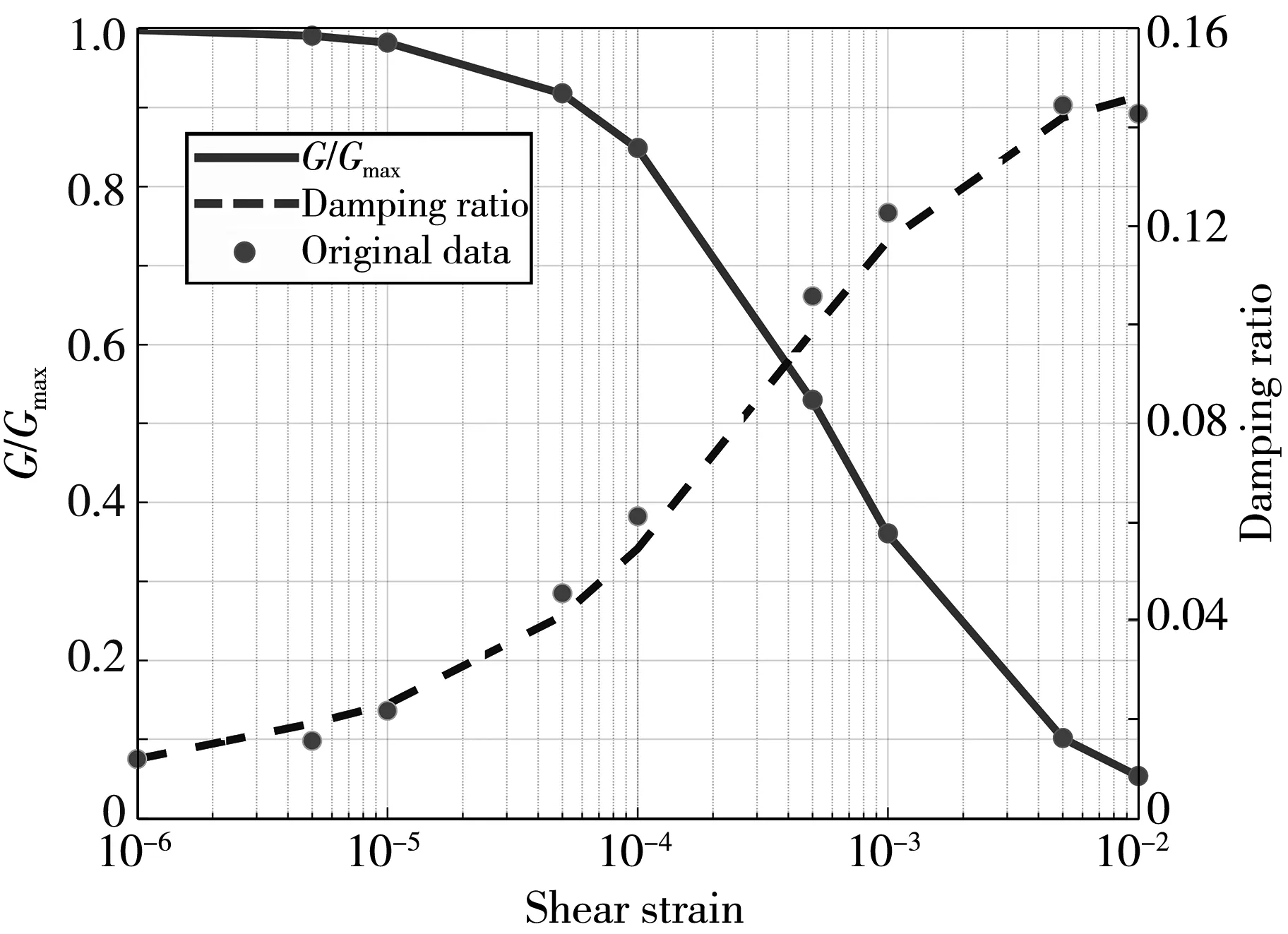
(a) Soil infill
In order to facilitate the calculation of equivalent linear viscoelastic constitutive model and avoid the hourglass phenomenon caused by reducing integral units, C3D8 element (three-dimensional solid integral element) is adopted for soil and mat slab structure. Damping can directly affect the calculation accuracy of the model. The damping of the soil model is Rayleigh damping[15]. Rayleigh damping can be calculated by taking the natural frequencies of the two modes through modal analysis. Generally, the first mode and the fourth mode are selected as shown in Table 4.
In order to simulate the propagation characteristics of micro-vibration in infinite domain foundation, the viscoelastic boundary should be set around the soil model[16]. Viscoelastic artificial boundary is a system composed of springs and dampers. The mechanical parameters of springs and dampers are related to the properties of rock and soil materials. It is defined as
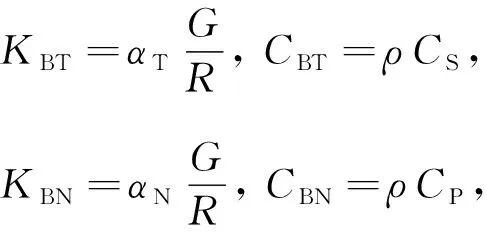
(16)
whereKBTandKBNare the normal and tangential stiffness of spring respectively;Ris the distance between wave source and artificial boundary point;Gis the shear modulus of the medium;ρis mass density of the medium;αTandαNare tangential and normal viscoelastic artificial boundary parameters, respectively;CSandCPare transverse wave and longitudinal wave velocities, respectively. Tangential and normal viscoelastic artificial boundary parametersαTandαNare 0.67 and 1.33, respectively. Table 4 shows additional soil parameters for each layer of soil from geotechnical engineering reports.
The soil finite element model finally established is shown in Fig.5, where the measuring point is the experimental observation position.
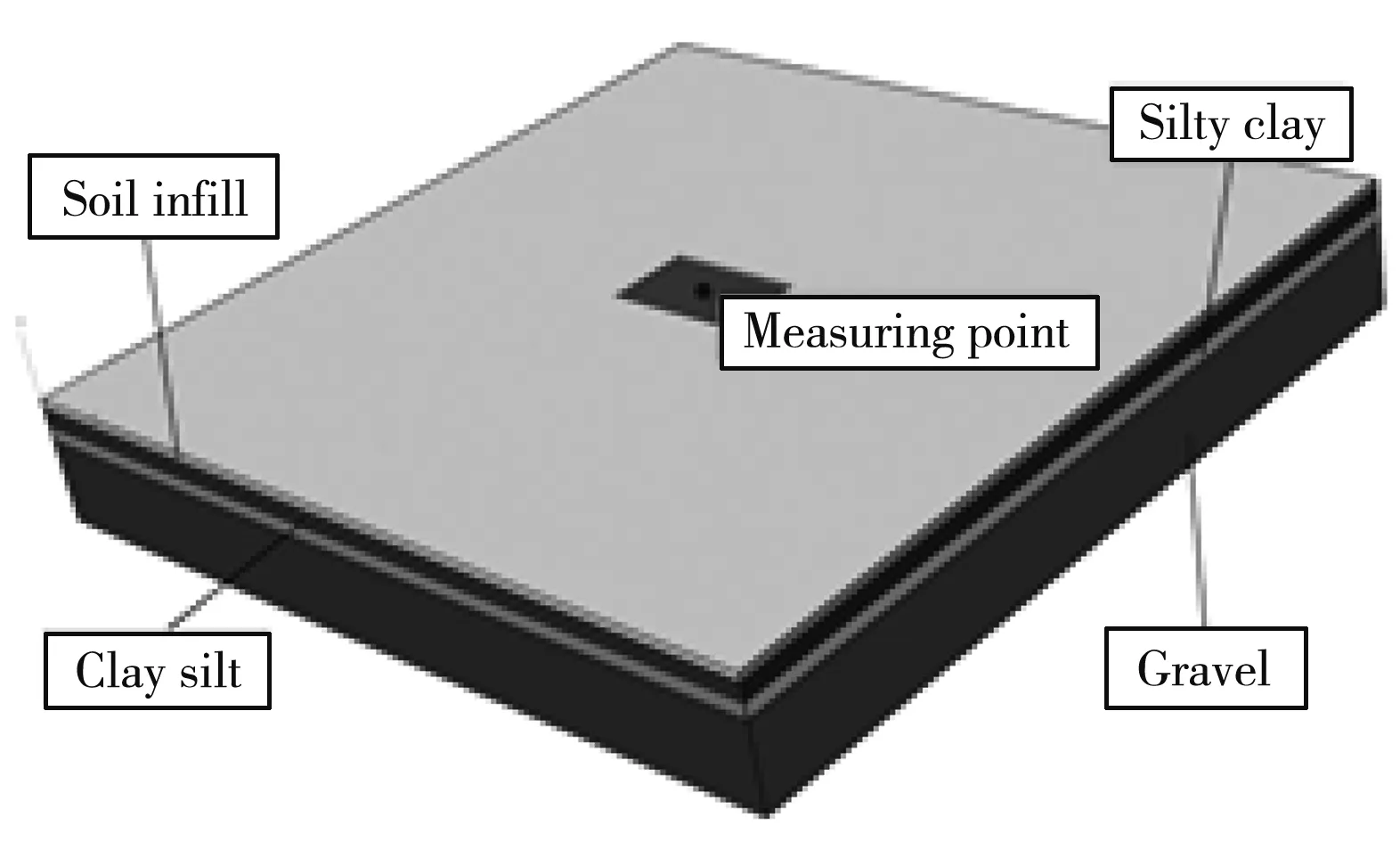
Fig.5 Finite element model of soil
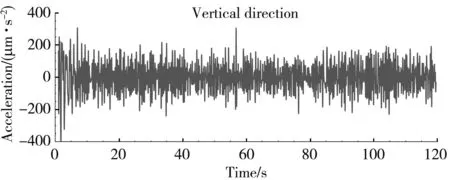
The measured data of the site environment (Fig.6) is applied to the bottom of the model as the input excitation load.
(a) Vertical direction
Assuming an initial damping ratio and shear modulus, the maximum shear strain experienced by each element during the calculation process is recorded. The shear modulus and damping ratio are calculated according to the new material parameters. The whole process is repeated several times until the material properties no longer change. The inelastic and nonlinear properties of the real soil are continuously approximated by this method of multiple iterative fitting.
3 Results and discussion
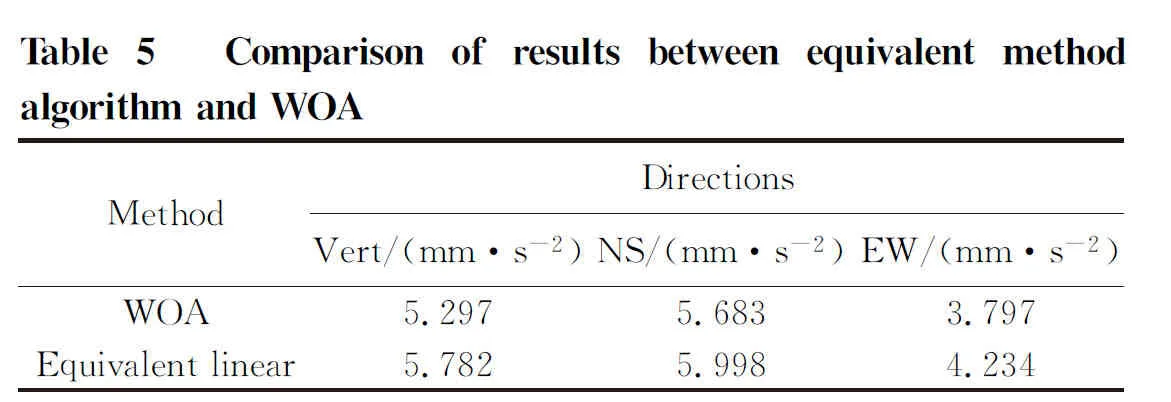
The stress change of the backing plate under the action of environmental micro-vibration is obtained by using ABAQUS to carry out numerical calculation. The time-history curves of acceleration at monitoring points obtained by the two methods are shown in Fig.7. The comparison results of the two methods are presented as Table 5. The peak value of acceleration response in three directions calculated by equivalent linearization method are all larger than those of the algorithm in this paper. This is mainly due to the “virtual resonance effect” produced by the equivalent linearization method, which overestimates the micro-vibration responses.
(a) Whale swarm optimization algorithm
Under the action of micro-vibration signals, the peak accelerations in each direction of the observation point are slightly different. Compared with the equivalent linear method, the peak value of acceleration response in three directions obtained by the proposed fitting method is smaller.It is due to the “virtual resonance effect” generated by the equivalent linearization method, which overestimates the micro-vibration responses in each direction. The attenuation factor of the mat slab at various thicknesses can be calculated. The baseline site vibrations meet VC-D as shown in Fig.8.

Fig.8 Tridirectional spectrum diagram
Thus, when subjected to traffic/mechanical vibrations from nearby roads and buildings, a slab thickness of 1 200 mm will be sufficient to ensure a VC-D (or even better) environment on the pads.
4 Conclusions
1) Parameters of Davidenkov model are fitted based on whale algorithm, and the fitting effect is verified by dynamic structure test data of various soils. The whale swarm optimization algorithm has a good fitting effect on the parameters of Davidenkov model, and the normalized cross correlation (NCC) coefficient of various soils is close to 1.
2) Taking araw land test project of an electronic workshop as an example, the calculation results of nonlinear constitutive model of soil is analyzed based on whale swarm optimization algorithm and equivalent linearization method. It is concluded that the nonlinear constitutive model based on the whale optimization algorithm has a smaller acceleration response than the equivalent linearization method. The “virtual resonance effect” produced by the equivalent linearization method is effectively suppressed to prevent overestimation of micro-vibration responses.
3) From the simulation analysis of micro-vibration response of an electronicworkshop, a conclusion is drawn that the nonlinear constitutive model constructed by whale optimization algorithm can describe the dynamic nonlinear behavior of soil under the action of micro-vibration. The acceleration response obtained by the simulation analysis conforms to the general law and meets the design requirements, which is suitable for the analysis and study of the micro-vibration response of electronic workshop.
 Journal of Measurement Science and Instrumentation2022年4期
Journal of Measurement Science and Instrumentation2022年4期
- Journal of Measurement Science and Instrumentation的其它文章
- Model predictive flux control of permanent magnet synchronous motor driven by three-level inverter based on fine-division strategy
- An FPGA-based LDPC decoder with optimized scale factor of NMS decoding algorithm
- Parameter matching of hydraulic balancing circuit based on AMESim
- Analysis of safety characteristics of coal-based aviation kerosene
- Fabrication and stiffness optimization of carbon-based composite double polymer compliant electrode
- An evolutionary game based security decision algorithm for wireless sensor networks
