Biophysical neurons, energy, and synapse controllability: a review
Jun MA
Reviews
Biophysical neurons, energy, and synapse controllability: a review

1Department of Physics, Lanzhou University of Technology, Lanzhou 730050, China2School of Science, Chongqing University of Posts and Telecommunications, Chongqing 430065, China
Diffusive intracellular and extracellular ions induce a gradient electromagnetic field that regulates membrane potential, and energy injection from external stimuli breaks the energy balance between the magnetic and electric fields in a cell. Indeed, any activation of biophysical function and self-adaption of biological neurons may be dependent on energy flow, and synapse connection is controlled to reach energy balance between neurons. When more neurons are clustered and gathered closely, field energy is exchanged and shape formation is induced to achieve local energy balance. As a result, the coexistence of multiple firing modes in neural activities is fostered to prevent the occurrence of bursting synchronization and seizure. In this review, a variety of biophysical neuron models are presented and explained in terms of their physical aspects, and the controllability of functional synapses, formation of heterogeneity, and defects are clarified for knowing the synchronization stability and cooperation between functional regions. These models and findings are summarized to provide new insights into nonlinear physics and computational neuroscience.
Energy balance; Creation of synapse; Functional neuron; Heterogeneity; Defects
1 Introduction
Decision-making in the nervous system controls the motion and gait of animals and human, and it depends on cooperation and competition between neurons, both within the same functional region and in other regions of the brain. The application of magnetic resonance imaging technology (MRIT) (Geethanath and Vaughan, 2019) provides helpful evidence for building a functional brain network (Davison et al., 2015; Fraschini et al., 2016; Telesford et al., 2016; Vecchio et al., 2017) and for exploring the neural activities and occurrence mechanisms in defects and abnormalities of the brain. Some results are helpful for discovering the working mechanisms and applying appropriate schemes which can cure nervous diseases (He and Yao, 2020; Shi et al., 2020; Yang and Sawan, 2020; Ahmad et al., 2022; Yan et al., 2022). In the nervous system, biological neurons (Manor and Nadim, 2001; Mishra et al., 2006; Grassia et al., 2011; Bailoul and Alaa, 2020; Nasiraee et al., 2022) have the main role in signal exchange and information encoding, and more evidence have confirmed the contribution from astrocytes (Ricci et al., 2009; Brekke et al., 2015; Durkee and Araque, 2019; Khakh, 2019; Bonvento and Bola?os, 2021). It appears that astrocytes regulate calcium flow, which can effectively adjust muscle contraction and heartbeat (Silverman et al., 2006; Calabrese et al., 2016; Giuriato et al., 2020; Kuhtz-Buschbeck et al., 2021). There is a distinct difference between biological neurons and generic neuron models, although both of them can estimate and predict the mode of transition in neural activities. Indeed, the effect of ion channels becomes very important in discerning mode selection and pattern development; this allows the propagation of calcium, potassium, and sodium along membrane channels to be better addressed.
On the other hand, special anatomic structure should be considered with regard to signal processing and control of neural activities. For example, cable neuron models (Tuckwell, 2006; Elbasiouny, 2014; Guo et al., 2016; Latorre and W?rdell, 2019) can describe signal propagation along an axon. Wang et al. (2017) mentioned that the formation of autapses on some interneurons results from injury to the axon, and an auxiliary loop is then created to correct signal propagation. Autaptic driving can be excitatory or inhibitory (Song et al., 2019; Yao et al., 2019; Zhao et al., 2020; Wu et al., 2021; Qi et al., 2022), and based on what type of autaptic current it generates, it is classified as an electrical or chemical autapse. With regard to dynamics, when an autapse connects to a neuron it simply applies time-delayed feedback to the membrane potential, and the normalized parameters can be tamed to control the firing modes and pattern. In a neural network, local distribution of inhibitory autapses can promote development of defects that block wave propagation (Qin et al., 2015), while a local excitatory autapse can induce heterogeneity for emitting wave fronts (Ma et al., 2015a, 2015b; Yilmaz et al., 2016; Protachevicz et al., 2020; Baysal et al., 2021). Indeed, activation of an autapse can enhance the self-adaption of neurons for selecting suitable firing modes and protect them from electromagnetic radiation (EM) (Ren et al., 2017; Xu et al., 2017; Ge et al., 2019, 2021; Njitacke et al., 2022).
A model approach for neurons should mainly consider biophysical properties during the generation of neural activities and action potentials. Mathematically, discrete model and maps can reproduce the mode selection in neural activities (Hemby et al., 2002; Ibarz et al., 2008; Bashkirtseva et al., 2018; Nouri et al., 2019; Muni et al., 2022), and they are more suitable for realization of digital circuits via field programmable gate array (FPGA) (Graas et al., 2004; Matsubara et al., 2011; Nazari et al., 2015; Malik and Mir, 2020). Differential-equation?–?based neuron models are helpful for predicting mode selection and transition in electric activities, and the effect of electromagnetic induction can be estimated by introducing the magnetic flux variable (Wu et al., 2017; Baysal and Yilmaz, 2020; Kafraj et al., 2020; Yuan et al., 2020; Upadhyay et al., 2022). Fractional-order neuron models are helpful to show the memory effect and non-diffusive properties in neurons (Shi and Wang, 2014; Teka et al., 2018; Chen et al., 2019; Mondal et al., 2019; AbdelAty et al., 2022). In fact, reliable neuron models are critical in discerning the collective behaviors of neural networks; once this is accomplished one can understand controllability in synapses, biophysical effects during occurrence of action potentials, noisy disturbance and electromagnetic radiation, energy exchange, and wave propagation in the nervous system. For previous discussion and suggestions, readers can find explanations and possible guidance in these reviews and the references therein (van Geit et al., 2008; Ma and Tang, 2017; Wang and Ma, 2018; Ma J et al., 2019; Wang CN et al., 2019; Lin et al., 2021; Ma, 2022).
In this review, we primarily introduce the functional synapse, some biophysical neurons and their energy role in controlling firing modes and growth of synapses, and formation of heterogeneity and defects in neurons and networks. As is well known, some nonlinear circuits can be tamed to reproduce the main dynamical properties of biological neurons, and thus more neural circuits are obtained to develop reliable physical neuron models, which exhibit stronger synaptic function due to enhancement of the biophysical properties of channels.
For simplicity, we will use a simple neural circuit (Kyprianidis et al., 2012) composed of one capacitor, inductor, nonlinear resistor, constant voltage source, and external forcing source to clarify some physical properties of the neural circuit, and obtain different functional neuron models from this. The neural circuit, driven by a time-varying voltage sources, is presented in Fig. 1.
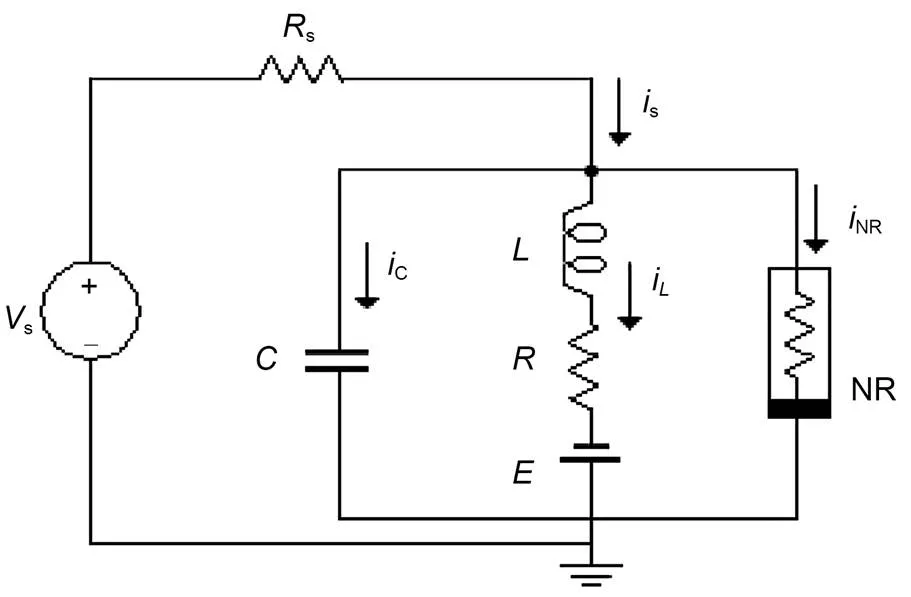
Fig. 1 Schematic diagram of a resistor-inductor-capacitor (RLC) neural circuit. NR is a nonlinear resistor and E denotes a constant voltage expressing the reverse potential in the ion channel. Rs and R are ideal linear resistors, and C and L represent the capacitor and inductor, respectively. Vs denotes a periodic voltage source. i is the current
In practice, the external stimulus can be selected as a voltage source, piezoelectric ceramic part, phototube, or even output end from another nonlinear circuit, and then the neural circuit can be excited to generate different firing patterns. The circuit equations for Fig. 1 can be obtained by
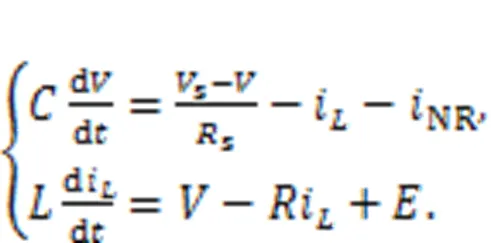
The channel current across the nonlinear resistor NR can be approached by
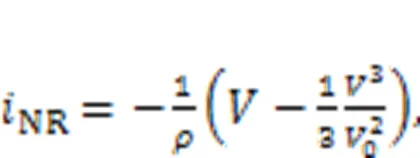
wheredenotes the voltage across the nonlinear resistor and equals the output voltage from the capacitor, and the parametersand0represent the dimensionless conductance and inverse voltage for the nonlinear resistor, respectively. In addition, the field energy (FE) in this neural circuit is defined by
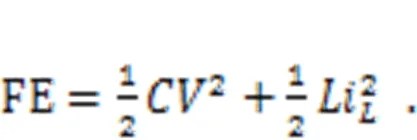
For further nonlinear analysis, the dynamics of the neural circuit is replaced by an equivalent generic neuron model by applying scale transformation to the physical variables and parameters in the circuit equations, as follows:
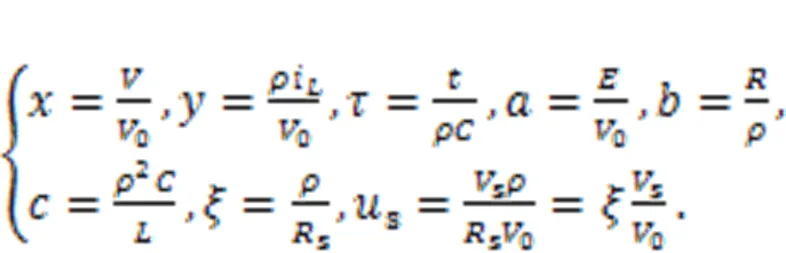
As a result, a simple neuron and its Hamilton energy function are given in
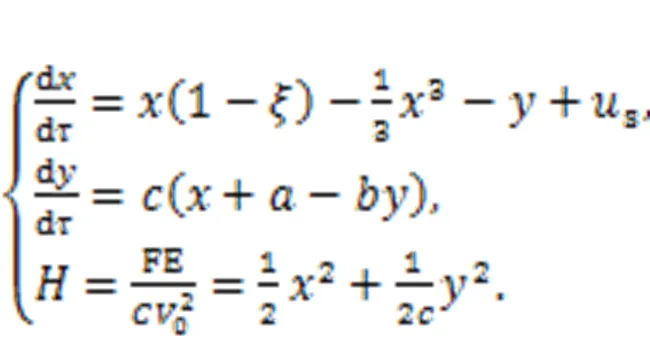
Dynamically speaking, the equivalent external stimulusscan be changed to regulate the firing modes of the neural activities. From a physical viewpoint, electric field energy and magnetic field energy will change the ratio to the total energy when the neuron is excited, and the energy flow will then control the mode selection for the electric activities completely. As a result, external energy injection will break the balance between the magnetic and electric fields in the neuron, and mode transition will be induced as soon as possible. By changing the external stimulus, the neuron is excited to present spiking, bursting, and chaotic states, and it has been found that spiking neurons can exhibit higher energy values, while bursting and chaotic neurons will have lower energy values. Therefore, energy flow is propagated along the coupling channel and the distribution of the neuron's inner field energy is guided to exhibit suitable firing patterns. When more neurons are clustered in the same region, energy flow in each neuron is exchanged and propagated to adjacent neurons to reach the best possible local energy balance, and phase lock occurs when there is field coupling and synaptic coupling among neurons.
2 Enhancement of synapse functions in biophysical neurons
Synapses are important in perceiving external stimuli prior to excitation of biological neurons to produce suitable firing patterns. For two or more neurons, electric and chemical signals are propagated from presynaptic to postsynaptic, accompanied by the generation of an electromagnetic field and exchange of energy flow. Because of the anatomic structure of biological neurons, the cell membrane enables distinct capacitance properties, diffusive ions induce an electromagnetic field, and the channel currents across the cell membrane show clear effects of a magnetic field, which can be associated with the induction coil and functional channels. When ion channels embedded into the cell membrane are activated, more channel currents pass through to change the gradient distribution of intra cellular ions including calcium, sodium, and potassium; then action potential is induced under external stimuli.
When biological neurons are treated as artificial neural circuits, more branch circuits can be applied to estimate the effect of channel currents and physical effects. Therefore, it is important to discuss the realization of these biophysical functions by incorporating specific electric components including memristors (Joglekar and Wolf, 2009; Kim et al., 2015; Corinto and Forti, 2016; Olumodeji and Gottardi, 2017), thermistors (Schmidt et al., 2004; Nenova and Nenov, 2009; Yakovleva et al., 2013; Liu et al., 2018), phototubes (Radziemska and Klugmann, 2002; Hu et al., 2010; Tomimatsu et al., 2022), piezoelectric ceramics (Flynn and Sanders, 2002; Priya et al., 2017; Sugino et al., 2020), and Josephson junctions (Abidi and Chua, 1979; Crotty et al., 2010; Hens et al., 2015; Zhang Y et al., 2020b) into the branch circuits of generic neural circuits; then external physical signals can be perceived and converted into equivalent electric stimuli imposed on the neurons. In addition, these electronic components can be combined to build hybrid synapses for connecting neurons, and field coupling is activated for fast energy exchange, which allows synchronous behaviors to be controlled completely.
2.1 Memristive synapse in biophysical neurons
A memristor is a specific type of electric component whose conductance is dependent on the flow passed through the channel, and the relation between magnetic flux and charges in a memristor can be one of two kinds. When the charge flux is controlled by magnetic fluxas(), a magnetic-flux-controlled memristor is formed, and its memductance is estimated by()=d/d+2, tanh(). For a charge-flux-controlled memristor, the mem-resistance is approached by()=d/d=′+′2, tanh(). For isolate biological neurons, continuous diffusion of intracellular and extracellular ions will induce formation of a changeable electromagnetic field, which has significant impact on the membrane potential and firing modes of neural activity. Inspired by the scheme for a memristive neuron model designed by Lv et al. (2016), which can estimate electromagnetic induction, a magnetic flux variable is usually applied to the neuron model and induction current is used to control the membrane potential. By applying a similar memristive function (Lv et al., 2016) on the neuron shown in Eq. (5), it is updated by
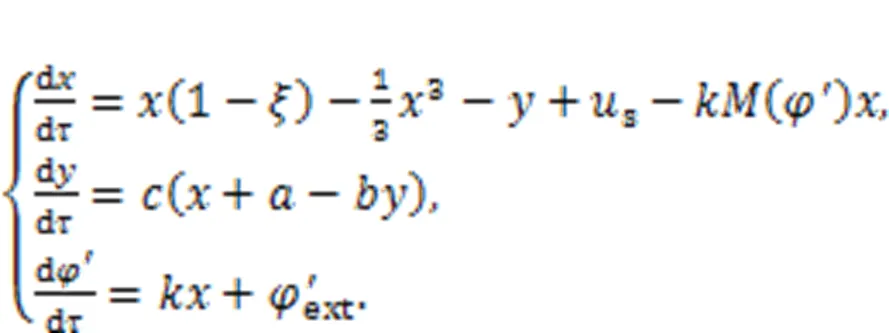
Physically, a memristor is connected to the RLC neural circuit in an additive branch circuit, activating a memristive channel via magnetic flux.′extdiscerns the effect of external electromagnetic radiation, which has a significant impact on the magnetic flux that covers the cell membrane. The normalized parameter=1/, which means that the inner magnetic field in the cell is approached by the field in the induction coil withturns. Therefore, field energy is kept as electric field energy and magnetic field energy in the inductor and memristor as well. For a magnetic flux-controlled memristor, the inner field energy is estimated by
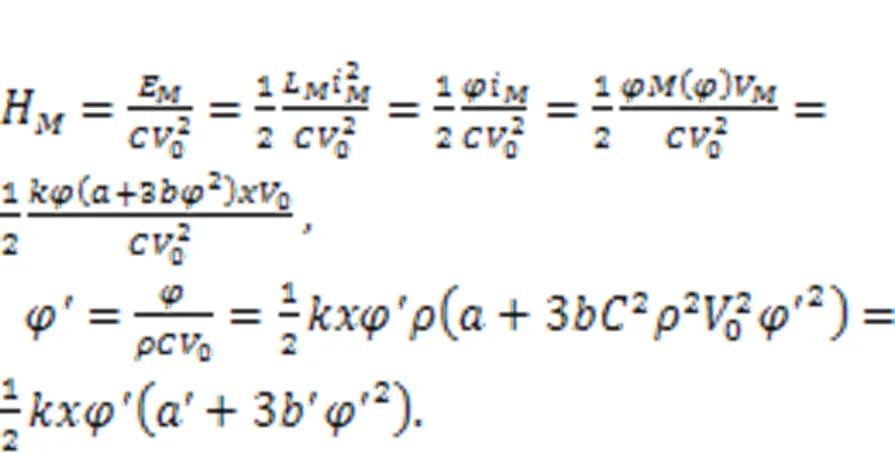
Therefore, the involvement of memristors in a neural circuit enables activation of a memristive channel/synapse, allowing field energy to be saved and exch anged among the three kinds of electronic components.
2.2 Memristive synapses connecting neurons
When a memristor is used to couple two neural circuits, the coupling channel becomes controllable by means of an external physical field, and the channel currenti=()(-′) across the memristor effectively regulates the synchronous behaviors of two neurons. The similar induction current()can be introduced into other neuron models to obtain more memristive neurons to explore control of neural activities in an isolated neuron and neural networks (Xu et al., 2018b; Etémé et al., 2019; Mondal et al., 2019; Mostaghimi et al., 2019). In particular, this scheme can be used to improve the cardiac tissue model, which enables assessment of the effect of electromagnetic radiation on wave propagation in the heart (Ma et al., 2017; Wu et al., 2017). For example, the initial state begins from a spiral wave, which is associated with arrhythmia; breakup occurs with increased intensity of EM, and ventricular fibrillation (VF) causes rapid death of the heart. When a target wave is initiated for behaving normal wave emitting from the sinoatrial node (SN), higher EM will block propagation and diffusion of the target wave; then regulation of the calcium current is terminated, resulting in suppression of the heartbeat that blocks blood from being pumped in the heart.
On the other hand, field coupling is activated between these biological neurons via exchange of magnetic flux. The collective behaviors of neural network under field coupling (Guo et al., 2017; Xu Y et al., 2018a, 2019; Lv et al., 2019; Zhou and Wei, 2021; Ramakrishnan et al., 2022) accompanied by synapse connections can be explored by
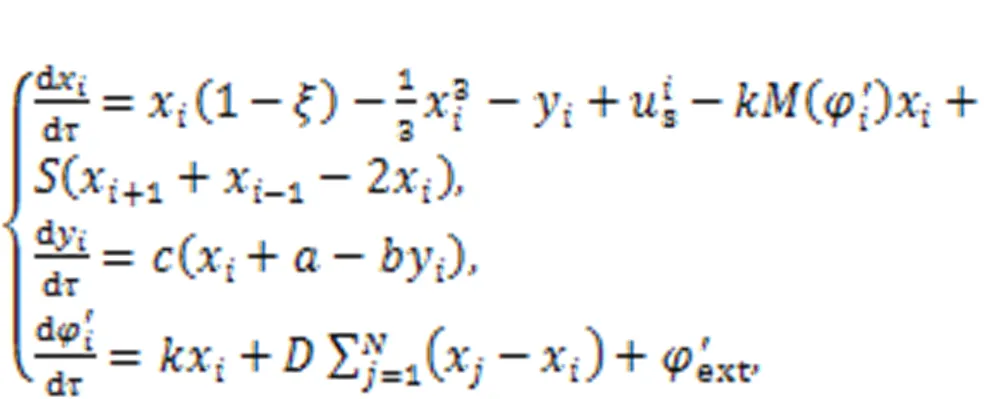
wheredenotes synaptic intensity. The array indicates an electric synapse at constantand how setting a specific function forcan represent functional synapses. The second term in the third formula in Eq. (8) means that superposition of a magnetic field on theth neuron in the network and the gaincan be dependent on the node position or considered as a constant for uniform field coupling. In the absence of synaptic coupling, these memristive neurons can be excited to exhibit resonance synchronization.
Above all, memristive terms are introduced to estimate the effect of the inner magnetic field of biological neurons, and the exchange of field energy between neurons is approached by using the exchange and accommodation of magnetic flux. In fact, when capacitors, inductors, and memristors are used to bridge connections to neural circuits, pure functional synapses and hybrid synapses (Yu et al., 2012, 2017; Liu et al., 2019a; Yao and Wang, 2021, 2022) are built for trigger-field coupling (Liu et al., 2019b, 2020; Ma SY et al., 2019; Xu YM et al., 2019; Yao et al., 2021b).
2.3 Thermosensitive neurons and temperature- dependent neural circuits
Thermistor resistance is dependent on temperature, and the current across a thermistor is controlled by external temperature when it is connected to a branch circuit of a nonlinear circuit. For a thermistor with negative temperature coefficient (NTC), the resistance is often estimated by
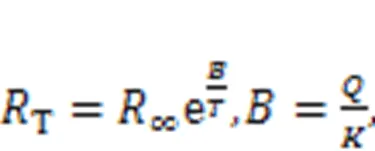
where∞r(nóng)epresents the resistance when the temperatureis extremely high (→∞); the parameteris associated with the material property;anddescribe the activation energy and Boltzmann's constant, respectively. When the linear resistor(Fig. 1) is replaced by a thermistorT, the channel current across the induction coil will also be controlled by temperature. On the other hand, replacingsin Fig. 1 means that external stimulus is controlled by temperature, and thus any changes will adjust the excitability of neuron and electric activity as well. In particular, when two thermistors are used to replace the two resistors in the model shown in Fig. 1, the neural circuit is controlled by temperature, and a thermosensitive neuron model is obtained as follows (Xu et al., 2020):
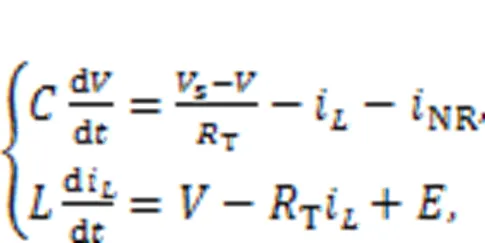
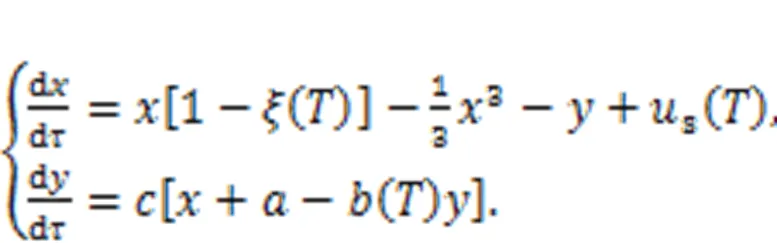
That is, more parameters and external stimuli are dependent on the temperature, and this neuron can be used to detect changes in temperature (Zhu et al., 2021). In the presence of noisy disturbance, stochastic resonance can be induced, and regularity in electric activity under appropriate noise intensity can be detected in the sampled time series for membrane potential. When more thermosensitive neurons are connected in a neural network, the spatial patterns can be controlled by the temperature and the distribution of Hamilton energy in the neural network shows distinct patterns (Xu and Ma, 2022).
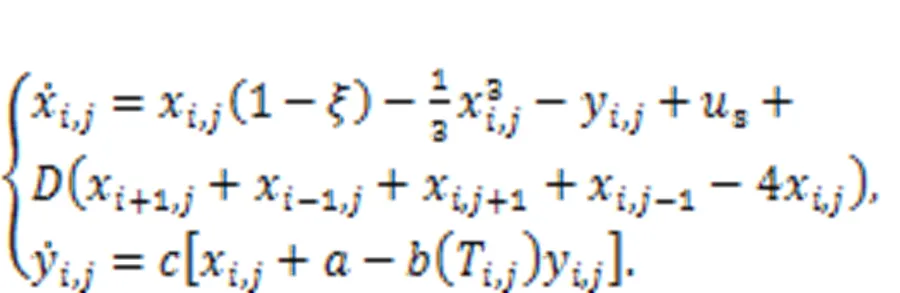
By changing the temperature-dependent parameters, the synchronization factor SF in the square array is estimated to predict the synchronization stability, as follows:
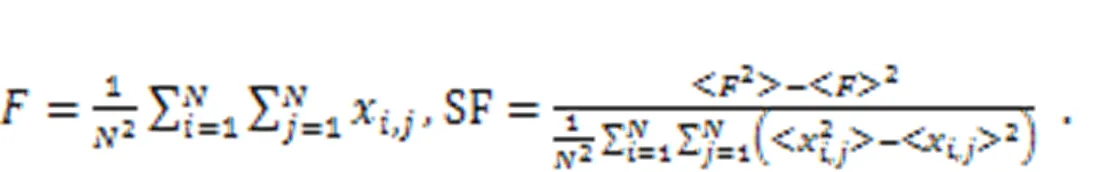
2.4 ?Auditory neurons and piezoelectric neural circuits
Piezoelectric ceramics can convert acoustic waves and mechanical force into electric signals, and they are often used as sensors and energy harvesters to collect energy from external noisy disturbance. As described by Zhou et al. (2021a), piezoelectric ceramics were used to capture an external voice, and a piezoelectric neural circuit was designed by replacing the signal sources(Fig. 1), while a piezoelectric neuron was proposed to simulate the response mechanism of auditory neurons. The external acoustic wave and vibration was perceived by the piezoelectric ceramics, and equivalent voltage was induced to excite the neural circuit.
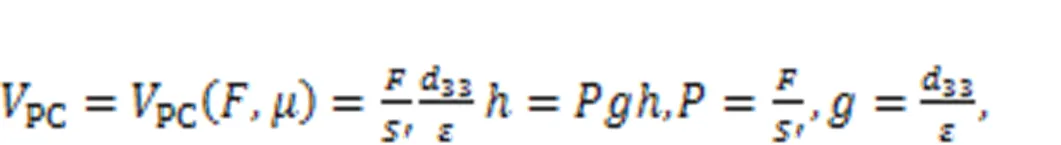
where ε is the dielectric constant; Sand h represent the cross-sectional area and thickness of the piezoelectric ceramics, respectively. As is well known, humans have a pair of ears, so they respond to external acoustic waves synchronously. In Fig. 2, one can see how the coherence response was investigated by driving two piezoelectric neural circuits without synaptic coupling.
The coupled auditory neurons predict the resonance synchronization based on the dynamical equations derived from the circuit equations for Fig. 2, as follows:
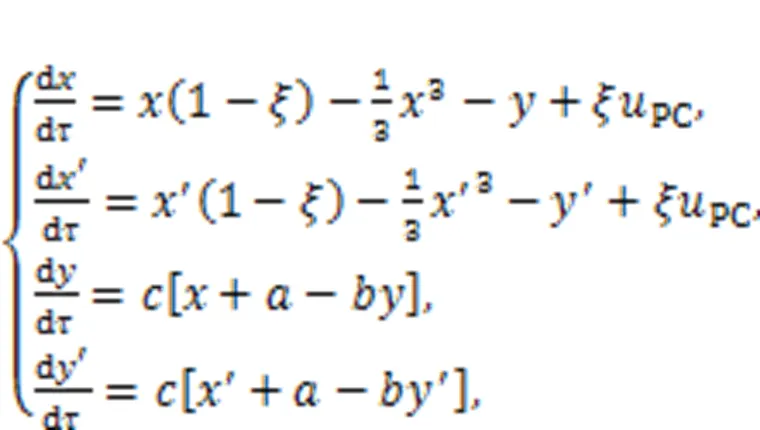
wherePCdefines the current generated from the piezoelectric ceramic.
The equivalent voltage generated from the piezoelectric ceramic part can be considered as a combination of periodic signal accompanied by Gaussian white noise.
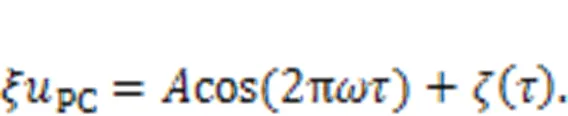
It was found that noisy disturbance was helpful to discern periodic signals exactly under stochastic resonance because of additive energy injection, and two auditory neurons reached perfect resonance synchronization even when synaptic coupling was removed completely. When more signal sources were activated, the auditory neuron received signals from more channels and signal detection became competitive. That is, when nervous systems are stimulated by more signals, fast and accurate selection of body gaits is dependent on the mode selection in an isolated neuron and cooperation between more functional neurons (Fourcaud-Trocmé et al., 2003; Guan and Rao, 2003; Mukamel et al., 2010; Turrigiano, 2012; Yu et al., 2021). As mentioned in recent studies, auditory neurons prefer to respond to external stimuli with higher energy and the final firing pattern is mainly controlled by the firing mode resulting from external forcing hold with higher energy (Xie and Ma, 2022; Xie et al., 2022c).
2.5 ?Visual neurons and light-sensitive neural circuits
Animal eyes can see objects by capturing reflected light; this causes a fast response in visual neurons which enables gait safety and promotes good decision-making. Light passes through the pupil and causes sensitization in the retina, and then electric signals are propagated to wake the neurons in the visual cortex for further signal processing. As reported by Liu Y et al. (2020) and Xie et al. (2021a), a phototube is incorporated in the RLC circuit of a model and external illumination is applied to activate the phototube to generate photocurrent. This model can be considered an artificial eye under photoelectric conversion. That is, the voltage sourcesis replaced by a photocell in Fig. 1. In fact, the form of photocurrent across the phototube is relative to the resistance of resistorsand will reach a saturation value when the frequency of external illumination is beyond a certain threshold.
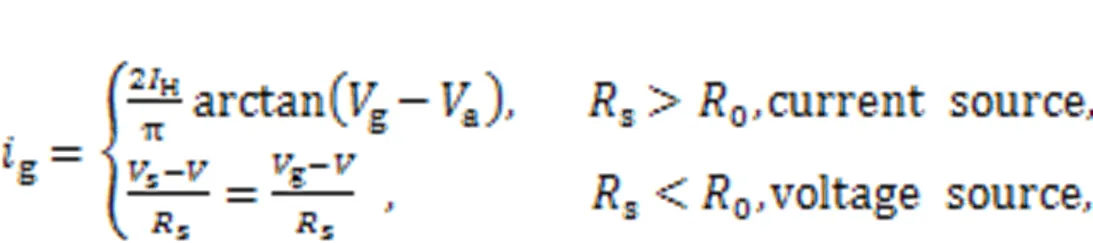
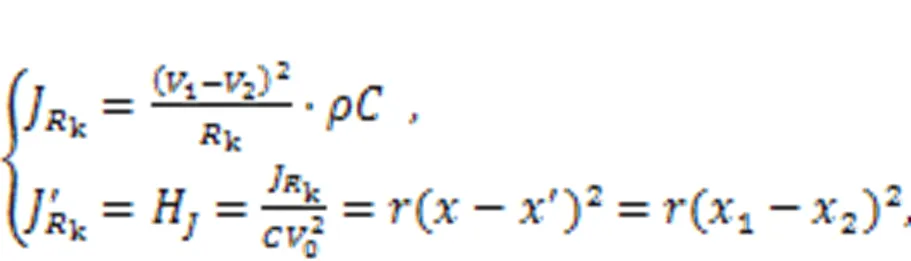
wherekdenotes the coupling resistor, andrepresents the coupling intensity for two neurons via electric synapse coupling. Because of its controllability, a phototube is used to couple two neural circuits, and external illumination is applied to adjust the coupling channel, while phase lock is controlled completely (Zhang XF et al., 2021a). In (Yao et al., 2021a), a hybrid synapse was designed to trigger field coupling between a light-sensitive neuron and a thermosensitive neuron, and the results reveal the cooperation between neurons from different functional regions.
2.6 Josephson junction coupled neuron under a magnetic field
A Josephson junction is a specific electric component with particular inductance properties (Crotty et al., 2010). Zhang Y et al. (2021) used an ideal Josephson junction to replace the external voltage sourcesas shown in Fig. 1, and described the circuit equations:
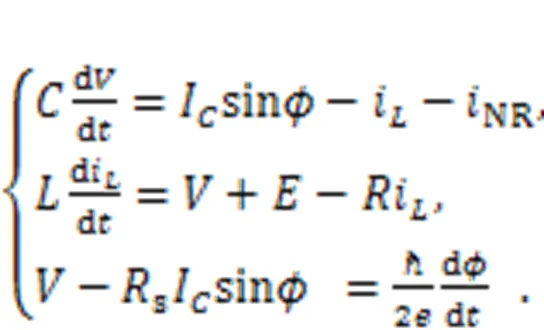
The parameter=/(2π),is the Planck constant, andis the electron charge. The variablecalculates the phase error for the Josephson junction. Similar scale transformation is applied for the physical variables and parameters in Eq. (18), as follows:
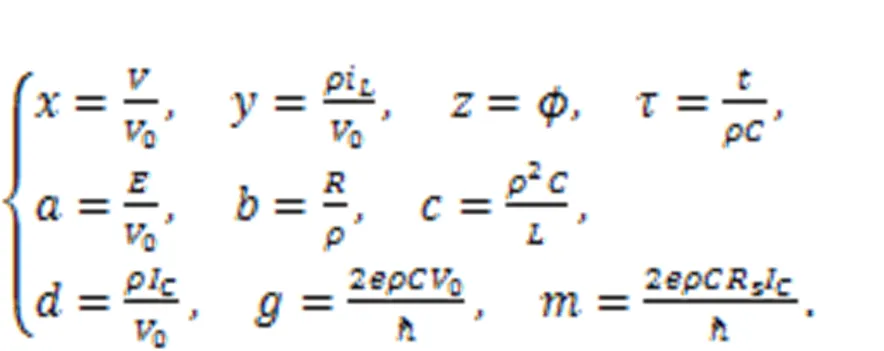
In addition, the dynamics of a neural circuit coupled with a Josephson junction were calculated by Zhang Y et al. (2021):

In the presence of an external magnetic field, the phase error for the junction and channel current are updated by
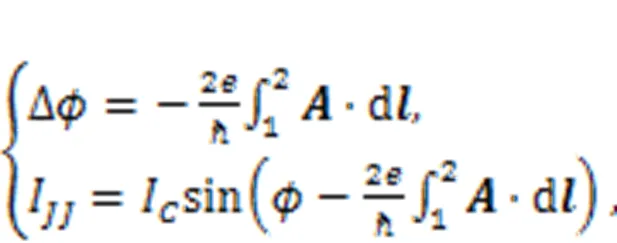
whereis the magnetic vector potential for the external magnetic field, and 1, 2 indicate the two end sides of the junction. That is, the external magnetic field generates additive phase error in the junction and then the channel current is regulated by the external field. As a result, the fluctuation of the magnetic field will induce changes in the channel current, which controls the firing modes of the neuron; in this way, the neural circuit can be used to detect the magnetic field. Furthermore, both a memristor and a Josephson junction are incorporated into the RLC circuit to discern the effect of magnetic field and inner electromagnetic induction (Zhang Y et al., 2020a). Zhang et al. (2018a, 2018b) estimated the distribution in each electronic component and detected similar stochastic resonance when there was noise. The involvement of a Josephson junction allows accurate description of the effect of a magnetic field on ion channels. Readers can refer to more studies on the application of Josephson junctions in neural circuits and synchronization stability of neurons under magnetic field (Segall et al., 2017; Zhang et al., 2018a, 2018b; Foka et al., 2021; Goteti and Dynes, 2021; Mishra et al., 2021; Chalkiadakis and Hizanidis, 2022; Fossi et al., 2022).
3 Selection and filtering in frequency
The realistic nervous system can perceive external physical stimuli within specific bands. In the presence of noise and electromagnetic radiation, external energy is injected partially and appropriate firing modes can be triggered. As reported in our previous work, auditory neurons developed from piezoelectric neural circuits are preferable because they respond to external forces with higher energy (Xie and Ma, 2022; Xie et al., 2022c). As a result, multiple inputs and exciting from more channels induce competition in the response mode in the neuron, and the final firing patterns are mainly controlled by the firing mode associated with higher energy. Animal eyes are sensitive to visible lights with wave lengths between 390 nm and 780 nm and frequency bands of 380–?750 THz. Humans can perceive acoustic waves within the frequency band 20–20000 Hz, while bat can discern the ultrasonic beyond 20?000 Hz. Physically speaking, wave filtering in biological neurons and functional electric components achieves restriction of amplitude and frequency as well.
3.1 ?Phase-space compression and amplitude restriction
For dynamical systems, the variables develop their orbits in the phase space and the orbits become dense in the presence of chaos. When some of the orbits are restricted and re-guided, chaotic states will be suppressed because dense orbits are reduced and combined to develop periodic orbits or stable equilibrium points. Luo (1999) suggested a scheme to control chaos and hyperchaos by using phase-space compression, by which the output variables are constrained within a range. In addition,Ma et al. (2008) explained the dynamical mechanism as amplitude restriction and physical realization for the scheme of phase-space compression via the Heaviside function. For a low-dimensional chaotic system, the dynamics are represented by
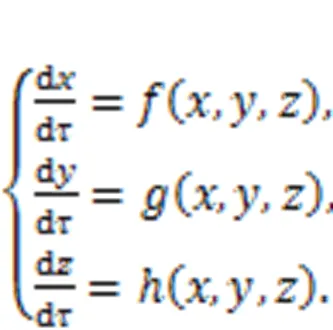
The output variables (,,) are restricted as follows by setting different thresholds (max,max,max,min,min,min).
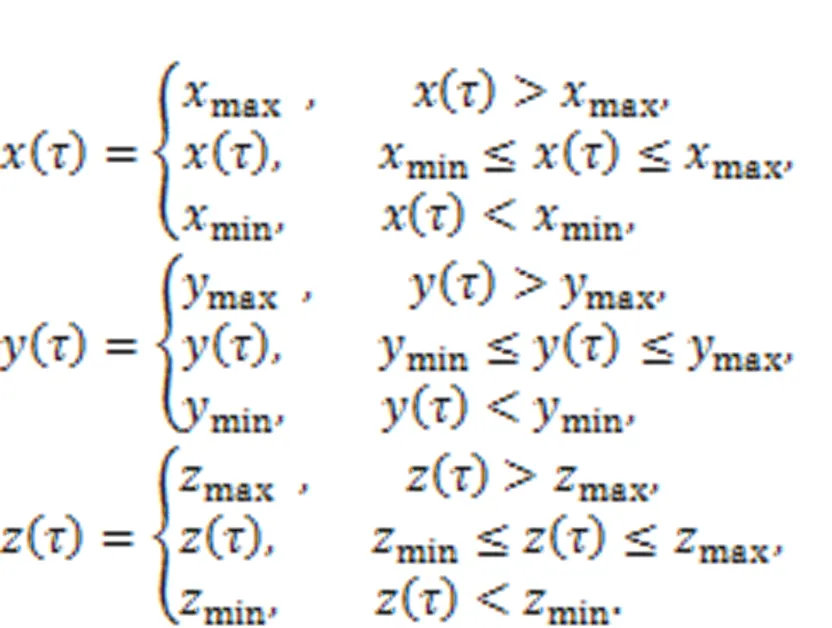
In experiment and dynamical control, the control criteria in Eq. (23) mean appropriate controllers are applied on the right side of the chaotic system Eq. (22), and these controllers can be achieved by using the Heaviside function as follows:
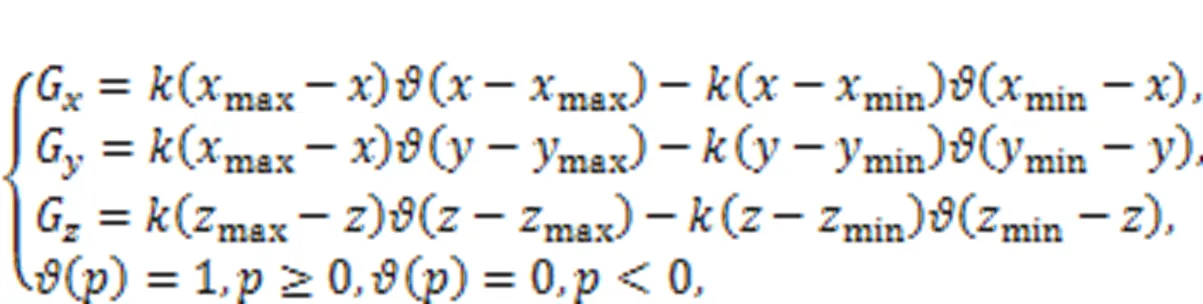
whereis the feedback gain. By setting the same thresholds in Eq. (24) as for Eq. (23), the gaincan be adjusted to reach the same target orbits. The implementation of controllers in Eq. (24) explains the dynamical and physical mechanism for the scheme of phase-space compression, and it is seen to be a kind of amplitude control scheme. The scheme is also effective for controlling collective behaviors in networks composed of chaotic oscillators (Zhang and Shen, 2001; He et al., 2003; Zamen and Dehghan-Niri, 2019). For example, target waves can be developed when a few nodes are controlled by phase-space compression by inducing continuous wave fronts (Gao et al., 2008). This scheme is also effective for controlling spiral waves and spatiotemporal chaos in neural networks (Ma et al., 2009; Li Y et al., 2017).
3.2 ?Wave filtering and frequency selection in neurons
Realistic acoustic waves and visible lights often present finite wavelengths and frequency bands. Photoelectric conversion and piezoelectric conversion depend on the material properties of the photocell and piezoelectric device, and only finite frequency bands can be perceived and converted into effective electric signals. External electromagnetic waves and acoustic waves are filtered by the electronic components and organs of animals, and the sampled time series for realistic signals are represented as(); these can be derived from chaotic systems or experimental data.
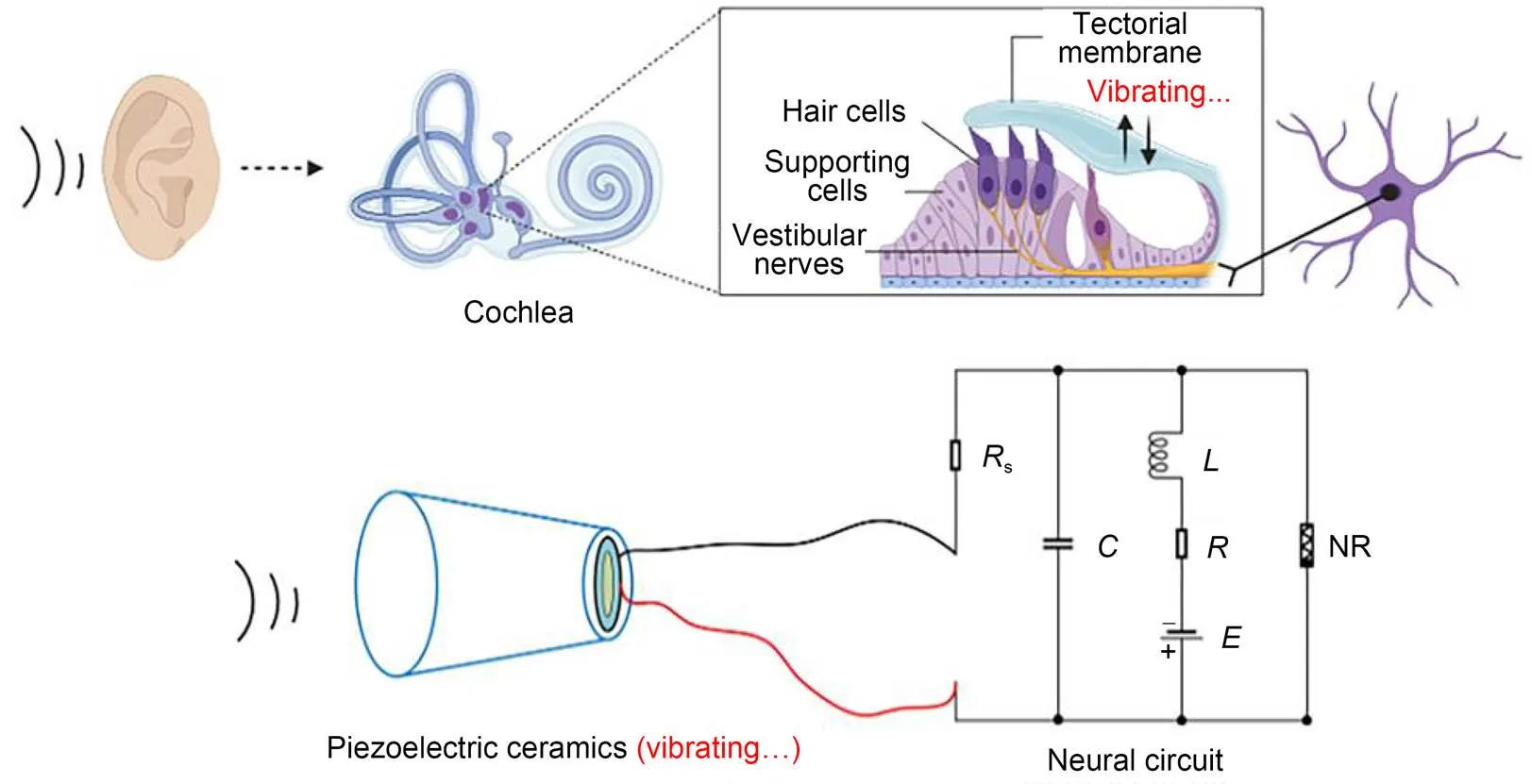
Fig. 3 Schematic diagram for a piezoelectric neural circuit and workflow in the auditory system
As suggested by Guo et al. (2021) and Zhang and Ma (2021), a criterion for frequency selection can be defined to control the photocurrent and piezoelectric current in order to regulate the visual neuron and auditory neuron, respectively.
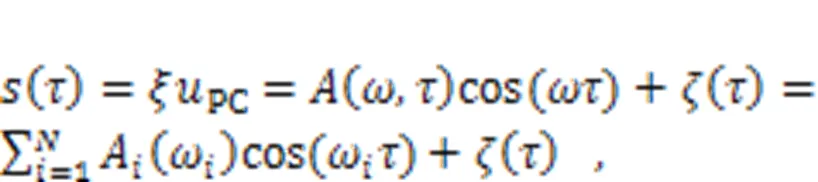
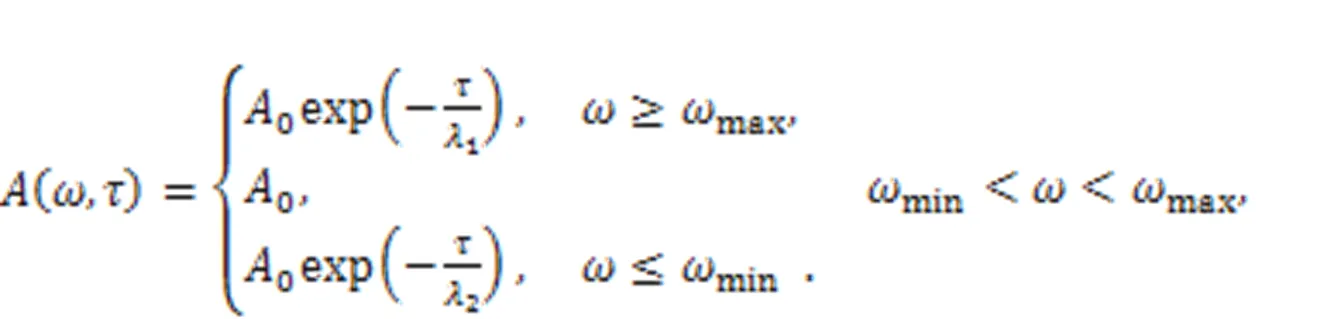
The realistic signal is often accompanied with certain noise. The electric components for the energy harvester and signal conversion just pass physical signals within a specific frequency band, and the other frequency bands are absorbed completely. The gains (1,2) are associated with the intrinsic material properties of the electric components. Frequency selection can be realized experimentally via combined Heaviside functions, and noise is also filtered as follows:
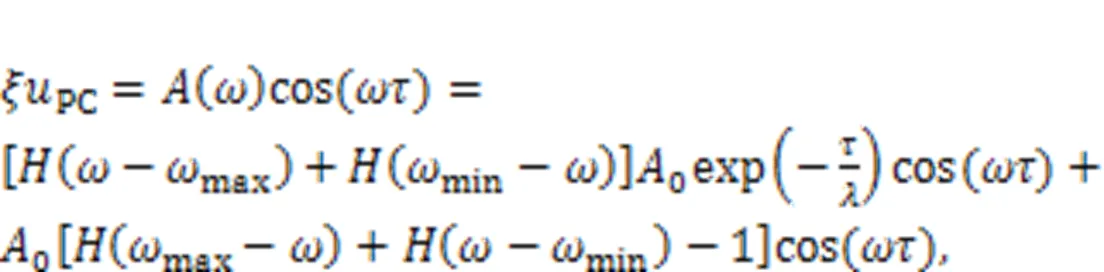
or another expression as follows:
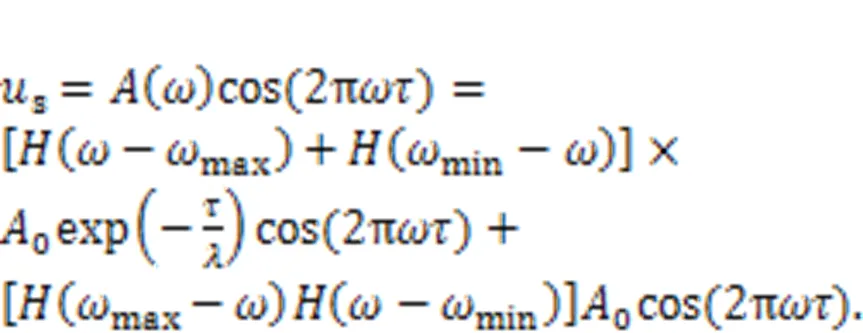
This scheme is much different from the phase-space compression scheme focused on amplitude control. After wave filtering and frequency selection, the external stimuli regarded as mixed signals()=1cos1+2cos2+…+acosω+…+acosωare filtered to keep a combination of signals with specific frequencies rather than a distinct periodic signal. Chaotic series from the known chaotic systems can be used practically as realistic signals with wide frequency, and these chaotic signals are described by an equivalent frequency spectrum in the frequency domain space. The functional components can be coated with different films including piezoelectric ceramic and photocell films, and then the thresholds for wave filtering can be controlled effectively. The coated film absorbs the physical stimuli when their intrinsic frequency is beyond or below the suggested threshold. As a result, wave filtering is accomplished and external stimuli within a specific frequency band can be precisely discerned. For a pair of eyes and ears, two piezoelectric neurons and two light-sensitive neurons developed from neural circuits driven by photocurrents can be used to investigate with a resonance synchronization approach, without synaptic coupling between neurons. For more extensive application, the two functional biophysical neurons can be connected in a chain network or networks on a square array with a long-range connection, and gradient stimuli can be applied to study the formation and regulation of wave propagation from heterogeneity and defects in the neural network.
In the phototube and piezoelectric ceramics, a coating film can control the thresholds for wave filtering. For auditory and visual neurons, similar frequency selection can be realized due to specific biophysical functions in the retina and eardrum. In most previous research, distinct periodic stimuli have been imposed on finite neurons/nodes in local areas of the network, and this pinning control induces continuous wave fronts and development of regular patterns. Inspired by the previously mentioned scheme of wave filtering, mixed signals with finite frequency bands can be used to control the collective behaviors of neural networks, and wave propagation and pattern formation can thus be regulated in practice.
4 Hamilton energy and synapse growth
Static intracellular ions including calcium, sodium, potassium, and chloride can develop static electric fields, and continuous pumping and diffusion of these intracellular ions can induce time-varying magnetic fields. In presence of external stimulus or stimuli accompanied with noise and EM, channel currents are changed to adjust membrane potential and the distribution of the inner electromagnetic field is changed. These biological neurons are charged bodies with non-uniform distribution of the electromagnetic field, and energy exchange occurs when more neurons are clustered (gathered) closely in the same region because of superposition in the electromagnetic field. Biological neurons and cells are often flexible, and their synapses are forced to bridge connections to adjacent neurons for fast balancing of ion concentration, membrane potential, and energy. Most previous work has emphasized the functions of electric synapses, chemical synapses, and even hybrid synapses in informing encoding, as well as synchronous regulation in neurons and neural networks (Sun and Si, 2020; Paul Asir et al., 2021; Si and Sun, 2021; Xu et al., 2021; Peng et al., 2022; Zhou et al., 2022b). Synaptic coupling is also effective in controlling synchronous electric activity because of synaptic plasticity (Yang et al., 2017; Lu et al., 2019; Taher et al., 2022; Tuo and Yang, 2022). Dynamically, synaptic plasticity enables self-adaption of biological neurons and feasible adjustment of coupling channels. It is interesting to explain the controllability mechanism of synapses connecting to biological neurons. First, the author of this review clarified that the creation and growth of synapses result from the energy diversity between neurons, and the intensity of synaptic coupling is controlled to reach a saturation value, while energy balance is maintained between neurons (Xie et al., 2022b; Zhou et al., 2022a). Furthermore, the adaptive growth criterion is used to investigate the activation and growth of hybrid synapses, while field coupling is controlled to regulate phase lock and synchronous firings in neurons (Ma and Xu, 2022; Wang and Ma, 2022; Wang CN et al., 2022; Wang Y et al., 2022; Xie et al., 2023). The energy in biological neurons and neuron models is different from the metabolic energy in the nervous system (Bélanger et al., 2011; Jha and Morrison, 2018; Yuan et al., 2018; Bonvento and Bola?os, 2021; Pal et al., 2021), and the energy function is composed of membrane potential and recovery variables for currents (Pinto et al., 2000; Torrealdea et al., 2006, 2009; Moujahid et al., 2011). Sarasola et al. (2004) defined generic Hamilton energy function for chaotic systems and approached it using the Helmholtz theorem (Kobe, 1986; Heras, 2016). The generic dynamical system is expressed with equivalent vector form, as follows:
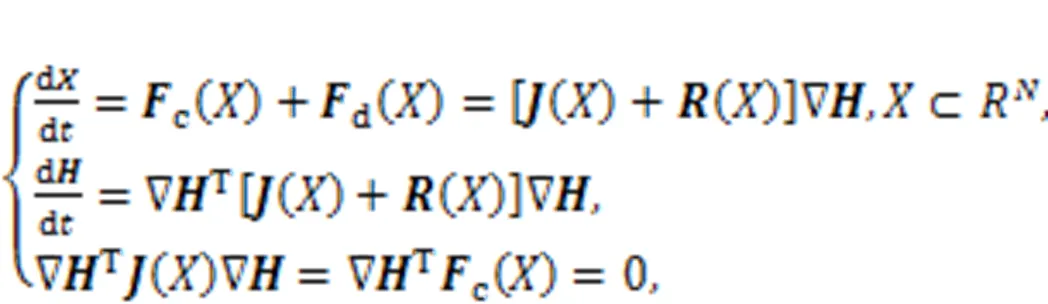
where() and() define the skew symmetric matrix and principal diagonal matrix, respectively.c() andd() represent the transverse vortex field and gradient field, respectively, anddenotes the Hamilton energy for this dynamical system. Zhou et al. (2021b) also clarified that the most suitable Lyapunov function should be the Hamilton energy function, which can be mapped from the field energy function for equivalent nonlinear circuits. For the simple neuron in Eq. (5), it can be updated by
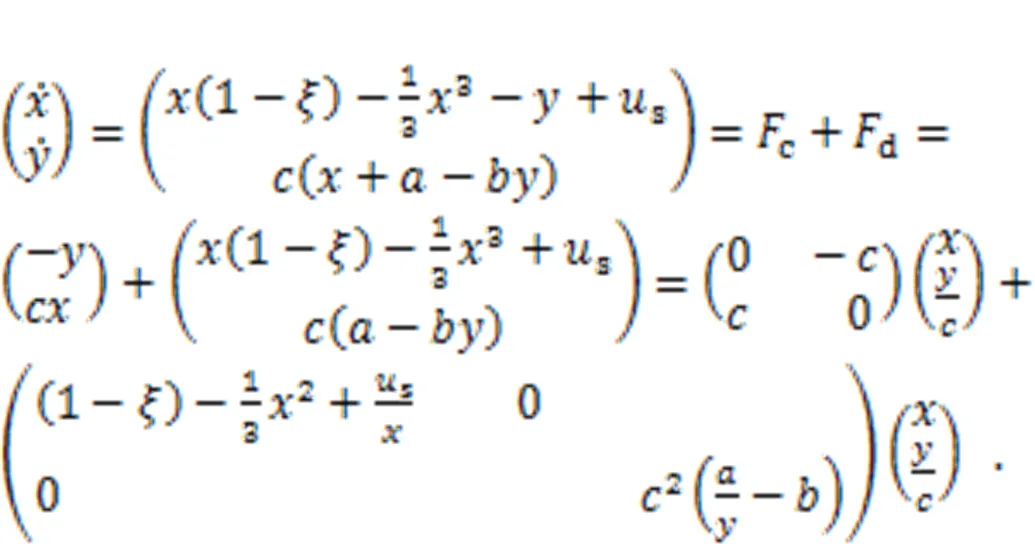
The Hamilton energyfor the two-variable neuron model can be derived from
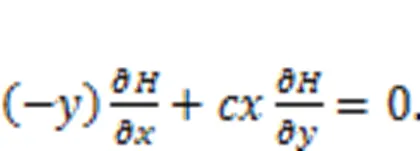
Surely, the sole Hamilton energy function in Eq. (5),=0.52+0.52/, meets the criterion in Eq. (28). For two neurons, the energy diversity is defined as follows:
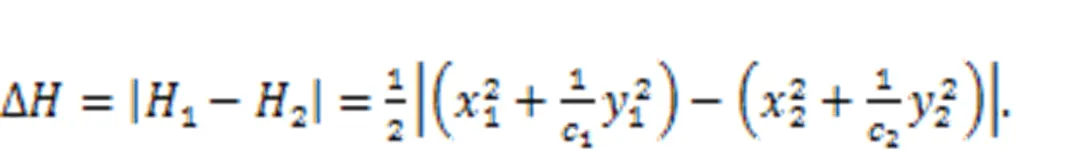
For neural networks, the energy diversity for each neuron is mainly dependent on the adjacent neurons.
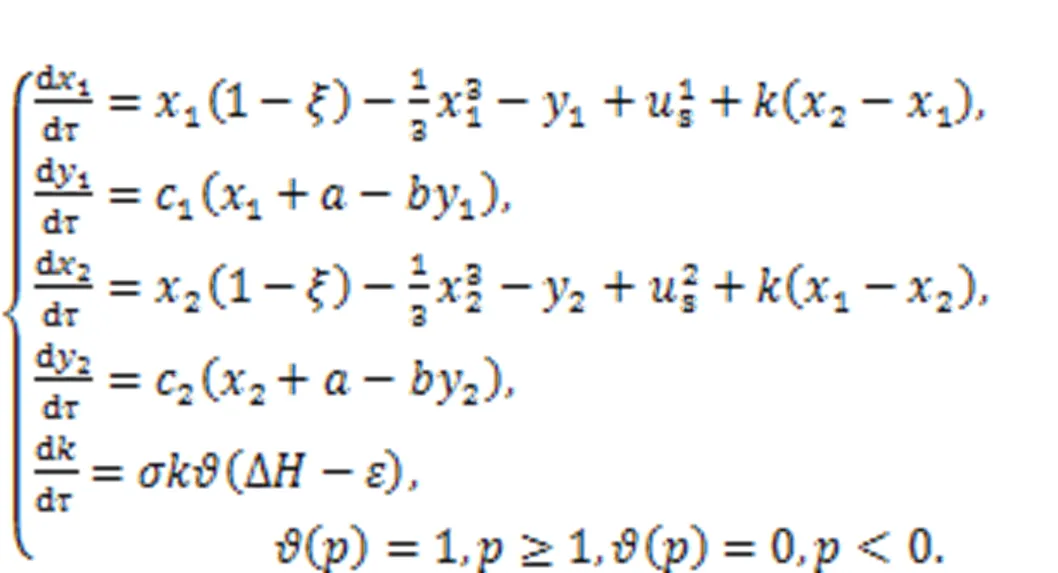
The coupling intensitycan be selected with an appropriate function to describe the electric synapse, chemical synapse, memristive synapse, and even hybrid synapse. Synapse growth is controlled by the Heaviside function when energy diversity between neurons is beyond the threshold(about 0.00001). When two neurons reach energy balance and the energy diversity is decreased to be close to, the coupling intensity and gain terminate its further increase and a saturation value is reached, accompanied by complete synchronization between two identical neurons, as well as phase lock among non-identical neurons. Furthermore, additive noise and multiplicative noise can be imposed to discuss the synchronization approach between neurons, and this growth criterion for synaptic coupling provides new insights for understanding the growth and creation of synapses in biological neurons.
5 ?Heterogeneity and defects in neural networks
Neural activities in the nervous system can be explored in neural networks by investigating the wave propagation and pattern formation in one-layer or multi-layer networks. In a uniform network, the local kinetics is described by neurons with the same parameter settings, and coupling channels are often endowed with the same biophysical properties. In realistic biological networks and neural networks, each node has some difference in the biophysical properties and link densities; as a result, heterogeneity and defects develop (Xie et al., 2022a). In a generic network, the dynamics are described by
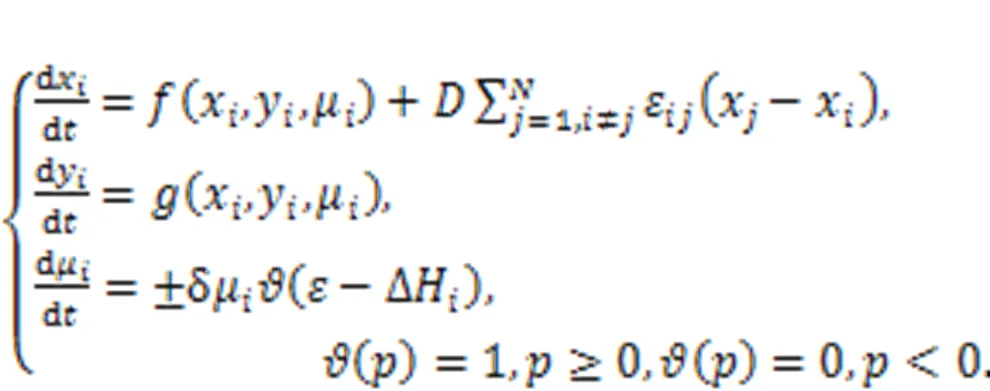
For simplicity, the local kinetics of the network can be described by the above-described two-variable neuron. The coupling intensityis controlled by the energy diversity among adjacent neurons. Xie et al. (2022d) claimed that fast energy accommodation or external energy injection into a local area would induce shape deformation, causing some intrinsic parameters to show particular shapes. When the local area collects and maintains a higher energy value, heterogeneity is formed, and wave fronts can be emitted to regulate the collective behaviors of the network. On the other hand, defects are formed when a local area continues to release energy and has a lower energy value, and wave propagation will be blocked in the network. In fact, heterogeneity and defects can be developed in the excitable media and oscillatory media, and this phenomenon can also be described by networks and reaction-diffusion equations (Chen and Chandra, 2004; Chen et al., 2009; Benmarhnia et al., 2018; Rostami and Jafari, 2018; Huang et al., 2020; Rajagopal et al., 2021). Readers can explore the formation of heterogeneity in networks controlled by energy flow according to the suggestions in (Xie et al., 2022d).
Above all, the studies summarized here provide scientific evidence that clarifies the biophysical function of new neuron models. Neuron models which are claimed to be reliable should discern the physical effect clearly. Many neuron models described by continuous differential equations are improved by supplying additive magnetic variables and induction current terms, and memristive neuron models are thus obtained. However, it is a challenge to estimate the effect of electromagnetic induction on discrete neuron models. Based on the Rulkov neuron model (Rulkov, 2001), a discrete memristor can be introduced to estimate the field effect by adding induction current in a discrete form. The current across the discrete memristor is defined by
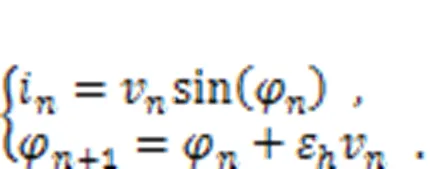
The second formula in Eq. (34) is regarded as a discrete form for Faraday's law of electromagnetic induction, and the intrinsic parameterεcan be viewed as a time scale factor dependent on the physical properties of the memristor. The memductance of the discrete memristor is described by sin(φ) or another form, tanh(φ), andvrepresents the voltage across the memristor. When the memristor is connected to the Rulkov neuron and additive channel current is shunted, the effect of electromagnetic induction can be determined as follows (Li et al., 2022):
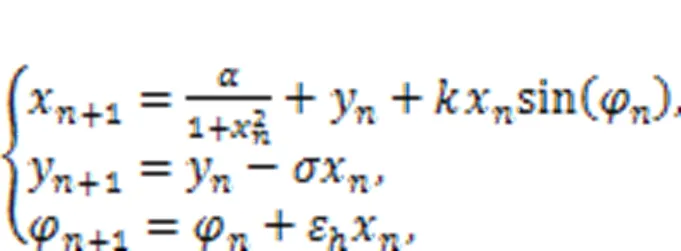
where the gainis relative to the property of the neural circuit, and the normalized parameters (,ε,) and initial value for magnetic fluxcan be adjusted to change the excitability of the neuron; then the bursting patterns can be controlled effectively. The same scheme can be applied for other discrete chaotic maps, and the chaos can be controlled effectively (Bao BC et al., 2020; Peng et al., 2020; Bao H et al., 2021; Deng and Li, 2021). Based on these memristive neuron models, external electromagnetic radiation is often estimated by imposing noisy disturbance on the magnetic flux. In particular, Li JJ et al. (2016) suggested another algorithm to estimate electromagnetic radiation by converting absorption power into equivalent transmembrane current on the temperature-dependent neuron. Besides, enhancement of biophysical function of neuron models, interaction with astrocytes (Li J et al., 2016; Li JJ et al., 2017; Du et al., 2018; Yu et al., 2022), and clarification of their role provide helpful clues to possibilities for curing seizures. More importantly, as suggested by Wang R et al. (2019), a clear brain functional network is useful for combining these biophysical neurons to build a realistic neural network for discerning cooperation between different functional regions in the brain.
We believe that the most valuable aspect of this review is the clarification of proposals for some functional biophysical neuron models from the physical angle. In particular, the functional role of intrinsic energy in neurons is explained. It guides energy flow to control the firing modes and growth of neural synapses. When energy flow is shunted and pumped, self-adaption of biophysical neurons is activated and released. Energy flow accounts for the biophysical regulation of neural activities in the brain and nervous system. For extensive guidance and help, readers can be inspired by the following important reviews (Trench ard and Perc, 2016; Parastesh et al., 2021; Gosak et al., 2022; Majhi et al., 2022). The references therein, as well as the collective behaviors described (including coexistence of synchronization and desynchronization, chimeras, and higher-order interaction in neural networks) are worthy of further exploration.
6 Conclusions
In this review, we describe how a group of biophysical neuron models has been developed from neural circuits by incorporating different specific electronic components including memristors, thermistors, phototubes, piezoelectric ceramics, and Josephson junctions. Synapse function is enhanced by designing hybrid synapses with the physical aspects in mind. The inner field energy of neurons can be described by equivalent Hamilton energy, which decides the firing modes and patterns. The creation and growth of synapses to connect biological neurons are explained from a physical viewpoint, which allows us to confirm that energy diversity controls synaptic regulation to maintain a stable energy balance. In particular, the formation of heterogeneity results from energy accommodation, and shape deformation is generated, accompanied by a parameter shift in the theoretical model. Some new insights within this review will be helpful for further investigation in nonlinear dynamics, computational neuroscience, and application of artificial neural circuits.
This project is partially supported by the National Natural Science Foundation of China (No. 12072139). This review summarized some recent studies contributed by Drs. Mi LV, Ying XU, Fu-qiang WU, Zhi-long LIU, Zhao YAO, Ying ZHANG, and Ying XIE (Chongqing University of Posts and Telecommunications, China), and Prof. Ping ZHOU (Lanzhou University of Technology, China).
All data generated or analyzed during this study are included in this review.
Jun MA declares no conflict of interest with this publication.
AbdelAty AM, Fouda ME, Eltawil AM, 2022. On numerical approximations of fractional-order spiking neuron models., 105:106078. https://doi.org/10.1016/j.cnsns.2021.106078
Abidi AA, Chua LO, 1979. On the dynamics of Josephson-junction circuits., 3(4):186-200. https://doi.org/10.1049/ij-ecs.1979.0031
Ahmad I, Wang X, Zhu MX, et al., 2022. EEG-based epileptic seizure detection via machine/deep learning approaches: a systematic review., 2022:6486570. https://doi.org/10.1155/2022/6486570
Bailoul CE, Alaa NE, 2020. Modelling and simulation of transmission lines in a biological neuron., 13(2):224-234. https://doi.org/10.1504/IJCBDD.2020.107320
Bao BC, Li HZ, Wu HG, et al., 2020. Hyperchaos in a second-order discrete memristor-based map model., 56(15):769-770. https://doi.org/10.1049/el.2020.1172
Bao H, Hua ZY, Li HZ, et al., 2021. Discrete memristor hyperchaotic maps., 68(11):4534-4544. https://doi.org/10.1109/TCSI.2021.3082895
Bashkirtseva I, Nasyrova V, Ryashko L, 2018. Analysis of noise effects in a map-based neuron model with Canard-type quasiperiodic oscillations., 63:261-270. https://doi.org/10.1016/j.cnsns.2018.03.015
Baysal V, Yilmaz E, 2020. Effects of electromagnetic induction on vibrational resonance in single neurons and neuronal networks., 537:122733. https://doi.org/10.1016/j.physa.2019.122733
Baysal V, Erkan E, Yilmaz E, 2021. Impacts of autapse on chaotic resonance in single neurons and small-world neuronal networks., 379(2198):20200237. https://doi.org/10.1098/rsta.2020.0237
Bélanger M, Allaman I, Magistretti PJ, 2011. Brain energy metabolism: focus on astrocyte-neuron metabolic cooperation., 14(6):724-738. https://doi.org/10.1016/j.cmet.2011.08.016
Benmarhnia T, Alexander S, Price K, et al., 2018. The heterogeneity of vulnerability in public health: a heat wave action plan as a case study., 28(5):?619-625. https://doi.org/10.1080/09581596.2017.1322176
Bonvento G, Bola?os JP, 2021. Astrocyte-neuron metabolic cooperation shapes brain activity., 33(8):1546-1564. https://doi.org/10.1016/j.cmet.2021.07.006
Brekke E, Morken TS, Sonnewald U, 2015. Glucose metabolism and astrocyte?–?neuron interactions in the neonatal brain., 82:33-41. https://doi.org/10.1016/j.neuint.2015.02.002
Calabrese RL, Norris BJ, Wenning A, 2016. The neural control of heartbeat in invertebrates., 41:68-77. https://doi.org/10.1016/j.conb.2016.08.004
Chalkiadakis D, Hizanidis J, 2022. Dynamical properties of neuromorphic Josephson junctions., 106(4):044206. https://doi.org/10.1103/PhysRevE.106.044206
Chen JX, Xu JR, Zhang XP, et al., 2009. Controlling chaos by developing spiral wave from heterogeneity in excitable medium., 7(1):?108-113. https://doi.org/10.2478/s11534-008-0139-5
Chen SL, Zou Y, Zhang XD, 2019. An efficient method for Hopf bifurcation control in fractional-order neuron model., 7:77490-77498. https://doi.org/10.1109/ACCESS.2019.2920007
Chen X, Chandra N, 2004. The effect of heterogeneity on plane wave propagation through layered composites., 64(10-11):1477-1493. https://doi.org/10.1016/j.compscitech.2003.10.024
Corinto F, Forti M, 2016. Memristor circuits: flux-charge analysis method., 63(11):1997-2009. https://doi.org/10.1109/TCSI.2016.2590948
Crotty P, Schult D, Segall K, 2010. Josephson junction simulation of neurons., 82(1):011914. https://doi.org/10.1103/PhysRevE.82.011914
Davison EN, Schlesinger KJ, Bassett DS, et al., 2015. Brain network adaptability across task states., 11(1):e1004029. https://doi.org/10.1371/journal.pcbi.1004029
Deng Y, Li YX, 2021. Bifurcation and bursting oscillations in 2D non-autonomous discrete memristor-based hyperchaotic map., 150:111064. https://doi.org/10.1016/J.CHAOS.2021.111064
Du MM, Li JJ, Chen L, et al., 2018. Astrocytic Kir4.1 channels and gap junctions account for spontaneous epileptic seizure., 14(3):e1005877. https://doi.org/10.1371/journal.pcbi.1005877
Durkee CA, Araque A, 2019. Diversity and specificity of astrocyte–neuron communication., 396:73-78. https://doi.org/10.1016/j.neuroscience.2018.11.010
Elbasiouny SM, 2014. Development of modified cable models to simulate accurate neuronal active behaviors., 117(11):1243-1261. https://doi.org/10.1152/japplphysiol.00496.2014
Etémé AS, Tabi CB, Mohamadou A, 2019. Firing and synchronization modes in neural network under magnetic stimulation., 72:432-440. https://doi.org/10.1016/j.cnsns.2019.01.004
Flynn AM, Sanders SR, 2002. Fundamental limits on energy transfer and circuit considerations for piezoelectric transformers., 17(1):8-14. https://doi.org/10.1109/63.988662
Foka NFF, Ramakrishnan B, Tchamda AR, et al., 2021. Dynamical analysis of Josephson junction neuron model driven by a thermal signal and its digital implementation based on microcontroller., 94(12):234. https://doi.org/10.1140/epjb/s10051-021-00256-y
Fossi JT, Deli V, Edima HC, et al., 2022. Phase synchronization between two thermo-photoelectric neurons coupled through a Josephson junction., 95(4):66. https://doi.org/10.1140/epjb/s10051-022-00324-x
Fourcaud-Trocmé N, Hansel D, van Vreeswijk C, et al., 2003. How spike generation mechanisms determine the neuronal response to fluctuating inputs., 23(37):11628-11640. https://doi.org/10.1523/JNEUROSCI.23-37-11628.2003
Fraschini M, Demuru M, Crobe A, et al., 2016. The effect of epoch length on estimated EEG functional connectivity and brain network organisation., 13(3):036015. https://doi.org/10.1088/1741-2560/13/3/036015
Gao JH, Zheng ZG, Ma J, 2008. Controlling turbulence via target waves generated by local phase space compression., 22(22):3855-3863. https://doi.org/10.1142/S0217979208048644
Ge MY, Jia Y, Xu Y, et al., 2019. Wave propagation and synchronization induced by chemical autapse in chain Hindmarsh?–?Rose neural network., 352:136-145. https://doi.org/10.1016/j.amc.2019.01.059
Ge MY, Wang GW, Jia Y, 2021. Influence of the Gaussian colored noise and electromagnetic radiation on the propagation of subthreshold signals in feedforward neural networks., 64(4):?847-857. https://doi.org/10.1007/s11431-020-1696-8
Geethanath S, Vaughan JT, 2019. Accessible magnetic resonance imaging: a review., 49(7):e65-e77. https://doi.org/10.1002/jmri.26638
Giuriato G, Ives SJ, Tarperi C, et al., 2020. Timed synchronization of muscle contraction to heartbeat enhances muscle hyperemia., 128(4):?805-812. https://doi.org/10.1152/japplphysiol.00898.2019
Gosak M, Milojevi? M, Duh M, et al., 2022. Networks behind the morphology and structural design of living systems., 41:1-21. https://doi.org/10.1016/j.plrev.2022.03.001
Goteti US, Dynes RC, 2021. Superconducting neural networks with disordered Josephson junction array synaptic networks and leaky integrate-and-fire loop neurons., 129(7):073901. https://doi.org/10.1063/5.0027997
Graas EL, Brown EA, Lee RH, 2004. An FPGA-based approach to high-speed simulation of conductance-based neuron models., 2(4):417-435. https://doi.org/10.1385/NI:2:4:417
Grassia F, Buhry L, Lévi T, et al., 2011. Tunable neuromimetic integrated system for emulating cortical neuron models., 5:134. https://doi.org/10.3389/fnins.2011.00134
Guan KL, Rao Y, 2003. Signalling mechanisms mediating neuronal responses to guidance cues., 4(12):941-956. https://doi.org/10.1038/nrn1254
Guo SL, Wang CN, Ma J, et al., 2016. Transmission of blocked electric pulses in a cable neuron model by using an electric field., 216:627-637. https://doi.org/10.1016/j.neucom.2016.08.023
Guo SL, Xu Y, Wang CN, et al., 2017. Collective response, synapse coupling and field coupling in neuronal network., 105:120-127. https://doi.org/10.1016/j.chaos.2017.10.019
Guo YT, Zhou P, Yao Z, et al., 2021. Biophysical mechanism of signal encoding in an auditory neuron., 105(4):3603-3614. https://doi.org/10.1007/s11071-021-06770-z
Guo YY, Wang CN, Yao Z, et al., 2022. Desynchronization of thermosensitive neurons by using energy pumping., 602:127644. https://doi.org/10.1016/j.physa.2022.127644
He GG, Cao ZT, Chen HP, et al., 2003. Controlling chaos in a neural network based on the phase space constraint., 17(22n24):?4209-4214. https://doi.org/10.1142/S0217979203022192
He ZW, Yao CG, 2020. The effect of oxygen concentration on the coupled neurons: rich spiking patterns and synchronization., 63(11):2339-2348. https://doi.org/10.1007/s11431-020-1659-y
Hemby SE, Ginsberg SD, Brunk B, et al., 2002. Gene expression profile for schizophrenia: discrete neuron transcription patterns in the entorhinal cortex., 59(7):631-640. https://doi.org/10.1001/archpsyc.59.7.631
Hens C, Pal P, Dana SK, 2015. Bursting dynamics in a population of oscillatory and excitable Josephson junctions., 92(2):022915. https://doi.org/10.1103/PhysRevE.92.022915
Heras R, 2016. The Helmholtz theorem and retarded fields., 37(7):065204. https://doi.org/10.1088/0143-0807/37/6/065204
Hu YF, Zhang Y, Chang YL, et al., 2010. Optimizing the power output of a ZnO photocell by piezopotential., 4(7):4220-4224. https://doi.org/10.1021/nn1010045
Huang CL, Huang XQ, Zhang XM, et al., 2020. Waves induced by heterogeneity in oscillatory media., 22(8):083019. https://doi.org/10.1088/1367-2630/aba022
Ibarz B, Cao H, Sanjuán MAF, 2008. Bursting regimes in map-based neuron models coupled through fast threshold modulation., 77(5):051918. https://doi.org/10.1103/PhysRevE.77.051918
Jha MK, Morrison BM, 2018. Glia-neuron energy metabolism in health and diseases: new insights into the role of nervous system metabolic transporters., 309:23-31. https://doi.org/10.1016/j.expneurol.2018.07.009
Joglekar YN, Wolf SJ, 2009. The elusive memristor: properties of basic electrical circuits., 30(4):661-675. https://doi.org/10.1088/0143-0807/30/4/001
Kafraj MS, Parastesh F, Jafari S, 2020. Firing patterns of an improved Izhikevich neuron model under the effect of electromagnetic induction and noise., 137:109782. https://doi.org/10.1016/j.chaos.2020.109782
Khakh BS, 2019. Astrocyte–neuron interactions in the striatum: insights on identity, form, and function., 42(9):617-630. https://doi.org/10.1016/j.tins.2019.06.003
Kim KM, Yang JJ, Merced E, et al., 2015. Low variability resistor–memristor circuit masking the actual memristor states., 1(6):1500095. https://doi.org/10.1002/aelm.201500095
Kobe DH, 1986. Helmholtz's theorem revisited., 54(6):552-554. https://doi.org/10.1119/1.14562
Kuhtz-Buschbeck JP, Schaefer J, Wilder N, et al., 2021. The origin of the heartbeat and theories of muscle contraction. Physiological concepts and conflicts in the 19th century., 159:3-9. https://doi.org/10.1016/j.pbiomolbio.2020.05.009
Kyprianidis IM, Papachristou V, Stouboulos IN, et al., 2012. Dynamics of coupled chaotic Bonhoeffer-van der Pol oscillators., 11(9):516-526.
Latorre MA, W?rdell K, 2019. A comparison between single and double cable neuron models applicable to deep brain stimulation., 5(5):025026. https://doi.org/10.1088/2057-1976/aafdd9
Li J, Tang J, Ma J, et al., 2016. Dynamic transition of neuronal firing induced by abnormal astrocytic glutamate oscillation., 6:32343. https://doi.org/10.1038/srep32343
Li JJ, Liu SB, Liu WM, et al., 2016. Suppression of firing activities in neuron and neurons of network induced by electromagnetic radiation., 83(1-2):801-810. https://doi.org/10.1007/s11071-015-2368-7
Li JJ, Xie Y, Yu YG, et al., 2017. A neglected GABAergic astrocyte: calcium dynamics and involvement in seizure activity., 60(7):1003-1010. https://doi.org/10.1007/s11431-016-9056-2
Li KX, Bao H, Li HZ, et al., 2022. Memristive Rulkov neuron model with magnetic induction effects., 18(3):1726-1736. https://doi.org/10.1109/TII.2021.3086819
Li Y, Oku M, He GG, et al., 2017. Elimination of spiral waves in a locally connected chaotic neural network by a dynamic phase space constraint., 88:9-21. https://doi.org/10.1016/j.neunet.2017.01.002
Lin HR, Wang CH, Deng QL, et al., 2021. Review on chaotic dynamics of memristive neuron and neural network., 106(1):959-973. https://doi.org/10.1007/s11071-021-06853-x
Liu G, Guo L, Liu CL, et al., 2018. Evaluation of different calibration equations for NTC thermistor applied to high-precision temperature measurement., 120:21-27. https://doi.org/10.1016/j.measurement.2018.02.007
Liu Y, Xu WJ, Ma J, et al., 2020. A new photosensitive neuron model and its dynamics., 21(9):1387-1396. https://doi.org/10.1631/FITEE.1900606
Liu ZL, Wang CN, Jin WY, et al., 2019a. Capacitor coupling induces synchronization between neural circuits., 97(4):2661-2673. https://doi.org/10.1007/s11071-019-05155-7
Liu ZL, Wang CN, Zhang G, et al., 2019b. Synchronization between neural circuits connected by hybrid synapse., 33(16):1950170. https://doi.org/10.1142/S0217979219501704
Liu ZL, Zhou P, Ma J, et al., 2020. Autonomic learning via saturation gain method, and synchronization between neurons., 131:109533. https://doi.org/10.1016/j.chaos.2019.109533
Lu LL, Jia Y, Kirunda JB, et al., 2019. Effects of noise and synaptic weight on propagation of subthreshold excitatory postsynaptic current signal in a feed-forward neural network., 95(2):1673-1686. https://doi.org/10.1007/s11071-018-4652-9
Luo XS, 1999. Using phase space compression to control chaos and hyperchaos., 48(3):402-407 (in Chinese). https://doi.org/10.7498/aps.48.402
Lv M, Wang CN, Ren GD, et al., 2016. Model of electrical activity in a neuron under magnetic flow effect., 85(3):1479-1490. https://doi.org/10.1007/s11071-016-2773-6
Lv M, Ma J, Yao YG, et al., 2019. Synchronization and wave propagation in neuronal network under field coupling., 62(3):448-457. https://doi.org/10.1007/s11431-018-9268-2
Ma J, 2022. Chaos theory and applications: the physical evidence, mechanism are important in chaotic systems., 4(1):1-3.
Ma J, Tang J, 2017. A review for dynamics in neuron and neuronal network., 89(3):1569-1578. https://doi.org/10.1007/s11071-017-3565-3
Ma J, Wang QY, Jin WY, et al., 2008. Control chaos in Hindmarsh-Rose neuron by using intermittent feedback with one variable., 25(10):3582-3585. https://doi.org/10.1088/0256-307X/25/10/017
Ma J, Jia Y, Yi M, et al., 2009. Suppression of spiral wave and turbulence by using amplitude restriction of variable in a local square area., 41(3):1331-1339. https://doi.org/10.1016/j.chaos.2008.05.014
Ma J, Song XL, Jin WY, et al., 2015a. Autapse-induced synchronization in a coupled neuronal network., 80:31-38.
Ma J, Song XL, Tang J, et al., 2015b. Wave emitting and propagation induced by autapse in a forward feedback neuronal network., 167:378-389. https://doi.org/10.1016/j.neucom.2015.04.056
Ma J, Wu FQ, Hayat T, et al., 2017. Electromagnetic induction and radiation-induced abnormality of wave propagation in excitable media., 486:508-516. https://doi.org/10.1016/j.physa.2017.05.075
Ma J, Yang ZQ, Yang LJ, et al., 2019. A physical view of computational neurodynamics., 20(9):??639-659. https://doi.org/10.1631/jzus.A1900273
Ma SY, Yao Z, Zhang Y, et al., 2019. Phase synchronization and lock between memristive circuits under field coupling., 105:177-185. https://doi.org/10.1016/j.aeue.2019.04.018
Ma XW, Xu Y, 2022. Taming the hybrid synapse under energy balance between neurons., 159:112149. https://doi.org/10.1016/j.chaos.2022.112149
Majhi S, Perc M, Ghosh D, 2022. Dynamics on higher-order networks: a review., 19(188):20220043. https://doi.org/10.1098/rsif.2022.0043
Malik SA, Mir AH, 2020. FPGA realization of fractional order neuron., 81:372-385. https://doi.org/10.1016/j.apm.2019.12.008
Manor Y, Nadim F, 2001. Frequency regulation demonstrated by coupling a model and a biological neuron., 38-40:269-278. https://doi.org/10.1016/S0925-2312(01)00394-0
Matsubara T, Torikai H, Hishiki T, 2011. A generalized rotate-and-fire digital spiking neuron model and its on-FPGA learning., 58(10):677-681. https://doi.org/10.1109/TCSII.2011.2161705
Mishra A, Ghosh S, Kumar Dana S, et al., 2021. Neuron-like spiking and bursting in Josephson junctions: a review., 31(5):052101. https://doi.org/10.1063/5.0050526
Mishra D, Yadav A, Ray S, et al., 2006. Exploring biological neuron models., 7:13-22.
Mondal A, Upadhyay RK, Ma J, et al., 2019a. Bifurcation analysis and diverse firing activities of a modified excitable neuron model., 13(4):393-407. https://doi.org/10.1007/s11571-019-09526-z
Mondal A, Sharma SK, Upadhyay RK, et al., 2019b. Firing activities of a fractional-order FitzHugh-Rinzel bursting neuron model and its coupled dynamics., 9(1):15721. https://doi.org/10.1038/s41598-019-52061-4
Mostaghimi S, Nazarimehr F, Jafari S, et al., 2019. Chemical and electrical synapse-modulated dynamical properties of coupled neurons under magnetic flow., 348:42-56. https://doi.org/10.1016/j.amc.2018.11.030
Moujahid A, d'Anjou A, Torrealdea FJ, et al., 2011. Energy and information in Hodgkin-Huxley neurons., 83(3):031912. https://doi.org/10.1103/PhysRevE.83.031912
Mukamel R, Ekstrom AD, Kaplan J, et al., 2010. Single-neuron responses in humans during execution and observation of actions., 20(8):750-756. https://doi.org/10.1016/j.cub.2010.02.045
Muni SS, Rajagopal K, Karthikeyan A, et al., 2022. Discrete hybrid Izhikevich neuron model: nodal and network behaviours considering electromagnetic flux coupling., 155:111759. https://doi.org/10.1016/j.chaos.2021.111759
Nasiraee M, Kordy HM, Kazemitabar J, 2022. Capacity per unit cost-achieving input distribution of rated-inverse gaussian biological neuron., 70(6):3788-3803. https://doi.org/10.1109/TCOMM.2022.3168704
Nazari S, Amiri M, Faez K, et al., 2015. Multiplier-less digital implementation of neuron?–?astrocyte signalling on FPGA., 164:281-292. https://doi.org/10.1016/j.neucom.2015.02.041
Nenova ZP, Nenov TG, 2009. Linearization circuit of the thermistor connection., 58(2):441-449. https://doi.org/10.1109/TIM.2008.2003320
Njitacke ZT, Takembo CN, Koumetio BN, et al., 2022. Complex dynamics and autapse-modulated information patterns in memristive Wilson neurons., 110: 2793-2804. https://doi.org/10.1007/s11071-022-07738-3.
Nouri M, Hayati M, Serrano-Gotarredona T, et al., 2019. A digital neuromorphic realization of the 2-D Wilson neuron model., 66(1):136-140. https://doi.org/10.1109/TCSII.2018.2852598
Olumodeji OA, Gottardi M, 2017. Arduino-controlled HP memristor emulator for memristor circuit applications., 58:438-445. https://doi.org/10.1016/j.vlsi.2017.03.004
Pal K, Ghosh D, Gangopadhyay G, 2021. Synchronization and metabolic energy consumption in stochastic Hodgkin-Huxley neurons: patch size and drug blockers., 422:222-234. https://doi.org/10.1016/j.neucom.2020.10.006
Parastesh F, Jafari S, Azarnoush H, et al., 2021. Chimeras., 898:1-114. https://doi.org/10.1016/j.physrep.2020.10.003
Paul Asir M, Prasad A, Kuznetsov NV, et al., 2021. Chimera states in a class of hidden oscillatory networks., 104(2):1645-1655. https://doi.org/10.1007/S11071-021-06355-W
Peng L, Tang J, Ma J, et al., 2022. The influence of autapse on synchronous firing in small-world neural networks., 594:126956. https://doi.org/10.1016/j.physa.2022.126956
Peng YX, Sun KH, He SB, 2020. A discrete memristor model and its application in Hénon map., 137:109873. https://doi.org/10.1016/j.chaos.2020.109873
Pinto RD, Varona P, Volkovskii AR, et al., 2000. Synchronous behavior of two coupled electronic neurons., 62(2):2644-2656. https://doi.org/10.1103/PhysRevE.62.2644
Priya S, Song HC, Zhou Y, et al., 2017. A review on piezoelectric energy harvesting: materials, methods, and circuits., 4(1):3-39. https://doi.org/10.1515/ehs-2016-0028
Protachevicz PR, Iarosz KC, Caldas IL, et al., 2020. Influence of autapses on synchronization in neural networks with chemical synapses., 14:604563. https://doi.org/10.3389/fnsys.2020.604563
Qi CS, Li YY, Gu HG, et al., 2022. Nonlinear mechanism for the enhanced bursting activities induced by fast inhibitory autapse and reduced activities by fast excitatory autapse.,in press. https://doi.org/10.1007/s11571-022-09872-5
Qin HX, Wu Y, Wang CN, et al., 2015. Emitting waves from defects in network with autapses., 23(1-3):164-174. https://doi.org/10.1016/j.cnsns.2014.11.008
Radziemska E, Klugmann E, 2002. Thermally affected parameters of the current–voltage characteristics of silicon photocell., 43(14):?1889-1900. https://doi.org/10.1016/S0196-8904(01)00132-7
Rajagopal K, He SB, Karthikeyan A, et al., 2021. Size matters: effects of the size of heterogeneity on the wave re-entry and spiral wave formation in an excitable media., 31(5):053131. https://doi.org/10.1063/5.0051010
Ramakrishnan B, Mehrabbeik M, Parastesh F, et al., 2022. A new memristive neuron map model and its network's dynamics under electrochemical coupling., 11(1):153. https://doi.org/10.3390/electronics11010153
Ren GD, Zhou P, Ma J, et al., 2017. Dynamical response of electrical activities in digital neuron circuit driven by autapse., 27(12):1750187. https://doi.org/10.1142/S0218127417501875
Ricci G, Volpi L, Pasquali L, et al., 2009. Astrocyte–neuron interactions in neurological disorders., 35(4):317-336. https://doi.org/10.1007/s10867-009-9157-9
Rostami Z, Jafari S, 2018. Defects formation and spiral waves in a network of neurons in presence of electromagnetic induction., 12(2):?235-254. https://doi.org/10.1007/s11571-017-9472-y
Rulkov NF, 2001. Regularization of synchronized chaotic bursts., 86(1):183-186. https://doi.org/10.1103/PhysRevLett.86.183
Sarasola C, Torrealdea FJ, d'Anjou A, et al., 2004. Energy balance in feedback synchronization of chaotic systems., 69(1):011606. https://doi.org/10.1103/PhysRevE.69.011606
Schmidt R, Basu A, Brinkman AW, 2004. Production of NTCR thermistor devices based on NiMn2O4+δ., 24(6):1233-1236. https://doi.org/10.1016/S0955-2219(03)00415-1
Segall K, LeGro M, Kaplan S, et al., 2017. Synchronization dynamics on the picosecond time scale in coupled Josephson junction neurons., 95(3):032220. https://doi.org/10.1103/PhysRevE.95.032220
Shi M, Wang ZH, 2014. Abundant bursting patterns of a fractional-order Morris?–?Lecar neuron model., 19(6):1956-1969. https://doi.org/10.1016/j.cnsns.2013.10.032
Shi WW, Zhang JY, Zhang ZG, et al., 2020. An introduction and review on innovative silicon implementations of implantable/scalp EEG chips for data acquisition, seizure/behavior detection, and brain stimulation., 6(3):242-254. https://doi.org/10.26599/BSA.2020.9050024
Si H, Sun XJ, 2021. Information propagation in recurrent neuronal populations with mixed excitatory-inhibitory synaptic connections., 104(1):557-576. https://doi.org/10.1007/s11071-020-06192-3
Silverman ME, Grove D, Upshaw CB, 2006. Why does the heart beat? The discovery of the electrical system of the heart., 113(23):2775-2781. https://doi.org/10.1161/CIRCULATIONAHA.106.616771
Song XL, Wang HT, Chen Y, 2019. Autapse-induced firing patterns transitions in the Morris-Lecar neuron model., 96(4):2341-2350. https://doi.org/10.1007/s11071-019-04925-7
Sugino C, Ruzzene M, Erturk A, 2020. Nonreciprocal piezoelectric metamaterial framework and circuit strategies., 102(1):014304. https://doi.org/10.1103/PhysRevB.102.014304
Sun XJ, Si H, 2020. Population rate coding in recurrent neuronal networks consisting of neurons with mixed excitatory–inhibitory synapses., 100(3):?2673-2686. https://doi.org/10.1007/s11071-020-05653-z
Taher H, Avitabile D, Desroches M, 2022. Bursting in a next generation neural mass model with synaptic dynamics: a slow-fast approach., 108(4):?4261-4285. https://doi.org/10.1007/s11071-022-07406-6
Teka WW, Upadhyay RK, Mondal A, 2018. Spiking and bursting patterns of fractional-order Izhikevich model., 56:161-176. https://doi.org/10.1016/j.cnsns.2017.07.026
Telesford QK, Lynall ME, Vettel J, et al., 2016. Detection of functional brain network reconfiguration during task-driven cognitive states., 142:198-210. https://doi.org/10.1016/j.neuroimage.2016.05.078
Tomimatsu A, Yokokura S, Awaga K, 2022. Duty-cycle dependence of photo-induced displacement current in MISIM photocells., 109:106632. https://doi.org/10.1016/j.orgel.2022.106632
Torrealdea FJ, d'Anjou A, Gra?a M, et al., 2006. Energy aspects of the synchronization of model neurons., 74(1):011905. https://doi.org/10.1103/PhysRevE.74.011905
Torrealdea FJ, Sarasola C, d'Anjou A, 2009. Energy consumption and information transmission in model neurons., 40(1):60-68. https://doi.org/10.1016/j.chaos.2007.07.050
Trenchard H, Perc M, 2016. Energy saving mechanisms, collective behavior and the variation range hypothesis in biological systems: a review., 147:40-66. https://doi.org/10.1016/j.biosystems.2016.05.010
Tuckwell HC, 2006. Spatial neuron model with two-parameter Ornstein?–?Uhlenbeck input current., 368(2):495-510. https://doi.org/10.1016/j.physa.2005.12.022
Tuo XH, Yang XL, 2022. How synaptic plasticity affects the stochastic resonance in a modular neuronal network?, 110(1):791-802. https://doi.org/10.1007/s11071-022-07620-2
Turrigiano G, 2012. Homeostatic synaptic plasticity: local and global mechanisms for stabilizing neuronal function., 4(1):a005736. https://doi.org/10.1101/cshperspect.a005736
Upadhyay RK, Sharma SK, Mondal A, et al., 2022. Emergence of hidden dynamics in different neuronal network architecture with injected electromagnetic induction., 111:288-309. https://doi.org/10.1016/j.apm.2022.06.031
van Geit W, de Schutter E, Achard P, 2008. Automated neuron model optimization techniques: a review., 99(4):241-251. https://doi.org/10.1007/s00422-008-0257-6
Vecchio F, Miraglia F, Rossini PM, 2017. Connectome: graph theory application in functional brain network architecture., 2:206-213. https://doi.org/10.1016/j.cnp.2017.09.003
Wang CN, Ma J, 2018. A review and guidance for pattern selection in spatiotemporal system., 32(6):1830003. https://doi.org/10.1142/S0217979218300037
Wang CN, Guo SL, Xu Y, et al., 2017. Formation of autapse connected to neuron and its biological function., 2017:5436737. https://doi.org/10.1155/2017/5436737
Wang CN, Tang J, Ma J, 2019. Minireview on signal exchange between nonlinear circuits and neurons via field coupling., 228(10):1907-1924. https://doi.org/10.1140/epjst/e2019-800193-8
Wang CN, Sun GP, Yang FF, et al., 2022. Capacitive coupling memristive systems for energy balance., 153:154280. https://doi.org/10.1016/J.AEUE.2022.154280
Wang R, Lin P, Liu MX, et al., 2019. Hierarchical connectome modes and critical state jointly maximize human brain fun ctional diversity., 123(3):038301. https://doi.org/10.1103/PhysRevLett.123.038301
Wang Y, Ma J, 2022. Creation of synaptic connection to memristive neurons under noise., 270:170011. https://doi.org/10.1016/j.ijleo.2022.170011
Wang Y, Sun GP, Ren GD, 2022. Diffusive field coupling induced synchronization between neural circuits under energy balance.,in press. https://doi.org/10.1088/1674-1056/ac7bff
Wu FQ, Wang CN, Xu Y, et al., 2016. Model of electrical activity in cardiac tissue under electromagnetic induction., 6(1):28. https://doi.org/10.1038/s41598-016-0031-2
Wu FQ, Wang CN, Jin WY, et al., 2017. Dynamical responses in a new neuron model subjected to electromagnetic induction and phase noise., 469:81-88. https://doi.org/10.1016/j.physa.2016.11.056
Wu FQ, Gu HG, Jia YB, 2021. Bifurcations underlying different excitability transitions modulated by excitatory and inhibitory memristor and chemical autapses., 153:111611. https://doi.org/10.1016/J.CHAOS.2021.111611
Xie Y, Ma J, 2022. How to discern external acoustic waves in a piezoelectric neuron under noise?, 48(3):339-353. https://doi.org/10.1007/s10867-022-09611-1
Xie Y, Zhu ZG, Zhang XF, et al., 2021a. Control of firing mode in nonlinear neuron circuit driven by photocurrent., 70(21):210502 (in Chinese). https://doi.org/10.7498/aps.70.20210676
Xie Y, Yao Z, Hu XK, et al., 2021b. Enhance sensitivity to illumination and synchronization in light-dependent neurons., 30(12):120510. https://doi.org/10.1088/1674-1056/ac1fdc
Xie Y, Yao Z, Ma J, 2022a. Formation of local heterogeneity under energy collection in neural networks.,in press. https://doi.org/10.1007/s11431-022-2188-2
Xie Y, Yao Z, Ma J, 2022b. Phase synchronization and energy balance between neurons., 23(9):1407-1420. https://doi.org/10.1631/FITEE.2100563
Xie Y, Zhou P, Yao Z, et al., 2022c. Response mechanism in a functional neuron under multiple stimuli., 607:128175. https://doi.org/10.1016/j.physa.2022.128175
Xie Y, Zhou P, Ma J, 2023. Energy balance and synchronization via inductive-coupling in functional neural circuits., 113:175-187. https://doi.org/10.1016/j.apm.2022.09.015
Xu KS, Maidana JP, Orio P, 2021. Diversity of neuronal activity is provided by hybrid synapses., 105(3):2693-2710. https://doi.org/10.1007/s11071-021-06704-9
Xu Y, Ma J, 2022. Pattern formation in a thermosensitive neural network., 111:106426. https://doi.org/10.1016/j.cnsns.2022.106426
Xu Y, Ying HP, Jia Y, et al., 2017. Autaptic regulation of electrical activities in neuron under electromagnetic induction., 7:43452. https://doi.org/10.1038/srep43452
Xu Y, Jia Y, Ma J, et al., 2018a. Collective responses in electrical activities of neurons under field coupling., 8(1):1349. https://doi.org/10.1038/s41598-018-19858-1
Xu Y, Jia Y, Ge MY, et al., 2018b. Effects of ion channel blocks on electrical activity of stochastic Hodgkin–Huxley neural network under electromagnetic induction., 283:196-204. https://doi.org/10.1016/j.neucom.2017.12.036
Xu Y, Jia Y, Wang HW, et al., 2019. Spiking activities in chain neural network driven by channel noise with field coupling., 95(4):3237-3247. https://doi.org/10.1007/s11071-018-04752-2
Xu Y, Guo YY, Ren GD, et al., 2020. Dynamics and stochastic resonance in a thermosensitive neuron., 385:125427. https://doi.org/10.1016/j.amc.2020.125427
Xu YM, Yao Z, Hobiny A, et al., 2019. Differential coupling contributes to synchronization via a capacitor connection between chaotic circuits., 20(4):571-583. https://doi.org/10.1631/FITEE.1800499
Yakovleva M, Bhand S, Danielsson B, 2013. The enzyme thermistor?–?a realistic biosensor concept. A critical review., 766:1-12. http://dx.doi.org/10.1016/j.aca.2012.12.004
Yan XC, Yang DP, Lin ZH, et al., 2022. Significant low-dimensional spectral-temporal features for seizure detection., 30:668-677. https://doi.org/10.1109/TNSRE.2022.3156931
Yang J, Sawan M, 2020. From seizure detection to smart and fully embedded seizure prediction engine: a review., 14(5):1008-1023. https://doi.org/10.1109/TBCAS.2020.3018465
Yang XL, Wang JY, Sun ZK, 2017. The collective bursting dynamics in a modular neuronal network with synaptic plasticity., 89(4):2593-2602. https://doi.org/10.1007/s11071-017-3606-y
Yao CG, He ZW, Nakano T, et al., 2019. Inhibitory-autapse-enhanced signal transmission in neural networks., 97(2):1425-1437. https://doi.org/10.1007/s11071-019-05060-z
Yao Z, Wang CN, 2021. Control the collective behaviors in a functional neural network., 152:111361. https://doi.org/10.1016/j.chaos.2021.111361
Yao Z, Wang CN, 2022. Collective behaviors in a multiple functional network with hybrid synapses., 605:127981. https://doi.org/10.1016/j.physa.2022.127981
Yao Z, Zhou P, Zhu ZG, et al., 2021a. Phase synchronization between a light-dependent neuron and a thermosensitive neuron., 423:518-534. https://doi.org/10.1016/j.neucom.2020.09.083
Yao Z, Wang CN, Zhou P, et al., 2021b. Regulating synchronous patterns in neurons and networks via field coupling., 95:105583. https://doi.org/10.1016/j.cnsns.2020.105583
Yilmaz E, Baysal V, Ozer M, et al., 2016. Autaptic pacemaker mediated propagation of weak rhythmic activity across small-world neuronal networks., 444:538-546. https://doi.org/10.1016/j.physa.2015.10.054
Yu HT, Wang J, Sun JB, et al., 2012. Effects of hybrid synapses on the vibrational resonance in small-world neuronal networks., 22(3):033105. https://doi.org/10.1063/1.4729462
Yu HT, Guo XM, Wang J, 2017. Stochastic resonance enhancement of small-world neural networks by hybrid synapses and time delay., 42:532-544. https://doi.org/10.1016/j.cnsns.2016.06.021
Yu K, Niu XD, Krook-Magnuson E, et al., 2021. Intrinsic functional neuron-type selectivity of transcranial focused ultrasound neuromodulation., 12(1):2519. https://doi.org/10.1038/S41467-021-22743-7
Yu YY, Li JJ, Yuan ZX, et al., 2022. Dynamic mechanism of epileptic seizures generation and propagation after ischemic stroke., 109(4):3113-3132. https://doi.org/10.1007/s11071-022-07577-2
Yuan Y, Huo H, Fang T, 2018. Effects of metabolic energy on synaptic transmission and dendritic integration in pyramidal neurons., 12:79. https://doi.org/10.3389/fncom.2018.00079
Yuan ZX, Feng PH, Du MM, et al., 2020. Dynamical response of a neuron?–astrocyte coupling system under electromagnetic induction and external stimulation., 29(3):030504. https://doi.org/10.1088/1674-1056/ab7441
Zamen S, Dehghan-Niri E, 2019. Observation and diagnosis of chaos in nonlinear acoustic waves using phase-space domain., 463:114959. https://doi.org/10.1016/j.jsv.2019.114959
Zhang G, Ma J, Alsaedi A, et al., 2018a. Dynamical behavior and application in Josephson junction coupled by memristor., 321:?290-299. https://doi.org/10.1016/j.amc.2017.10.054
Zhang G, Wu FQ, Hayat T, et al., 2018b. Selection of spatial pattern on resonant network of coupled memristor and Josephson junction., 65:79-90. https://doi.org/10.1016/j.cnsns.2018.05.018
Zhang X, Shen K, 2001. Controlling spatiotemporal chaos via phase space compression., 63(4):046212. https://doi.org/10.1103/PhysRevE.63.046212
Zhang XF, Ma J, 2021. Wave filtering and firing modes in a light-sensitive neural circuit., 22(9):?707-720. https://doi.org/10.1631/jzus.A2100323
Zhang XF, Wang CN, Ma J, et al., 2020. Control and synchronization in nonlinear circuits by using a thermistor., 34(25):2050267. https://doi.org/10.1142/S021798492050267X
Zhang XF, Ma J, Xu Y, et al., 2021a. Synchronization between FitzHugh-Nagumo neurons coupled with phototube., 70(9):090502 (in Chinese). https://doi.org/10.7498/aps.70.20201953
Zhang XF, Yao Z, Guo YY, et al., 2021b. Target wave in the network coupled by thermistors., 142:110455. https://doi.org/10.1016/J.CHAOS.2020.110455
Zhang Y, Xu Y, Yao Z, et al., 2020a. A feasible neuron for estimating the magnetic field effect., 102(3):1849-1867. https://doi.org/10.1007/s11071-020-05991-y
Zhang Y, Wang CN, Tang J, et al., 2020b. Phase coupling synchronization of FHN neurons connected by a Josephson junction., 63(11):2328-2338. https://doi.org/10.1007/s11431-019-1547-5
Zhang Y, Zhou P, Tang J, et al., 2021. Mode selection in a neuron driven by Josephson junction current in presence of magnetic field., 71:72-84. https://doi.org/10.1016/j.cjph.2020.11.011
Zhao ZG, Li L, Gu HG, 2020. Excitatory autapse induces different cases of reduced neuronal firing activities near Hopf bifurcation., 85:105250. https://doi.org/10.1016/j.cnsns.2020.105250
Zhou P, Yao Z, Ma J, et al., 2021a. A piezoelectric sensing neuron and resonance synchronization between auditory neurons under stimulus., 145:110751. https://doi.org/10.1016/j.chaos.2021.110751
Zhou P, Hu XK, Zhu ZG, et al., 2021b. What is the most suitable Lyapunov function?, 150:111154. https://doi.org/10.1016/j.chaos.2021.111154
Zhou P, Zhang XF, Ma J, 2022a. How to wake up the electric synapse coupling between neurons?, 108(2):1681-1695. https://doi.org/10.1007/s11071-022-07282-0
Zhou P, Zhang XF, Hu XK, et al., 2022b. Energy balance between two thermosensitive circuits under field coupling., 110(2):1879-1895. https://doi.org/10.1007/s11071-022-07669-z
Zhou Q, Wei DQ, 2021. Collective dynamics of neuronal network under synapse and field coupling., 105(1):753-765. https://doi.org/10.1007/s11071-021-06575-0
Zhu ZG, Ren GD, Zhang XF, et al., 2021. Effects of multiplicative-noise and coupling on synchronization in thermosensitive neural circuits., 151:111203. https://doi.org/10.1016/j.chaos.2021.111203
Oct. 4, 2022;
Revision accepted Oct. 27, 2022;
Crosschecked Nov. 22, 2022;
Online first Dec. 23, 2022
? Zhejiang University Press 2022
 Journal of Zhejiang University-Science A(Applied Physics & Engineering)2023年2期
Journal of Zhejiang University-Science A(Applied Physics & Engineering)2023年2期
- Journal of Zhejiang University-Science A(Applied Physics & Engineering)的其它文章
- Deformation pre-compensated optimization design of cam ring for low pulsation hydraulic motors
- Advanced ocean wave energy harvesting: current progress and future trends
- Reliability measure approach considering mixture uncertainties under insufficient input data
- Preparation and 3D printing of high-thermal-conductivity continuous mesophase-pitch-based carbon fiber/epoxy composites
