逯婧瑜,閆喜紅,b*,郭思怡

(太原師范學(xué)院 a.數(shù)學(xué)與統(tǒng)計(jì)學(xué)院;b.智能優(yōu)化計(jì)算與區(qū)塊鏈技術(shù)山西省重點(diǎn)實(shí)驗(yàn)室,山西 晉中 030619)

0 引言

近年來(lái),我國(guó)的民航事業(yè),包括航空企業(yè)的旅客運(yùn)輸量和機(jī)場(chǎng)建設(shè)方面,都取得了很大的進(jìn)步.到2020年年底,我國(guó)國(guó)內(nèi)已經(jīng)頒證的民用航空機(jī)場(chǎng)共241個(gè),如何保護(hù)如此龐大的國(guó)內(nèi)機(jī)場(chǎng)網(wǎng)絡(luò)[1]是一項(xiàng)具有挑戰(zhàn)性的任務(wù).

目前,國(guó)內(nèi)外針對(duì)機(jī)場(chǎng)安全的研究有很多.比如,對(duì)機(jī)場(chǎng)安全風(fēng)險(xiǎn)評(píng)估中存在的問(wèn)題繼續(xù)進(jìn)行優(yōu)化設(shè)計(jì)[2];對(duì)機(jī)場(chǎng)安全運(yùn)行機(jī)制進(jìn)行分析[3];對(duì)機(jī)場(chǎng)凈空障礙物進(jìn)行分析測(cè)量[4];對(duì)多目標(biāo)的機(jī)場(chǎng)停機(jī)位的預(yù)警分配模型的構(gòu)建[5]等.但是針對(duì)國(guó)內(nèi)機(jī)場(chǎng)網(wǎng)絡(luò)的整體安全保護(hù)的研究較少,Yan等[6]針對(duì)同一類(lèi)型的恐怖分子襲擊國(guó)內(nèi)機(jī)場(chǎng)網(wǎng)絡(luò)資源配置問(wèn)題,建立了雙層優(yōu)化模型,其中上層模型為政府向各機(jī)場(chǎng)提供預(yù)算分配,下層模型是恐怖分子選擇一個(gè)航班進(jìn)行攻擊,從而使預(yù)期損失最大化,并采用了割平面算法來(lái)求解此雙層優(yōu)化問(wèn)題,同時(shí)進(jìn)行了敏感性分析.

為了提高國(guó)內(nèi)機(jī)場(chǎng)網(wǎng)絡(luò)安全性,在Yan等[6]的研究基礎(chǔ)上,考慮到實(shí)際情況中恐怖分子類(lèi)型多種多樣,不同能力的恐怖分子通過(guò)機(jī)場(chǎng)的概率不同,從而建立針對(duì)多種類(lèi)型恐怖分子的保護(hù)國(guó)內(nèi)機(jī)場(chǎng)網(wǎng)絡(luò)安全的預(yù)算分配模型,并采用松弛割平面算法來(lái)求解該模型.

1 問(wèn)題描述及模型建立

以下將研究如何有效地將資源分配給國(guó)內(nèi)機(jī)場(chǎng),以保障整個(gè)機(jī)場(chǎng)網(wǎng)絡(luò).事先政府會(huì)確定分配給每個(gè)機(jī)場(chǎng)的預(yù)算數(shù)額,并估計(jì)恐怖分子成功通過(guò)各個(gè)機(jī)場(chǎng)的概率,從而提出一個(gè)雙層優(yōu)化模型[6],其中政府是領(lǐng)導(dǎo)者,恐怖分子是追隨者.恐怖分子會(huì)通過(guò)情報(bào)獲取其成功通過(guò)率等信息,在預(yù)算有限的情況下,決定采取選用哪類(lèi)方式對(duì)哪些航班段進(jìn)行攻擊.恐怖分子的目標(biāo)是將預(yù)期損失最大化,而政府的目標(biāo)是將恐怖分子造成的最大預(yù)期損失最小化.參數(shù)設(shè)置如下表1.

表1 問(wèn)題模型符號(hào)列表

下面定義決策變量:

設(shè)x,y分別是xi,yjljk對(duì)應(yīng)的向量和矩陣,根據(jù)上述引入的參數(shù)和決策變量,建立如下雙層優(yōu)化模型:

(1)

(2)

(3)

yjljk∈{0,1}, ?j∈J,k∈K,lj∈{1,…,nj},

(4)

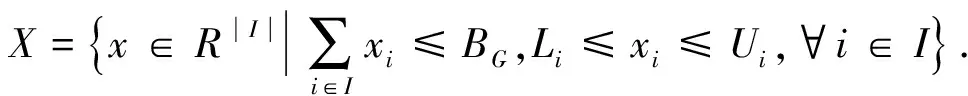
在上層優(yōu)化中,政府希望在預(yù)防恐怖分子襲擊事件時(shí)使得預(yù)計(jì)產(chǎn)生的損失W減少到最小.集合X可以保證國(guó)內(nèi)所有機(jī)場(chǎng)獲得的政府分配的預(yù)算值總數(shù)在政府計(jì)劃限額BG之內(nèi),同時(shí)也可以保證具體到每一個(gè)機(jī)場(chǎng)的預(yù)算分配也在相應(yīng)規(guī)定的范圍內(nèi).在下層優(yōu)化中,恐怖分子也希望能通過(guò)制定最佳的攻擊方案從而將可能造成的破壞提升到最大.約束條件(2)保證了恐怖分子只能選擇一趟航班中的其中一個(gè)航班段進(jìn)行攻擊.約束條件(3)保證了恐怖分子預(yù)設(shè)的攻擊成本在其合理的計(jì)劃限額BT之內(nèi)的.

2 松弛割平面算法

對(duì)于上述雙層優(yōu)化模型,采用松弛割平面算法.松弛割平面算法是目前針對(duì)大規(guī)模0-1整數(shù)規(guī)劃問(wèn)題的一種有效求解算法[7].相比于割平面算法可以使大規(guī)模問(wèn)題在很短的時(shí)間內(nèi)得到一個(gè)較好的解.

該算法流程如下:

松弛割平面算法

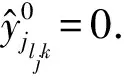
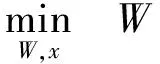
(5)

(6)

(7)

Li≤xi≤Ui, ?i∈I.

(8)

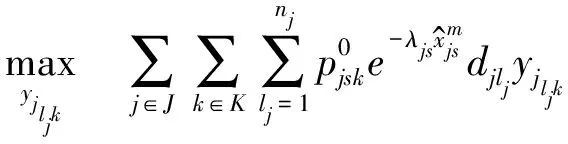
(9)

(10)

(11)

yjljk∈[0,1], ?j∈J,k∈K,lj∈{1,…,nj}.

(12)

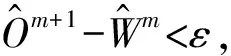
3 數(shù)值實(shí)驗(yàn)

為了驗(yàn)證所提出算法的有效性,將利用松弛割平面算法做了大量數(shù)值實(shí)驗(yàn),如下表2.所有的算法用MATLAB(R2019b)編寫(xiě).下面考慮10個(gè)機(jī)場(chǎng)所構(gòu)成的機(jī)場(chǎng)網(wǎng)絡(luò).取政府的總預(yù)算均為20萬(wàn)元,恐怖分子的總預(yù)算為50萬(wàn)元,雇傭第1類(lèi)恐怖分子費(fèi)用為20萬(wàn)元,雇傭第2類(lèi)恐怖分子類(lèi)型為30萬(wàn)元,其余數(shù)值隨機(jī)生成.通過(guò)將航班數(shù)從50增加到240,驗(yàn)證了算法的有效性.不同規(guī)模問(wèn)題的實(shí)驗(yàn)結(jié)果表明,所提出的松弛割平面算法能在合理的時(shí)間內(nèi)取得較為滿意的可行解.

表2 松弛割平面算法數(shù)值結(jié)果

4 小結(jié)

在文獻(xiàn)[6]研究基礎(chǔ)上,針對(duì)不同類(lèi)型的恐怖分子襲擊國(guó)內(nèi)機(jī)場(chǎng)網(wǎng)絡(luò)資源配置問(wèn)題提出了0-1雙層整數(shù)規(guī)劃模型,并設(shè)計(jì)了松弛割平面算法.在該算法中,由于0-1整數(shù)規(guī)劃的特殊結(jié)構(gòu)和性質(zhì),為此將0-1決策變量yjljk松弛到閉區(qū)間[0,1]上,為求解針對(duì)國(guó)內(nèi)機(jī)場(chǎng)網(wǎng)絡(luò)安全的資源配置問(wèn)題提供了新角度和新思路.