王月卿, 林雅津

(1.閩南師范大學(xué) 計算機學(xué)院, 福建 漳州 363000; 2.閩南師范大學(xué) 數(shù)學(xué)與統(tǒng)計學(xué)院, 福建 漳州 363000)

等式成立當(dāng)且僅當(dāng)G?Sn.

本文討論的圖均為無向連通圖,設(shè)G=(V,E),其中V(G)為圖G的頂點集,其階數(shù)為n;E(G)為圖G的邊集,其階數(shù)為m;用dv表示與頂點v∈V(G)相關(guān)聯(lián)的的邊數(shù),稱為頂點v的度;頂點數(shù)為n的完全圖,星圖和路分別用Kn,Sn及Pn表示.

用q(G)表示無符號拉普拉斯矩陣Q(G)=D(G)+A(G)的譜半徑,即矩陣Q(G)的最大特征值,其中D(G)和A(G)分別為圖G的度對角矩陣和鄰接矩陣;用λ(G)表示圖G的譜半徑,即矩陣A(G)的最大特征值.

Zhou等[1]定義并研究了圖G的Sum-connectivity指標(biāo),其定義如下:

更多關(guān)于圖的Sum-connectivity指標(biāo)的性質(zhì),可參考文獻1～3.

對于簡單圖G,其性質(zhì)可以借助各種形式的圖的拓撲指標(biāo)來衡量,對其各自拓撲指標(biāo)的研究,目前已有大量的成果.近期,關(guān)于圖的特征值(特別是q(G)和λ(G))與圖的拓撲指標(biāo)之間關(guān)系的研究受到了廣泛關(guān)注.

本文主要研究的是χ(G)與q(G)之間的關(guān)系,證明了以下結(jié)論.

定理1設(shè)G為具有n≥3個頂點的連通圖,則

等號成立當(dāng)且僅當(dāng)G?Sn.

1 預(yù)備知識

首先,我們將給出一些在證明過程中將會用到的已有結(jié)論.在文獻4～5中分別給出了無符號拉普拉斯譜半徑和鄰接矩陣譜半徑的上界.

引理1.1[6]設(shè)G為具有n個頂點,m條邊的連通圖,則

等號成立當(dāng)且僅當(dāng)G?Kn或G?Sn.

引理1.2[7]設(shè)G為具有n個頂點,m條邊的連通圖,λ(G)為鄰接矩陣的譜半徑,則

等號成立當(dāng)且僅當(dāng)G?Kn或G?Sn.

引理1.3[8]設(shè)G為具有n個頂點的任意連通圖,λ(G)為鄰接矩陣的譜半徑,則

引理1.4[1]令G為具有m條邊的連通圖,則

引理1.5設(shè)G為具有n個頂點,m條邊的連通圖,則

證明由引理1.3和1.4,則

結(jié)論成立.

2 定理1的證明

在給出定理1的證明之前,首先證明以下事實,設(shè)G為具有n≥5個頂點,m條邊的連通圖,則有

引理2.1設(shè)G為具有n≥5個頂點,m條邊的簡單連通圖,則

證明因為G為簡單連通圖,所以有m≥n-1.以下將根據(jù)m的大小分兩種情況對引理2.1進行證明.

(1)當(dāng)m=n-1時

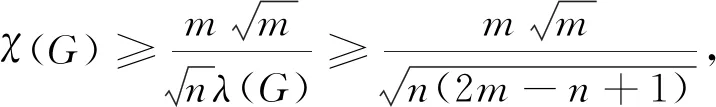
令

則

(1)

其中

g(m)=(m-n+1)[nm2+(n-4)(n-1)m-(n3-4n2+4n-2)].

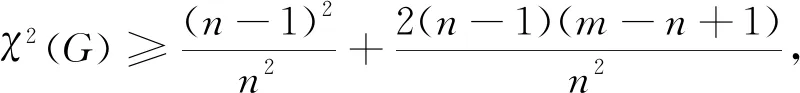
(2)當(dāng)時m≥n時

注意到

g(m)=(m-n+1)[nm2+(n-4)(n-1)m-(n3-4n2+4n-2)],

顯然

有g(shù)(m)≥0.

因為

所以有

綜上所述,當(dāng)m≥n-1時,有

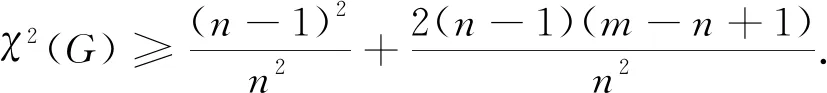
引理2.2設(shè)G為具有n≥5個頂點,m條邊的簡單連通圖.若

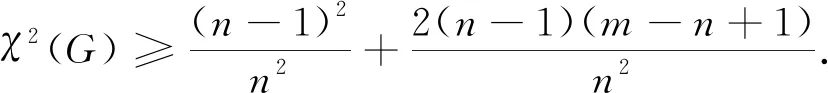
下面分兩種情況進行討論:

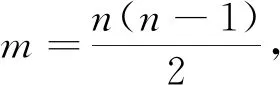
(2)當(dāng)G?Sn時,m=n-1,則有

由引理2.1和2.2,可得以下結(jié)論.

引理2.3設(shè)G為具有n≥5個頂點的簡單連通圖.則

等號成立當(dāng)且僅當(dāng)G?Sn.

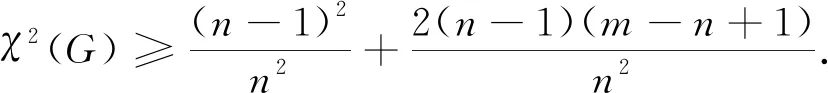
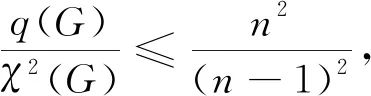
引理2.4設(shè)G為具有n=3個頂點的簡單連通圖.則

等號成立當(dāng)且僅當(dāng)G?S3.

表1 頂點數(shù)n=3

引理2.5設(shè)G為具有n=4個頂點的簡單連通圖.則

等式成立當(dāng)且僅當(dāng)G?S4.

表2 頂點數(shù)n=4

定理1的證明由引理2.3, 2.4, 2.5易得.