Observer-Based Path Tracking Controller Design for Autonomous Ground Vehicles With Input Saturation
Heng Wang, Tengfei Zhang, Xiaoyu Zhang, and Qing Li
Abstract—This paper investigates the problem of path tracking control for autonomous ground vehicles (AGVs), where the input saturation, system nonlinearities and uncertainties are considered.Firstly, the nonlinear path tracking system is formulated as a linear parameter varying (LPV) model where the variation of vehicle velocity is taken into account.Secondly, considering the noise effects on the measurement of lateral offset and heading angle, an observer-based control strategy is proposed, and by analyzing the frequency domain characteristics of the derivative of desired heading angle, a finite frequency H∞index is proposed to attenuate the effects of the derivative of desired heading angle on path tracking error.Thirdly, sufficient conditions are derived to guarantee robust H∞performance of the path tracking system,and the calculation of observer and controller gains is converted into solving a convex optimization problem.Finally, simulation examples verify the advantages of the control method proposed in this paper.
I.INTRODUCTION
IN the past two decades, autonomous ground vehicles(AGVs) have been studied extensively due to their potential advantages in driving behavior prediction, fuel consumption optimization, and traffic accident avoidance [1] and [2],etc.Among all critical tasks of AGVs, path tracking control is one of the key technologies, and guarantees that vehicles can follow predetermined paths stably [3] and [4].However, path tracking control of AGVs becomes a challenging problem when considering the effects of vehicle nonlinearities, uncertainties, actuator saturation, etc., which still deserves further investigation in the literature.
The linear parameter varying (LPV) model has advantages in dealing with complex nonlinear systems, and allows for control problem of nonlinear systems to be addressed by using mature linear control methods [5].In [6], the polytopic model is proposed to describe the variations of vehicle velocity, and an LPV system is constructed for path tracking of autonomous vehicles.In view of the uncertainties in vehicle load, velocity and tire cornering stiffness, an LPV model is constructed to obtain a quasi-linear system model, which is the basis for path tracking of autonomous vehicles [7].Plenty of control methods, such as model predictive control (MPC), LQR control,fuzzy control, and robustH∞control, have been utilized for achieving path tracking of autonomous vehicles.In [8], a novel MPC-based control strategy was designed for AGVs,where a path tracking controller was generated through the online optimization method.In [9], a lateral control algorithm was designed based on the fuzzy control strategy and sliding mode control (SMC) strategy, where fuzzy layers were used to ameliorate system chattering and improve control performance, and a sliding mode function was chosen to improve system robustness.In [10], a robust LQR controller with adaptive weights is proposed for AGVs with output constraints.In[11], a nonlinearH∞feedback control algorithm is proposed for a mobile vehicle with external disturbances, where the controller gain is obtained through solving certain Riccati equations.Note that the MPC and LQR methods stated above are based on accurate mathematical models.The SMC control method has a high degree of reliance on control parameters,and the selection of fuzzy rules depends on experience.They are difficult to use for path tracking control of AGVs due to their parametric nonlinearities and uncertainties.The robustH∞control method possesses advantages in suppressing external disturbances, which can effectively improve vehicle stability and path tracking performance [12].
In practice, disturbances usually occur in the finite frequency domain, and the attenuation of such finite frequency disturbance motivates so-called finite frequency controller design approaches [13] and [14].In [15], a finite frequencyH∞observer is designed to reduce estimation errors.In [16],by using the generalized Kalman-Yakubovic-Popov (GKYP)lemma, sufficient conditions in the forms of linear matrix inequalities (LMIs) are developed to guarantee finite frequencyH∞performance for T-S fuzzy systems.Note that the problem of input saturation has been studied extensively for different kinds of systems, for example, vehicle platoon control systems [17], unmanned aerial vehicles (UAVs) geofence systems [18], stochastic nonlinear systems [19], complex dynamical network (CDN) control systems [20], etc.For the practical implementation of AGV control, the required steering action cannot be generated ideally due to certain servomechanism limitations, i.e., actuator saturation, which may reduce path tracking accuracy or even lead to instability of the overall control system.To deal with this problem, the effect of input saturation is usually taken into account when designing path tracking control algorithms.In [21], an improved adaptive SMC controller is designed for lane-keeping problems of AGVs with actuator saturation.In [22], a robust yaw moment controller is proposed for an AGV in the presence of actuator saturation, where a polytopic method is proposed to deal with input saturation.In [23], a robustH∞dynamic output-feedback controller is designed for a four-wheel independently actuated electric ground vehicle, where parameter uncertainties, saturation, and faults are handled simultaneously.
To the best of our knowledge, frequency characteristics of desired heading angles for designing the path tracking controllers have not been well investigated in the literature.To deal with this problem, an observer-based path tracking controller is designed for AGVs with parametric nonlinearities,uncertainties and input saturation.The main contributions are summarized as follows.First, the nonlinear path tracking system of AGVs is converted into an LPV system with measurement noises, modeling errors and input saturation, which serves as a basis for the path tracking control of AGVs.Second, by analyzing the frequency characteristics of the desired heading angle, a finite frequencyH∞performance index is proposed to attenuate the effect of the derivative of desired heading angle on path tracking error, and a series of sufficient conditions are derived to guarantee the robustH∞performance of the path tracking system.Finally, the effectiveness and advantages of the proposed control strategy are verified through simulation results.
The structure of this paper is summarized as follows.In Section II, the path tracking problem is formulated for AGVs.In Section III, the main results of stability analysis and sufficient conditions of observer-based controller design are presented for path tracking of AGVs.Simulation results are proposed in Section IV, and some conclusions are summarized in Section V.
Notations:For a matrixP,PTrepresents its transpose,P?1represents its inverse,P⊥represents its orthogonal complement,P>0 and (P<0) represents the positive (negative) definiteness, He(P)=P+PT.I, 0, and * denote the identity matrix, zero matrix, and the symmetric term with appropriate dimension, respectively.C o{·} stands for a convex hull.
II.SYSTEM MODELING AND PROBLEM STATEMENT
A.Vehicle Dynamics
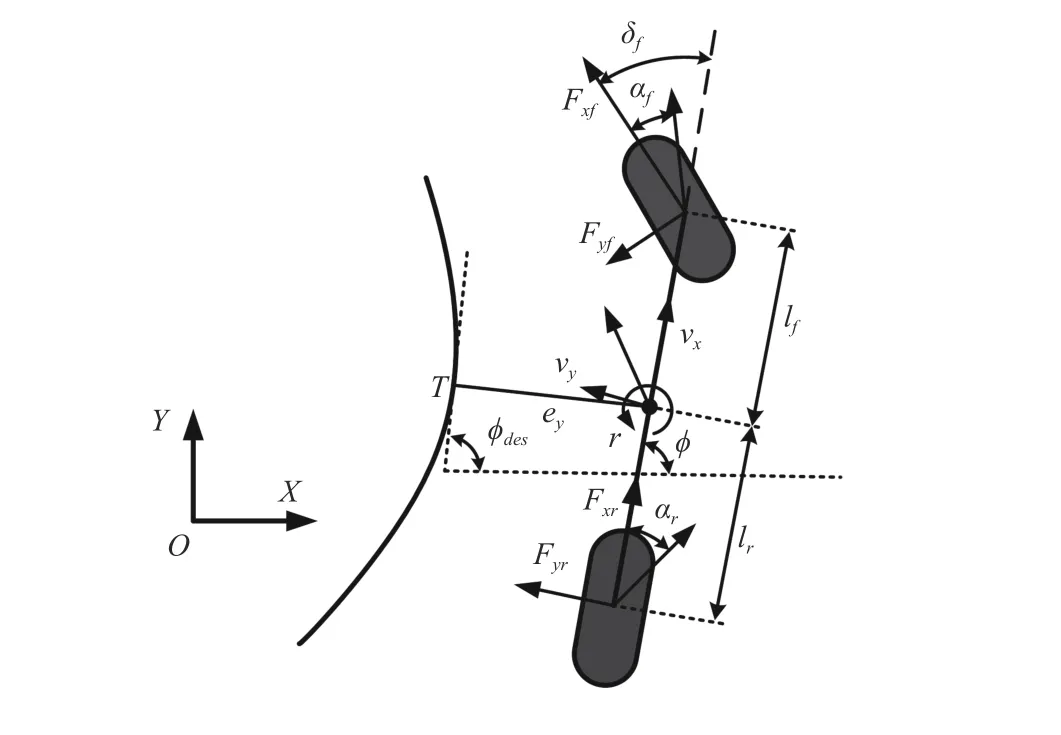
Fig.1.Schematic diagram of the path tracking vehicle model.
In this paper, the AGV dynamic is approximated as a bicycle dynamics model as shown in Fig.1, whereeydenotes the lateral distance from the vehicle center of gravity to the orthogonal projection pointTof the desired path, ?desdenotes the desired vehicle heading angle,?denotes the vehicle heading angel,r= ?˙ denotes yaw rate, and δfdenotes steering angle of the front wheel.vxandvydenote the lateral velocity and longitudinal velocity,FxfandFxrdenote the lateral forces of front and rear wheels,FyfandFyrdenote the longitudinal forces of front and rear wheels, αfand αrdenote the sideslip angles of front and rear wheels, andlfandlrdenote the distances from the vehicle center of gravity to the front and rear axles.The vehicle dynamic model is given by [24]



B.LPV Model With Input Constraints

In addition, consider the effect of actuator saturation, i.e.,

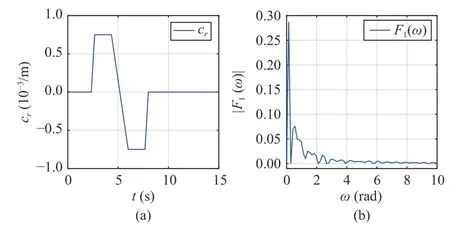
Fig.2.Simulation results for the single-lane change manoeuvre.(a) shows the path curvature for the single-lane manoeuvre; (b) shows the corresponding spectrum map of d2.

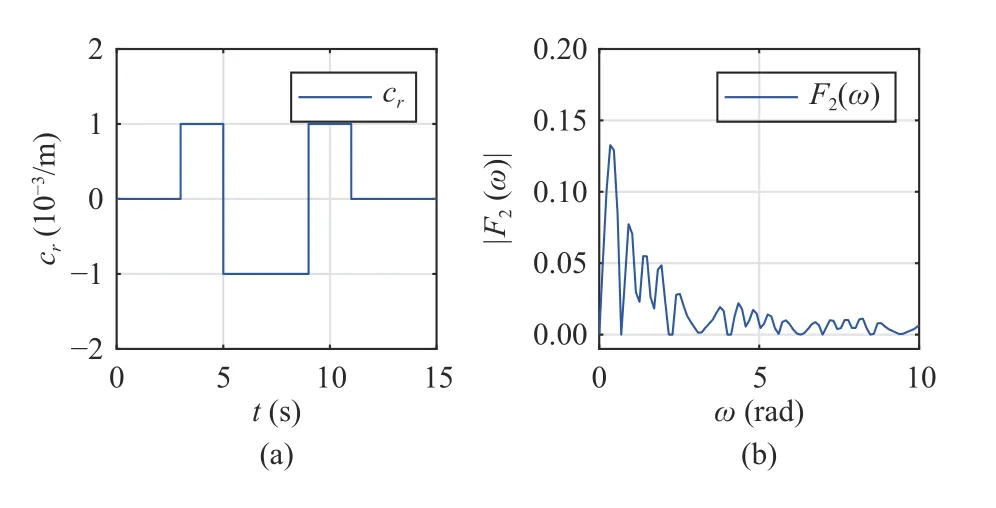
Fig.3.Simulation results for the double-lane change manoeuvre.(a) shows the path curvature for the double-lane change manoeuvre; (b) shows the corresponding spectrum map of d2.

III.PATH TRACKING CONTROLLER DESIGN
For system (10), an observer-based path tracking controller is designed as [1] and [16]







The inequalities provided in Theorem 1, and Corollaries 1?3 are of infinite dimension, which makes it not feasible to calculate the observer gain and the controller gain.These infinite dimensional inequalities are converted into finite LMIs in the following theorem, which can be utilized to calculate the observer gain and the controller gain through the LMI toolbox readily.


IV.NUMERICAL RESULTS

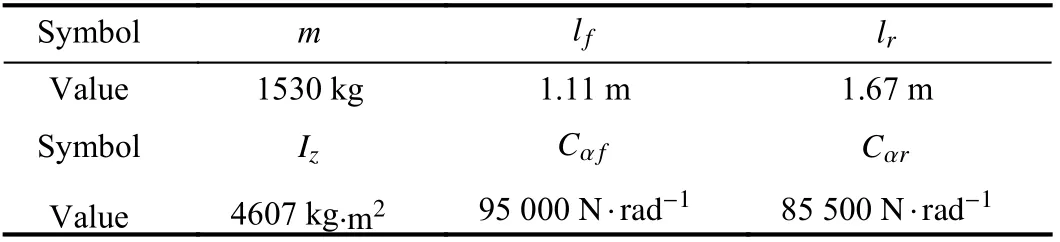
TABLE I MAIN PARAMETERS OF THE VEHICLE

A.Single-Lane Change Manoeuvre
Consider a single-lane change manoeuvre, as shown in Fig.2(a).The responding curves of system states and their estimations are shown in Fig.4, from which it can be seen that both the lateral offseteyand relative yaw anglee?converge to small regions around the origin.
To show the advantages of the proposed control method in attenuating disturbances, we compare it with the existing method proposed in [23].The comparison results are shown in Fig.5, where it can be seen that the finite frequency method proposed in this paper receives better disturbance attenuation performance.
In addition, the control method proposed in this paper and the control method without considering input saturation proposed in [33] are simulated under the same conditions.The comparison results are shown in Fig.6, from which it can be seen that the consideration of input saturation is essential and the control method proposed in this paper can yield better path tracking performance of autonomous vehicles with actuator constraints, and the corresponding control input δfis plotted in Fig.7.The global trajectories are plotted in Fig.8, from which it can be seen that the proposed method yields smaller path tracking errors.

Fig.4.Simulation results for system states in the single-lane change manoeuvre.The red solid curves show the state information of the vehicle,i.e., ey, e˙y, e?, and e˙?, respectively.The cyan dashed lines denote the corresponding state estimations.
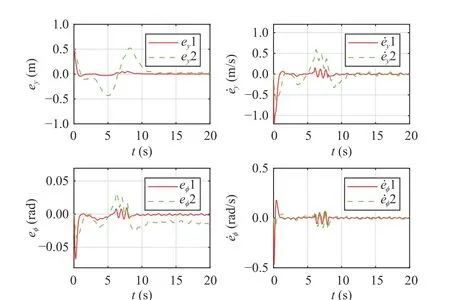
Fig.5.Comparison results for system states in single-lane change manoeuvre.The green dash-dot curves denote the full frequency control method proposed in [23], and the solid red curves denote the control method proposed in this paper.
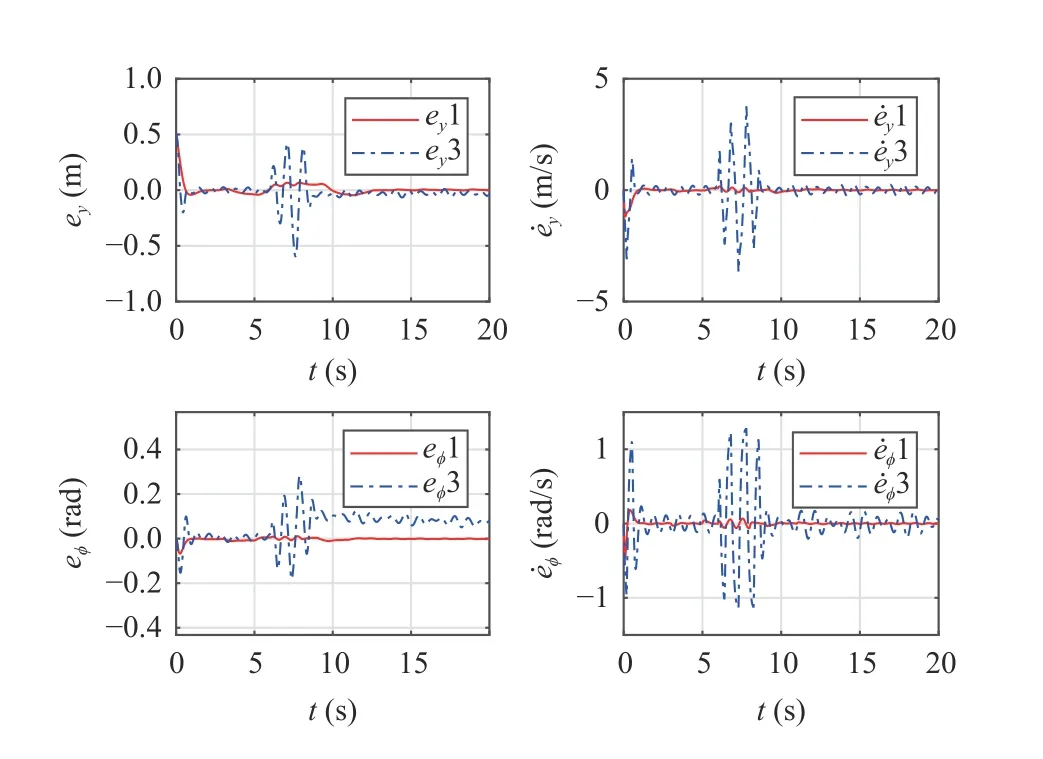
Fig.6.Comparison results of system states in the single-lane change manoeuvre.The blue dash-dot curves denote the control method without considering input saturation proposed in [33], and the solid red curves denote the control method proposed in this paper.
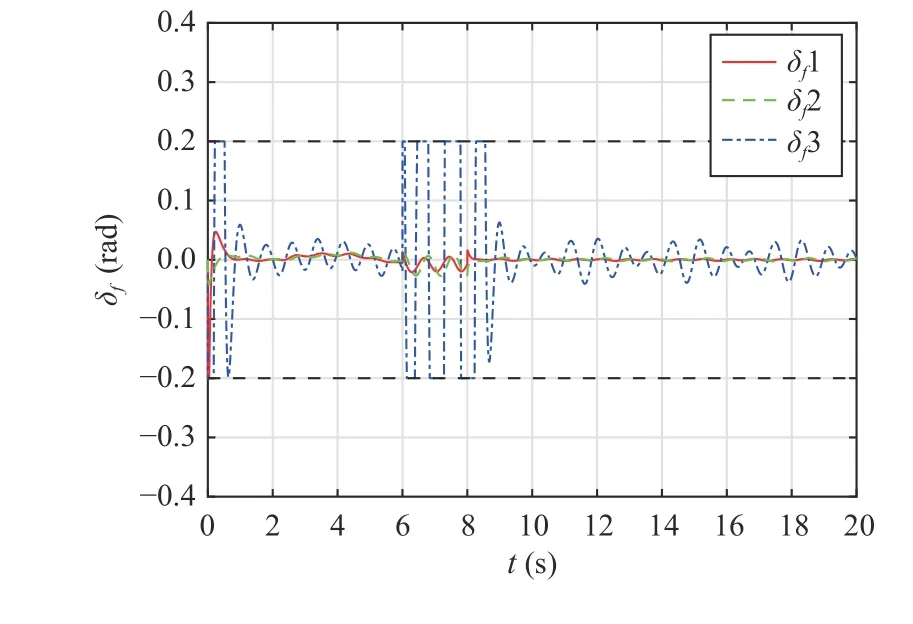
Fig.7.Comparisons results for control input δfin the single-lane change manoeuvre.δf1 denotes the control method proposed in this paper,δf2 denotes the full frequency control method proposed in [23], and δf3 denotes the control method without considering input saturation proposed in [33].
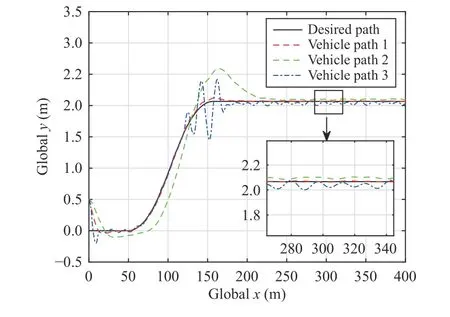
Fig.8.The simulation results for global trajectories in the single-lane change manoeuvre.Vehicle path 1 denotes the control method proposed in this paper, vehicle path 2 denotes the full frequency control method proposed in [23], and vehicle path 3 denotes the control method without input saturation proposed in [33].
B.Double-Lane Change Manoeuvre
Consider a double-lane change manoeuvre, as shown in Fig.3(a).The curves of system states and their estimations are shown in Fig.9, from which it can be seen that both the lateral offseteyand relative yaw anglee?converge to small regions around the origin.
To verify the advantages of the finite frequency method proposed in this paper, the existing full frequency method proposed in [23] and the control method without considering input saturation proposed in [33] are compared under the same conditions.The comparison results of system states are plotted in Figs.10 and 11, and the corresponding control input and global trajectories are plotted in Figs.12 and 13, respectively.All these simulation results verify the effectiveness and advantages of the control method proposed in this paper.
V.CONCLUSIONS
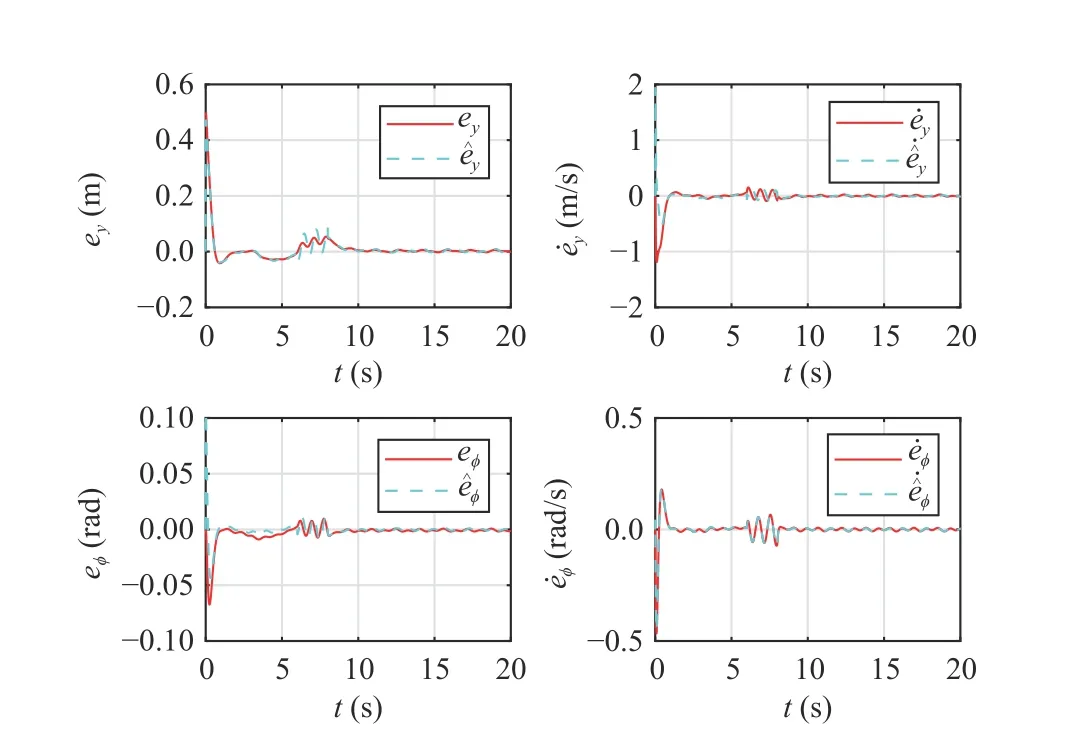
Fig.9.Simulation results for system states in the double-lane change manoeuvre.The red solid curves show the state information of the vehicle,i.e., ey, e˙y, e?, and e˙?, respectively.The cyan dashed lines denote the corresponding state estimations.
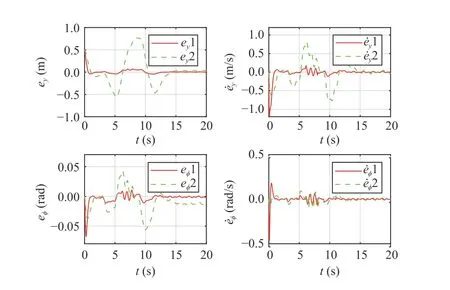
Fig.10.Comparison results for system states in the double-lane change manoeuvre.The green dashed curves denote the full frequency control method proposed in [23], and the solid red curves denote the control method proposed in this paper.
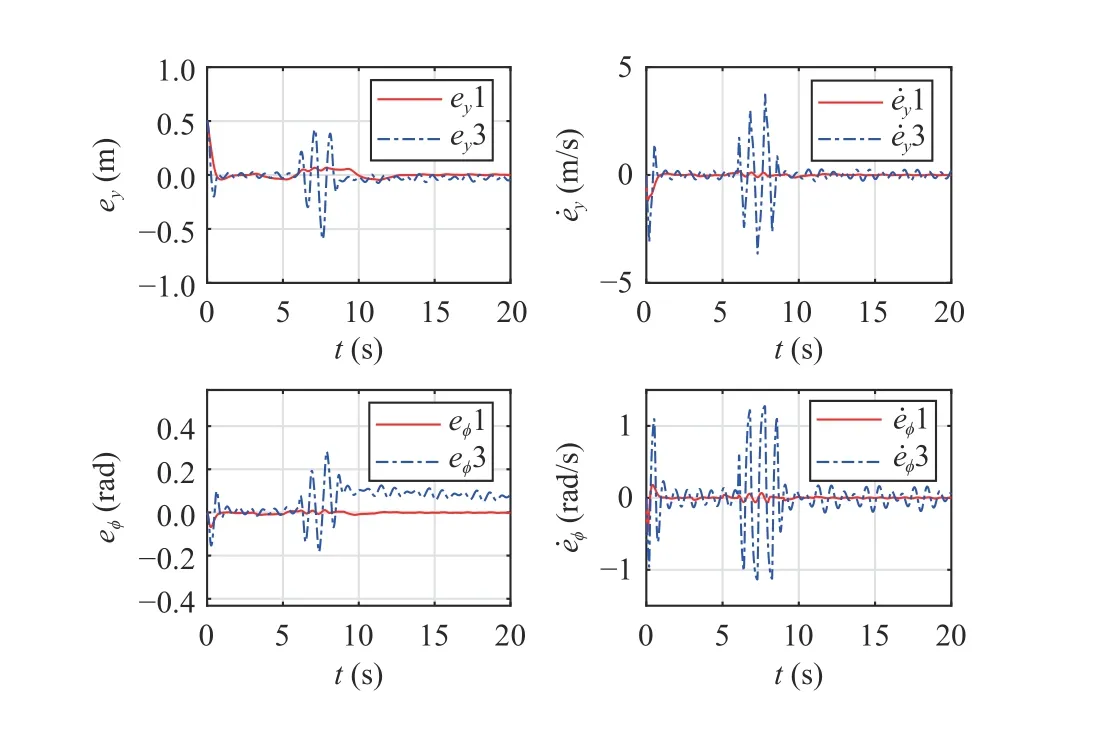
Fig.11.Comparison results for system states in the double-lane change manoeuvre.The blue dash-dot curves denote the control method without input saturation in [33], and the solid red curves denote the control method proposed in this paper.
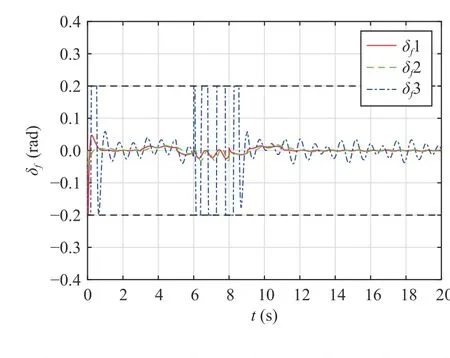
Fig.12.The comparison results for the control input in the double-lane change manoeuvre.δf1 denotes the control method proposed in this paper,δf2 denotes the full frequency control method proposed in [23], andδf3 denotes the control method without input saturation proposed in [33].
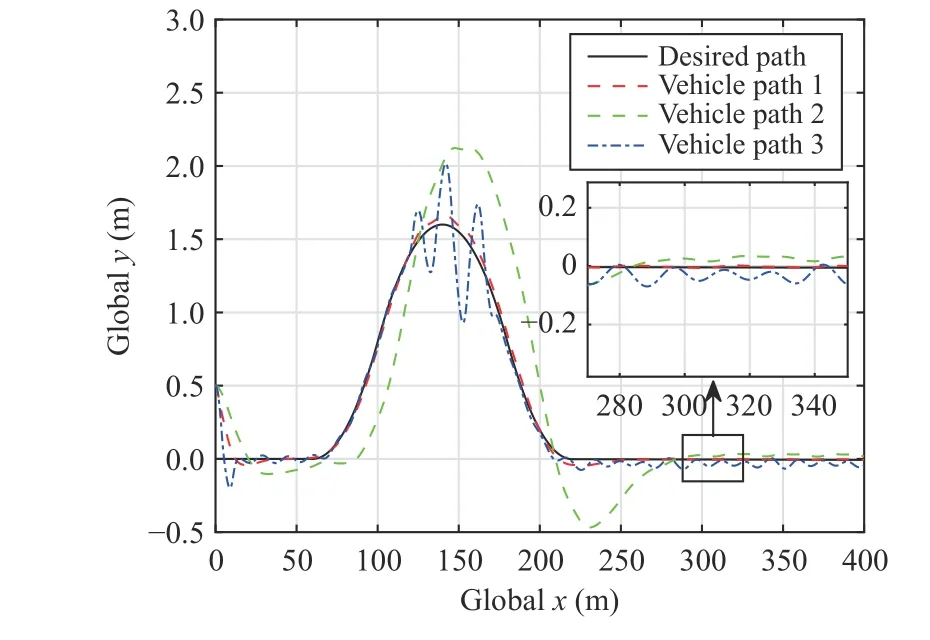
Fig.13.The simulation results for global trajectories in the double-lane change manoeuvre.Vehicle path 1 denotes the control method proposed in this paper, vehicle path 2 denotes the full frequency control method proposed in [23], and vehicle path 3 denotes the control method without input saturation proposed in [33].
This paper investigates the problem of path tracking control for autonomous vehicles with input saturation, parametric nonlinearities and uncertainties.First, an LPV system is constructed by considering the variations of vehicle velocity,which provides a basis for the path tracking of autonomous vehicles.Then, by analyzing the frequency domain characteristics of the derivative of the desired heading angle, a finite frequencyH∞index is proposed to attenuate the effects of the derivative of the desired heading angle on path tracking error,and an observer-based control strategy is designed by taking into account noise effects on the measurement of lateral offset and the finite frequency characteristics of the heading angle.Finally, the effectiveness of the control strategy proposed in this paper is verified under single-lane change manoeuvres and double-lane change manoeuvres.Compared with full-frequency control methods and control methods without considering the input saturation, the control method proposed in this paper achieves better path tracking performance.In the future,the real-time experimental verification of the design method proposed will be explored.
APPENDIX
Lemma 2 [34]:Consider the following system:

 IEEE/CAA Journal of Automatica Sinica2023年3期
IEEE/CAA Journal of Automatica Sinica2023年3期
- IEEE/CAA Journal of Automatica Sinica的其它文章
- Current-Aided Multiple-AUV Cooperative Localization and Target Tracking in Anchor-Free Environments
- Event-Triggered Asymmetric Bipartite Consensus Tracking for Nonlinear Multi-Agent Systems Based on Model-Free Adaptive Control
- UltraStar: A Lightweight Simulator of Ultra-Dense LEO Satellite Constellation Networking for 6G
- Multi-AUV Inspection for Process Monitoring of Underwater Oil Transportation
- Process Monitoring Based on Temporal Feature Agglomeration and Enhancement
- Parallel Learning: Overview and Perspective for Computational Learning Across Syn2Real and Sim2Real
