具有環(huán)境傳播和生理年齡結(jié)構(gòu)的霍亂模型研究
亢躍男, 郭文丹, 聶麟飛
(新疆大學(xué) 數(shù)學(xué)與系統(tǒng)科學(xué)學(xué)院, 新疆 烏魯木齊 830046)
霍亂是一種通過(guò)攝入由霍亂弧菌污染的水或食物引起的急性腸道傳染病.霍亂弧菌可以在環(huán)境中存活1~3周, 甚至更長(zhǎng)時(shí)間, 它主要通過(guò)人與人直接傳播或環(huán)境與人間接傳播.自1817年以來(lái)霍亂發(fā)生了七次世界性大流行, 據(jù)世衛(wèi)組織估計(jì), 每年大約有130萬(wàn)至400萬(wàn)例病例, 以及2.1萬(wàn)至14.3萬(wàn)例死亡[1].時(shí)至今日, 霍亂仍是威脅全球人類生命健康的重大公共衛(wèi)生問(wèn)題.
在過(guò)去幾十年中, 國(guó)內(nèi)外學(xué)者建立了許多具有人與人之間或環(huán)境與人之間傳播的霍亂常微分方程模型[2-5],研究了其無(wú)病平衡態(tài)和地方病平衡態(tài)的存在性與穩(wěn)定性.眾所周知,在生物種群中異質(zhì)性是廣泛存在的,不同年齡段的人接觸疾病的概率是不同的,從而感染疾病的風(fēng)險(xiǎn)也不同,因此,研究具有年齡結(jié)構(gòu)的傳染病模型是很有必要的.為此,一些國(guó)內(nèi)外研究者建立了具有年齡結(jié)構(gòu)的傳染病數(shù)學(xué)模型[6-10],討論了年齡在傳染病傳播中的影響.例如,Lin等[8]提出的類年齡結(jié)構(gòu)霍亂模型中考慮了感染者的感染年齡和環(huán)境中病原體的倉(cāng)室年齡,討論了無(wú)病平衡態(tài)和地方病平衡態(tài)的局部穩(wěn)定性和全局穩(wěn)定性.Yang等[9]建立了偏微分方程和常微分方程耦合的人群具有生理年齡的霍亂環(huán)境傳播模型,給出了疾病的基本再生數(shù),討論了年齡對(duì)霍亂傳播的影響.基于上述討論,本文將建立人群和環(huán)境病毒均有生理年齡的霍亂傳播偏微分方程模型,討論各類平衡態(tài)的存在性和穩(wěn)定性.
1 模型的建立與正解的存在唯一性
將某地區(qū)的人群分為三類: 易感者類,感染者類和恢復(fù)者類,其在t時(shí)刻a年齡的密度分別為S(t,a),I(t,a),R(t,a),記環(huán)境中t時(shí)刻年齡為a的霍亂弧菌濃度為P(t,a).總?cè)丝诘哪挲g密度函數(shù)為N(t,a)=S(t,a)+I(t,a)+R(t,a).根據(jù)病原體在人群和環(huán)境之間的傳播規(guī)律,易感者以λ1(t,a)的速率接觸染病者而被感染,以λ2(t,a)的速率接觸環(huán)境中的病毒而被感染,這里定義如下感染力函數(shù)[11]:
其中:k(a)表示接觸率;β1(a)表示感染者的傳染率;β2(a)表示環(huán)境中病原體的傳染率.進(jìn)一步,令b(a)和μ(a)分別表示單位時(shí)間內(nèi)年齡為a的人均出生率和死亡率,γ(a)和θ(a)分別表示人類年齡依賴的治療率和自然恢復(fù)率,ξ(a)表示感染者的病毒脫落率,δ(a)表示環(huán)境中病原體的自然死亡率.
基于上述假設(shè),建立具有環(huán)境傳播和年齡結(jié)構(gòu)的霍亂模型
(1)
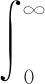
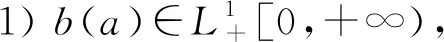
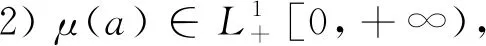
把模型(1)中的前三個(gè)方程相加,得
(2)
模型(2)是標(biāo)準(zhǔn)的Mckendrik-Von Forester方程,沿特征線t-a=c(常數(shù))[12]解得
為保證關(guān)于年齡穩(wěn)態(tài)的存在性,假設(shè)人口的凈再生率等于1,即人口總數(shù)處于平衡狀態(tài),則
從而,模型(2)的穩(wěn)態(tài)解為
初始人口分布滿足:S0(a)≥0,I0(a)≥0,R0(a)≥0,S0(a)+I0(a)+R0(a)=N∞(a),則
對(duì)模型(1)進(jìn)行歸一化處理,令
則
從而,模型(1)可改寫為
(3)
式中:s(t,0)=1,i(t,0)=r(t,0)=p(t,0)=0,t>0.s(0,a)=s0(a),i(0,a)=i0(a),r(0,a)=r0(a),p(0,a)=p0(a),且s(t,a)+i(t,a)+r(t,a)=1.
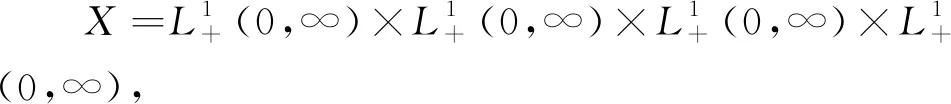

則模型(3)可化為抽象柯西問(wèn)題
(4)
式中:u(t)=(s(t,·),i(t,·),r(t,·),p(t,·))T,u0(a)=(s0(a),i0(a),r0(a),p0(a))T.顯然,當(dāng)t>a時(shí),算子A是C0-半群T(t)的無(wú)窮小生成元,并且算子B在空間X上連續(xù)Frechet可微.定義兩個(gè)集合F={(s,i,r,p)∈X:s≥0,i≥0,r≥0,p≥0}和F0={(s,i,r,p)∈X:0≤s≤1,0≤i≤1,0≤r≤1,0≤p≤K},其中K是正常數(shù).與文獻(xiàn)[13]中引理3.1的證明類似,關(guān)于模型(4)有以下的結(jié)論.
引理1F0是關(guān)于u的正不變集,并且對(duì)于X上的初值u0∈F∩D(A),模型(4)存在唯一的經(jīng)典解.
2 無(wú)病平衡態(tài)的穩(wěn)定性
利用特征方程推導(dǎo)基本再生數(shù)R0的精確表達(dá)式,并證明無(wú)病平衡態(tài)的局部和全局漸近穩(wěn)定性.顯然,模型(3)存在無(wú)病平衡態(tài)E0=(1,0,0,0).令
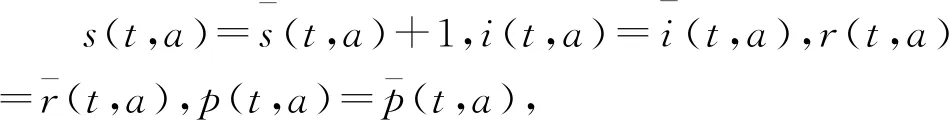
(5)
式中
(6)
式中
(7)
利用常數(shù)變易法求解模型(6)得
(8)
(9)
上式左右兩邊同時(shí)除以V0(V0≠0),得到特征方程
(10)
定義基本再生數(shù)[14]R0:=G(0),即
現(xiàn)討論無(wú)病平衡態(tài)E0的穩(wěn)定性.
定理1若R0<1,則模型(3)的無(wú)病平衡態(tài)E0是局部漸近穩(wěn)定的; 若R0>1,則不穩(wěn)定.
證明由式(10)可知,
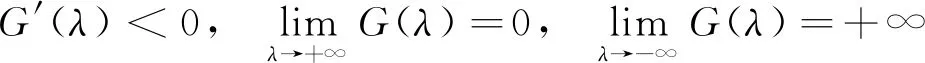
則特征方程(10)存在唯一實(shí)根.如果R0<1,即G(0)<1,那么G(λ)=1存在唯一的負(fù)實(shí)根λ*.進(jìn)一步考慮方程(10)的復(fù)根.設(shè)λ=x+iy是G(λ)=1的任意復(fù)根,則
G(λ*)=1=|G(x+iy)|≤G(x)
由于G(λ)是關(guān)于λ單調(diào)遞減的函數(shù),所以Re(λ)=x≤λ*,即方程(10)的所有復(fù)根都具有負(fù)實(shí)部.因此,當(dāng)R0<1時(shí),模型(3)的無(wú)病平衡態(tài)E0是局部漸近穩(wěn)定的.另一方面,如果R0>1,即G(0)>1,那么方程(10)存在唯一的正實(shí)根,從而無(wú)病平衡態(tài)E0是不穩(wěn)定的.
定理2若R0<1,則模型(3)的無(wú)病平衡態(tài)E0是全局漸近穩(wěn)定的.
證明令f(t,a)=(λ1(t,a)+λ2(t,a))s(t,a),由于s(t,a)≤1,故
f(t,a)≤λ1(t,a)+λ2(t,a)=k(a)V(t)
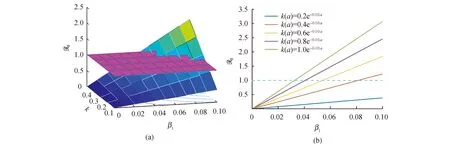
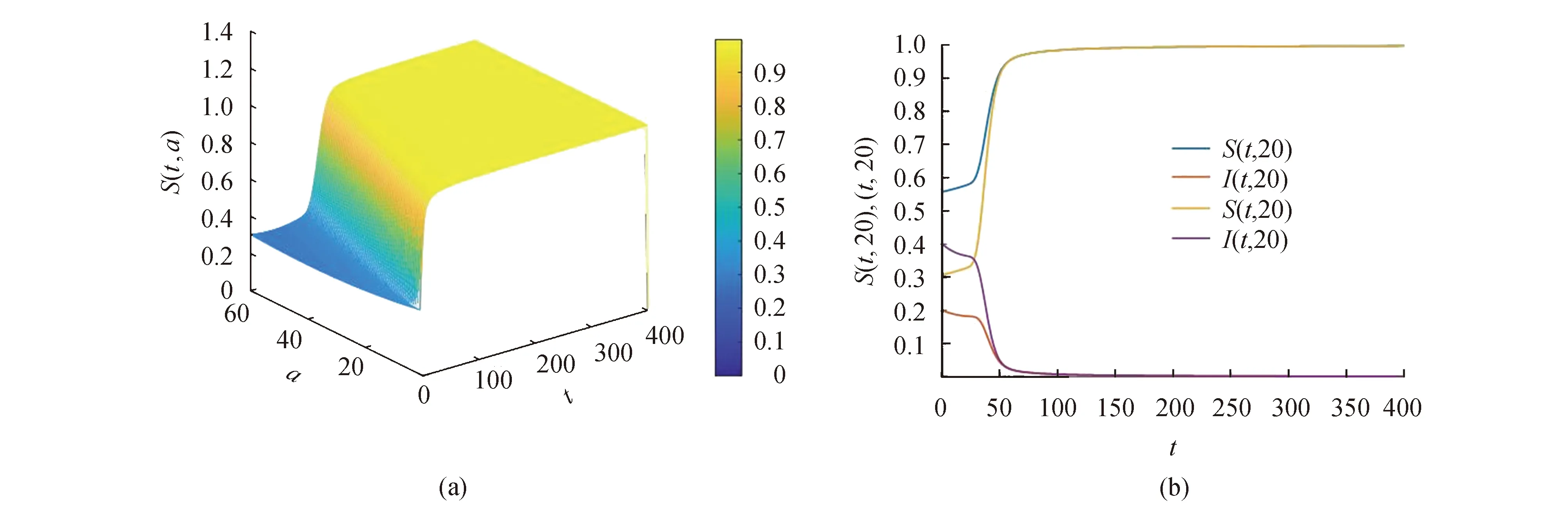
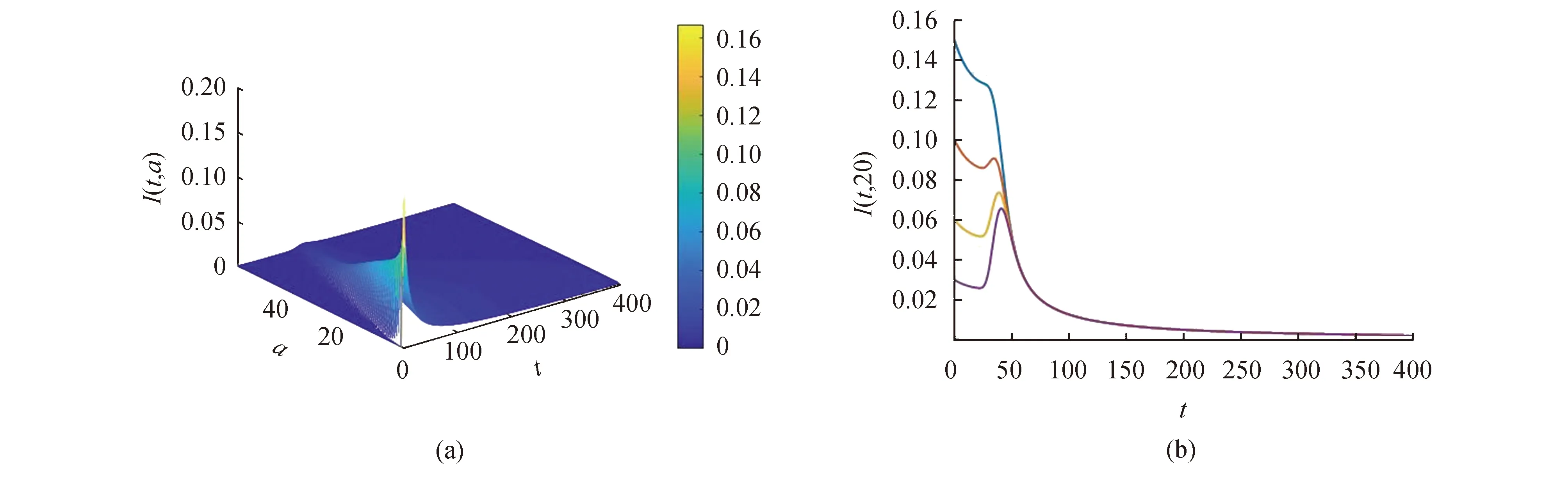
沿著特征線對(duì)模型(3)積分(當(dāng)a (11) 將式(11)中的i(t,a)代入p(t,a)得 (12) 由式(11)中的i(t,a)和式(12)可得 (13) 記常數(shù)M為 則F(a)≤k(a)M.因此, 關(guān)于模型(3)地方病平衡態(tài)的存在性與穩(wěn)定性,有下面的結(jié)論. 定理3當(dāng)R0>1時(shí),模型(3)存在唯一的地方病平衡態(tài)E*(s*(a),i*(a),r*(a),p*(a)). 證明模型(3)的平衡態(tài)必須滿足如下與時(shí)間無(wú)關(guān)的常微分方程組: (14) 式中 (15) 根據(jù)模型(14)可得 (16) 將式(16)中的s*(a)代入i*(a)得 (17) 將式(17)代入式(16)中的p*(a)得 (18) 將式(17)和式(18)代入式(15),并將得到的方程左右兩端同時(shí)除以V*(V*≠0),則 (19) 令V*=0,則 由于s*(a)+i*(a)+r*(a)=1,且s*(a)>0,所以i*(a)<1.又因?yàn)閜*(a) H(β(1+K)N)<1 由于H(V*)是關(guān)于V*單調(diào)遞減的函數(shù),并且當(dāng)R0>1時(shí),有H(0)>1.因此,方程(19)在(0,β(1+K)N)上存在唯一實(shí)根.即,當(dāng)R0>1時(shí),模型(3)存在唯一的地方病平衡態(tài). 討論地方病平衡態(tài)的穩(wěn)定性,將模型(3)在地方病平衡態(tài)E*處線性化,并考慮指數(shù)形式的解 則 (20) 式中 (21) (22) 利用常數(shù)變易法求解模型(21)得 (23) 把式(23)中的y(a)代入u(a)得 (24) 根據(jù)J(ω)的表達(dá)式,把式(23)中的x(a)和y(a)以及式(24)代入式(22)可得 (25) 式中 命題1假設(shè)ψ(a,τ)>0,?0≤τ≤σ≤a,則 1)J(ω)是關(guān)于ω單調(diào)遞減的函數(shù),并且 2)J(0)<1. 證明根據(jù)式(25)和ψ(a,τ)>0可知: J(ω)≥0,J′(ω)<0 在式(25)中,令ω=0,則 (26) 由式(19)可知,式(26)的第一項(xiàng)等于1,所以J(0)<1. 定理4若R0>1,ψ(a,τ)>0,?0≤τ≤σ≤a,則模型(3)的地方病平衡態(tài)是局部漸近穩(wěn)定的. 證明類似于定理1的證明.若R0>1,ψ(a,τ)>0,則J(ω)=1存在唯一的負(fù)實(shí)根,并且所有復(fù)根都具有負(fù)實(shí)部.因此,當(dāng)R0>1時(shí),模型(3)的地方病平衡態(tài)是局部漸近穩(wěn)定的. 迄今為止,已經(jīng)發(fā)展了許多數(shù)值方法來(lái)逼近偏微分方程組的解.利用有限差分法沿特征線離散化模型(1),并進(jìn)行數(shù)值模擬.假設(shè)模型基本參數(shù)如下: γ(a)=0.48sin2(0.1πa) θ(a)=0.26sin2(0.1πa) δ(a)=0.15sin2(0.1πa) ξ(a)=0.5×10-3sin2(0.1πa) 討論模型的主要參數(shù)對(duì)基本再生數(shù)R0的影響,選擇參數(shù)k(a)=0.2e-0.01a,β1(a)=0.000 11e-0.04a,β2(a)=0.075e-0.02a.根據(jù)R0的表達(dá)式,R0與接觸率k(a)和傳染率βj(a) (j=1,2)是正相關(guān)的.這也正如圖1a所示,R0隨著k(a)和β1(a)的增加而增加.此外,圖1b表明,當(dāng)k(a)固定時(shí),可以通過(guò)降低β1(a)來(lái)降低R0.因此,適當(dāng)減少接觸并降低傳染率是控制霍亂傳播的有效措施之一. 圖1 R0關(guān)于k(a)和β1(a)的敏感性 選擇參數(shù)k(a)=0.9e-2a,β1(a)=0.000 11e-2a,β2(a)=0.075e-a,則計(jì)算可知R0≈0.402 1<1.根據(jù)定理2,無(wú)病平衡態(tài)E0是全局漸近穩(wěn)定的.此時(shí),易感者和感染者的密度分布如圖2所示.特別地,當(dāng)a=20時(shí),對(duì)于不同的初值,S(t,20)隨著t趨于無(wú)窮而趨于1,I(t,20)隨著t趨于無(wú)窮而趨于0.這意味著,無(wú)論霍亂暴發(fā)的初始狀態(tài)如何,最終都會(huì)滅絕. 圖2 無(wú)病平衡態(tài)的穩(wěn)定性,R0<1 選擇參數(shù)k(a)=0.9e-a,β1(a)=0.000 11e-0.6a,β2(a)=0.075e-0.4a,則基本再生數(shù)R0≈1.426>1.由定理3可知,模型存在唯一的地方病平衡態(tài)E*.圖3表明,地方病平衡態(tài)E*是局部漸近穩(wěn)定的,當(dāng)a=20時(shí),對(duì)于不同的初值,I(t,20)隨著t趨于無(wú)窮而趨于地方病平衡態(tài).類似的,當(dāng)t趨于無(wú)窮時(shí),S(t,a),R(t,a),P(t,a)的密度分布會(huì)趨于地方病平衡態(tài).這意味著,霍亂將持續(xù)存在. 圖3 地方病平衡態(tài)E*的穩(wěn)定性,R0>1 基于霍亂弧菌傳播方式的多樣性和種群的異質(zhì)性,提出了一類具有生理年齡和環(huán)境傳播的霍亂弧菌在人和人之間,人與環(huán)境之間傳播的動(dòng)力學(xué)模型,這里環(huán)境中霍亂弧菌也引入了年齡結(jié)構(gòu)以刻畫脫落的霍亂弧菌的活性.進(jìn)一步利用半群理論,線性近似,比較原理等方法,獲得了模型全局正解的存在性與唯一性,以及疾病基本再生數(shù)的精確表達(dá)式,證明了當(dāng)基本再生數(shù)小于1時(shí),無(wú)病平衡態(tài)是全局漸近穩(wěn)定的; 而當(dāng)基本再生數(shù)大于1時(shí),無(wú)病平衡態(tài)是不穩(wěn)定的,模型存在唯一的地方病平衡態(tài),并在特定條件下得到其漸近穩(wěn)定性.如何得到不帶附加條件的地方病平衡態(tài)的局部或全局漸近穩(wěn)定性,是進(jìn)一步值得考慮的問(wèn)題.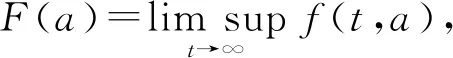
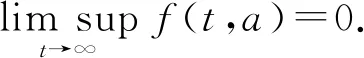
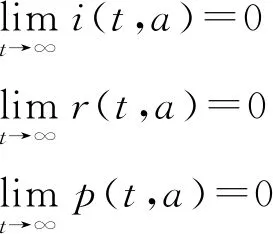
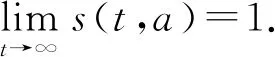
3 地方病平衡態(tài)的存在性與穩(wěn)定性
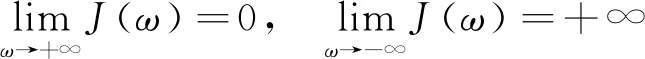
4 數(shù)值模擬
5 結(jié)論

