Dynamics of an SVIR Epidemic Model with Markovian Switching
LI Dan(李丹)WEI Fengying(魏鳳英)
(1.School of Mathematics and Statistics,Fuzhou University,Fuzhou 350108,China;2.Key Laboratory of Operations Research and Control of Universities in Fujian,Fuzhou University,Fuzhou 350108,China)
Abstract: We consider a stochastic SVIR epidemic model with Beddington-DeAngelis infection rate under Markovian switching in this paper.Firstly,we derive the fitness of a unique global positive solution.Then,the sufficient condition Rs0 > 1 for existence of stationary distribution is obtained by constructing the appropriate Lyapunov functions.Moreover,the sufficient conditions including Re0 < 1 for the exponential extinction to the infected individuals are figured out.Consequently,some examples and illustrative simulations are carried out to verify the main theoretical results.
Key words: Epidemic model;Vaccination;Markovian switching;Extinction;Stationary distribution
1.Introduction
In the recent years,many epidemic models were established to study the dynamics of infectious diseases with the bilinear incidence rate in [1-2]and references therein.While,the bilinear incidence rate linearly depended on the number of the infected,which was not consistent with the real situations that the increasing of the number of the infected brought the crowded effect among the infected and also brought the less probability for contacting with the susceptible.So,we governed the Beddington-DeAngelis functional response as a nonlinear incidence rate to describe an SVIR epidemic model in this paper.The Beddington-DeAngelis functional response was firstly introduced by [3-4]and described the mutual interferences between distinct compartments[5].In our SVIR epidemic model,the Beddington-DeAngelis functional response also decreased the mechanisms between the susceptible (or,the vaccinated) and the infected.Precisely,the susceptible (or,the vaccinated) were contacted by the infected accidently with the spreading of infectious diseases,therefore,the susceptible(or,the vaccinated) were quarantined at hotels for a period of time by the local government in China to avoid the contacts with the infected.And,other mechanisms between the susceptible and the infected in epidemic models could be found in [6-8]and references therein.
The epidemic models are inevitably affected by the environmental noises,which usually include the white noises in [9-12]and the telegraph noises in [13-16].The white noises consist of the small fluctuation of continuous sample paths,the effects of the intensities of the white noises to the epidemic models were investigated in [10,12]via replacing the constant parameters by the white noises.The telegraph noises include the transient transitions between two or more sets of parameters in the underlying model that correspond to two or more different environments or regimes.In the most cases,the switching between two or more different environments was usually memoryless,and the switching was modelled with a finite state continuous-time Markov chain with a state space ofM={1,2,···,N},whereNwas the number of different environments.Many authors introduced Markov chains into the epidemic models [13-16]to investigate the dynamics.For instance,LIU et al.[14]introduced the DS-I-A model with the periodic parameter and Markovian switching,and investigated the dynamic behaviors such as the ergodicity and the extinction.LAN et al.[15]proposed and discussed a stochastic SIRS epidemic model with a non-monotone incidence rate under regime-switching.In this paper,we assume that the vaccinated lost their temporary immunities over time and returned to the susceptible again,and propose an SVIR epidemic model with Beddington-DeAngelis functional response under Markovian switching as follows:
whereS(t),I(t),V(t),R(t) are the numbers of the susceptible,the infected,the vaccinated and the recovered at timetrespectively,andAis the constant input rate per unit time,pis the vaccination rate of the susceptible,βandηare respectively the contact rates of the susceptible and the vaccinated with the infected,θis the rate of immunity loss,μis the natural death rate,δis the disease-caused death rate of the infected,τis the recovery rate of the infected,ai(i=1,2,3,4) are the inhibitory effects.Moreover,r=r(t) is a right-continuous Markov chain on the probability space taking values in a finite state spaceM={1,2,···,N}with generatorΓ=(γij)n×ngiven by
Moreover,Bi(t)(i=1,2,3) are three independent standard Brownian motions (or Wiener processes),σi(t)(i=1,2,3) are the intensities of the white noises;(?,F,{Ft}t≥0,P) is a complete probability space with its filtration{Ft}t≥0.DefineRd:xi >0,1≤i ≤d}.For any constant sequence{g(j) :j ∈M},define=minj∈M g(j),=maxj∈M g(j).
We notice that the first three equations of model (1.1) are independent of the recovered,so we consider a stochastic epidemic model (1.2) as follows:
Next,the existence and uniqueness of a global positive solution,and the sufficient conditions for the persistence and the existence of the ergodic stationary distribution to model (1.2)are respectively derived in Section 2.Moreover,the sufficient condition for the extinction of model (1.2) is figured out in Section 3.
2.Fitness and Stationary Distribution
We concern the existence and uniqueness of a global positive solution to model (1.2)before we investigate other long-term properties.Let the solution of model (1.2) beX(t)=(S(t),V(t),I(t)),dB(t)=(dB1(t),dB2(t),dB3(t))T.
Theorem 2.1Model (1.2) admits a unique solutionX(t) for any initial valueX(0),and solution will remain inwith probability one.
ProofWe construct a non-negativeC2-functionW1=S ?1?lnS+V ?1?lnV+I ?1?lnIby the similar approaches in [17-19],then the generalized It?o’s formula implies that
The remaining details are omitted.The proof is complete.
Lemma 2.1[20]The Markov process (X(t),r(t)) to model (1.2) is positive recurrent and ergodic,that is,there exists a unique stationary distributionν(·,·) to model (1.2).If the following conditions are satisfied:
Motivated by the similar arguments in Theorem 3.3 of [19]and Theorem 5.1 of [21],we thus derive the main results of this paper.
Theorem 2.2If1,then the model (1.2) admits a unique stationary distributionν(·),which has the ergodic property,where
ThenU(X,k) is positive definite.Hence
and for allξ ∈D,
whereλmax(U(X,k)) andλmin(U(X,k)) are two continuous functions ofX.Therefore
which implies that
LetW6=M(W2+w(k))+W3+W4+W5,hereMis a sufficiently large constant andmis a sufficiently small constant satisfying
Case 6 WhenX ∈D6,by (2.7),(2.8) and (2.10),we derive
Hence,the condition(H3)of Lemma 2.1 is satisfied.Further,the model(1.2)admits a unique ergodic stationary distributionν(·,·).
3.Extinction
The extinction means the elimination of infectious diseases for a long time.By the similar approaches in Theorem 3.1 of [18],Theorem 3.4 of [19],Theorem 3.1 of [21]and Theorem 3 of [25],the condition for extinction is investigated in Theorem 3.1.
Theorem 3.1If the following condition holds
then,the number of the infected to model (1.2) will exponentially go to extinction.
ProofDefineW7=lnI,applying the generalized It?o’s formula toW7,we obtain
By the ergodic properties ofr(t),we can obtain
So,the number of the infected declines to zero with an exponential rate in a long run.
4.Numerical Simulations
Firstly,we assume that the initial values areS(0)=0.5,V(0)=0.3,I(0)=0.3,and the Markov chainr(t) is on the state spaceM={1,2}with the generator as follows
Obviously,the Markov chainr(t) has a unique stationary distributionπ=(π1,π2)=.
In this section,we take the model (1.2) as an example to perform the numerical simulations.Milstein’s higher order method for stochastic differential equations in [27]was valid for model (1.2),more details are suggested to read [6,18].Other applicable methods for the model (1.2) are referred as [7,28]and references therein.
Example 4.1We choose(I)in Tab.4.1 withσ1=0.5,σ2=0.5,σ3=0.5 fork=1 andσ1=0.3,σ2=0.3,σ3=0.3 fork=2,we thus derive1.0553>1,so the condition of Theorem 2.2 is satisfied.Fig.4.1 shows that the susceptible,the vaccinated and the infected are persistent in the mean for a long run,the corresponding frequencies with probability density functions are demonstrated in Fig.4.2.

Fig.4.1 The persistence in the mean of (S(t),V(t),I(t)) to the model (1.2)
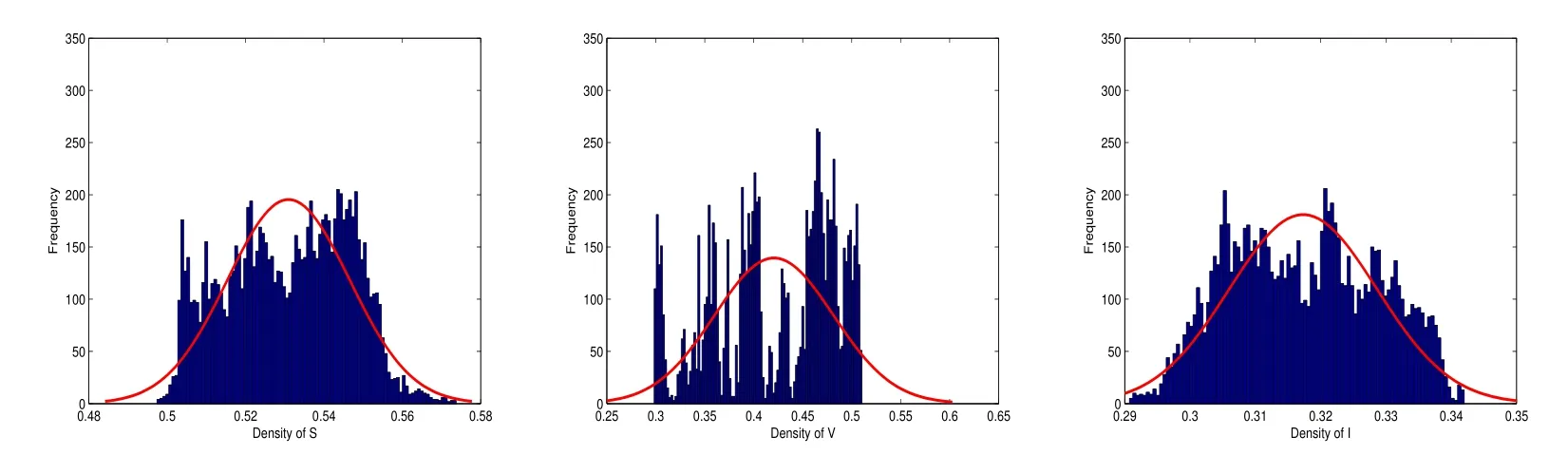
Fig.4.2 The density functions of (S(t),V(t),I(t)) to the model (1.2)
Example 4.2The extinction is discussed by choosing (II) in Tab.4.1 withσ1=σ2=σ3=0.5 fork=1 andσ1=σ2=σ3=0.3 fork=2.It is easy to check that the condition of Theorem 3.1 is satisfied,that is,0.7836<1.Again,we take (II) in Table 1 except forσ2=0.75,we have0.7317<1,so the condition of Theorem 3.1 is valid.The simulations in Fig.4.3 show that the increasing of the intensities for the white noises accelerates the extinction of infectious diseases.
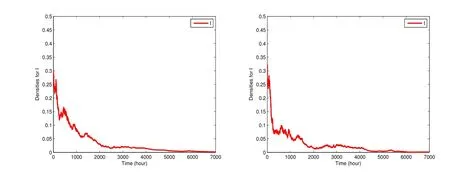
Fig.4.3 The densities of the infected tend to the extinction for a long run as σ2=0.5 and σ2=0.75
- 應(yīng)用數(shù)學(xué)的其它文章
- 粘性Cahn-Hilliard方程的二階凸分裂有限元格式
- A New Adaptive Nonmonotone Newton Algorithm
- Extending Slow Manifold Near an Asymmetric Cusp Point
- The Smoothing Newton Method for NCP with P0-Mapping Based on a New Smoothing Function
- Some Fermat-type Indices of Sierpi′nski Graphs and Sierpi′nski Pyramid
- 求解非線性方程組的修正Fletcher-Reeves共軛梯度法

