Stability of connected and automated vehicles platoon considering communications failures
Run-Kun Liu(劉潤坤), Hai-Yang Yu(于海洋),2,, Yi-Long Ren(任毅龍),2,?, and Zhi-Yong Cui(崔志勇),2
1School of Transportation Science and Engineering,Beijing Key Laboratory for Cooperative Vehicle Infrastructure Systems and Safety Control,Beihang University,Beijing 100191,China
2Beijing Advanced Innovation Center for Big Data and Brain Computing,Beihang University,Beijing 100191,China
Keywords: connected and automated vehicle,car-following model,communication failures,string stability
1.Introduction
The road traffic system is a complex nonlinear physical system, and numerous researchers have focused on how to model vehicle following behavior.Connected and automated vehicles(CAVs)are widely considered to be the future of vehicle development.[1]As the highest level of intelligent vehicles defined by the Society of Automotive Engineers(SAE)International,they are capable of fully autonomously driving based on sensors and communication.[2]They have vehicle-vehicle and vehicle-road communication capabilities, which makes them different from ordinary automated vehicles(AVs).They can obtain information about vehicles farther ahead and therefore achieve closer following and rapidly respond as needed.These characteristics make it possible to significantly improve traffic conditions and reduce energy consumption.[3–8]
Ideal vehicle-to-vehicle(V2V)communication is the basis for ensuring the advantages of CAV platoons in all aspects.However, communication is generally established with dedicated short-range communication (DSRC).[9]Owing to the high mobility of vehicles, this type of connection has a high probability of packet loss or even complete interruption.[10–14]As a result, vehicle–vehicle communication may fail in environments such as tunnels or extreme weather.Malicious network attacks can also cause CAV communication failures.Any of these random circumstances can cause CAVs to lose their functionality.
Once the communication capabilities of one or more vehicles in a platoon are lost,the communication topology of the platoon changes.Most of studies have focused on a certain communication topology to model the CAV following state,but this setup is not easily applied to the communication failure scenario.[15–20]A new carfollowing model that can describe both the normal state of communication and the communication failure state is needed.[12]In particular,the model must have a clear physical meaning.
In addition, the influence of communication failures on stability should be analyzed in detail to identify the optimal CAV control parameters under different communication environments.[21]The results of such a study are needed to design a controller with communication robustness.
Therefore, the goal of this study is to develop a unified model that can describe the following state of each vehicle within a CAV platoon.Such a model can be applied to dynamic communication topologies, especially in a scenario of partial communication failures among the platoon vehicles.Based on this model,string stability analysis can be performed to quantify the influence of communication failures.The contributions of this study are as follows.
(i) We propose a general CAV model based on dynamic communication topologies.A revised intelligent driver model(IDM)can be built and used to describe the vehicle-following states of a platoon for both normal and failed communications.The weights of the information obtained from other vehicles are dynamically updated.The model is called the DC-IDM.
(ii)We analyze the changes in the communication topologies after communication failures in a platoon.The possible types of communication topologies are explored,and their probabilities are analyzed.
(iii) The effects of different communication failure scenarios on the stability of a platoon are analyzed by using theoretical study and numerical experiments.The conditions for the stability of a platoon and the probabilities of critical communication failures are obtained.
The remainder of this paper is organized as follows.In Section 2 previous studies are summarized.In Section 3 a general description of the dynamic communication topology following model is provided and the DC-IDM is presented.In Section 4 a theoretical analysis of the stability of platoons with dynamic communications topologies is conducted.In Section 5, a numerical experiment is performed to analyze the stability variations in different scenarios.In Section 6 some conclusions are drawn from the present study.
2.Literature review
In the field of car following models, numerous models that simulate CAV designs have been developed.Typical models can be classified into two categories,i.e., physical models and control models.First, in the physical models, researchers have transformed human-driven vehicle models into CAV models by adjusting their parameter values and adding new parameters that simulate data from multiple preceding vehicles.[22]For example,several improved models are based on the IDM and optimal velocity (OV) model.[23–29]Second,in the control models, such as various cooperative adaptive cruise control (CACC) models, they have been developed by using control theory.[10,30,31]Yuet al.comprehensively reviewed these models.[1]In this study,we use a physical model for analysis,as it is more generalizable.Based on these models,researchers have concluded that CAVs can effectively improve the efficiency and flow stability of traffic.
Considering the characteristics of CAV platoons, the communication topology, which describes the V2V connection between CAVs in a platoon,is a key element for modeling.Typical communication topologies include predecessor following (PF), leader predecessor following (LPF), and multipredecessor following(MPF).[32]Researchers have conducted CAV-related studies of different communication topologies.For example, in Ref.[33], the PF topology degraded the performance of CAVs after a communications interruption.A different model was used to represent the vehicle-following state after degradation.Halderet al.proposed a control method for which the performance does not degrade when CAVs cannot communicate with preceding vehicles.[11]A general consensus among researchers about which communication topology should be used for CAVs is lacking.However, the inclusion of multiple preceding vehicles is generally assumed to effectively mitigate disturbances in a platoon.Dunnet al.[34]and Davis[35]concluded that communication with multiple preceding vehicles can effectively eliminate platoon perturbations,even with communication delays.Zhenget al.analyzed the influences of different communication topologies on platoon stability.[32]
Platoon stability research has focused on mixed platoons, including human-driven vehicles (HVs), AVs, and CAVs.[36–38]The analyses in such studies are almost always based on a certain communication topology.However, communication failures occurring in a platoon change the communication topology.Liuet al.[39]found that the communication failures in the MPF configuration cause more complex changes in the communication topology.Related studies based on changes in the communication topology have begun and received the attention of researchers.[40]Wanget al.[41]used model prediction control (MPC) to ensure the stability of CAVs subjected to communication topology changes.Zhai and Wu developed a self-delayed feedback controller that determines acceleration values based on the current and historical speed and headway of a vehicle,independent of the reception of information from the vehicle ahead.[42]Liet al.[43]proposed a distributed model predictive control(DMPC)method for multivehicle system control under changes in the communication topology.Sunet al.[21]determined how many vehicles are needed to establish communication connections based on the actual state of communications.Given the limitations of the communication distance among CAVs, Zhouet al.[7]studied the possible degradation of platoons and analyzed variations in the macroscopic traffic flow efficiency.Few studies on stability analysis considering communication failures have transformed the problem into a heterogeneous platoon;[44]in general, communication failures are assumed to lead the degradation to be controlled,and PF is used.
Based on the analysis of previous studies, two problems remain to be solved,i.e.,car-following modeling cannot adapt to dynamic communication topologies, and platoon stability analysis under a communication failure is simplified into heterogeneous traffic flow analysis.The few studies that have addressed platoon communication topology change scenarios have mostly adopted a control point of view.[16]
Therefore, in this study, a unified dynamic communication topology-based car-following model is built, which can describe the following state of all vehicles after communication failures occur.Stability analysis is conducted based on the unified model to reveal the influence of communication failures on the platoon.
3.Model
The functionality of CAVs is based on V2V communication.Vehicle driving decisions are made by information about which vehicles and how many vehicles are ahead.This information is supported by the communication topology of the platoon.In this section, a general car-following model based on dynamic communication topologies is established.The model is called the DC-IDM.
3.1.Communication topology
The different communication topologies within a platoon directly determine the information applicable to a vehicle for driving decisions.The topology form is generally limited by the communication protocol between vehicles, the wireless communication distance,and other conditions.Topologies include PF,LPF,and MPF as shown in Fig.1.
As shown in Fig.1,a CAV can at least obtain information about the vehicle immediately ahead of it by detecting the vehicle or by receiving information from the vehicle.However,the only way to obtain the driving status of vehicles farther ahead is through wireless communication.The vehicle information is a function of the current communication topology.For example, CAVs can obtain driving information from the lead vehicle of a platoon, as shown in Fig.1(b).If the communication topology is shown in Fig.1(c), the driving state of multiple vehicles ahead can be obtained.Once the communication capability of one vehicle in the platoon fails, the communication connection associated with it is lost, and the communication topology of the platoon changes.For example, in Fig.1(c), when the communication of vehiclen+1 fails,the control mode degenerates from CACC to ACC.The communication topology of the platoon then changes into that shown in Fig.1(d).In this case,vehiclen+3 will not receive the information from vehiclen+1, andn+2 will only sense the driving status of the vehicle ahead of it through its own detectors.However,vehiclesn+2 andn+3 are not degraded.Notably,the influences of a communication failure under different topologies are different.
In previous studies, different communication topologies have been used to build their corresponding models and analyze the platoon stability.In these studies, a certain topology was assumed for the vehicles in the platoon.However, there is still no consensus about which topology CAVs should be adopted.The topology is dynamic and based on actual communication conditions,so different topology forms should be used to form platoons.Even if a single communication topology is assumed for a platoon, its form can be changed when communication fails(e.g.from Fig.1(c)to Fig.1(d)).Therefore,a CAV-following model must take the dynamic communication topologies into consideration.

Fig.1.Communication topologies in a platoon.
3.2.The dynamic communication topology-based carfollowing model
A car-following model is generally a continuous acceleration equation, the solution of which is determined by the speed and spacing of a vehicle relative to the vehicle ahead of it.[45–47]The generalized form is as follows:
where ˙vn(t)represents the acceleration of vehiclenat timet,f1(·)is a nonlinear function,sn(t)=xn?1(t)?xn(t)?lrepresents the gap between vehiclenandn?1,xn(t)is the position ofnat timet,lis the vehicle length,vn(t) is the speed of vehiclen,?vn(t)=vn?1(t)?vn(t)is the difference in speed between vehiclenandn ?1, andτis the response delay of vehicle;[21,46]in general,to simplify the model,τcan be taken as 0,which means no delay in communication.This model is only applicable to the PF topology.
The CAVs can obtain information from multiple vehicles ahead,so the acceleration expression in Eq.(1)can be rewritten as
The existing models assign a value to each weight.As shown in Fig.1(c),vehiclen+2 obtains information from vehiclen+1 and vehiclen;Wanget al.[12]assumed thatw1=0.8 andw2=0.2.When the communication of carn+1 fails,n+2 can only obtain the driving status ofn+1 through detectors,and the information about vehiclenis lost(Fig.1(d)).In this scenario,the weights should be updated tow1=1 andw2=0.A failure to update the weights in real time according to the changes in the communication topology leads to abnormal acceleration.
To make a car-following model adapt to change in its communication topology, we first model the communication topology of a platoon.The topology is represented as a directed graphG=(V,E), whereVis the set of nodes, andEis the set of edges.We define each vehicle in the platoon as a node,V=1,2,...,n.E ?V×V={e1,1,e2,1,...,ei,j}represents the edge where all communication connections are established in the platoon, withiandjbeing inV.An edgeei,j=1 means that vehicleican receive information fromj;otherwise,ei,j=0.The adjacent matrix of graphGcan be expressed asA(G)given below:
whereci,j=ei,j.
Taking Fig.1(c) for example, the communication topology can be represented by the following matrix:
When the communication of vehiclen+1 fails, the matrix changes into
We need a method of updating the weights assigned to the obtained information according to changes in the communication topology.The method must satisfy two properties,i.e.,[39](i)the farther ahead the vehicle sending a message is,the smaller the weight assigned to the message is.(ii)When a vehicle cannot send information, its message weight is 0.The weight of the remaining vehicle information is increased, but the more distant the vehicle is,the smaller the weight increase is.
A power function can satisfy the above requirements,such as Eq.(6), whereμis a constant greater than 1.If vehiclenhas received the information sent byMvehicles ahead,thencn=[0,...,cn,n?M,...,cn,n?1,0,...,0], wherecn,n?M=cn,n?1=1.We definewn,n?mas the weight to which vehiclenassigns the information from them-th vehicle ahead.Then,wn,n?mcan be expressed as Eq.(7).
For a platoon of 8 vehicles withM= 5, the communication topology of the 7th vehicle can be written as the vectorc7=[0, 1, 1, 1, 1, 1, 0, 0].Whenμ=2,we can obtain the weight coefficients as indicated in Eq.(8).Equation(7)shows that the coefficients satisfy property 1:wn,n?1>wn,n?2>···>wn,n?M,and.If the communication of the 5th vehicle fails,the communication topology vector changes intoα7=[0, 1, 1, 0, 1, 1, 0, 0].New weight coefficients can be calculated from Eq.(9).Thewn,n?3becomes 0,andwn,n?2increases more thanwn,n?5.Property 2 is also satisfied.A larger value ofμmeans that the information from the closer vehicles has a higher weight.
wn,n?1=0.52,wn,n?2=0.26,wn,n?3=0.13,
Therefore, the generalized form of the dynamic communication topology-based car-following model can be expressed as
Here,f2(·)is a function ofcn,n?mandμ.
3.3.Communication topology
In this subsection, a dynamic communication topology model is proposed for simulation analysis.We modify the intelligent driver model (IDM) proposed in Ref.[29].The IDM is chosen for three reasons.First,the IDM assumes that each vehicle has its desired time headway,which is consistent with the driving characteristics of AVs.Second, the acceleration equation of the IDM is continuously differentiable with respect to all three variables, which is necessary for stability analysis.Third,the IDM has been applied to many CAV studies.
wheres?is the desired distance between vehicles,sis the actual distance between vehicles,tdis the desired time headway,amaxis the maximum acceleration, anddis the comfortable deceleration.In the model,when the actual distance between vehicles is large, the vehicle gradually reduces the distance with a smooth acceleration.When the vehicle is driving too fast or is too close to the vehicle in front of it,the vehicle slows down until it reaches the required spacing.All these features can be better adapted to the driving characteristics of AVs,so the model is widely used in AV-related research.[5,12,21,23,25]After communication failures occur,the control model degenerates to ACC,and the IDM is a good option.
The classic IDM only considers information about the nearest preceding vehicle.The revised IDM shown in Eq.(12),which is called the DC-IDM, is based on the ability of a CAV to obtain information from multiple vehicles and dynamic communication topologies.The model can make driving decisions based on the actual communication topology at timet.The information obtained from multiple preceding vehicles is weighted according to the communication topology.IfM=1, then the model degenerates to the classic IDM.If the communication topology does not change, the model is a CIDM[12]or an MAC-IDM.[21]
4.Stability analysis
4.1.Definition of platoon stability
If a platoon is stable,when a vehicle in the platoon,which is in equilibrium,causes a disturbance,the response of the vehicles to the rear of the disturbance is not constantly amplified.Each vehicle maintains the same spacingseand speedve=V(se)without acceleration or deceleration, which is defined as the equilibrium state.The model can be expressed asf(seve)=0 when it is in the equilibrium state.
According to the root formula,λ+andλ?are a pair of complex solutions of Eq.(17).If the real part ofλ+is less than or equal to zero at anyθ, the platoon may be stable, and for the opposite condition, it may be unstable.[21,28]The geometry ofλ+atθ=0 determines the stability type.λ+is expanded intoλ+=λ1iθ+λ2(iθ)2+···aroundθ →0 whereλ1andλ2are real coefficients.The e?iθis expanded into e?iθ= 1?iθ+(iθ)2/2+···.Substitution of he two expanded equations into Eq.(17)yields
Here,λ1andλ2can be found to be
Thus, the platoon is string stable ifλ2≤0.Becausefs>0,fv<0,the stability condition is
4.2.Stability of dynamic communication topology-based car-following model
When the communication topology of a platoon is not changed, the proposed dynamic communication topologybased car-following model degenerates into the CIDM described in Ref.[12].Then, equation (14) can be rewritten as Eq.(21),the corresponding Eq.(15)can be written as Eq.(22),and equation(17)can be written as Eq.(23).
The solution to Eq.(23)can be found to be
Therefore, the stability condition for an unchanged topology is represented by inequality (25).The stability of a platoon is related to the weights of the information obtained about the vehicles ahead.
4.3.Probabilistic model of communication topology in a platoon
When the communication of some vehicles in a platoon fails, the weights assigned to the information obtained by the rear vehicles according to Eq.(7) change, which changes the stability of the platoon.However,different types and numbers of failures bring different changes to the weights.Therefore,modeling the failure probabilities of different communication topology forms is important.

Table 1.Probabilities of different communication topologies for M=3.
We start with an infinitely long platoon in which each vehicle can obtain driving information fromMvehicles ahead,and the probability of a communication failure for each vehicle isp.Then, whenM=3, the communication topology form of vehiclejwill be one of 9 cases, each with the probability shown in Table 1.These 9 cases can be divided into 4 categories, each of which represents the information that is essentially available to vehiclen.For example,in categoryA,vehiclencan obtain the information about all 3 vehicles ahead of it, and in categoryC, vehiclencannot obtain the information about only vehiclen?3.
According to Table 1,scenarios 1–3 indicate that the communication of only one vehicle in front of vehiclenfails,which results incategories of communication topologies.Scenarios 4–6 indicate two vehicle communication failures,so?(?1) categories of new topologies appear because?1 categories are duplicates.Similarly, we can obtain the new categories for each additional vehicle communication failure.All communication failures of a front vehicle belong to the same category as the communication failures of vehiclejitself.The communications of all vehicles are normal,and only one failure can be considered to be in the same category.Thus, for the scenario in which a vehicle can obtain information aboutMpreceding vehicles,several categories of topologies may arise as follows:
The probability expressions for each category are shown in Table 2.

Table 2.Probabilities for each category of communication topology.
4.4.Stability analysis after a communication failure
Reference[54]presented the stability conditions for platoons containing different types of vehicles, such as cars and trucks.The results have been widely used for heterogeneous traffic flow stability analysis.[50,51,55]In this study,when some vehicles lose their communication functionalities in a platoon,the CAVs change their communication topologies.Vehicles that make driving decisions based on different types of information can be considered to be in different vehicle categories.The percentage of vehicles in each category can be calculated from Table 2.Their stabilities can be obtained according to Eq.(25) and given in inequality (27), by considering a dynamic communication topology.WhenM=1, the stability condition degenerates to the results presented in Ref.[54].
To consider the possibility of a communication failure,the vehicles in a platoon are divided intoKcategories based on their communication topologies.The inequality(27)can be rewritten as follows:
wherePkandwkare the probability of occurrence of thek-th category of communication topology and the weighting factor,respectively.The weighting factor is expressed as follows:
which is associated with Eq.(7).We can easily find that the stability condition is related to the proportion of different types of topologies and the weighting factor of each type of topology, but unrelated to the location of the vehicle with failed communication.

5.Simulation
In this section,a series of simulations is performed to analyze the stability of a platoon based on the DC-IDM.The Taylor expansion coefficients,,andof the DC-IDM are expressed as
These coefficients are the functions of the vehicle speed and spacing at equilibrium.In this state, all vehicles run at speedveand have a stable spacingse.The relationship betweenveandseis given by
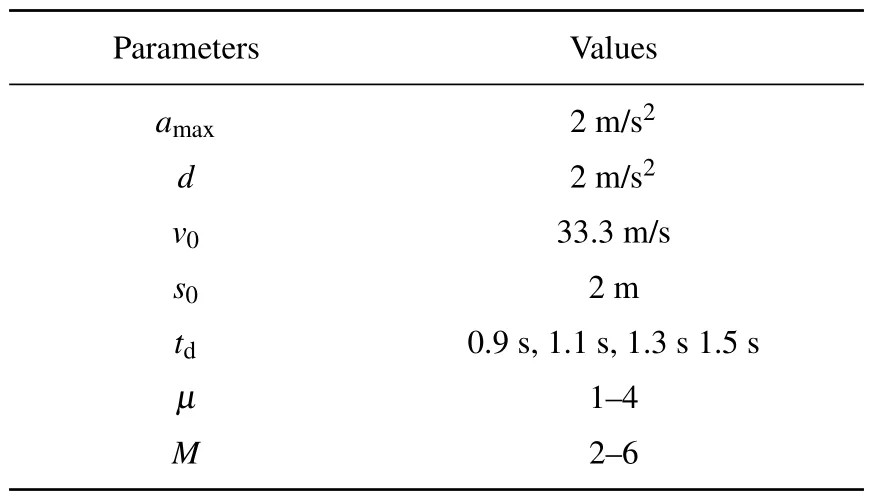
Table 3.Parameters of DC-IDM.
We assume that an infinitely long platoon drives at equilibrium.We simulate the stability at each speed.A communication failure occurs randomly in the platoon.Once the communication failure occurs, the communication is not recovered.The communication failure rate isp, and its value range is 0–1.The parameters of the model are shown in Table 3.
5.1.Platoon stability for normal communication
Our proposed dynamic communication topology model adds two parameters to the classic IDM model,i.e., the parameterMand the parameterμ.We analyze the influences of these two parameters on the stability in a scenario in which CAV communications are normal.
The left-hand part of inequality (25) is the stability discriminant value.Values greater than 0 are for stable status,and values less than 0 are unstable status.The simulation results for different values ofMare shown in Fig.2.At any value of the time headway,the larger the value ofMis,the more stable the latoon is over a wider speed range, which means that the more information the CAV obtains about the vehicle driving ahead,the more stable the platoon becomes.However,CAVs can only obtain information from a few preceding vehicles due to the limited communication distance.The parameter setting of the desired time headway has a significant influence on the stability.
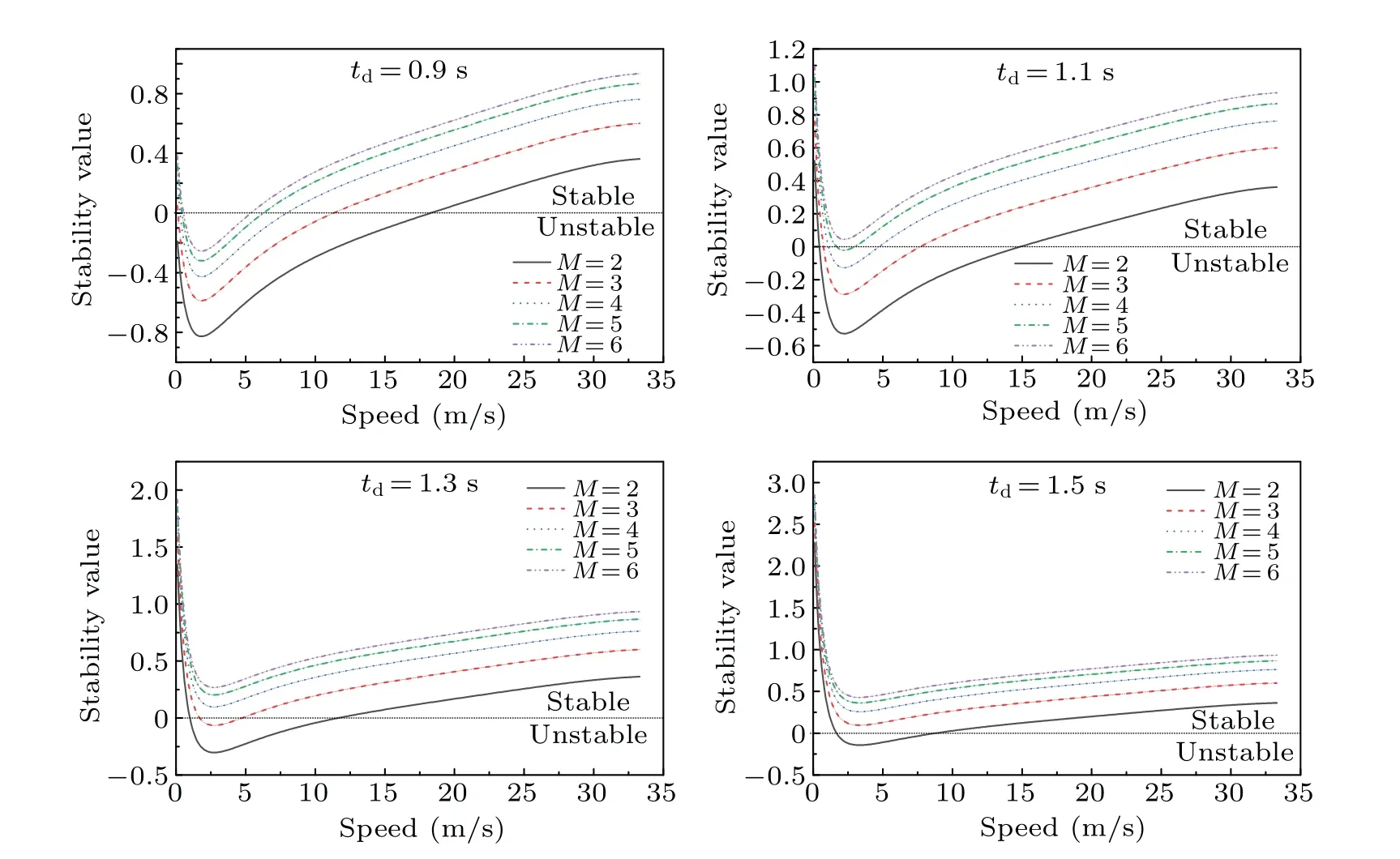
Fig.2.Influence of parameter M on stability(μ =2).
If the expected headway of a CAV is larger,less information is needed to keep the platoon stable.For example, when the desired time headway is 1.1 s, the vehicle needs to obtain information from at least 6 vehicles in front of it for the platoon to keep stable at any speed.For a 1.3-s headway, information is needed from at least 4 vehicles.At 1.5 s,less information is needed,and 3 vehicles are sufficient.This means that setting a more highly desired time headway for CAVs can save communication resources and keep the platoon stable.
Then, takingtd=1.1 s andM=4, we analyze the effect of the parameterμon the stability(Fig.3).A larger value ofμindicates that a vehicle with a greater communication distance sends a lower weight of information.The results demonstrate that a smaller value ofμleads to more stability for the same amount of information from the forward vehicles.For example,the instability speed range is 0.5 m/s–10.8 m/s whenμ= 3.Accordingly, the stability speed ranges are 0 m/s–0.5 m/s and 0 m/s–above 10.8 m/s.Whenμ=2, the instability speed range is only 1 m/s–4.8 m/s, and the remainder of the speed range keeps the platoon stable.The smaller the value ofμis,the more stable the platoon is.We can conclude that the platoon will be more stable when the information sent from vehicles farther ahead of it has a higher weight.When the weight values of the messages sent by each vehicle reach the same value(μ=1),the platoon will be stable at any speed.
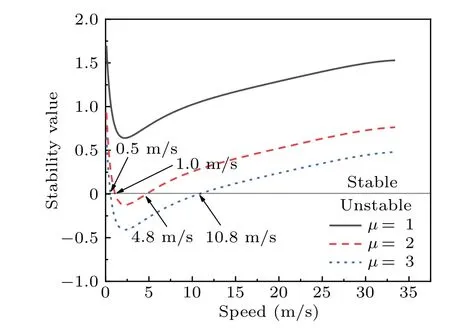
Fig.3.Stability curves for different values ofμ (td=1.1 s,M=4).
5.2.Platoon stability after communication failures
Our model is characterized by its ability to describe the topological changes in the platoon when the communication of CAVs fails.In this subsection, we discuss the stability of a platoon after some of the CAVs lose their communication ability.The left part of inequality (28) describes the platoon stability discriminant value in the case of a communication failure.
First,we analyze the effect of the probability of a communication failure on the stability of the platoon.The results are shown in Fig.4,indicating that the stability decreases continuously as the probability of a communication failure increases.The platoon is stable when no communication failures occur.Once a failure probability is reached, the platoon is unstable in a particular speed range.When all vehicles in the platoon lose their communication ability,they degrade into IDMbased follow-vehicles, which are unstable over a wide range of speeds.
Fig.4.Stability curves for different communication failure rates(td =1.3 s,M=4,μ =2).
To extend the above discussion,we analyze the influences of the probability of CAV communication failures on the stability of the platoon for different communication topologies.As shown in Fig.5, the platoon is not stable in a particular speed range forM=3 regardless of the presence of communication failures.WhenM=4,the minimum failure rate is 8%,which allows the platoon to remain stable at any speed.We define this rate as the critical CAV communication failure rate for platoon stability, below which the platoon is stable.Similarly, we find a critical rate of 15% forM=5 and 19% forM=6.In summary,when a CAV has access to more information about the vehicles ahead of it, the platoon is more likely to remain stable,even under a communication failure.
Additionally, when the speed of a platoon is higher or lower than the speed corresponding to a critical failure rate and if more vehicles lose communications,the platoon can remain stable even if the failure rate exceeds the critical rate.These speed ranges are recommended for the platoon.
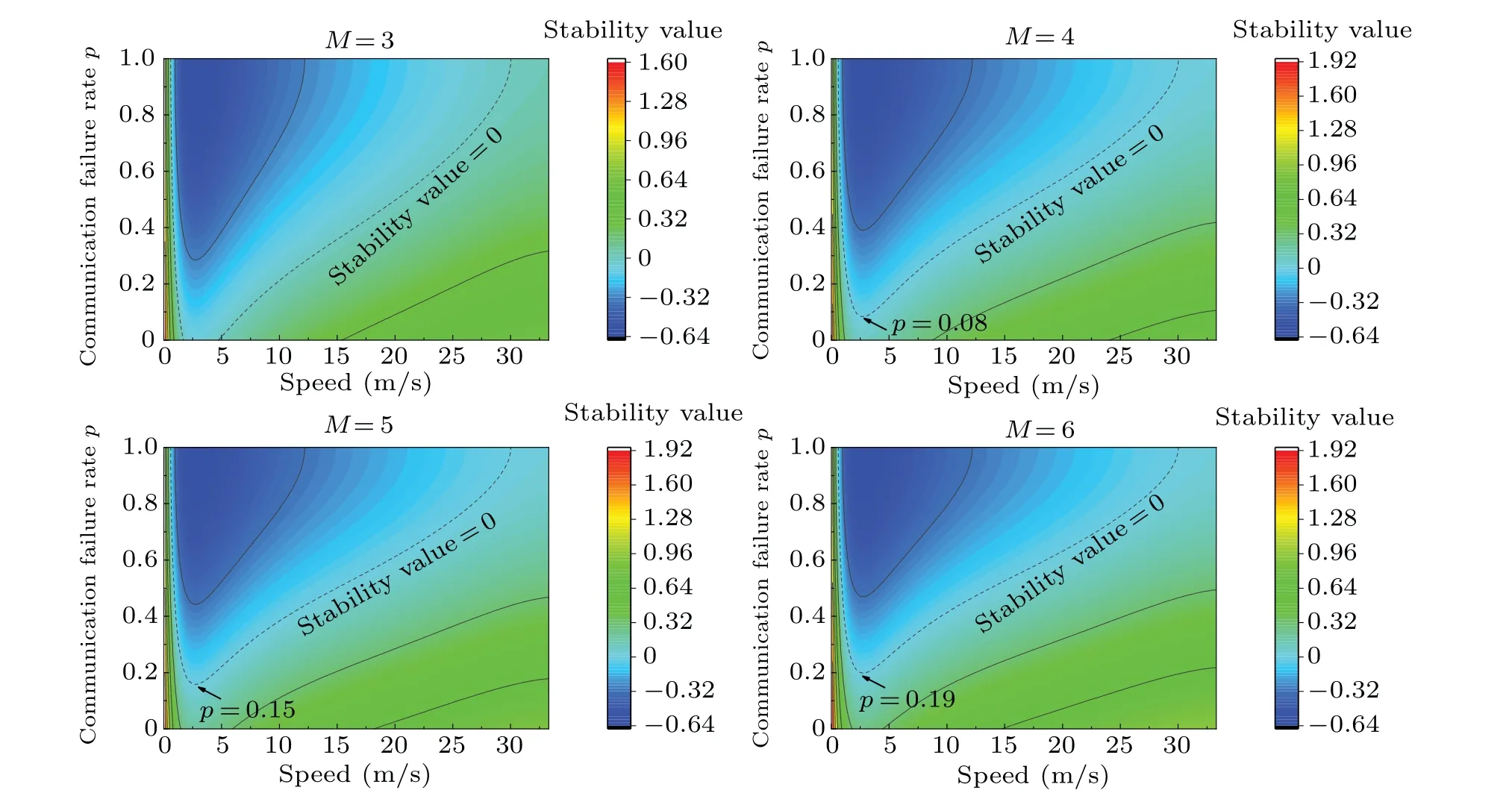
Fig.5.Analytical results of stability for different communication failure rates(td=1.3 s,μ =2).

Fig.7.Analytical results of stability for different communication failure rates(M=4,μ =2).
Based on the DC-IDM,the value ofμcan affect the distribution of the information weights.Assume thattd=1.3 s andM=3.We analyze the influence ofμon the critical failure rate, and the simulation results are shown in Fig.6, indicating that whenμ=1, the critical communication failure rate is 25%.Whenμ=2,there is no critical communication failure rate because even if the vehicle does not have a communication failure, it will not keep stable in the speed range of 1.8 m/s–4.7 m/s.Whenμfurther increases to 3 and 4,the speed range expands to 1.1 m/s–9.7 m/s and 1.0 m/s–13.6 m/s,respectively.The results indicate that if there occurs a communication failure, a smallerμis a good choice for maintaining string stability.
Furthermore, takingμ=2 andM=4 for example, we analyze the effects of different desired headways on the platoon stability in a communication failure scenario.Figure 7 shows that attd=0.9 s andtd=1.1 s,the platoon is not stable in some speed ranges even it there occur no communication failures.Whentdincreases to 1.3 s, the platoon remains stable if the communication failure rate is less than 8%, and the critical failure rate increases to 22%whentdincreases to 1.5 s.The combined results show that the longer the desired time headway is,the larger the critical failure rate is.
6.Conclusions
In this work,the possible effects of CAV communication failures on the platoon stability are analyzed.A car-following model with considering the dynamic communication topologies of CAVs is developed, and a general expression of the model is presented.The model can dynamically adjust the weights of the obtained information based on the actual communication topology after a communication failure has occurred.The IDM model is modified to adapt to dynamic communications.
The communication topologies that emerge after a communication failure are modeled and analyzed with probabilities for each communication topology form.Finally, based on the DC-IDM,the stability of the platoon is analyzed theoretically.The stability conditions for a communication failure are obtained.The numerically experimental results are shown below.
(i) As the communication failure rate increases, the platoon becomes unstable.
(ii)The critical failure rates for different CAV parameter settings are obtained.For example, when CAVs can obtain the information about 4 vehicles driving and the desired time headway is 1.3 s,the critical failure rate is 8%.
(iii) The critical failure rate is improved when CAVs receive information from more preceding vehicles or a larger desired time headway is used.
The results in this study indicate that when CAVs are set with reasonable driving parameters, the stability of a platoon can be ensured even if some of the vehicles lose their communication ability.However, setting a larger desired time headway means less road capacity, and receiving more vehicle information means that more communication resources are needed.Balancing the traffic flow efficiency, communication resources,and platoon stability by optimizing the CAV parameters is the next subject in our research.
Acknowledgements
Project supported by the National Key Research and Development Project of China (Grant No.2018YFE0204300),the Beijing Municipal Science & Technology Commission(Grant No.Z211100004221008), and the National Natural Science Foundation of China(Grant No.U1964206).
- Chinese Physics B的其它文章
- First-principles calculations of high pressure and temperature properties of Fe7C3
- Monte Carlo calculation of the exposure of Chinese female astronauts to earth’s trapped radiation on board the Chinese Space Station
- Optimization of communication topology for persistent formation in case of communication faults
- Energy conversion materials for the space solar power station
- Lightweight and highly robust memristor-based hybrid neural networks for electroencephalogram signal processing
- Method of simulating hybrid STT-MTJ/CMOS circuits based on MATLAB/Simulink

