WANG Dong (王 東),LI Guizhi,SUN Xiaojing,WANG Changqing

(Army Academy of Artillery and Air Defense,Hefei 230031,P.R.China)

Abstract Unmanned aerial vehicles (UAVs) are advantageous for data collection in wireless sensor networks (WSNs) due to its low cost of use,flexible deployment,controllable mobility,etc.However,how to cope with the inherent issues of energy limitation and data security in the WSNs is challenging in such an application paradigm.To this end,based on the framework of physical layer security,an optimization problem for maximizing secrecy energy efficiency (EE) of data collection is formulated,which focuses on optimizing the UAV's positions and the sensors’ transmit power.To overcome the difficulties in solving the optimization problem,the methods of fractional programming and successive convex approximation are then adopted to gradually transform the original problem into a series of tractable subproblems which are solved in an iterative manner.As shown in simulation results,by the joint designs in the spatial domain of UAV and the power domain of sensors,the proposed algorithm achieves a significant improvement of secrecy EE and rate.

Keywords:physical layer security,energy efficiency (EE),power allocation,unmanned aerial vehicle (UAV),data collection,wireless sensor network (WSN)

0 Introduction

Wireless sensor networks (WSNs) are widely applied into commercial and military fields.In the commercial field,the WSNs are deployed for farmland monitoring,intelligent transportation,ecological monitoring and disaster warning,etc.In military field,the WSNs are deployed for battlefield surveillance and awareness,target detection and location,hazardous environment measurement,and so on.In those applications, the WSNs are deployed with infrastructure for long-term needs or deployed without infrastructure for temporary or short-term needs.In the latter case,the data collection is an issue needing to be addressed due to the lack of infrastructure.Unmanned aerial vehicles (UAVs)are advantageous for data collection in such scenarios because of their advantages of low cost of use,controllable mobility and on-demand deployment[1].

Much existing literature concerns the UAV-enabled data collection in the WSNs,and focuses on investigating the efficiency of data collection,the timeliness of the delay-sensitive data, the sleep and wake-up mechanism of sensors,etc.As in Ref.[2],the data collection efficiency is improved by maximizing the minimum average rate,while in Ref.[3],the data collection efficiency is improved by maximizing the average data-rate throughput.In Ref.[4],the timeliness of the delay-sensitive data collected from each sensor is ensured by minimizing the oldest age of the sensing data among the sensors or the average age of the sensing data of all the sensors.The sleep and wake-up mechanism of sensors is studied in Refs[5] and [6] to save limited energy and to prolong the lifetime of the WSNs.

However,to implement the UAV-enabled data collection in the WSNs,other important issues such as the energy limitation and data security also need to be concerned.The critical issue is how to ensure the data is collected by the UAV efficiently and securely under the limited energy.On the one hand,the sensors are always powered by batteries which is energy-limited and adverse to secure data transmission.Thus,it is significant to implement energy-efficient data transmission in the WSNs[7].On the other hand,the harsh environments for open signal propagation and the progressive technologies for security attacks demand comprehensive considerations for data security[8].Physical layer security is an alternative security technology which has attracted increasing attentions.Such a security technology utilizes the physical properties of wireless channels,i.e.,the difference between the main channels and the wiretap channels,to guarantee information security[9].Combined with other physical layer technologies[10],such as power and carrier allocation,beamforming and precoding,user scheduling and cooperation,the physical layer security can ensure information security while improving the performances like transmission efficiency,energy efficiency (EE),etc.

In the WSNs,the UAV-enabled data collection needs to be designed globally to guarantee the security and reliability of data transmission.The good mobility and controllability of the UAV provide the spatial degree of freedom for optimal designs[11].Specifically,the UAV can adaptively adjust its positions to enhance the main channels while to degrade the wiretap channels.It is of particular significance in the scenarios that the eavesdropper can intelligently move to improve its communication quality.In addition,the transmit power of the sensors can also be optimized adaptively to fully use the limited energy.

Motivated by the above investigations,the issues of energy limitation and data security in the WSNs are jointly considered in this paper.Of particular note is that we study the efficient use of energy based on the framework of physical layer security.Specifically,The UAV's three-dimensional (3D) positions and the sensors' power allocation are jointly designed to maximize the secrecy EE while ensuring the data security.For this purpose,a nonconvex and complicated optimization problem is constructed,which focuses on optimizing the UAV's positions and the sensors' power.An iterative algorithm based on the optimization methods of fractional programming and successive convex approximation (SCA) is then proposed,which converts the original problem into a sequence of tractable subproblems in iterations.Simulation results verify that the joint optimization algorithm is effective for improving both the secrecy EE and rate.

The rest of this paper is organized as follows.Section 1 presents the system model and problem formulation.The solution for energy-efficient and secure data collection is elaborated in Section 2.In Section 3,the performance of the proposed algorithm is evaluated numerically.Finally,the conclusions are summarized in Section 4.

1 System model

Consider the scenario that a UAV flies in the sky to collect sensing data fromIground sensors,as shown in Fig.1.An eavesdropper also moves in the sky to wiretap the sensing data from the sensors,which may be UAV,helicopter,controllable air balloon,etc.In practice,the eavesdropper may be not malicious but monitors the sensors' data unintentionally,and thus it is viewed as a passive eavesdropper.

Fig.1 System model

Let (x,y,z) , (xe,ye,ze) and (ui,vi,0) denote the positions of the UAV,the eavesdropper,and theithsensor in the 3D Cartesian coordinate system,respectively.It is assumed that the positions of the eavesdropper and the sensors are known in advance.In practice,the location information can be obtained from basic location database shared by other institutions,or measured by optical reconnaissance or radio direction-finding and localization[12].The distances from theithsensor to the UAV and the eavesdropper are respectively given by

The work considers the flat rural terrain without buildings where the line-of-sight (LoS) links mainly dominate the air-to-ground wireless channels[13-14].In accordance to the investigations in Refs[14,15],in rural environment there is more than 95% probability of LoS links for the UAV at the altitude of 120 m and the horizontal ground distance of 4 km.Thus,the freespace path loss model is adopted to characterize the wireless channels[13-14].The power gains of the channels fromithsensor to the UAV and the eavesdropper can be respectively written ashi=α0andgi=α0,whereα0is the channel power gain at a reference distance of 1 m.

Assume that orthogonal frequency division multiple access (OFDMA) is adopted for the sensors to access the UAV.All terminals are equipped with single antenna.The transmit power of theithsensor is denoted aspi.The received signals at the UAV and the eavesdropper from theithsensor are respectively expressed as[14]

The power consumed for data collection is composed of the UAV-related power and the communication-related power.The UAV-related power consumed for flying depends on its inherent properties,such as aircraft's weight,wing area,rotor radius,air density,etc.The details can be referred to Ref.[16].Therefore,the UAV-related power can be viewed as a constant in practice,which is denoted byPu.The communication-related power is consumed for transmitting data at the sensors and receiving data at the UAV.The transmit power of all sensors is ∑I i=1pi.The power used for receiving data at the UAV is mainly consumed by the hardware circuits of the UAV's receiver,which is also a constant denoted byPc.Therefore,the sum power consumed for data collection can be formulated as

In order to measure the utilization efficiency of energy,define the EE under the consideration of data security,i.e.,secrecy EE,that is the ratio of the secrecy rate throughput to the total power consumption.The secrecy EE of UAV-enabled data collection can be formulated as

whereX?(x,y,z) andP?(p1,p2,…,pI).

In practice,it is expected that the UAV-enabled data collection is performed in an energy-efficient and secure manner.Therefore,the secrecy EE is maximized under the constraints of flying height and maximum power.The problem is formulated as

where,pmaxdenotes the maximum power of the sensors;zmindenotes the minimum altitude of the UAV,which is determined by the altitudes of ground obstacles in the area of the WSN;zmaxdenotes the maximum altitude of the UAV,which depends on the ceiling of the UAV.

2 Solution for energy-efficient and secure data collection

2.1 Transformation for the objective function

The original problem Eq.(11) has an objective function with fractional form,and thus falls into the fractional programming.The fractional objective function can be decoupled into the subtraction of the numerator and the denominator.Specifically,the problem Eq.(11) can be associated with a parameterized problem as[17-18]

Then,solving the problem Eq.(11) is equivalent to finding the optimal solution of the problem Eq.(12)under the condition Eq.(13).By using the Dinkelbach's method[17],the problem Eq.(11) is solved in an iterative manner.To be specific,at the beginning by initialing the auxiliary variableΓwith a given valueΓ(0)while setting iterative indexj= 0 ,the problem Eq.(11) is solved by iteratively solving a series of inner subproblem as

2.2 Introducing slack variables

The problem Eq.(14) is still complicated and is thus needed to be handled further.The completed objective function of the problem Eq.(14) can be rewritten as

The validity of this approach has be verified in Ref.[20].It is also ensured by the following proposition.

Proposition 1The problem Eq.(17) is solved optimally when the conditions of equality are satisfied

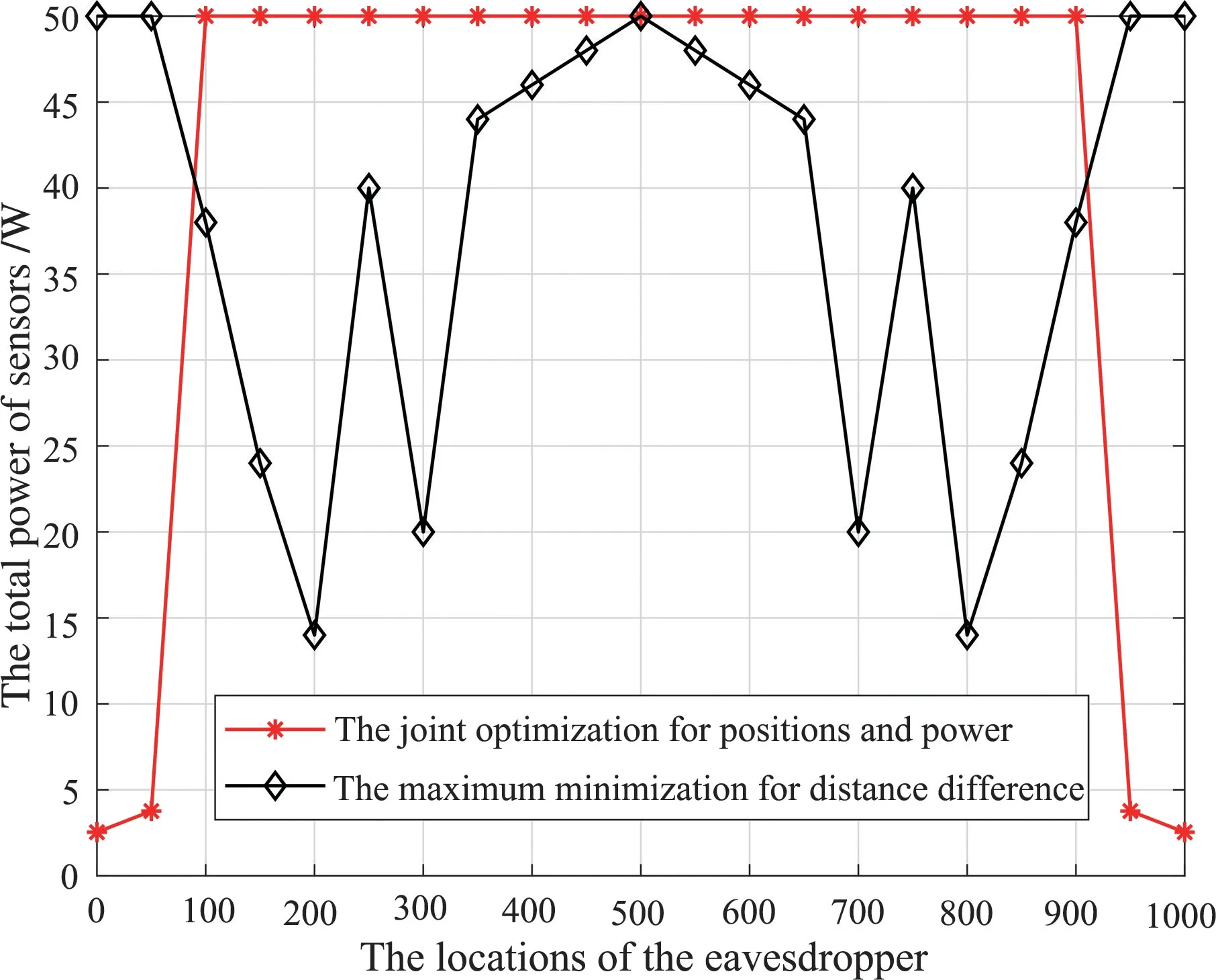
ProofThe proposition is proved by the approach of contradiction.Assume that the optimal solution of the problem Eq.(17) is gotten with the strict inequality conditions,i.e.,+β0pi>aiand

2.3 Successive convex approximation

2.4 Algorithm summary

The proposed algorithm for solving the original problem Eq.(11) is a nested structure of the fractional programming and SCA.Due to the fractional form,the objective function of the original problem Eq.(11) is decoupled into the subtraction of the numerator and the denominator, and then a parameterized problem Eq.(12) is associated with the original problem by viewing the secrecy EEΓas an auxiliary variable.Via solving the parameterized problem Eq.(12) under the condition Eq.(13),the original problem Eq.(11) can be solved.Based on the idea of fractional programming,the parameterized problem Eq.(12) is solved in an iterative manner,and the slack subproblem Eq.(17) is solved at each iteration.It is worth noting that the slack subproblem Eq.(17) is equivalently transformed from the inner subproblem Eq.(14) by variable relaxing.After that,the slack subproblem Eq.(17) is solved iteratively by the SCA,in which the approximated problem Eq.(22) is solved at each iteration.The details of the proposed algorithm are shown in Algorithm 1,where the inner loop is the steps of SCA to solve the slack subproblem Eq.(17) and the outer loop is the steps of fractional programming to solve the parameterized problem Eq.(12).

Algorithm 1 The algorithm for UAV's 3D deployment and sensor's power allocation Input:I,(ui,vi) ,(xe,ye,ze) ,α0 ,σ2 ,pmax ,zmin ,zmax ;Output:(X?,P?) ,Γ?1: Initialize Γ by a suitable value Γ(0) ;2: j: = 0 ,ΔΓ(j): = Γ(0) ;3: While ΔΓ(j) > τ do 4: j: = j +1 ;5: Initialize(X,P,A,B) by some suitable values(X～ (0),P～ (0),A～ (0),B～ (0)) ;6: Calculate F(0) with(X～ (0),P～(0),A～ (0),B～ (0)) ;7: n: = 0 ,ΔF(n): = F(0) ;8: While ΔF(n) > μ do 9: n: = n +1 ;By using the given value Γ(j-1) along with (X～ (n-1),P～ (n-1),A～ (n-1),B～ (n-1)) ,solve the problem Eq.(22) to obtain its optimal solution(X～ (n),P～ (n),A～ (n),B～ (n)) based on the approaches of convex optimization;11: Calculate F(n) with(X～ (n),P～ (n),A～ (n),B～ (n)) ;12: ΔF(n): = F(n) - F(n-1)10:;13: end 14: (X(j),P(j)) = (X～ (n),P～ (n)) ;15: Update Γ(j)based on Eq.(15) by using(X(j),P(j)) ;16: ΔΓ(j): =| R(X(j),P(j)) - Γ(j)Q(P(j)) | ;17: end 18: return(X?,P?): = (X(j),P(j)) ,Γ?: = Γ(j).

3 Simulation results

In this section,numerical simulation is performed to evaluate the performance of the joint optimization algorithm for the UAV's positions and the sensors' power.Specifically,the proposed joint optimization algorithm is compared with a benchmark strategy which deploys the UAV to ensure that more sensors can transmit data securely and reliably.To this end,more sensors should achieve positive secrecy rate,that is the distances between the sensors and the UAV are smaller than the distances between the sensors and the eavesdropper.Therefore, the optimization problem related to the benchmark strategy is formulated as

wheredi-lidenotes the difference between the distance from theithsensor to the UAV and the distance formithsensor to the eavesdropper.To guarantee that the UAV can cover more sensors,the maximum distance difference is minimized by optimizing the position of the UAV.This optimization problem can be easily solved by variable relaxation and SCA[21-22].The algorithm for solving the optimization problem Eq.(23) of the benchmark strategy is referred to as maximum minimization.

The positions of all terminals are depicted in Fig.2.Simulation results show that the UAV's altitudes obtained by the both algorithms are always the minimum altitude.That is because the UAV wants to get closer to the sensors.Therefore,all positions are projected into the horizontal plane to observe the changes.It can be seen that,for guaranteeing data security,the UAV's positions obtained by the both algorithms are adaptively changed with the changes of the eavesdropper's positions.

In Fig.3,the secrecy EE of the both algorithms is compared versus the position changes of the eavesdropper.Thex-axis is the horizontal coordinates of the eavesdropper that corresponds to the eavesdropper's positions.It can be observed that the secrecy EE achieved by the joint optimization outperforms that achieved by the maximum minimization.At the outermost points of the figure, the joint optimization algorithm achieves more higher secrecy EE than the maximum minimization does.The reason is that the relative positions of the UAV,eavesdropper,and sensors result in better channel qualities to support the energy-efficient and secure data collection.

Fig.3 Secrecy EE versus the position changes of the eavesdropper

Fig.4 plots the secrecy rate throughput versus different positions of the eavesdropper.It can be seen that the total secrecy rate of the joint optimization is also higher than that of the maximum minimization.The curve of the secrecy rate throughput fluctuates violently because the move of the eavesdropper leads to significant variations of channel qualities.Just because of the optimized positions of the UAV and optimized power of the sensors against channel variations,the joint optimization achieves a better performance of the secrecy rate throughput.

In Fig.5,the total power consumed by the two algorithms is illustrated under different positions of the eavesdropper.It can be seen that,although the secrecy EE and total secrecy rate of the joint optimization outperform that of the maximum minimization,the total power consumed by the joint optimization is not always more than that consumed by the maximum minimization.Especially at the outermost points of Fig.5,the joint optimization algorithm consumes less power but achieves higher secrecy rate and EE.

Fig.5 Total power versus the position changes of the eavesdropper

In Fig.5,the power curve obtained by the maximum minimization fluctuates dramatically because only a part of sensors are sometimes selected to transmit data and the residual sensors keep sleeping to save energy.But such a simple strategy of sensor selection for saving energy is suboptimal from the perspective of secrecy EE.The joint optimization algorithm can achieve higher secrecy EE due to the global designs of spatial domain and power domain.It is worth noting that the proposed algorithm also has the implicit function of sensor selection.To be specific,it is revealed by the simulation results that,if the channel quality of a sensor is too bad to support secure data transmission,the sensor would not be allocated any power.

4 Conclusions

Using the UAV to collect data in the WSNs faces two critical issues of energy limitation and data security.To cope with these issues,this paper proposes a joint optimization algorithm for the UAV's 3D positions and the sensors' power allocation to improve the secrecy EE and to ensure the data security simultaneously.The resulting optimization problem is nonconvex and difficult to solve.The optimization approaches of the fractional programming and SCA are then adopted to transform the original problem into a series of tractable subproblems which are successively solved in iterations.Duo to the global designs of spatial domain and power domain,the proposed optimization algorithm can improve the secrecy EE and the secrecy rate of the data collection.Simulation results show that both the secrecy EE and secrecy rate achieved by the joint optimization algorithm are higher than that achieved by the maximum minimization.