YANG Xin(楊 欣), ZHOU Wei(周 偉)

School of Mathematics and Physics, Lanzhou Jiaotong University, Lanzhou 730070, China

Abstract：The generalized dynamic Tullock contest model with two homogeneous participants is established, in which both players have the same valuation of winning rewards and losing rewards. Firstly, the unique symmetric equilibrium point of the system is obtained by calculation and its local stability condition is given based on the Jury criterion. Then, two paths of the system from stability to chaos, namely flip bifurcation and Neimark-Sacker bifurcation, are analyzed by using the two-dimensional parametric bifurcation diagram. Meanwhile, the abundant Arnold tongues in the two-dimensional parametric bifurcation diagram are analyzed. Finally, the phenomenon of multistability of the system is illustrated through the basin of attraction, and the contact bifurcation occurs during the evolution of the basin of attraction with varying parameters.

Key words：Tullock contest; Arnold tongue; contact bifurcation; chaos; coexistence of attractor

0 Introduction

Contest theory is the study of situations in which two or more players compete through expending effort to win a reward or avoid punishment. Many phenomena in the real world can be studied within the framework of contest theory, such as election campaigns, lobbying, rent-seeking, sports, examinations, competitions for technological development, relative punishments within corporations, arms races between nations and wars. Tullock proposed the concept of contest success function (CSF)[1], which referred to the corresponding relationship between players’ efforts and their probability of winning. According to the CSF, the contest can be divided into all-pay auctions, Tullock contests and Lazear-Rosen contests. A generalized Tullock dynamic contest model based on the Tullock contest theory is established in this paper.

Scholars at home and abroad have done a lot of research on the Tullock contest model from static and dynamic aspects. For static models, the existing literature focused on the existence and characteristics of Nash equilibrium. Peréz-Castrilloetal.[2]reflected on the basic mode of “efficient rent-seeking” and gave a complete description of pure strategy equilibrium. Nti[3-4]considered the Tullock rent-seeking game under the condition of asymmetric valuation and established the sufficient and necessary conditions of the unique pure strategy Nash equilibrium. Alcaldeetal.[5]proved the existence of mixed strategy equilibrium. Fengetal.[6]provided a different method to establish the uniqueness of the equilibrium between two players with an asymmetric valuation in the Tullock contest with discriminatory power between 1 and 2. However, the study of the static model has some limitations. In the actual economic environment, factors such as market demand and market supply, are constantly changing, leading to dynamic changes in the overall market environment. Therefore, the use of the dynamic model to simulate the Tullock contest has attracted the attention of some scholars. Xuetal.[7]studied the asymptotic stability of equilibrium in dynamic rent-seeking games. Bischietal.[8]studied the dynamic rent-seeking game with two bounded rational participants and analyzed the basin of attraction with a special structure generated by the focus. Schmidt[9]established a model extending to asymmetric bonus valuation and endogenous reward and studied the local stability of Nash equilibrium in adjustment speed and reward level. Zhangetal.[10]studied the dynamic behavior of asymmetric competition models with bounded rationality. By studying the local stability and bifurcation of the equilibrium point, the stability conditions are given, and it is proved that the asymmetric competition model inherently generates two paths to chaos：flip bifurcation and Neimark-Sacker bifurcation. Yuetal.[11]considered a dynamic rent-seeking game involving the decision-maker’s cost and competitive intensity. The local asymptotic stability of the Nash equilibrium is proved under political conditions and rent-seekers with incomplete information sets.

However, most of the existing literature focused on the Tullock rent-seeking game or the standard Tullock contest model. Compared with the reward mechanism, the punishment mechanism has received less attention. In addition, most of the literature focused on the local stability of equilibrium points, lacking characterization of complex dynamic behaviors that may exist in dynamic models, such as the coexistence of attractors[12]and global bifurcation[13]. Therefore, the punishment mechanism is introduced in this paper, and the generalized dynamic Tullock contest model which is more consistent with the actual contest market environment is established. The unique equilibrium point of the system is obtained through calculation, and its local stability is analyzed by utilizing nonlinear dynamics theory and Jury criterion[14]. The effects of adjustment speed and contest cost on the stability of the system and the evolution process of the system under the change of parameters are analyzed by one-dimensional and two-dimensional parametric bifurcation diagrams. Finally, the global dynamic behavior of the system is analyzed by means of the basin of attraction.

1 Modeling

We consider a Tullock contest involving two players, in which players compete against each other by expending irreversible effort to win a reward or avoid punishment. Assuming that two players have the same valuation of the winning reward and the losing reward,i.e., they are symmetric, the two players are represented byi(i=1, 2).The winning reward isW, andW>0; the losing reward isL, andL∈R.The winning reward is higher than the losing reward,i.e.W>L.The CSFpifor a Tullock contest withnplayers[15]is

(1)

wherexiis the effort spent by the player;ris called discriminatory power and it measures the effectiveness of the player’s effort in determining the probability of winning,i.e., the accuracy of the contest itself. Whenr→∞,the Tullock contest is infinitely close to an all-pay auction. Asrincreases, the accuracy of the contest increases. To simplify the calculation, the discriminatory powerris supposed to be 1, so the CSF adopted in this paper is

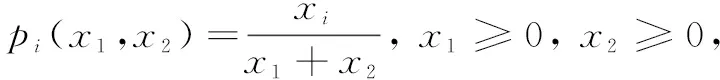
(2)

It is assumed that the cost function of both players is a linear function of expenditure, and the unit cost of the two players participating in the competition is equal, that is, the players are homogeneous, but the cost of each player is different when the contest succeeds or fails. Therefore, the cost function can be expressed by

(3)

Therefore, the payoff of playeriis

(4)

wherec1andc2respectively represent the cost of success and failure in a contest. In order to ensure that the player does not have the motivation to spend infinite effort, we set such conditions：the player’s efforts have a direct negative impact on his reward for winning and a non-positive direct impact on his reward for failure, that isc1>0 andc2≥0.Based on the CSF and the reward the player receives, we can further calculate the expected revenue of the player as

Πi(x1,x2)=pi(W-c1xi)+(1-pi)(L-c2xi).

(5)

Thus, the marginal revenues of the two players are

(6)

It is difficult for two players to obtain complete information about the market, so both players are assumed to be bounded rational. Based on the gradient adjustment mechanism[16], each player uses the local estimate of marginal expectation to update his effort expenditure at timet, so the following dynamic contest model can be established.

(7)

wherek1(>0) andk2(>0) represent the adjustment speeds of player 1 and player 2 respectively.

2 Equilibrium Point and Local Stability

The following equations can be obtained by settingxi(t+1)=xi(t) (i=1, 2) in system (7).

As system (7) is not defined in (0, 0), the unique equilibrium point is

Because (W-L)/(3c1+c2)>0,((W-L)/(3c1+c2), (W-L)/(3c1+c2)) is an internal equilibrium, also known as the Nash equilibrium.

In order to study the stability of the Nash equilibrium, the Jacobian matrix[17]Jof system (7) is given as

where

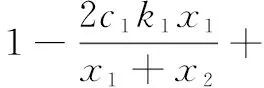
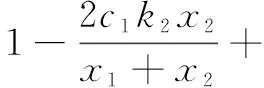
Substituting the Nash equilibrium pointE*into the Jacobian matrix, we can get

The trace and determinant of the Jacobian matrixJ(E*) can be obtained as

T=(1-c1k1)+(1-c1k2)=2-c1(k1+k2),

When and only when the eigenvalues of the Jacobian matrix are inside the unit circle of the complex plane, the Nash equilibrium point is in a stable state. Therefore, the following Jury’s conditions are satisfied:

Proposition1The Neimark-Sacker bifurcation does not occur at the Nash equilibrium pointE*.

ProofIt is easy to know that the characteristic equation of the Jacobian matrix corresponding toE*is

F(λ)=λ2-λT+D.

The discriminant of the characteristic equation can be written as

Ask1>0,k2>0, obviously Δ>0, which means that the system has two mutually distinct real eigenvalues at the Nash equilibrium pointE*and does not produce complex eigenvalues. Therefore, the Neimark-Sacker bifurcation does not occur in the system.

Proposition2The Nash equilibrium pointE*is locally stable as long as the system parameters satisfy the following condition

ProofTo make the equilibrium point stable, the three conditions of the Jury criterion should be satisfied. A simple calculation shows that to make the three conditions hold at the same time, the above inequality should be satisfied.

3 Numerical Simulation and Complexity Analysis

3.1 Bifurcation analysis

We study the complex dynamic behavior of the system by numerical simulation. In the two-dimensional parametric bifurcation diagram shown in Fig. 1(a), the multi-dimensional parameters in the system are fixed asW=10.369 3,L=1.420 3,c1=0.837 5 andc2=1.796 0. In Fig.1(a), the color bar on the right indicates the number of different periods, and black is used to indicate aperiodic motion (chaotic and quasi-periodic), represented by the number 30. The olive-green area in the lower left corner represents the stable area of the system under this set of parameters, and it can be found that the system can enter chaos by means of flip bifurcation. When other parameters are fixed, the system loses stability as the adjustment speedk1increases, which means that within a certain range, a smaller adjustment speed is more conducive to maintaining the stability of the system. To further analyze the influence of parameters on the stability region, stability curves corresponding to different values of the parameterc1are drawn on the plane (k1,k2).The values of the parameterc1are 0.837 5, 0.937 5 and 1.000 0 respectively as shown in Fig. 1(b). It was found that the stability region of the system would gradually decrease with the increase of the parameterc1.

As shown in Fig. 2(a),W=13.258 0,L= -3.510 1,c1=0.167 6 andc2=1.502 2. It can be observed that a large number of V-shaped isoperiodic structures are embedded in the aperiodic motion indicated by black. These V-shaped periodic islands are also called Arnold tongue[18], and they are adjacent to the Neimark-Sacker bifurcation line[19](the olive green-black boundary). Aperiodic solute ions and periodic solutions appear alternately with the increase of adjustment speeds. In addition, Fig. 2(b) is a local enlargement of the region [1.8, 4.3]×[3.5, 5.6] in Fig.2(a), and the number of cycles increases to 100. As can be seen from Fig. 2(b), the area of these Arnold tongues increases with the increase of adjustment speed, resulting in a wider interval of mode-locked. When the threshold value is reached, these tongues overlap and intertwine together, leading to chaos eventually.

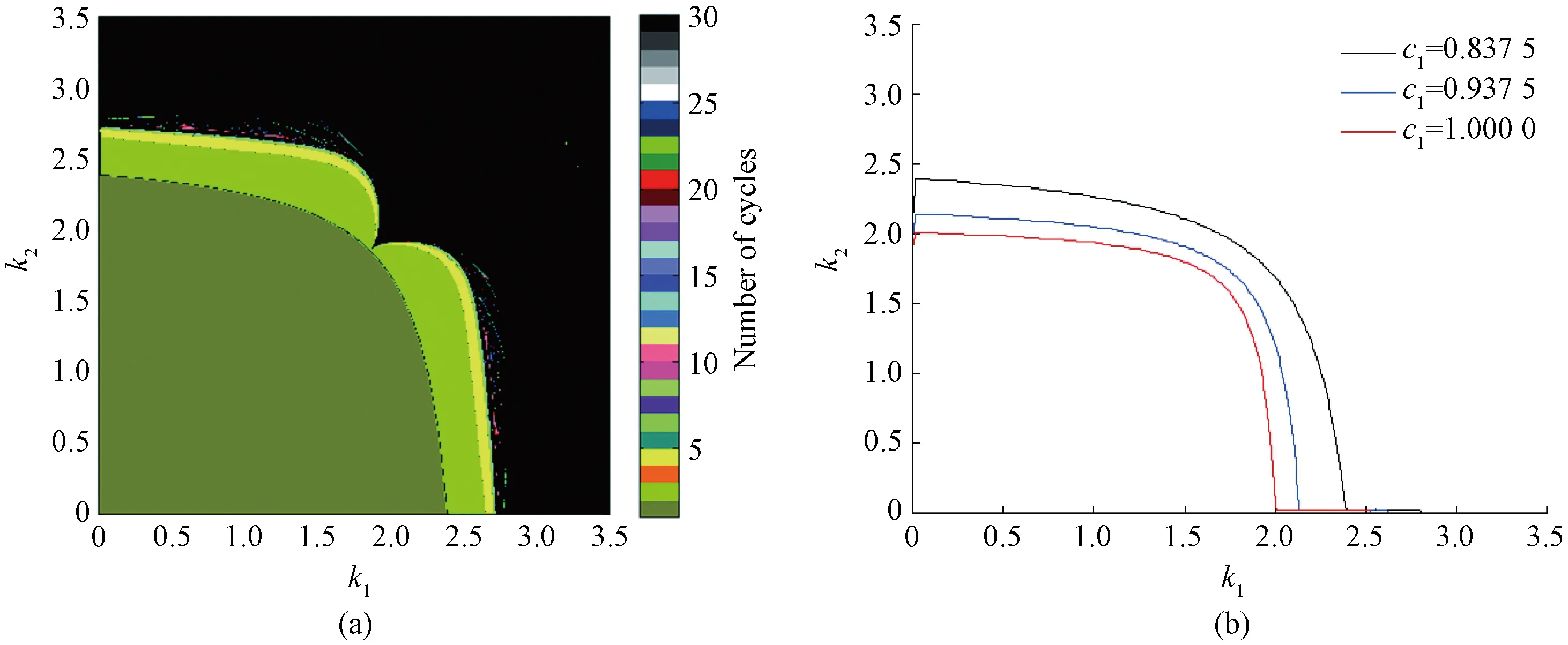
Fig.1 Stability analysis：(a) two-dimensional parameter bifurcation diagram; (b) stability curves at different c1

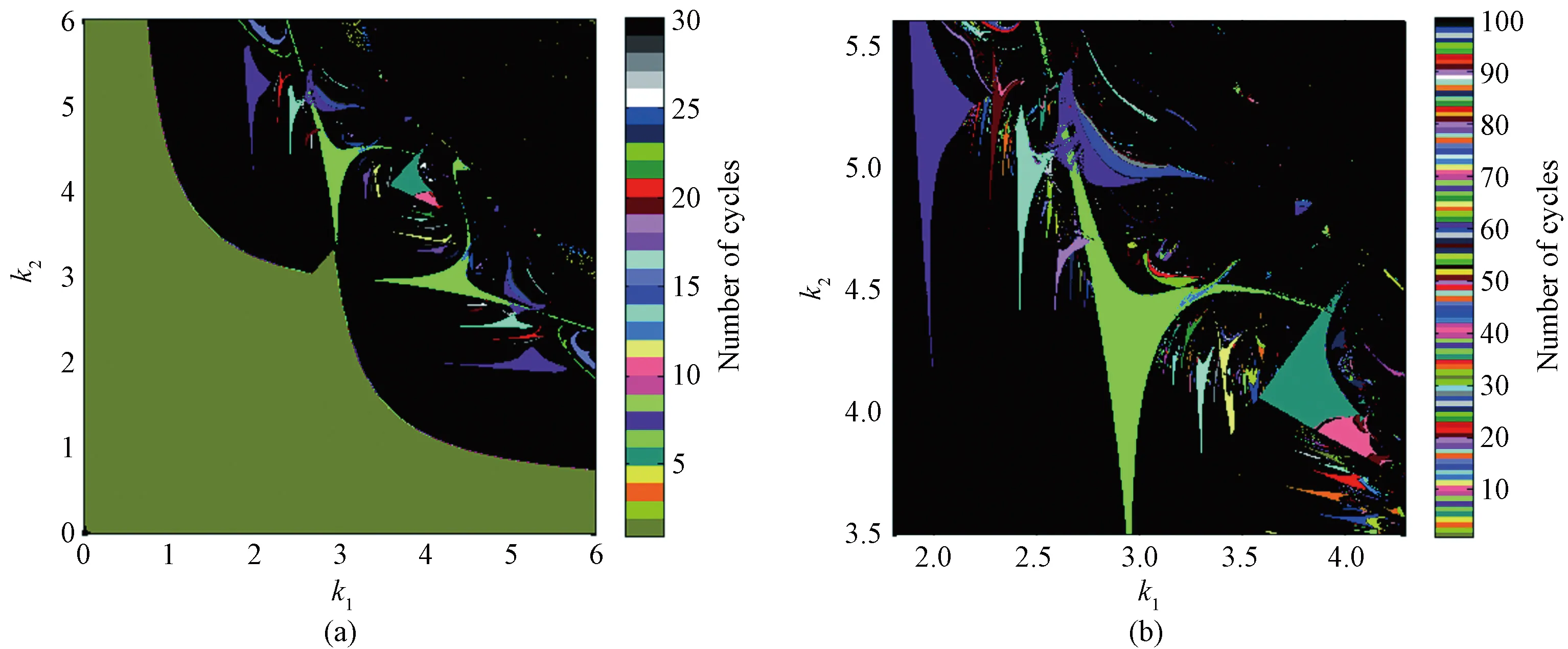
Fig.2 Two-dimensional parametric bifurcation diagram：(a) bifurcation diagram of k1-k2 plane; (b) local enlargement diagram of Fig.2(a)

Figure 3 shows the one-dimensional parametric bifurcation diagrams of the system changing with the adjustment speedk1.Figure 3(a) is obtained by fixingk2=2.603 9 based on Fig. 2(a), which shows that the first bifurcation occurs whenk1=0.480 0, and the system transitions from period-2 state to chaos after flip bifurcation. Figure 3(b) is obtained by fixingk2=5.112 0 based on Fig. 2 (a), it can be seen that Neimark-Sacker bifurcation occurs atk1=0.840 0, and the system directly enters chaos from the stable period-1. The chaos continues untilk1=1.852 0, a 7-period lock is generated. By increasingk1further, the system enters chaos again and returns to a periodic state through inverse Neimark-Sacker bifurcation atk1=2.865 0, and then enters chaos again through period-doubling bifurcation. This means that after the economic system gets out of the cyclical behavior, if the players do not reduce the adjustment speeds in time and let them continue increasing, both players will be directly forced to exit from the market in such a chaotic market.

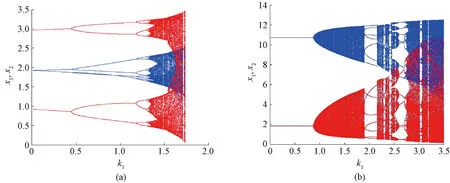
Fig.3 Bifurcation diagrams of k1 at different k2：(a)k2=2.603 9; (b)k2=5.112 0

3.2 Basin of attraction and multistability

The local stability analysis given above only focuses on a small neighborhood near the equilibrium point and cannot explain the change of model properties when system parameters change. Therefore, to further study the long-term dynamic behavior of the system under given initial conditions, the global analysis of the system is carried out by using the basin of attraction.

The fixed system parameters areW=25.002 3,L=15.258 0,c1=0.384 8,c2=1.061 4 andk2=3.631 6. Figure 4 shows the evolution of the basins of attraction with the change of the adjustment speedk1.The cyan region is the region of attraction of the black attractor, representing the bounded trajectory region. Any initial condition taken in this region can converge to the black attracting set after several iterations, while the dark blue region is the escape region, representing the divergent trajectory (or negative trajectory) region, and any initial condition taken in this region can become divergent. This means that we can use the above analysis to roughly predict the future of the system.

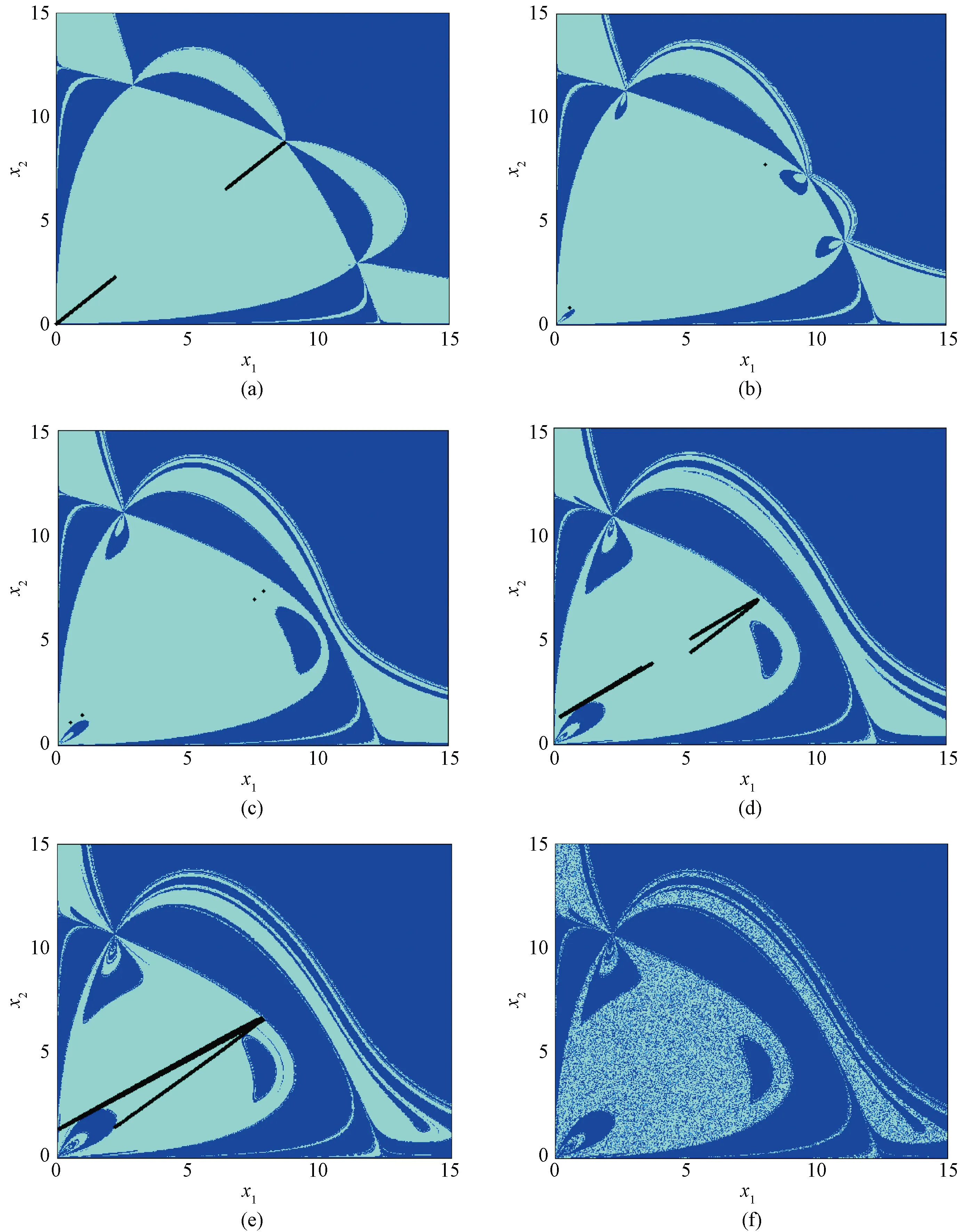
Fig. 4 Evolutionary process of basins of attraction under different adjustment speeds when W=25.002 3, L=15.258 0, c1=0.384 8, c2=1.061 4 and k2=3.631 6：(a) k1=3.762 4; (b)k1=3.831 3; (c)k1=4.008 7; (d)k1=4.359 4; (e)k1=4.534 0; (f)k1=4.535 4

In Fig. 4(a),k1=3.762 4, there are two weak attractors in the Milnor sense[20], the main region of the attraction domain is approximately in the shape of a rounded triangle, and the basin of attraction is symmetric about diagonal. In Fig. 4(b),k1increases to 3.831 3, two weak attractors evolve into period-2 attractors, and the main region of the attractors is accompanied by the appearance of the “hole”, the basin of attraction loses symmetry. Ask1increases to 4.008 7, period-2 attractors evolve into period-4 attractors through period-doubling bifurcation, and the area of the “hole” increases as shown in Fig. 4(c). In Fig. 4(d),k1=4.359 4, then the period-4 attractor evolves into two pieces of chaotic attractors. In Fig. 4(e),k1further increases to 4.534 0, and the two chaotic attractors expand and fuse into a piece of chaotic attractors which almost touches the boundary of the domain of attractors, and a contact bifurcation may occur. In Fig. 4 (f),k1=4.535 4, contact bifurcation happens, so the chaotic attractor is destroyed, and the feasible region is full of “ghosts” of the “just died” chaotic attractor.

Figure 5 shows a set of basins of attraction containing the coexistence of attractors with the change of adjustment speedk1.Black and red represent different attractors and the parameters are fixed asW=25.175 3,L=5.271 0,c1=0.186 6,c2=1.781 1 andk2=3.587 4. In Fig. 5(a),k1=2.518 0, an invariant cycle coexists with an annular chaotic attractor formed by the Neimark-Sacker bifurcation. In Fig. 5(b),k1=3.172 0, the invariant cycle evolves into ten pieces of chaotic attractors in the shape of “fireworks” and the annular chaotic attractor evolves into a piece of chaotic attractors with the increase ofk1.In Fig. 5(c),k1=3.548 0, the chaotic attractor evolves into a piece of chaotic attractors, while the red attractor hardly changes. Because two chaotic attractors are in contact with their own boundary of the domain of attraction, contact bifurcation occurs in the system at this time, resulting in the unclear boundary of the domain of attraction of the two groups of coexisting attractors, and the blue region and light blue region infiltrate each other. In Fig. 5(d),k1continues to increase to 3.588 9, and both two pieces of chaotic attractors split into eight pieces of chaotic attractors. It can be seen from the above analysis that the changes in initial conditions and parameters make the system present different dynamic behaviors. Although the change of initial conditions and parameters leads to different dynamic behaviors of the system, we can still roughly predict the future of the system through the above analysis. Economically, players can make corresponding strategy adjustments to achieve their long-term stability and benefit from it.

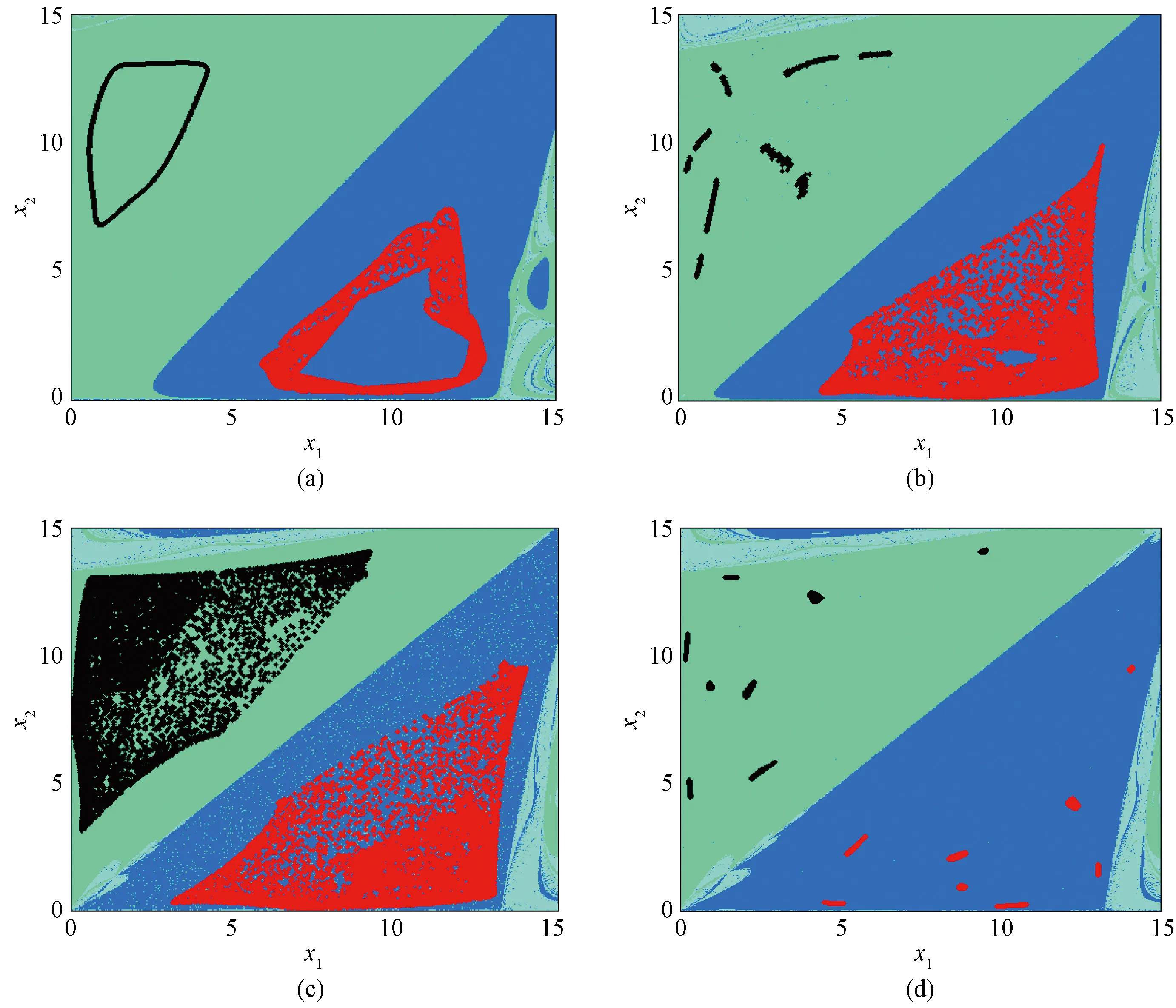
Fig. 5 Evolutionary process of basins of attraction under different adjustment speeds when W=25.175 3, L=5.271 0, c1=0.186 6, c2=1.781 1 and k2=3.587 4：(a)k1=2.518 0; (b)k1=3.172 0; (c)k1=3.548 0; (d) k1=3.588 9

4 Conclusions

In this paper, to maximize the expected benefits of players, the symmetric dynamic Tullock contest model is discussed and the existence and stability of equilibrium points are analyzed. One-dimensional parametric bifurcation diagrams and two-dimensional parametric bifurcation diagrams are used to study the system’s path into chaos and the influence of parameters on the stability of the system. The results show that the system has two paths into chaos, namely flip bifurcation and Neimark-Sacker bifurcation, and the smaller the adjustment speed and contest cost, the more stable the system. This means that to ensure the long-term stability of the market, players should choose the smaller adjustment speed and contest cost. Finally, the global dynamic behavior of the system is studied, and it is found that contact bifurcation occurs when the parameters exceed the threshold values, and the system can present different kinds of attractor coexistence phenomena.