Yong-Ge Yang(楊勇歌), Yun Meng(孟運(yùn)), Yuan-Hui Zeng(曾遠(yuǎn)輝), and Ya-Hui Sun(孫亞輝),2,?

1School of Mathematics and Statistics,Guangdong University of Technology,Guangzhou 510520,China

2State Key Laboratory for Strength and Vibration of Mechanical Structures,Xi’an Jiaotong University,Xi’an 710049,China

Keywords: hybrid vibration energy harvesting, narrow-band random excitation, multi-scales method, viscoelastic material,stochastic bifurcation

1.Introduction

Sustainable technologies that harvest energy from environmental vibrations for power generation have received considerable attention in recent years.[1–4]Vibration energy harvesters (VEHs) with ability to harvest electrical energy from environmental vibration are a good potential technology to provide continuous electrical energy instead of batteries with limited lifespan.[5]Piezoelectric,[6]electromagnetic,[7]electrostatic[8]and triboelectric[9]transductions are the main technologies for converting environmental vibration into electric energy.To increase the energy conversion efficiency,a hybrid piezoelectric and electromagnetic energy harvesting system (EHS) has been developed.Challaet al.[10]developed the hybrid piezoelectric and electromagnetic energy harvesting technology based on a single frequency.Karamiet al.[11]employed approximation methods to study variations of damping and excitation frequency in a nonlinear hybrid EHS.Liet al.[12]studied the mean output power and power spectral density of a hybrid piezoelectric and electromagnetic EHS.Mokemet al.[13]proposed a hybrid device combining piezoelectric and electromagnetic transduction under colored noise.Fanet al.[14]investigated a hybrid piezoelectric and electromagnetic EHS under low-frequency and multi-directional excitations.Taking advantages of the stochastic averaging technique, Sunet al.[15]found that a hybrid vibration EHS can produce a mean output power higher than a piezoelectric or electromagnetic system alone.

Since random factors exist widely in most realistic environments and can affect the dynamical behaviors of a system,it is necessary to investigate the system under random excitation.Ronget al.[16]studied the principal resonance of the Duffing oscillator under deterministic and narrow-band random excitation by taking advantage of the multi-scales method and the qualitative analysis method.Liuet al.[17]proposed a quasi-conservative stochastic averaging method to investigate the probabilistic responses of a nonlinear VEH driven by exponentially correlated Gaussian colored noise.Jinet al.[18]applied the multi-scales method to study a Duffing-type energy harvester with time-delay circuits under narrow-band random excitation.Using the stochastic averaging method, Huanget al.[19]studied a strongly nonlinear light damping system with a fractional derivative under Gaussian white noise excitation.Xiaoet al.[20]found that correlated noise can enhance efficiency of a piezoelectric energy harvester.To improve energy harvesting efficiency,Zhanget al.[21]carried out theoretical and numerical studies on an electromechanically coupled VEH under colored noise and periodic excitation.By utilizing the implicit harmonic balance method and the Gaussian closure method,Zhuet al.[22]discussed the periodic response of a Duffing oscillator under harmonic and random combined excitation.Shiet al.[23]studied an asymmetric stochastic resonance system with time-delayed feedback driven by non-Gaussian colored noise.Linet al.[24]invesigated the bursting oscillation and energy harvesting efficiency of a piezoelectric energy harvester in rotational motion under low-frequency excitation.Under Gaussian white noise excitation, Suet al.[25]presented a vibration EHS with rigid and elastic impacts.Jianget al.[26]designed an electromechanical broadband energy harvester with one-to-one internal resonance.

Viscoelastic materials, in contrast to conventional elastic materials, can not only store elastic potential energy but also dissipate energy.[27]Furthermore, viscoelastic materials with viscoelastic properties like stress relaxation and creep are more suitable for describing practical problems, so they are widely used in physics, mathematics, engineering, and other fields.[28–31]Xuet al.[32]investigated a narrow-band noise system with fractional damping and viscoelastic term.Guoet al.[33]discussed the stochastic responses of an EHS with viscoelastic material excited by Gaussian white noise.Wuet al.[34]analyzed the initial boundary value problem for the viscoelastic equation in a bounded region.By utilizing the harmonic balance method and the stochastic averaging method,Xuet al.[35]obtained the responses of a viscoelastic system under the combination of deterministic harmonic and random excitation.Floriset al.[36]studied the stability of hingedhinged viscoelastic column under non-zero mean stochastic axial force.Deno¨elet al.[37]carried out the multiple timescale spectral analysis of a single-degree-of-freedom viscoelastic system with a fractional derivative.

Recently,there are several papers[38–41]focused on vibration EHSs with viscoelastic materials.In Refs.[38,39]the authors adopted the stochastic averaging method to investigate EHSs.In Refs.[40,41] the authors studied a single type of piezoelectric EHSs by applying the multi-scales method.The vital difference between our study and the above-mentioned studies is that we consider a hybrid vibration EHS subjected to narrow-band noise excitation by employing the multi-scales method.

The remainder of this paper is organized as follows.In Section 2,we present the basic mathematical model of the hybrid piezoelectric and electromagnetic EHS with viscoelastic material under narrow-band noise excitation.In Section 3,the approximate solutions for the hybrid vibration EHS are obtained by employing the multi-scales method.The analytical results are verified by numerical simulation results obtained with the Monte Carlo method.Moreover, the stochastic responses and the stochastic bifurcation phenomena of the system are further explored.In Section 4,the influence of the system parameters on mean-square electric voltage,mean-square electric current and mean output power is discussed.Finally.the conclusions are given in Section 5.

2.Mathematical model

So far, several different nonlinear vibrational energy harvesters with high conversion efficiency have been designed.[42–44]Taking the hybrid piezoelectric and electromagnetic energy harvester as an example, it can be modeled as a mass-spring-damping system coupled with piezoelectric and electromagnetic circuits under fundamental acceleration excitation.[45–47]The simplified structural schematic and the simplified representation of the piezoelectric and electromagnetic circuits are shown in Figs.1(a)–1(c),respectively.

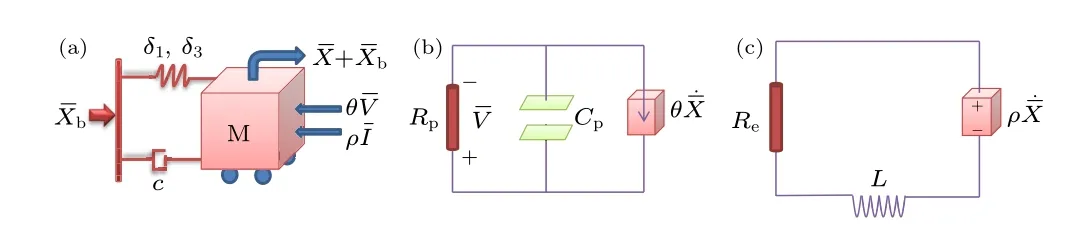
Fig.1.(a)A simplified structural schematic of the hybrid VEH with(b)piezoelectric and(c)electromagnetic circuits.

In order to illustrate the mechanical property of viscoelastic material in damping structure, a hybrid VEH with viscoelastic material[48,49]is presented in Fig.2.

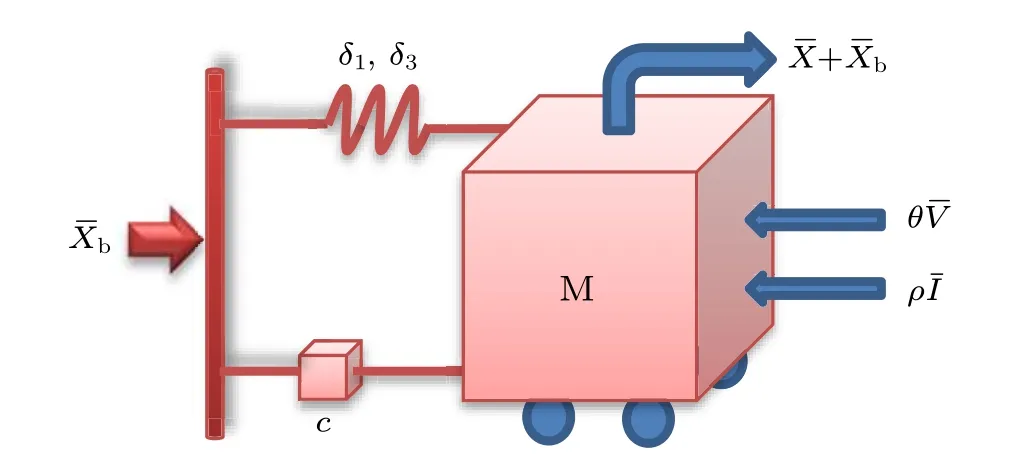
Fig.2.A simplified representation of the hybrid VEH with viscoelastic material.

The governing equations of the hybrid VEH can be written in the following general form:

where the symbols for the hybrid vibration EHS are listed in Table 1.

We introduce the dimensionless transformations as follows:

Then the dimensionless form of Eq.(1)is given as

The definitions of symbols are listed in Table 2.

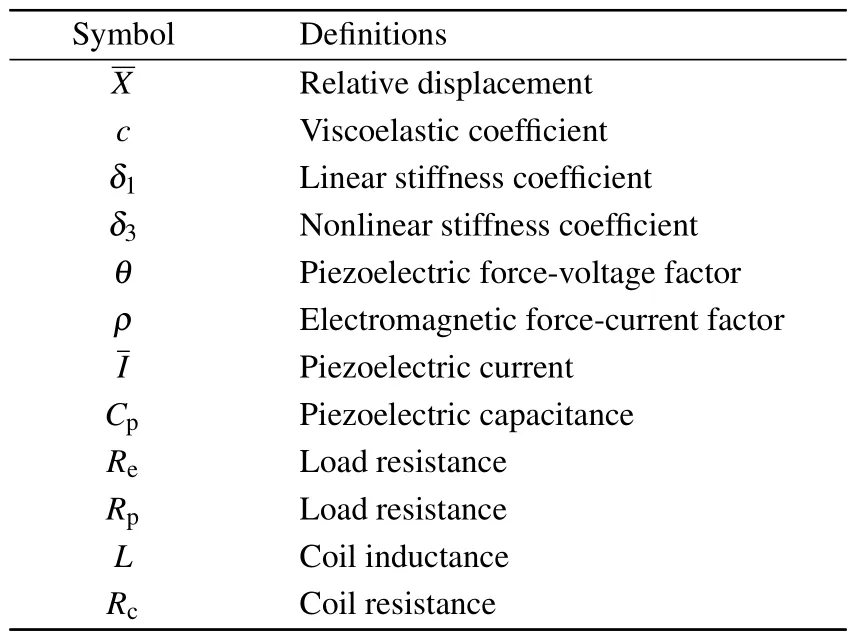
Table 1.Symbols and definitions.

Table 2.Symbols and definitions.

Here,-¨xbis equivalent to noiseξ(τ),which stands for a narrow-band random process and can be written as[50]

whereγis the intensity of the random excitation,W(τ) is a standard Wiener process,ωdenotes the excitation frequency,and ?Fis the deterministic amplitude.

The viscoelastic termH(βω,x,τ)is derived as[32]

According to Ref.[51], the power spectrum densitySξ(ω)ofξ(τ)can be expressed as

where the random processξ(τ)can be considered as a narrow band process whenγis small.

3.Response analysis

For convenience,we introduce the following transformations:

Then,substituting Eqs.(4)and(7)into Eq.(3),we have

in which the over-dot prime represents the derivative with respect to the time variableτ.In this paper,the multiple scales method[16,18,52]is employed to investigate the responses of the system (3).Taking advantage of the modified multi-scales method,we introduce fast and slow time scales as follows:

Introducing

the ordinary time derivatives can be transformed into partial derivatives as

The approximate solutions of Eq.(8)are given as follows:

Substituting Eqs.(10)–(12)into Eq.(8),and equating the coefficients ofε0andε1to zeros,the formulas at the first order can be written as

The formulas in the second order can be given as

In Eq.(14a), according to the property of the standard wiener process,we obtain

The general solution of Eq.(13)can be written as

whereAis the complex conjugate ofA,Bis the complex conjugate ofB,Cis the complex conjugate ofC.

Substituting Eqs.(16a)and(16b)into Eq.(13b),Bis derived as

whereA(T1)is the slowly varying amplitude of the solution.

Similarly,substituting Eqs.(16a)and(16c)into Eq.(13c),we can obtain the relationship betweenCandAas follows:

The viscoelastic termH(βω,x0,T0)is written as

where c.c.denotes the conjugate term.

Substituting Eqs.(16)–(19)into Eq.(14a)and eliminating the secular terms,we obtain

Letting

where

The excitation frequencyΩclose to the system frequencyωis determined in order to study the primary resonance,that is,

Substituting Eqs.(21)and(22)into Eq.(20),we arrive at

The differential equations for the amplitudeaand phaseηwith regard to the slow timescaleT1are obtained by splitting Eq.(23)into the real and imaginary portions

Therefore, by solving Eq.(24), combining Eqs.(16a)–(18),(21)–(22)and(24),the first-order approximate solutions of the hybrid vibration EHS(3)can be written as

In particular, we focus on the fit between the theoretical and the numerical results for the amplitude-frequency responses,which validates the analytical approach described above.

Whenγ=0,the deterministic steady-state solutionsa=a0andη=η0of Eq.(24)satisfyD1a=0 andD1η=0,then Eq.(24)becomes

After eliminatingη0from Eq.(26), the equation of amplitude-frequency responses is obtained as follows:

with

Whenγ/=0,in order to determine the stability of the nontrivial steady state solutions,we let

wherea1andη1are the perturbation terms on the deterministic situations.

Substituting Eqs.(26)and(28)into Eq.(24)and neglecting the nonlinear terms,the It?stochastic differential equations are obtained as follows:

where

Under the steady-state situation,it is known that

whereE(·)denotes the mathematical expectation.

Combining Eqs.(29)and(30),one can obtain

Solving Eq.(31), we can obtain the first-order and secondorder steady-state moments(FSSMs)ofa1andη1as

where

Therefore,the FSSMs of the steady-state solutions to Eq.(24)are given as

In the steady-state case,the voltage and current of the response are obtained by Eqs.(25b)and(25c),respectively,

Taking the expectation on both sides of Eq.(34), the FSSMs of the voltage and current amplitude are

Since the mean output power of the hybrid vibration EHS is the sum of the mean output power of the electromagnetic and piezoelectric circuits, the mean output power can be expressed as

The numerical solution to Eq.(8) is calculated by the fourth-order Runge–Kutta algorithm.In the present numerical computation,we take parameters asε=0.1,β=3,ω=1.5,F=1.6,β1=1,μ=2,q=1.2,g=1,λ1=3,λ2=2.

Fig.3.The FSSMs E(a)(a)and E(a2)(b)of amplitude-frequency response(γ =0.01, β =3).Red dots denote the numerical results, blue lines stand for the approximate analytical results.

The numerical results in Fig.3 are presented to verify the theoretical results obtained from Eqs.(32) and (33).The FSSMs for random excitationγ=0.01 are displayed in Fig.3,and it can be seen that the numerical and approximate analytical results are in good agreement with each other.

In the following numerical simulation, the time history and phase trajectory of system(8),beginning from initial valuesx(τ) = 0.7, ˙x(τ) = 0.3,v(τ) = 0.01,i(τ) = 0.01, with different noise intensitiesγand detuning frequenciesσ, are shown in Fig.4.When the intensity of random excitationγincreases, the output responses of displacementx(τ) and velocity ˙x(τ) change, and the phase trajectory transforms from a limit cycle into a diffused limit cycle in Fig.4.At different detuning frequenciesσ, the responses of displacementx(τ),velocity ˙x(τ), voltagev(τ), and currenti(τ) are depicted in Fig.5,where the responses of the system increase slowly and then sharply decrease inσ ∈(2.5,3.0).Therefore, when the detuning frequencyσgradually increases,the jump can occur.

Fig.4.Time history and phase portraits for the deterministic system(σ =1): [(a),(b)]γ =0,[(c),(d)]γ =0.05.

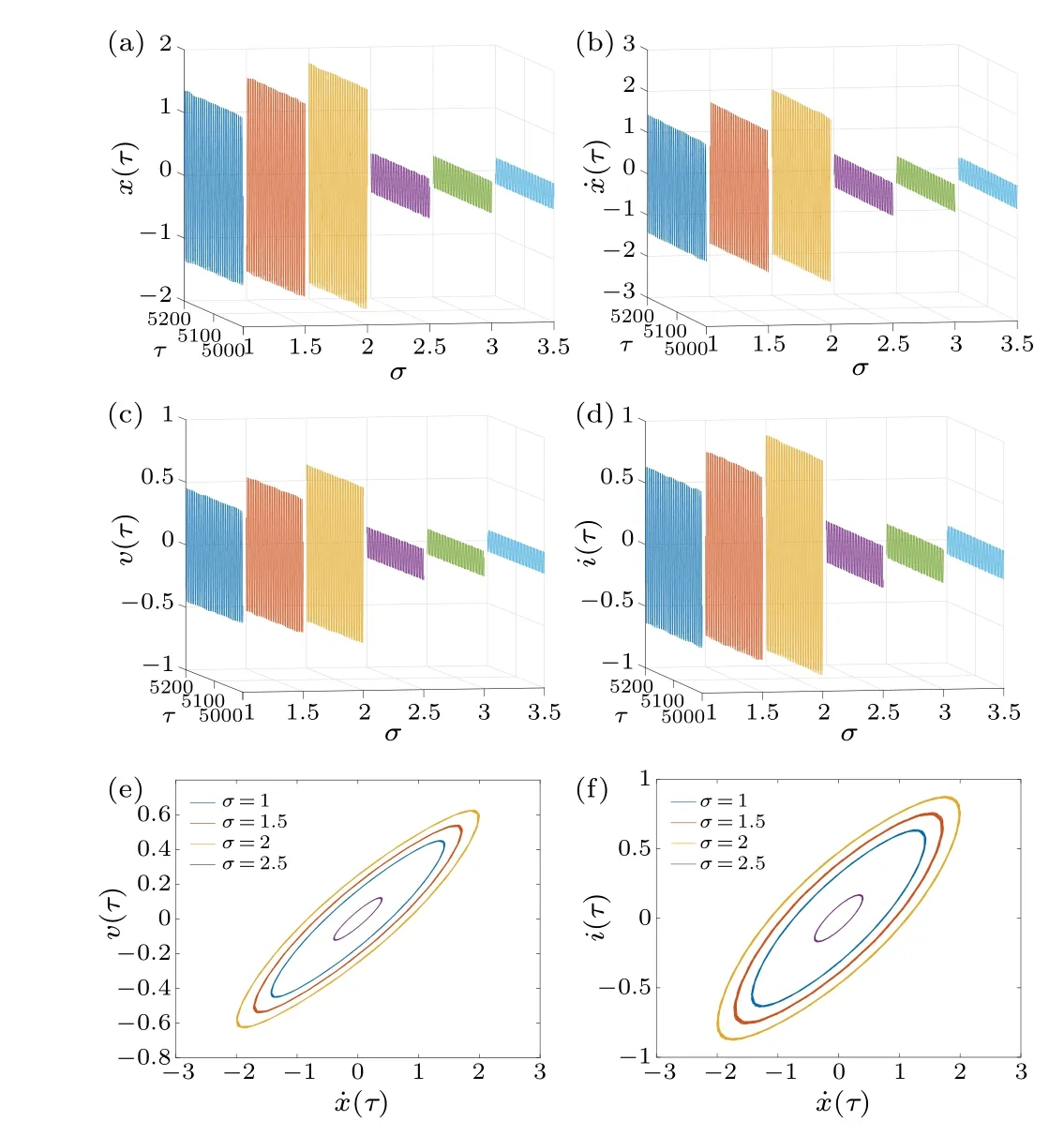
Fig.5.The stochastic response and phase plot under different frequencies σ for(a)–(f)γ =0.01.

Due to the existence of multiple coexisting attractors,the random components superimposed on the harmonic excitation will lead to different dynamic behaviors with different parameter values, which is called the stochastic bifurcation.[40,53]Figure 6 shows the bifurcation diagram about the steady-state momentE(a) underσandβ.The number of system solutionsE(a) is analyzed by employing the detuning frequencyσand viscoelastic parameterβas bifurcation parameters,and the corresponding bifurcation diagram is shown in Fig.7.The bifurcation diagram is divided into parts I and II, representing one solution and three solutions ofE(a),respectively.For a fixedβ, the number of the system solutionsE(a) changes from 1 to 3 and then from 3 to 1 with increasing the parameterσ,which verifies the stochastic jump phenomenon of the hybrid EHS in Fig.5.

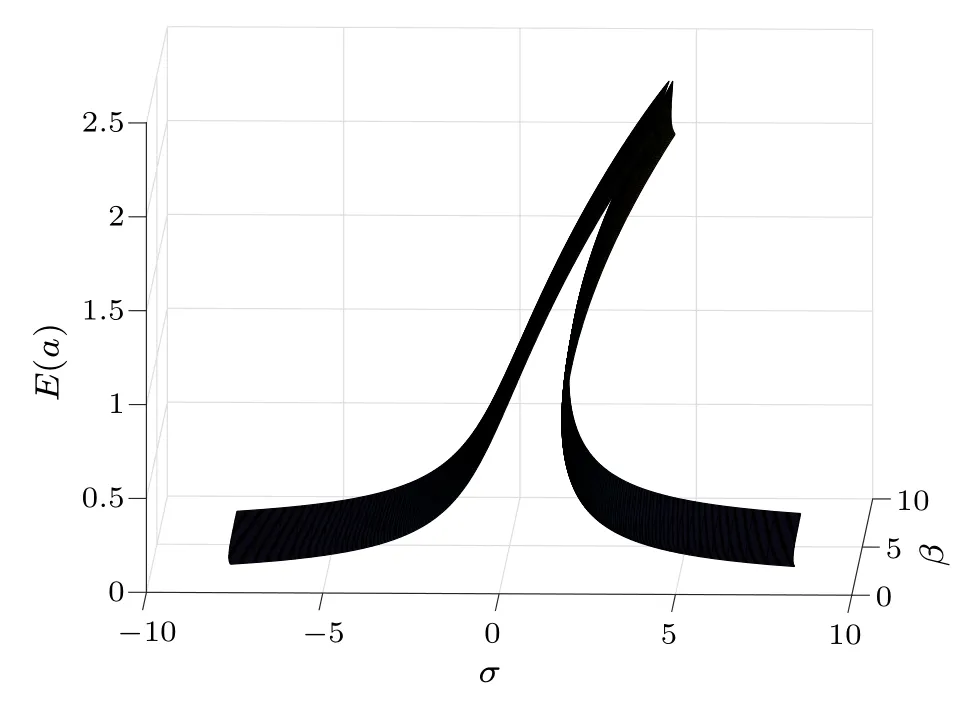
Fig.6.Bifurcation diagram of E(a)solutions versus σ and β.

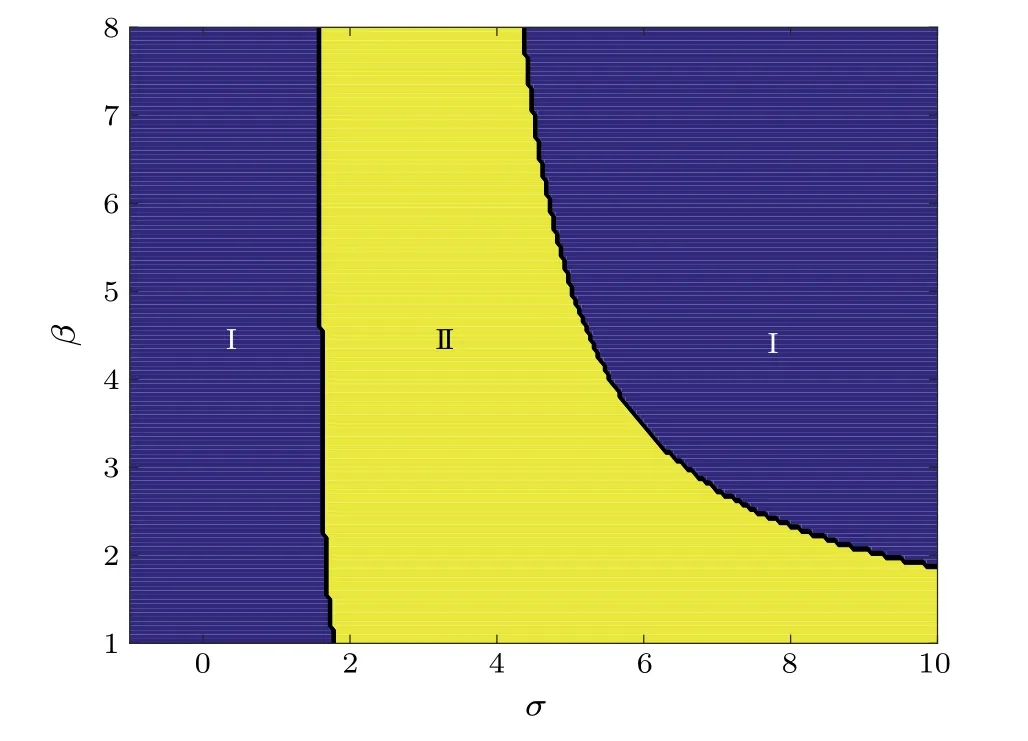
Fig.7.Bifurcation diagram of the number of E(a) solutions versus σ and β.

4.Efficiency analysis of energy harvesting

The mean-square electric voltageE(v2), mean-square electric currentE(i2), second-order steady-state momentE(a2), and mean output powerE(P) are indicators that can measure the efficiency of energy harvesting.In this section,we mainly pay attention to the changes ofE(v2),E(i2), andE(P)under different parameters.

Within a certain noise intensityγ,the effects of the electromechanical coupling coefficientq, the inverse of the product of the resistor and capacitorλ1and the viscoelastic parameterβonE(v2)are depicted in Figs.8(a),8(b),and 8(e),and the effects of the electromechanical coupling coefficientg,the ratio of resistance and inductanceλ2and the viscoelastic parameterβonE(i2)are shown in Figs.8(c),8(d),and 8(f),respectively.On the one hand,E(v2)decreases with increasing the parameterqorλ1in Figs.8(a)and 8(b),and similarlyE(i2)decreases with increasing the parametergorλ2in Figs.8(c)and 8(d).Figures 8(e)and 8(f)show thatE(v2)andE(i2)increase with the increase of the viscoelastic parameterβ.On the other hand,E(v2)andE(i2)increase with increasingγin Figs.8(a)–8(f).

Fig.8. E(v2) and E(i2) decreasing with increasing (a) q, (b) λ1, (c)g, and (d) λ2 for different γ (σ =1), while increasing with [(e), (f)]increasing β.

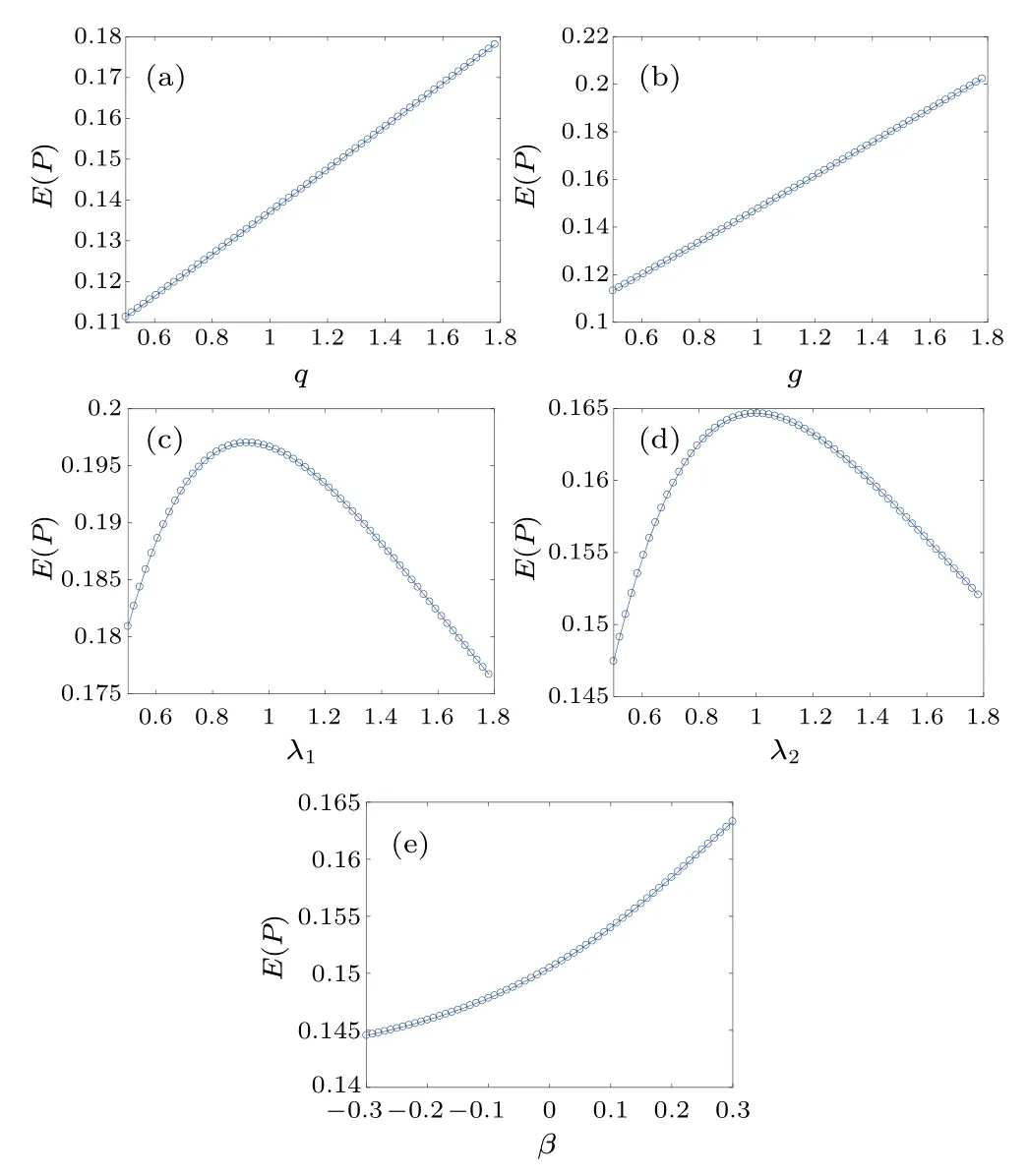
Fig.9.Evolution of E(P)versus q,g,λ1,λ2,and β for fixed γ =0.8,with(a)–(e)σ =1.

Figure 9 shows the effects of the parametersq,g,λ1,λ2,andβon the mean output powerE(P).E(P) increases with the increase ofq,gorβas shown in Figs.9(a),9(b),and 9(e),which reveal that system performance can be improved by increasing these parameters.However,E(P) firstly heightens and then reduces with the increase ofλ1orλ2in Figs.9(c)and 9(d).This indicates that there exist optimalλ1=0.941 andλ2=1.004 that maximize the mean output powerE(P)for fixedε=0.1,β=3,ω=1.5,F=1.6,β1=1,μ=2,q=1.2,g=1,λ1=3,λ2=2,σ=1, andγ=0.8, which can contribute to improvement of the energy harvesting performance.

Figures 10(a)and 10(b)depictE(a2)andE(P)increasing withβorγ.This suggests that a larger viscoelastic parameter or random excitation can improve the power output.

Figure 11 presents comparisons ofE(P)among the piezoelectric VEH, electromagnetic VEH, and hybrid VEH.It can be seen thatE(P)of the piezoelectric or electromagnetic VEH is lower than that of the hybrid VEH.This reveals that the hybrid EHS is more efficient at harvesting energy than the piezoelectric or electromagnetic EHS.

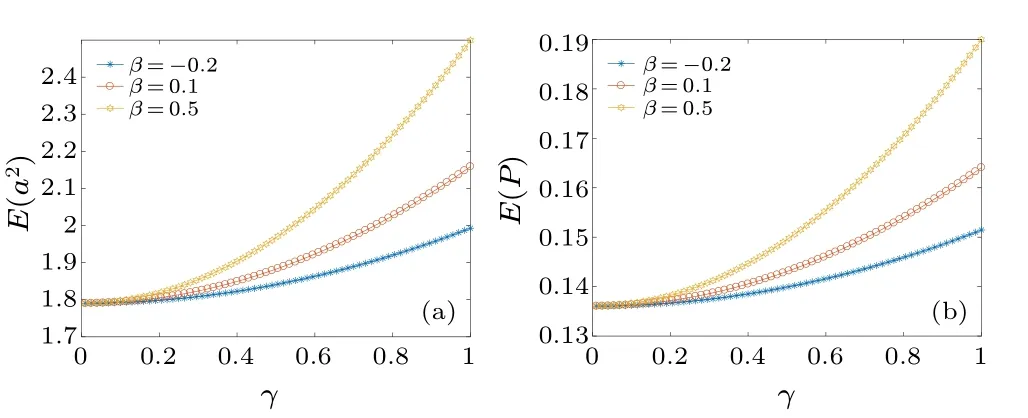
Fig.10.(a)E(a2)and(b)E(P)versus random excitation γ under different viscoelastic parameters β for σ =1.

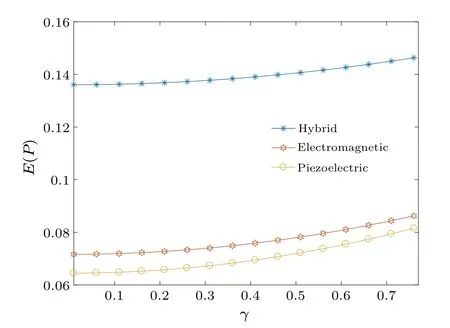
Fig.11.Comparisons of E(P)among hybrid harvester,electromagnetic harvester,and piezoelectric harvester(σ =1).

5.Conclusions

In summary, we have investigated the stochastic responses of the hybrid vibration EHS with a viscoelastic material under narrow-band noise, and revealed the influence of system parameters onE(v2),E(i2),andE(P).

The model of the hybrid VEH is briefly introduced, including the dimensionless system governing the equations derived by variable substitutions.Employing the multi-scales method, we obtain the first-order approximate solutions for the hybrid vibration EHS, and then derived the steady-state amplitude-frequency response formula and the FSSM for the amplitude.The numerical solutions obtained utilizing the Monte Carlo method are provided to verify the effectiveness of the method.The results show a good agreement between the numerical and approximate analytical solutions.Lastly,the effects of parametersq,g,γ,β,λ1,andλ2onE(v2),E(i2),andE(P)are discussed.

The main conclusions are provided as follows: (1) Enlarging the electromechanical coupling coefficientsqandgmakesE(v2)andE(i2)decrease but makesE(P)increase almost linearly.It is illustrated that increasing the electromechanical coupling coefficients can increase the efficiency of the hybrid EHS.(2)E(v2) andE(i2) increase with increasingλ1andλ2, butE(P) firstly increases and then decreases with increasingλ1andλ2,meaning that the optimal values ofλ1andλ2can be obtained to maximize the efficiency of energy harvesting.(3)E(v2),E(i2),andE(P)increase with the increases of the viscoelastic parameterβand the random excitationγ,suggesting that the increases ofβandγare beneficial to improving the efficiency of the hybrid EHS.

By comparing the piezoelectric EHS, electromagnetic EHS and hybrid EHS,it is found that the hybrid EHS has better energy harvesting efficiency than either the single electromagnetic EHS or the single piezoelectric EHS.

Acknowledgments

This work is supported by the National Natural Science Foundation of China (Grant Nos.12002089 and 11902081),the Science and Technology Projects in Guangzhou (Grant Nos.202201010326 and 2023A04J1323), and the Guangdong Basic and Applied Basic Research Foundation (Grant No.2023A1515010833).