Yarong Xia(夏亞榮), Kaikai Zhang(張開開), Ruoxia Yao(姚若俠), and Yali Shen(申亞麗)

1School of Information and Engineering,Xi’an University,Xi’an 710065,China

2School of Science,Xi’an University of Architecture and Technology,Xi’an 710055,China

3School of Computer Science,Shaanxi Normal University,Xi’an 710062,China

4Maths and Information Technology School,Yuncheng University,Yuncheng 044000,China

Keywords: Hirota bilinear method,long wave limit,hybrid solutions,trajectory equation

1.Introduction

Nonlinear partial differential equations (NLPDEs) play an important role in fluid mechanics, plasma, quantum field theory, and so on.[1-3]The exact solution of NLPDEs can describe various physical properties exhibited by the equation, therefore, the search for effective methods of solving NLPDEs has received a lot of attention.Until now,many useful methods have been proposed, such as Darboux transformation,[4,5]B¨acklund transformation,[7]inverse scattering transformation,[8]variable separation method,[9,10]Hirota bilinear method,[11-13]etc.Among them, Hirota bilinear method is most studied by many scholars owing to its simplicity and directness.In Refs.[14-19], the lump solutions to many NLPDEs were presented through Hirota bilinear method.Lump wave is a special rational function wave,which is localized in all directions of space.Manakovet al.gave the analytical expression of the lump solution when he studied the rational solution of the KP equation[20]firstly.In recent years, the interaction between lumps and solitons, breathers,rogue waves, etc.has become a research focus in the soliton theory.Liet al.investigated the high-order lumps,breathers,and hybrid solutions of the(2+1)-dimensional fifth-order KdV equation.[21]Wang constructed lump and interaction solutions to the(2+1)-dimensional Burgers equation in Ref.[22].Zhouet al.studiedn-lump and interaction solutions of localized waves to the (2+1)-dimensional generalized KDKK equation in Ref.[23].In Ref.[24], Zhanget al.provided the trajectory equation and phase expression of a lump before and after collisions with line and breather waves based on the hybrid solutions of the KP equation.In Ref.[25],Zhanget al.derived a new class of nonlinear superposition between lump waves and other waves of KPI equation.Xiaet al.discussed the trajectory equation of a lump before and after collisions withn-line andn-breather waves for (2+1)-dimensional Sawada-Kotera equation in Ref.[26].

In this paper, we will study the following (2+1)-dimensional GHSI equation

whereρi(i=1,..., 4) are arbitrary constants.Equation (1)is an important model in shallow water wave theory, which is proposed by Hirota and Satsuma via a B¨acklund transformation of the Boussinesq equation, it is an extension of the Hirota-Satsuma shallow water wave equation.In Refs.[27-31], the authors have studied Eq.(1) from different perspectives, mainly including multi-soliton solution, lump solution,breather solution, hybrid solutions, etc.However, there is no relevant research on the trajectory equation before and after the interactions of the GHSI equation with other nonlinear waves until now.This will be the main work of our paper.

The rest of this paper is organized as follows: In Section 2, then-soliton solution of Eq.(1) is constructed via the Hirota bilinear method.In Section 3, by employing the long wave limit method,the hybrid solutions consisting ofm-lump andn-soliton wave,m-lump, andn-breather wave for Eq.(1)are obtained.In Section 4, the trajectory equation and phase change of the lump wave before and after collisions withnsoliton andn-breather wave are given.The last section contains a discussion and summary.

2.The N-soliton solution for generalized Hirota-Satsuma-Ito equation

Through the dependent variable transformation

equation(1)can be converted into the following bilinear equation:

whereτ=τ(x,y,t),theDis the bilinear differential operator defined by

That is,ifτis a solution to Eq.(3),thenv=2(lnτ)xis a solution to Eq.(1).

Based on the Hirota bilinear method and transformation(2),then-soliton solution of Eq.(1)is

wherepi,qi,ωi, andφiare arbitrary constants, ∑μ=0,1represents the sum of all possible combinations ofμi=0,1 (i=1,...,N).

3.The M-lump solution and hybrid solutions for generalized Hirota-Satsuma-Ito equation

The long wave limit method is an effective method to construct lump solution for nonlinear differential equations.In this section, we will explore this method to the GHSI equation.

3.1.The M-lump solution for generalized Hirota-Satsuma-Ito equation

Taking the long wave limit for then-soliton solution(5)

we can get them-lump solution of Eq.(1)as

with

WhenN=2,M=1 for Eq.(6)and Eq.(7),the following 1-lump solution can be derived:

WhenN=4,M=2,the 2-lump solution of Eq.(1)is

3.2.Hybrid solutions for generalized Hirota-Satsuma-Ito equation

When we take the following partial long wave limit on Eq.(5),that is constraints

the hybrid solution betweenm-lump andn-soliton of Eq.(1)can be derived.

For example,whenm=1,n=1,

equation (12) denotes the hybrid solutions of 1-lump and 1-solitons,where

Whenm=1,n=2, we can yield the hybrid solutions of 1-lump and 2-solitons as

whereKijsatisfies Eq.(13).

Similarly,taking the following partial long wave limit onn-soliton solution(5):

the hybrid solutions betweenm-lump andn-breather wave of Eq.(1)can be obtained.

For example,whenm=1,n=1,the hybrid solutions of 1-lump and 1-breather are

It is easy to found that although equations (14) and (16)have the same expression form, they represent completely different hybrid solutions due to different constraints conditions(11)and(15).

4.Trajectory equation of a lump before and after collision with other waves for generalized Hirota-Satsuma-Ito equation

According to Eq.(7), the 1-lump solution of the (2+1)-dimensional GHSI equation can be expressed as

whereθiandKi jare given by Eq.(8).Through the extreme value theorem of binary functions,we can obtain the parameter equation of the wave peak and valley of the 1-lump solution for Eq.(1)as follows:

the parametric equations (18) and (19) can be converted into the following general form

From Eqs.(20)and(21),we know that the lump wave moves along a straight line,and the wave speed is

The height of peak and the depth of valley are respectively

It is well known that the research on the motion trajectory of the lump wave usually refers to study its peak motion.In order to better understand the motion behavior of the 1-lump wave, we select the parametersρ1=2,ρ2=2,ρ3=3,ρ4=3,P1=1+(3/4)I,P2=1-(3/4)I,Q1=-1/2+I,Q2=-(1/2)-I,the following image simulations are shown in Fig.1.

4.1.Trajectory equation of 1-lump before and after collisions with n-soliton

In this subsection, with the help of the motion trajectory of a single lump, we mainly study the trajectory equation of 1-lump before and after collisions withn-soliton.In order to give a concise form of the trajectory equation before and after collisions,we refer to the following two function tokens:

4.1.1.Trajectory equation of 1-lump before and after collisions with 1-soliton

To proceed,with the help of expression(12),we propose the trajectory equation of 1-lump before and after collisions with 1-soliton for Eq.(1)by Theorem 1,and the related proof is given.

Theorem 1 If the hybrid solution between 1-lump and 1-soliton for Eq.(1)can be represented as Eq.(12),and

then, before and after the collisions of 1-lump and 1-soliton,the trajectory equations for the lump wave are

with

the phase change of the lump wave is

However,before and after the collisions,the height and depth of the lump wave do not change,they still satisfy Eqs.(23)and(24).Where sign(x)is a symbolic function,x-,y-andx+,y+are the trajectory equations of the lump wave before and after collisions with solitons respectively.

Proof Applying the following constraints:

to the second equation of Eq.(12),it can be transformed into

where

For Eq.(31),we first discuss the case ofλ3＞0.

Whenλ3＞0 andt →-∞,equation(31)can be reduced to the following form:

Whent →∞,due to the invariance of the solutionv=2(lnτ)x,we multiply the expression exp(-λ3t-η3)to the right side of Eq.(31)will get

Solving Eq.(30),c1andc2can be obtained below:

Substituting Eq.(35)into Eqs.(33)and(34)leads to

Here,bothτ-andτ+satisfy the bilinear equation(3).Therefore,before and after collisions,the trajectory equations of the lump wave can be written as

The general forms of Eq.(37)are

Substitutingx-,y-andx+,y+into the solutionv=2(lnτ)x,it can be verified that the height and depth of the lump wave remain unchanged.For the case ofλ3＜0, the proof process is similar to the case ofλ3＞0,it is omitted here.

From Theorem 1, we find that the collision between 1-lump and 1-soliton is elastic whenλ3/=0.In order to better characterize Theorem 1, let the parametersρ1=2,ρ2=2,ρ3=3,ρ4=3,P1=-1/2,P2=-1/2,Q1=I,Q2=-I,p3=1/3,q3=-5/6,φ3=0, the corresponding diagrams plotted in Fig.2.

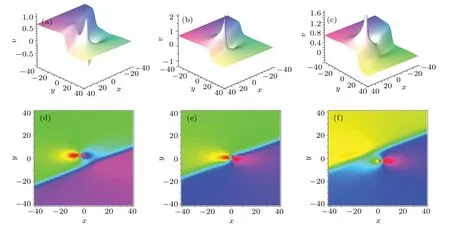
Fig.2.Evolution behaviors of hybrid solution of 1-lump and 1-soliton for Eq.(1)at t=-10,0,10:(a)-(c)three-dimensional(3D)plots;(d)-(f)density plots.

4.1.2.Trajectory equation of 1-lump before and after collisions with 2-soliton

In this part,the trajectory equation of 1-lump before and after the collisions with 2-soliton is discussed from the 4-soliton solution,and the trajectory equation of 1-lump colliding withn-soliton is given.

Theorem 2 If the hybrid solution between 1-lump and 2-solitons for Eq.(1)can be represented as Eq.(14),and

then,before and after collisions,the trajectory equations of the lump wave are given below:

whereβiandγiare determined by Eq.(28).Before and after collisions,the phase change of the lump is

But the height and depth of the lump do not change and are consistent with Eqs.(23)and(24).

Proof By employing the condition(30),the second equation of Eq.(14)can be converted into

whereχiandηisatisfy Eq.(32).

For Eq.(42), we need to consider the following casesλ3＞0,λ4＞0;λ3＞0,λ4＜0;λ3＜0,λ4＞0, andλ3＜0,λ4＜0.Here,we only discuss the first two cases,and the others can be discussed in the same way.

(i)Whenλ3＞0,λ4＞0,according to the method in Theorem 1,whent →-∞andt →∞,equation(42)can be written as

the trajectory equations of the lump wave before and after collisions are given below:

The general forms of Eq.(44)are as follows:

By Eq.(45), we can yield the value of phase change in Eq.(41).Substituting Eq.(44) intov=2(lnτ)x, the height and depth of the lump wave do not change.

(ii)Whenλ3＞0,λ4＜0,we have

The general equations corresponding to Eq.(47)are

The values of Eq.(41)of the phase change can be obtained by Eq.(48).Substituting Eq.(47)intov=2(lnτ)x,we can verify that the height and depth of the lump wave do not change.

To better explain the Theorem 2, by taking a set of parametersρ1=2,ρ2=2,ρ3=3,ρ4=3,P1=I/2,P2=-I/2,Q1=1+I/4,Q2=1-I/4,p3=1/4,p4=1/7,q3=-3/4,q4=-2,φ3=0,φ4=0, the collision diagrams of a lump wave and two-kink soliton can be given in Fig.3.

By further generalizing Theorem 1 and Theorem 2, the trajectory equations before and after collisions of 1-lump andn-solitons can be obtained below.

Theorem 3 Ifλi/=0, (i=3, 4,..., 2+n), then before and after 1-lump wave collidings withn-solitons, the trajectory equations of the lump wave are as follows:

The phase shift of lump wave is

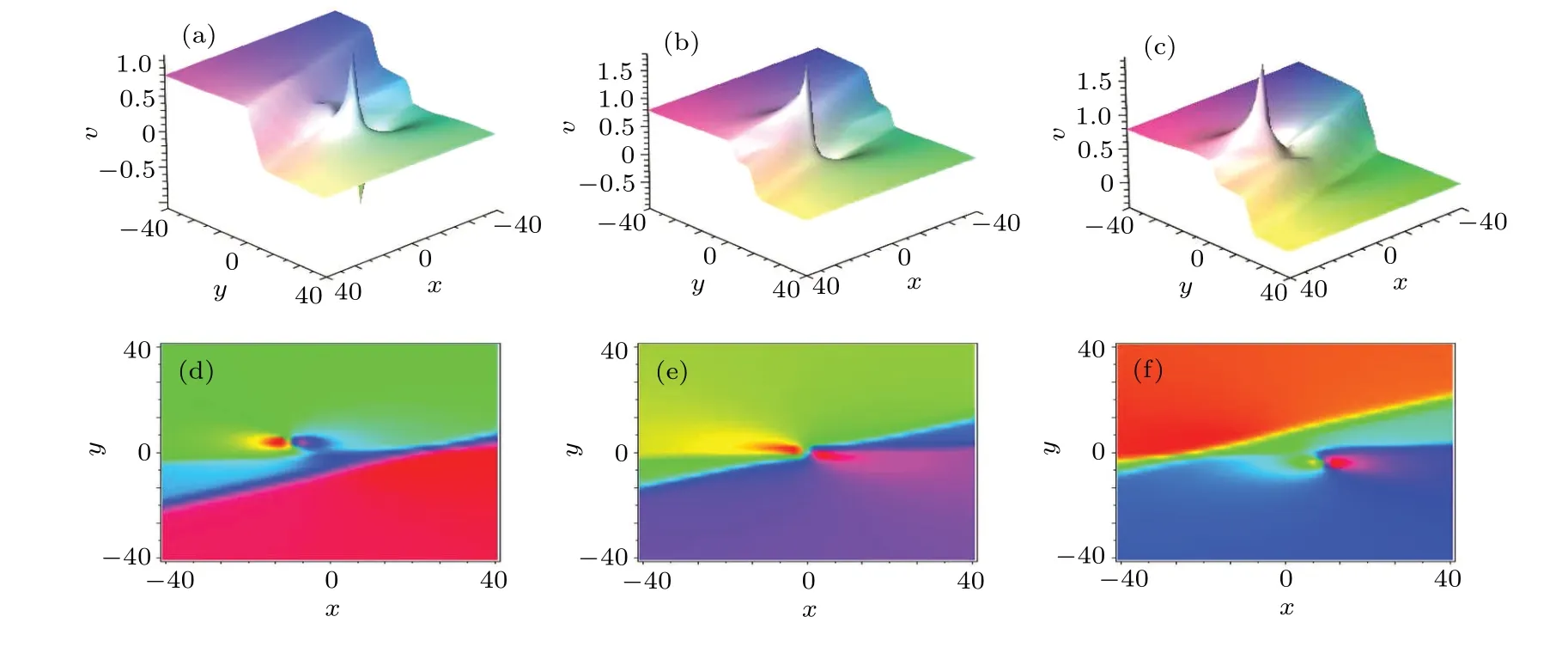
Fig.3.Evolution behaviors of hybrid solution of 1-lump and 2-soliton for Eq.(1)at t=-30,0,30: (a)-(c)the 3D plots;(d)-(f)density plots.

4.2.Trajectory equation of 1-lump before and after collisions with n-breather

In this subsection, the motion trajectories and phase expressions of the lump wave in the hybrid solutions of 1-lump and 1-breather,1-lump andn-breather will be investigated.

Theorem 4 If ?(λ3), ?(λ4)/= 0, then the trajectory equations of the collisions between 1-lump and 1-breather are

and the phase shift of the lump wave is

Comparing Theorem 2 and Theorem 4,their proof procedures are similar except for different constraint conditions, so the proof process will not be given here.In order to better describe the motion trajectory of 1-lump and 1-breather before and after collisions,the collision diagrams can be given in Fig.4 by selecting parametersρ1=2,ρ2=2,ρ3=3,ρ4=3,P1=3+I,P2= 3-I,Q1= 1+6I,Q2= 1-6I,p3= 3I,p4=-3I,q3=5/2,q4=5/2,φ3=0,φ4=0.

Next,we further extend Theorem 4 to the case of 1-lump collidings withn-breather.The specific content is shown in the following Theorem 5.

Theorem 5 If ?(λi)/=0,(i=3,4,...,2+2n),then, before and after collisions of a lump andn-breather the trajectory equations of the lump wave are

and the phase shift of the lump wave is

5.Summary and discussion

In this paper, the trajectory equations of a lump before and after collisions with other waves for generalized Hirota-Satsuma-Ito equation are studied.Firstly, we start from the multi-soliton solution of the (2+1)-dimensional GHSI equation, many different types of mixed solutions of the GHSI equation are derived,such as the interaction between the lump solution and the line-soliton solution, the lump solution, and the breather solution.Secondly, under the constraint conditionsλi/=0, ?(λi)/=0 the trajectory equations of the lump wave before and after collisions withn-soliton(Theorm 3)andn-breather(Theorm 5)are proposed,and we have proved that the collision between lump and other waves are elastic,and the height and depth of the lump wave do not change.However,what does it mean whenλi=0,?(λi)=0? It will be shown in our subsequent research.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant Nos.12001424 and 12271324), the Natural Science Basic Research Program of Shaanxi Province,China (Grant No.2021JZ-21), the Chinese Post Doctoral Science Foundation (Grant No.2020M673332), and the Three-year Action Plan Project of Xi’an University (Grant No.2021XDJH01).