High-order effect on the transmission of two optical solitons
Houhui Yi(伊厚會(huì)), Yanli Yao(姚延立), Xin Zhang(張?chǎng)?, and Guoli Ma(馬國(guó)利),?
1School of Intelligent Manufacturing,Weifang University of Science and Technology,Weifang 262700,China
2Institute of Aeronautical Engineering,Binzhou University,Binzhou 256603,China
Keywords: nonlinear optics,optical communication system,optical solitons,solitons interaction
1.Introduction
The transmission characteristics of solitons in optical fibers have always been a hot research direction.[1-4]Due to the balance between dispersion and nonlinear effects, optical pulses can be transmitted in soliton form without distortion in the anomalous dispersion region of the optical fiber.[5,6]In this case, the nonlinear Schr¨odinger (NLS) equation is generally used as the mathematical model,which can be used to describe the transmission of optical pulses in the fiber, and the mathematical model only includes group velocity dispersion and self-phase modulation effects.[7-12]However, with the development of ultrashort pulse technology, when the pulse width of solitons is in the order of subpicosecond or femtosecond,the higher-order nonlinear effect and higher-order dispersion effect of optical fibers have a greater impact on solitons.[13,14]At this time, the transmission equation needs to be modified to the higher-order NLS equation.[15,16]Therefore, all kinds of NLS equations are the nonlinear dynamic basis for studying the propagation characteristics of solitons.[17,18]Among them, this type of equation has a first-order soliton solution in hyperbolic secant form,which maintains its shape and frequency spectrum unchanged during transmission.When the input energy of solitons is large,they will evolve into higherorder solitons, which in turn will involve the interaction between solitons.[19-22]
The interaction of solitons to some extent can affect the transmission quality of optical communication.So as to achieve distortionless transmission of ultra-short pulses and truly meet the requirements of high bandwidth and high transmission capacity,overcoming the influence of high-order dispersion and nonlinear effects has become a hot research topic.[23-25]In addition, in fiber optical communication, reducing the distance between adjacent solitons can increase the bit rate, but the interaction between solitons is more severe during this time.Therefore,it is necessary to study its action law and propose suppression methods to improve communication quality.[26-29]
In this article, based on the higher-order NLS equation,the transmission characteristics of femtosecond solitons in fibers and the interaction between them are analyzed and studied.The intuitive transmission form and interaction law of femtosecond solitons in fibers are obtained when considering different higher-order effects.The specific form of this transfer equation is shown as[30]
For Eq.(1), the modulation instability has been analysed.[30]However, the soliton interactions have not been reported before.We will discuss the influences of the higher-order effects on their interactions to optimize the transmission characteristics of optical solitons in optical communication systems.
In this paper, the bilinear form and the two soliton solutions of the equation are obtained.Then, the two soliton solutions are analyzed and the evolution characteristics of the two solitons under various conditions are studied.Finally, a summary is provided for this article.
2.Two-soliton solutions
For Eq.(1), we first assume thatu(x,t)=h(x,t)/f(x,t),and the forms ofh(x,t)andf(x,t)can be written as
By substituting the assumed form ofu(x,t) into Eq.(1),we can obtain the bilinear forms of it as
with the coefficient constraint relationship beingα=γ2/(3γ1).Assuming that
among them,
Substituting them into Eq.(3),we can get that
For Eq.(2),we assume that
and then can obtain the coefficients as
Thus,we setε=1,and the two-soliton solutions can be presented as
3.Discussion
For solutions(10), we assumek11=1,k12=0,k21=2,k22=0,ξ11=1,ξ12=0,ξ21=3,ξ22=0,A1=1,andA2=2.At this point,we can obtain various cases of two soliton interactions when we take different values ofγ1andγ2, as shown in Fig.1.Whenγ1=-0.53 andγ2=-1.9,we find that two optical solitons interact nearx=0.During the interaction process,two optical solitons will be fused into one optical soliton,and the energy of this optical soliton will increase sharply.After the interaction,both optical solitons will undergo the phase shift and propagate along their original velocity and amplitude.By changing the values ofγ1andγ2,we can change the incident phase, propagation speed, and amplitude of optical solitons as shown in Figs.1(b)-1(d).It should be emphasized that as the values ofγ1andγ2increase in Fig.1(d),the amplitude of optical solitons will significantly increase, and unstable phenomena may occur during the transmission due to high energy.
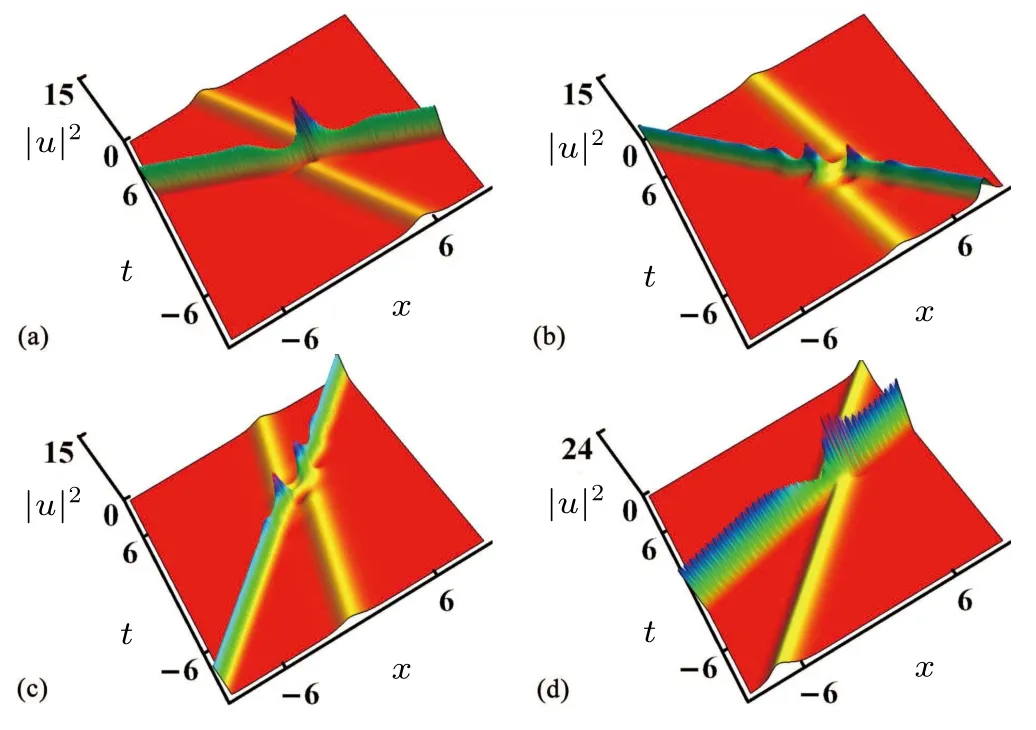
Fig.1.The influence of γ1 and γ2 on two-soliton transmission.Parameters are k11 =1, k12 =0, k21 =2, k22 =0, ξ11 =1, ξ12 =0, ξ21 =3,ξ22=0,A1=1,A2=2 with(a)γ1=-0.53,γ2=-1.9;(b)γ1=-0.22,γ2=-1.3;(c)γ1=0.25,γ2=1.3;(d)γ1=1,γ2=1.4.
Based on the values of Fig.1(c),we discuss how different values ofk11,k12,k21andk22affect the interaction of optical solitons.Unlike Fig.1(c),in Fig.2(a),the incident phase and amplitude of the optical soliton have changed whenk11,k12,k21andk22take different values.By changing the values ofk11,k12,k21andk22, we further change the interaction state of optical solitons.In Fig.2(c),when the small amplitude optical soliton interacts with the large amplitude optical soliton,the modulation will occur at the interaction point,making the optical soliton transmission unstable.In Fig.2(d),two optical solitons achieve parallel transmission, and even if their spacing is small,no interaction occurs.
In Fig.3, based on the relevant parameter values in Fig.2(b), we only change the values ofξ11,ξ12,ξ21andξ22,and discuss their impact on the interaction of optical solitons.From Fig.3,we can see that changing the values of them only has a certain impact on the phase of the optical solitons, and does not affect the overall transmission state of the optical solitons.Based on Fig.3(d),we simultaneously change the values ofk11,k21,γ1andγ2,and find that the interaction state of optical solitons has undergone a significant change.During the interaction process,optical solitons will oscillate.The severity of oscillation during interaction can be effectively controlled through those parameters.The closer the values ofγ1andγ2are, the more intense their interaction is and the longer their interaction time is.
In Fig.5,we mainly discuss the impact of changes ink11,k21,γ1andγ2on the interactions of optical solitons.We find that the interaction characteristics of optical solitons have not undergone fundamental changes.Their initial incident phase only has some small changes, but their intensity varies during the interaction,and the amplitude of optical solitons varies greatly.
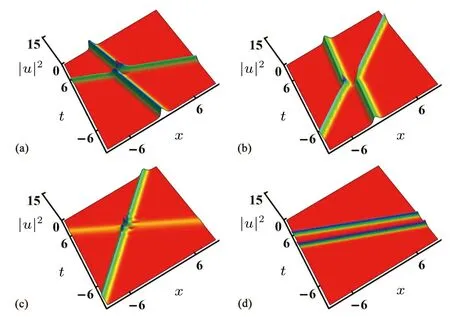
Fig.2.The influence of k11, k12, k21 and k22 on two-soliton transmission.Parameters are ξ11 = 1, ξ12 = 0, ξ21 = 3, ξ22 = 0, A1 = 1,A2 = 2, γ1 = -0.22, γ2 = -1.3 with (a) k11 = -1.7, k12 = -0.97,k21=2,k22=0.28;(b)k11=-1.7,k12=0.34,k21=-1.9,k22=0.81;(c) k11 = -0.75, k12 = -1.9, k21 = 1.5, k22 = 0.59; (d) k11 = -1.6,k12=-1.4,k21=-1.4,k22=-1.5.
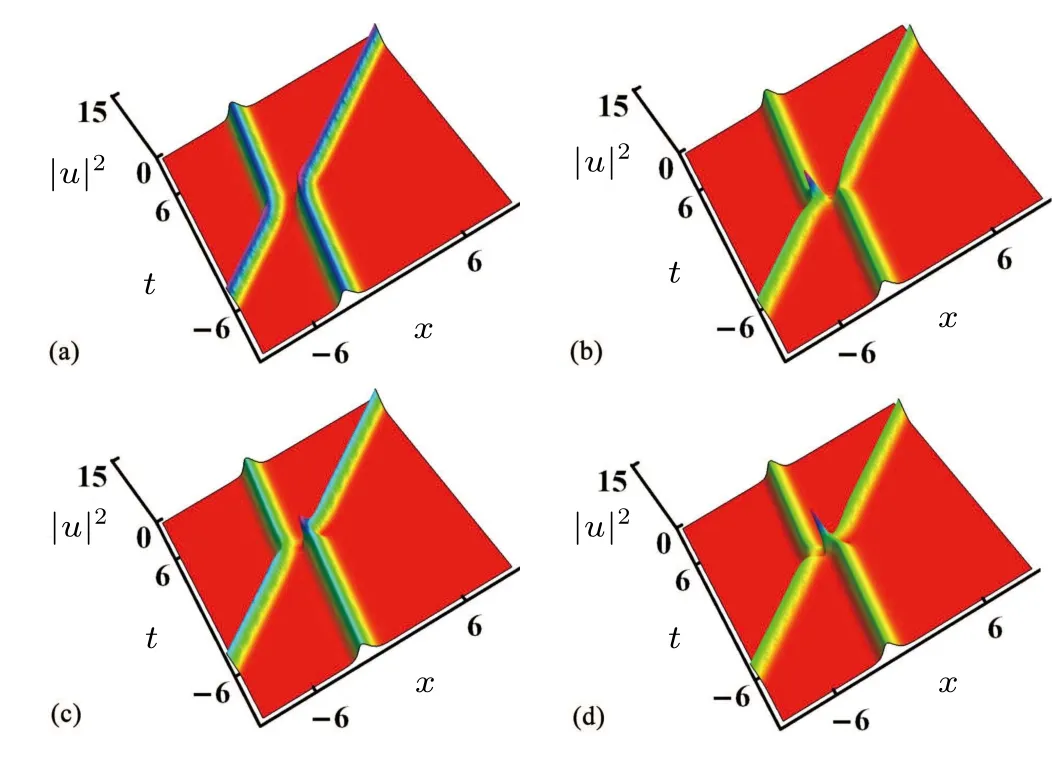
Fig.3.The influence of ξ11,ξ12,ξ21 and ξ22 on two-soliton transmission.Parameters are k11=-1.7,k12=0.34,k21=-1.9,k22=0.81, A1 =1, A2 =2, γ1 =-0.22, γ2 =-1.3 with (a) ξ11 =-2,ξ12 =-1.8, ξ21 =-2, ξ22 =0.8; (b) ξ11 =-0.41, ξ12 =-0.63,ξ21 = 0.88, ξ22 = -0.91; (c) ξ11 = 0.34, ξ12 = 0, ξ21 = -1.8,ξ22=1.7;(d)ξ11=1,ξ12=1.5,ξ21=-0.16,ξ22=-1.9.
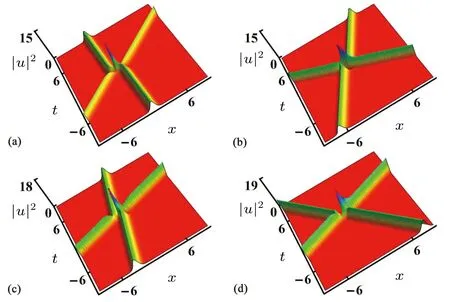
Fig.5.The influence of k12, k22, γ1 and γ2 on two-soliton transmission.Parameters are k11=-1.7,k21=-1.9,ξ11=1,ξ12=1.5,ξ21=-0.16,ξ22=-1.9,A1=1,A2=2 with(a)k12=0.84,k22=0.41,γ1=-0.28,γ2 =-1.3; (b) k12 =-2, k22 =-0.38, γ1 =-0.5, γ2 =-2; (c) k12 =0.38, k22 =1.4, γ1 =-0.2, γ2 =-0.56; (d) k12 =-0.78, k22 =0.28,γ1=0.63,γ2=1.6.
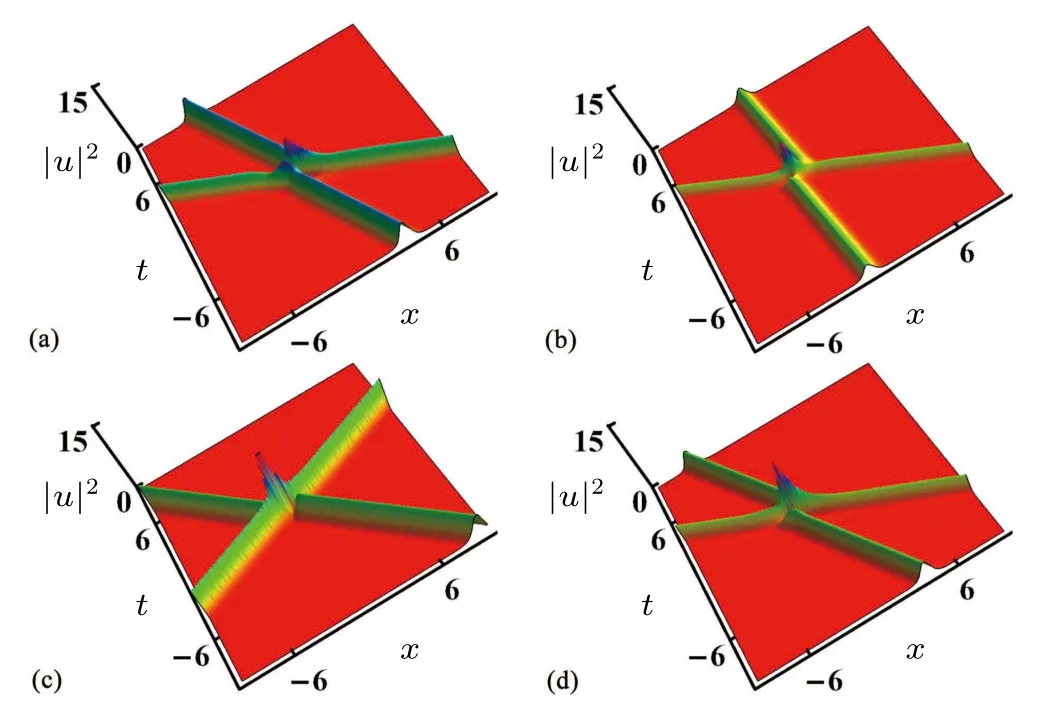
Fig.6.The influence of ξ11, ξ21, γ1 and γ2 on two-soliton transmission.Parameters are k11 = -1.7, k12 = -0.78, k21 = -1.9,k22 =0.28, ξ12 =1.5, ξ22 =-1.9, A1 =1, A2 =2 with(a)ξ11 =0,ξ21 = 0.44, γ1 = -0.31, γ2 = -1.4; (b) ξ11 = 1.3, ξ21 = -0.84,γ1=-0.2,γ2=-1.6;(c)ξ11=0.44,ξ21=1.2,γ1=0.53,γ2=1.8;(d)ξ11=0.53,ξ21=-0.81,γ1=-0.34,γ2=-1.9.
In Fig.6,we discuss how the values ofξ11,ξ21,γ1andγ2change the transmission characteristics of two optical solitons.We find that the interaction characteristics of optical solitons are similar to those in Fig.5, except that the intensity of the interaction varies at different initial incident phases.In Fig.7,the values ofξ12,ξ22,γ1andγ2are changed,and the interaction characteristics of optical solitons are different from those in Fig.6.Two optical solitons exhibit repulsive properties at the interaction point in Figs.7(b)and 7(c).Thus,we can find thatγ1andγ2can influence the soliton incident phase,propagation speed and amplitude.k11,k12,k21andk22can change the interaction state,and the modulation and parallel transmission can occur.ξ11,ξ12,ξ21andξ22have a certain impact on the soliton phases, and do not affect the overall soliton transmission state.
4.Conclusion
The research work in this paper mainly bases on the highorder NLS Eq.(1).By solving the equation analytically, the transmission characteristics of a single femtosecond soliton in the optical fiber and the interaction of two optical solitons have been studied under the condition of considering various highorder effects.The transmission characteristics and laws of their interactions in optical fibers have been analytically studied under different initial inputs and different high-order effects.The changes in the values ofγ1andγ2have a significant impact on the interaction of optical solitons,leading to significant changes in the phase, velocity, and amplitude of optical solitons.At the same time, at the interaction point, different initial values and different higher-order effects have led to different degrees of interaction, and have also led to attraction and repulsion at the interaction point.The conclusion of this paper will provide a theoretical reference for further obtaining ultra-short and ultra-high energy optical solitons.
Acknowledgments
Project supported by the Scientific Research Foundation of Weifang University of Science and Technology (Grant No.KJRC2022002), the Shandong Province Higher Educational Science and Technology Program (Grant No.J18KB108), and the Research start-up fees for doctoral degree holders and senior professional title holders with master’s degrees of Binzhou University(Grant No.2022Y12).
- Chinese Physics B的其它文章
- Corrigendum to“Reactive oxygen species in plasma against E.coli cells survival rate”
- Dynamic decision and its complex dynamics analysis of low-carbon supply chain considering risk-aversion under carbon tax policy
- Fully relativistic many-body perturbation energies,transition properties,and lifetimes of lithium-like iron Fe XXIV
- Measurement of the relative neutron sensitivity curve of a LaBr3(Ce)scintillator based on the CSNS Back-n white neutron source
- Kinesin-microtubule interaction reveals the mechanism of kinesin-1 for discriminating the binding site on microtubule
- Multilevel optoelectronic hybrid memory based on N-doped Ge2Sb2Te5 film with low resistance drift and ultrafast speed

