Wei-Tao Lu(盧偉濤), Yue Mao(毛岳), and Qing-Feng Sun(孫慶豐),3,?

1School of Sciences,Nantong University,Nantong 226019,China

2International Center for Quantum Materials,School of Physics,Peking University,Beijing 100871,China

3Hefei National Laboratory,Hefei 230088,China

Keywords: valleytronics,equal-spin Andreev reflection,spin-triplet Cooper pairs,Ising superconductor junction

1.Introduction

Recently, valleytronics have attracted much attention in two-dimensional layered materials such as graphene and transition metal dichalcogenides(TMDs).[1-3]Analogous to spintronics, valleytronics aim to generate, control, and detect the valley degree of freedom,which have potential applications in semiconductor technologies and quantum information.Many topics of valleytronics have been reported in recent years,including valley-polarized transport,[4]quantum valley Hall effect,[5-7]spin-valley locked physics,[8,9]chiral optical selection rules,[10]etc.Because of the Berry phase difference for the two valleys induced by magnetic field, the giant valley splitting and unusual valley crossing are observed in the graphene resonators.[10]The strong spin-orbit coupling(SOC)and broken inversion symmetry of TMDs give rise to a valleydependent optical selection rule, where the right (left) circularly polarized light couples to interband transitions in theK(K＇)valley.[9]The transition from valley-Hall phase to anomalous Hall phase and the valley-Hall conductivity switch could occur in graphene WSe2heterostructures under off-resonant polarized light.[11]

Andreev reflection (AR) is a process of electron-hole conversion that occurs at the interface of a normal metal(N)and superconductor(SC).[12]The incident electron in the metal is reflected at the N/SC interface as a hole,and a Cooper pair is injected into the SC.Generally,the state of Cooper pair is spin singlet.Considering the spin and valley degrees of freedom, the Cooper pair is composed of electrons from the opposite spins in opposite valleys.[13-20]Thus, it is possible to detect the valley polarization of edge states by the AR.[13]The two electrons of a Cooper pair tunneling into SC could move in opposite directions in the bilayer graphene because they belong to different valleys and the valley-chiral modes are formed at the domain walls.[16]The spin-valley switch effect can be realized between the crossed AR and the elastic cotunneling by adjusting the electric field in the antiferromagnet/SC junctions.[17]

Due to the broken inversion symmetry of TMDs,the spin splitting is opposite at the two valleys and is pinned to the out-of-plane direction, so the SOC of TMDs is termed Ising SOC.[1,2]Recent experimental works reveal that the superconductivity could be realized in various TMDs.[21-25]With the application of gate voltage,MoS2thin films could exhibit electric field-induced superconductivity with a critical temperature 10 K.[21]Due to the Ising SOC in TMDs such as MoS2and NbSe2, the in-plane upper critical field of the superconductor is enhanced remarkably,which exceeds the Pauli paramagnetic limit by several times.[22,23]Hence, the so-called Ising SC (ISC) provides an opportunity to study the superconducting spintronics.Interestingly, the Ising SOC generates equal-spin triplet Cooper pairs in ISC and results in a topological superconductor with Majorana zero modes.[26,27]ISC can induce a robust topological superconducting gap in InSb nanowires with a strongly enlarged topological regime due to the equal-spin Cooper pairs.[28]The spin-singlet and spin-triplet pairing correlations could be manipulated by applying an in-plane magnetic field to the ISC.[29,30]In particular, the spin-triplet AR is investigated in the conductor/ISC hybrid junctions.[31-35]The equal-spin AR in ferromagnet/ISC junctions shows a strong magnetoanisotropy with periodπ, which can be enhanced by single-band ISC.[31]The equal-spin AR gives rise to the switch effect of spintriplet Josephson current and 0-πtransitions in ISC Josephson junctions.[32]The equal-spin crossed AR could take place in a ferromagnet/ISC/ferromagnet junction due to the spin-triplet Cooper pairs, and it has a significant increase for half-metal ferromagnet.[34]Furthermore, the spin transport through the N/ISC junction demonstrates that ISCs also have the characteristic of spin superconductivity.[33,35]Even so,the influence of valley degree of freedom on equal-spin AR in the ISC junction still needs to be explored.

In this paper,we theoretically investigate the property of equal-spin AR in the ferromagnet/ISC(FM/ISC)junction with a circularly polarized light applied to the FM, as shown in Fig.1(a).It is found that although the Cooper pair is valleysinglet state in the ISC, the AR is sensitive to the valley degree of freedom due to the optical irradiation.The valleydependent equal-spin AR and normal AR happen in different regions and exhibit different behaviors.The irradiation of light destroys the symmetry of valley-dependent AR, leading to a strong magnetoanisotropy of AR with period 2π.The equalspin-triplet Cooper pairs could give rise to a valley-dependent spin supercurrent in the ISC.The results can be understood in terms of half-metal phase, Ising superconducting phase, and the symmetry of the system.

The rest of the paper is organized as follows.In Section 2,we give the Hamiltonian of the light-irradiated FM/ISC junction and the formula for AR.The results on valley-dependent equal-spin AR and spin transport are discussed in Section 3.Finally,a summary is presented in Section 4.

2.Theoretical model and formula

We mainly study the character of equal-spin AR under the application of light, which is a powerful method to regulate electronic properties.Many intriguing phenomena are found in the optically driven nonequilibrium systems, such as light-induced superconductivity,[36,37]photoinitiated insulator-metal transition,[38]Floquet topological phases,[39,40]and light-induced anomalous Hall effect.[41]For the circularly polarized light irradiated onto the TMDs sheet,the corresponding electromagnetic potential may be represented byA(t)=A(±sin(Ωt),cos(Ωt)), where the signs±refer to the right/left circular polarization,Ωis the frequency of the light, andA=E0/ΩwithE0being the amplitude of the electric fieldE(t)=?A(t)/?t.The gauge potential satisfies time periodicityA(t+T)=A(t)withT=2π/Ω.When the light frequency is off resonant for any electron transitions(ˉhΩ ?tjwith the hopping energytj), the effect of such an off-resonant light can be described by a static effective Hamiltonian.Based on the Floquet theory,[42]the static Hamiltonian near the valleys has the formηλv,where the valley indexη=±is for theKandK＇valleys.λv=(eAvF)2/ˉhΩis the effective energy describing the effects of the off-resonant circularly polarized light,which is positive(negative)for the right(left)circularly polarized light.In contrast with the on-resonant optical induction which can cause the photon-assisted tunneling and photon-assisted AR due to the photon absorption/emission,[43]the off-resonant light cannot generate real photon absorption/emission but can lead to the valley-dependent band structure and valley-dependent equal-spin AR.Furthermore, the off-resonant light could also induce various topological phases such as quantum spin Hall effect and quantum valley Hall effect.[11,44,45]

The low-energy electronic properties of TMDs may be well described by a minimal band model.[9,26]Considering the magnetization vector and the off-resonant circularly polarized light, the electronic states of TMDs in the vicinity of the valleys can be approximately expressed by the two-bandk·pHamiltonian[26]

Here,kdenotes the wave vector relative to the valleysKandK＇.σ= (σx,σy,σz) is the Pauli matrix of the spin space,λsis the Ising SOC strength, andμis the chemical potential.Remarkably, the lightλvcould lift the valley degeneracy.M=M(sinθcosφ,sinθsinφ,cosθ) is the magnetization vector with the exchange energyM, the polar angleθ,and the azimuthal angleφ, which could lift the spin degeneracy and break the time-reversal symmetry.Ising SOCλshas opposite directions in opposite valleys and could induce spin-triplet pairing correlations in the in-plane directions.[26]For the FM/ISC junction,we set chemical potentialμ=μISCin the ISC region andμ=μFMin the FM region.The Ising SOC strengthλsis assumed to be zero in the FM region.The light and the magnetization are only applied to the FM region[see Fig.1(a)], where the valley degeneracy and spin degeneracy are lifted.In the ISC region, only the Ising SOC exists and there is no light field and magnetization withλv=M=0.Therefore, the time-reversal symmetry still holds in the ISC region.

The Bogoliubov-de Gennes Hamiltonians for the FM/ISC junction can be written as

where ˉη=-ηand ?Δ=Δeiφiσyis the s-wave superconducting order parameter with the superconducting gapΔ.The HamiltonianHη(k)describes electron excitations with certain spin at certain valley, while-H?ˉη(-k) describes hole excitations with opposite spin at opposite valley.The superconducting gapΔcouples the time-reversed electron and hole states from opposite spins and opposite valleys.The dispersion relations of the FM region and ISC region can be described as

where±are for the particles with spin up and spin down,respectively.From Eqs.(3)and(4)one may find that it is halfmetal phase atμFM＜min(M+λv,M-λv) and metal phase atμFM＞min(M+λv,M-λv)in the FM region.Equation(5)implies that the phase of ISC is single-band atμISC＜λsand double-band atμISC＞λs.The half-metal phase and Ising superconducting phase play a key role in the AR process.

For an incident electron from the FM lead with energyEand spins, the wave functions in the two regions of the FM/ISC junction can be written as

withsˉ=-s.The coeffciientsand(orand)are the reflection coefficients(or transmission coefficients)for the electron and the hole, respectively.The functionsfe,s(ˉs)andfh,s(ˉs)(orge,s(ˉs)andgh,s(ˉs)) are the eigenvectors describing electron and hole with spins(ˉs)in the FM region(or ISC region),respectively.[32,34]Based on the boundary conditions

we can obtain two AR probabilities

whereqe,sandqh,s(ˉs)are the longitudinal wavevectors of the electron and hole states in the FM region.When an electron with spinsfrom one valley moves to the FM/ISC interface,as shown in Fig.1(b),RsˉsArepresents the normal AR for the reflected hole with opposite spin ˉs, whileRssArepresents the equal-spin AR with the same spinsdue to the spin-triplet pairing in the ISC.Note that the incident electron and the reflected hole always belong to opposite valleys,because that the Cooper pair in the ISC always forms from two electrons with opposite valleys.Below,we will show that the feature of AR probability strongly depends on the valley degree of freedom due to the irradiation of the circularly polarized light.

3.Results and discussion

In this section, we will discuss the valley-dependent equal-spin AR, normal AR, and spin transport controlled by the light, the chemical potential, and the magnetization direction.The superconducting gap is fixed asΔ=1.0 meV.The exchange energyMand Ising SOC strengthλsare set asM=30.0 meV andλs=10.0 meV for convenience.The symbolRηs?ˉηs(ˉs)in the following represents the AR probability that an incident election with spinsnear valleyηis reflected as a hole with spins(ˉs) near opposite valley ˉη=-η.The units ofλv,E,μFM,andμISCare meV.

First, we discuss the normal AR process when the magnetization vector is in the out-of-plane direction with the polar angleθ= 0.All the AR probabilities are independent of the azimuthal angleφ, so we takeφ= 0 below.Figure 2 shows the AR probabilitiesRK↓?K＇↑andRK↑?K＇↓as functions of the potentialμFMand the lightλvatθ= 0.0,E= 0.0, andμISC= 0.0.It can be found that only the normal AR could occur and equal-spin AR does not exist,where the incident electron and reflected hole belong to opposite spins and opposite valleys, due to the Cooper pairs|KK＇,↓↑〉,|KK＇,↑↓〉 in the ISC being valley singlet with itsz-direction spin componentSz= 0.RK↓?K＇↑andRK↑?K＇↓take place in different areas.HereRK↓?K＇↑andRK＇↑?K↓are equal and occur in the same areaμFM＞|λv-M| [see Fig.2(a)].In fact, considering an incident electron fromK ↓band with the incident energy in the superconducting gap,the

Fig.2.AR probabilities(a)RK↓?K＇↑and(b)RK↑?K＇↓versus potentialμFM and light λv at θ=0.0,E=0.0,andμISC=0.0.The boundaries of AR probability are labelled by the dash curves λv=±μFM±M,which are the critical values of the half-metal phase.

Next,we consider that the magnetization vector is in the in-plane direction withθ=π/2(i.e., in thex-direction).For thex-direction,both the spin-singlet andSx=±1 spin-triplet Cooper pairs can exist in ISC.This is essentially different from the case ofz-direction,where onlySz=0 Cooper pairs exist in ISC.Thus,the AR process would become intriguing.Figure 3 presents the AR probability as a function of the potentialμFMand the lightλvwhen the electron injects from(a)-(d)Kvalley and(e)-(h)K＇valley atθ=π/2,E=0.0,andμISC=0.0.Interestingly, the equal-spin AR appears due to theSx=±1 spin-triplet Cooper pairs|KK＇,?〉,|KK＇,?〉 [see Figs.3(b),3(c),3(f)and 3(g)].In the equal-spin AR process,the incident electron and reflected hole possess the same spins but opposite valleys.The normal AR still survives[see Figs.3(a),3(d),3(e) and 3(h)].The equal-spin AR and normal AR include eight kinds of AR processes, which exhibit some interesting features.

(1) Various AR processes occur in different areas, depending on the spin and valley related band structure controlled by the potentialμFMand the lightλv.Compared to the normal AR, the equal-spin AR probabilityRK(K＇)→?K＇(K)→occurs in a wider area [see Figs.3(b) and 3(f)], whileRK(K＇)←?K＇(K)←occurs in a narrower area[see Figs.3(c)and 3(g)], which can be changed by adjusting the magnetization and the light.

(2) Contrary to the situation atθ=0 in Fig.2, the normal AR probabilitiesRK→?K＇←andRK＇←?K→(RK←?K＇→andRK＇→?K←)are no longer the same atθ=π/2,as shown in Figs.3(a)and 3(h)[Figs.3(d)and 3(e)].The reason is that for an incident electron with its spin in thex-direction, the four reflection processes (the normal reflection, the spin-flip reflection,the normal AR,and the equal-spin AR)occur at the FM/ISC interface,leading to that the scattering matrix is 4×4 and the matrix elements (various reflection probabilities) are in principle mutually unequal.

(3) In the presence of the light, the equal-spin AR and normal AR become sensitive to the valley degree of freedom.Due to the influence of the left and the right circularly polarized light on the character of the two valleys,the Hamiltonians between the two valleys satisfy

in the FM lead.Thus, the AR near the two valleys are symmetric with respect toλv=0,i.e.,

such as the AR probabilitiesRK→?K＇←andRK＇→?K←[see Figs.3(a)and 3(e)].

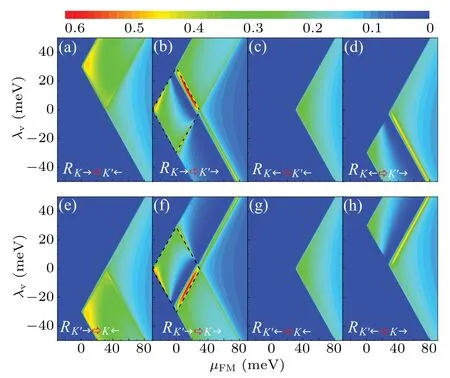
Fig.3.AR probability versus potential μFM and light λv for the incident electron from (a)-(d) K valley and (e)-(h) K＇ valley, at θ =π/2,E=0.0,andμISC=0.0.

(4)Importantly,there exists a special area where only the equal-spin AR probabilitiesRK→?K＇→andRK＇→?K→could take place while other AR processes are completely suppressed [see the rhombic area encircled by the black dashed curvesλv=±μFM±Min Figs.3(b) and 3(f)], which could give rise to a spin supercurrent in ISC, as discussed in Fig.7 in the following.

In order to see clearly the characters of AR, we plot the truncated intersection curves of AR probability as a function of (a) the lightλvand (b) the potentialμFMin Fig.4.Figure 4(a) shows the symmetry between two certain AR processes aroundλv= 0.The AR appears in different regions ofλv.The normal AR probabilitiesRK→?K＇←andRK＇←?K→are finite in the region-μFM+M ＜λv＜μFM+M,whileRK←?K＇→andRK＇→?K←have finite value in the region-μFM-M ＜λv＜μFM-M.The equal-spin AR probabilitiesRK→?K＇→andRK＇→?K→occur in a broad region-μFM-M ＜λv＜μFM+M.As shown in Fig.4(b), the AR probability as a function ofμFMcould be divided into four regions,depending on the spin and valley related energy band in the FM region.There is no AR in the regionμFM＜-M+λv,since the ISC is single-band phase and the FM region has no incident electron mode or/and no reflected hole mode at such a low chemical potentialμFM.Only equal-spin AR probabilitiesRK→?K＇→andRK＇→?K→are nonzero in the region-M+λv＜μFM＜M-λv, because onlySx=1 spin-triplet and valley-singlet Cooper pairs|KK＇,?〉 could be formed in ISC.Two equal-spin AR and two normal AR appear in the regionM-λv＜μFM＜M+λvdue to the existence of Cooper pairs|KK＇,?〉 and|KK＇,?〉.All of the eight AR can take place and all kinds of Cooper pairs can be formed in the regionμFM＞M+λv.

Fig.4.AR probability versus(a)λv atμFM=10.0 meV and(b)μFM at λv=10.0 meV.The values of the other parameters are the same as those in Fig.3.

Figure 5 presents the AR probability as a function of incident energyEatθ=π/2 andμFM=50.0 meV.Whenλv=0 in Fig.5(a), the two valleys in the FM region are degenerate, and so the AR process is independent of valley, that isRηs?ˉηs(ˉs) =Rˉηs?ηs(ˉs).The finiteλvmay break the degeneracy of the valley, leading to the valley-dependent AR [see Fig.5(b)].All the AR probabilities increase slightly with the incident energy in the subgap energyE ＜Δ.WhenμISC=15.0 meV＞λs, the Ising superconducting phase changes to double-band from single-band, and so the normal AR is increased by the spin-singlet Cooper pairs[comparing Figs.5(a)and 5(c)].However,the equal-spin AR is decreased,since the spin-triplet pairing is rather weak for double-band ISC.[26,31]Out of subgap energy regionE ＞Δ,the normal AR probability decreases rapidly from a large value with the increase of the energy, regardless of the values ofλvandμISC.On the other hand,the equal-spin AR probability increases first from zero,then decreases slowly with the increase of the energyEfromΔ.In addition,both normal AR and equal-spin AR present the resonant behavior near the superconducting gap edges,similar to the AR in N/SC junctions.[46]Particularly,the resonant normal AR exhibits a simple peak nearE=Δ,while the resonant equal-spin AR exhibits a peak followed by a dip.

The influence of off-resonant polarized light on the magnetoanisotropy of AR is discussed in Fig.6.The AR probabilities for the incident electron fromKandK＇valleys are defined as

The total AR probability isRK+RK＇.In the presence of magnetization vector, the HamiltonianHηhas the relationσzHη(θ)σ-1z=Hη(-θ), soRη(-θ) =Rη(θ), i.e.,RK(θ)andRK＇(θ)are symmetric aboutθ=0,as shown in Figs.6(a)and 6(b).In the absence of the light withλv=0.0, both AR probabilitiesRKandRK＇are anisotropic with respect to the magnetization directionθ, as shown in Fig.6(a).RKmainly appears in the third and fourth quadrants, whileRK＇mainly occurs in the first and second quadrants.The Hamiltonians between the two valleys can be related by the spin rotation operatorσx,

This indicates that the AR probabilities between the two valleys have the relation

TheRKandRK＇are symmetric aboutθ=π/2.As a consequence, the total AR probabilityRK+RK＇is magnetoanisotropic with periodπ.In the half-metal phase withμFM= 10 meV＜M-λv, only the equal-spin AR can occur (see Fig.3).When the magnetization vectorMis in thezdirection withθ=0, the equal-spin AR is prohibited, then the AR probabilitiesRKandRK＇are zero[see Fig.6(a)].With the increase ofθfrom 0, the equal-spin AR occurs and the AR probabilities appear.When the right circularly polarized light is applied withλv=5.0 meV in Fig.6(b), the symmetric relation equations (13) and (14) between the two valleys are destroyed.RKis decreased butRK＇is increased by the right circularly polarized light,becauseKis the minority valley andK＇is the majority valley in the FM lead.Oppositely,the left circularly polarized light would increaseRKand decreaseRK＇.Thus,the magnetoanisotropy of the total AR probabilityRK+RK＇becomes remarkable and the period becomes 2πinstead ofπin the presence of the light.

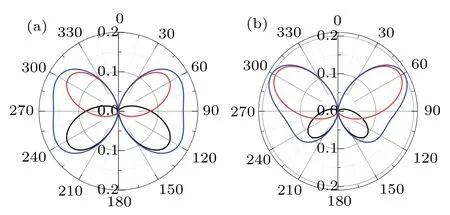
Fig.6.AR probability versus the magnetization direction θ at (a)λv=0.0 and(b)λv=5.0 meV.The black,red,blue curves are for RK,RK＇,and RK+RK＇.Here,μFM=10.0 meV,E=0.0,andμISC=0.0.

Finally,we study the spin transport in this FM/ISC junction.As discussed in Figs.3(b) and 3(f), only the equal-spin ARRK→?K＇→andRK＇→?K→could occur in the rhombic area.In this rhombic area,only theSx=1 spin-triplet Cooper pairs|KK＇,?〉 are generated by the equal-spin AR processes and inject into ISC.There is no injection of the spin-singlet and other kinds of spin-triplet Cooper pairs.As a result, only the Cooper pairs|KK＇,?〉with spinS=1 andSx=1 would flow alongxdirection in the ISC.This implies that a completely spin-polarized supercurrent appears in this rhombic area.If the direction of magnetization is inverted toθ= 3π/2, the spin of the moving Cooper pairs would change toS=1 andSx=-1, and the Cooper pairs|KK＇,?〉 would contribute to the charge current and the spin current.Observably,the direction of the spin-triplet Cooper pairs can be controlled by the magnetization and the light.

Considering thex-direction spin biaseVat the FM/ISC junction, the spin currentIsfrom FM lead flowing into ISC can be written as[35,47]

whereis the equal-spin AR probability,is the spinflip reflection probability,andTsNis the transmission probability.The spin indexs=→,←or+,-in Eq.(15).The Fermi distribution function requiresfL,e→=fL,h←=f(E-eV)andfL,e←=fL,h→=f(E+eV)in the FM lead andfR=f(E)in the ISC.The differential spin conductance can be obtained asGs= dIs/dV.The differential spin conductance for the incident electron fromK(K＇) valley is labeled asGs,K(Gs,K＇),satisfyingGs=Gs,K+Gs,K＇.For the FM/ISC junction, the high spin injection efficiency occurs in the particular halfmetal phase [e.g., in the rhombic area in Figs.3(b) and 3(f)]where there is no spin-flip reflection.

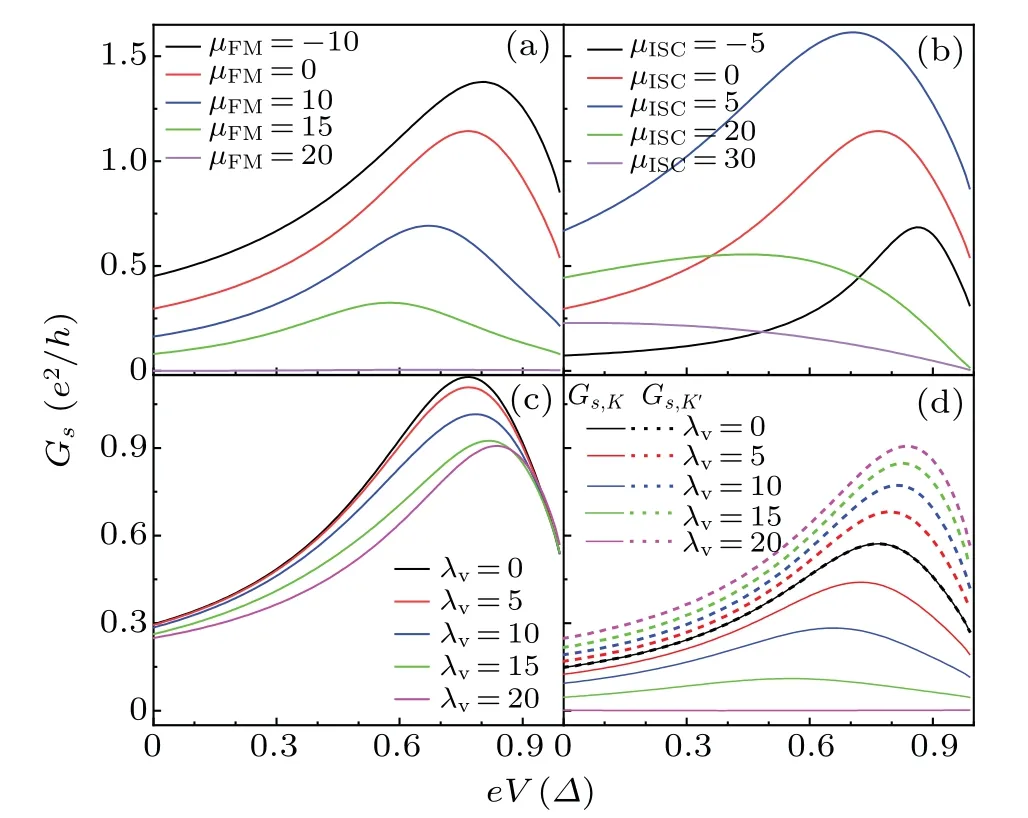
Fig.7.Differential spin conductance Gs versus the finite spin bias eV at zero temperature for different values of(a)μFM,(b)μISC,and(c)λv.(d) Gs,K and Gs,K＇ versus eV for different values of λv.The values of parameters are set as θ =π/2, λv =0.0, μFM =0.0, and μISC =0.0,unless otherwise noted in the figure.

Figure 7 displays the differential spin conductance as a function of finite spin biaseVwith the parametersμFMandλvin the rhombic area.Due to only the occurrence of the equal-spin AR in the rhombic area, the results are the same for thex-direction spin bias and the bias.From Fig.7, one can see that with the continuous increase of spin bias,the differential spin conductance increases slowly at first, and then decreases rapidly after reaching its peak value.In the absence of light withλv=0.0,the differential spin conductanceGs,Kis the same asGs,K＇.The totalGsdecreases with the increase ofμFMand tends to zero atμFM=20.0 meV [see Fig.7(a)].As shown in Fig.7(b),Gsincreases gradually withμISCin the single-band superconducting phase(see the curves withμISC＜λs).On the contrary,Gsdecreases withμISCin the double-band superconducting phase (see the curves withμISC＞λs).The reason is that the differential spin conductance is mainly contributed by the equal-spin AR which mainly occurs in the single-band phase.With the appearance and increase of the light,Gsdecreases relatively[see Fig.7(c)].Remarkably, the differential spin conductanceGs,Kis no longer equal toGs,K＇.It can be seen from Fig.7(d) that asλvincreases,Gs,Kdecreases gradually butGs,K＇increases gradually.Atλv=20 meV, only incident electrons fromK＇valley contribute to differential spin conductance.When the light changes from the right to the left circular polarization,Gs,Kwill increase andGs,K＇will decrease.

4.Conclusion

In summary,we studied the dependence of equal-spin AR on the valley degree of freedom in the light-irradiated FM/ISC junction based on Bogoliubov-de Gennes Hamiltonians.Due to the application of circularly polarized light,the properties of equal-spin AR and normal AR strongly depend on the valley degree of freedom.The resonant behavior of equal-spin AR near the superconducting gap edges is different from that of normal AR.The valley-dependent AR presents certain symmetry about light strength and magnetization angle, which can be understood by the symmetry of the system.The existence ofSx=±1 spin-triplet Cooper pairs leads to a valleydependent spin supercurrent in ISC which can be modulated by the light.Our results should be useful to the potential applications of ISC in spintronics and valleytronics.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant Nos.11974153, 12374034 and 11921005),the Innovation Program for Quantum Science and Technology (Grant No.2021ZD0302403), and the Strategic Priority Research Program of Chinese Academy of Sciences(Grant No.XDB28000000).