Scale adaptive fitness evaluation‐based particle swarm optimisation for hyperparameter and architecture optimisation in neural networks and deep learning
Ye‐Qun Wang | Jian‐Yu Li | Chun‐Hua Chen | Jun Zhang | Zhi‐Hui Zhan
1School of Computer Science and Engineering,South China University of Technology,Guangzhou,China
2School of Software Engineering, South China University of Technology,Guangzhou,China 3Hanyang University,Ansan,South Korea
Abstract Research into automatically searching for an optimal neural network (NN) by optimisation algorithms is a significant research topic in deep learning and artificial intelligence.However, this is still challenging due to two issues: Both the hyperparameter and architecture should be optimised and the optimisation process is computationally expensive.To tackle these two issues, this paper focusses on solving the hyperparameter and architecture optimization problem for the NN and proposes a novel light-weight scaleadaptive fitness evaluation-based particle swarm optimisation (SAFE-PSO) approach.Firstly, the SAFE-PSO algorithm considers the hyperparameters and architectures together in the optimisation problem and therefore can find their optimal combination for the globally best NN.Secondly,the computational cost can be reduced by using multiscale accuracy evaluation methods to evaluate candidates.Thirdly, a stagnation-based switch strategy is proposed to adaptively switch different evaluation methods to better balance the search performance and computational cost.The SAFE-PSO algorithm is tested on two widely used datasets: The 10-category (i.e., CIFAR10) and the 100-category (i.e., CIFAR100).The experimental results show that SAFE-PSO is very effective and efficient,which can not only find a promising NN automatically but also find a better NN than compared algorithms at the same computational cost.
K E Y W O R D S deep learning, evolutionary computation, hyperparameter and architecture optimisation, neural networks,particle swarm optimisation, scale-adaptive fitness evaluation
1 | INTRODUCTION
With the rapid development of deep learning, many neural networks (NNs) have been proposed and have achieved excellent performance in various fields [1–3].However, a new NN is usually designed by human experts with a great number of trials, which is tedious and time-consuming.Moreover,designing novel NNs manually is becoming more and more difficult due to the limitation of existing knowledge.Therefore,in recent years,searching for a new great NN automatically has become a new popular research topic in the community of deep learning and artificial intelligence and obtained successful results in many fields,such as image classification[4],semantic segmentation [5], object detection [6], and natural language processing [7].
Although many methods have been proposed for finding an optimal NN automatically,for example,the neural architecture search (NAS) and the evolutionary deep learning (EDL) algorithms[8],we notice that many of these methods may only find a local optimal NN under a series of predefined fixed hyperparameters.This may be due to these NAS algorithms fixing the NN hyperparameters and only considering searching for the NN architectures.However, both hyperparameters and architectures have significant influences on the NN performance and they interact with each other when designing the NN.Moreover,some studies have shown that hyperparameters and architectures should be considered at the same time in obtaining a great NN.For example, Lewkowyczet al.[9] studied the impact of different learning rates on training architectures, which shed light on the characteristics of architectures trained at different learning rates(i.e.,different hyperparameters).Therefore,rather than only optimising NN architectures, jointly optimising NN hyperparameters and NN architectures is a more effective way of finding the globally optimal NN.
However,the hyperparameter and architecture optimisation(HAO)problem for the NN is very difficult and complex,which poses great challenges to the optimisation ability of the optimisation algorithm.Moreover, when searching for an optimal NN,as training and validating a candidate NN require expensive computational costs (i.e., expensive computational time and computational resources) with adequate epochs and data,evaluating the performance of different candidate NNs would be very computationally expensive.For example,NASV3 costs 800 GPUs to run 28 days[10],and MetaQNN uses 10 GPUs to run 8–10 days[11].Hence,the expensive computational cost is a great challenge for HAO.Therefore,more efficient methods for reducing computational cost are in great need.
Hence, this paper focusses on how to solve the HAO problem effectively and efficiently.Owing to the advantages of excellent optimisation ability and easy implementation for solving complex optimisation problems [12–14], evolutionary computation (EC) algorithms have attracted much attention[15–17] and obtained some promising results in the field of HAO recently[18–20].Therefore,this paper also considers the particle swarm optimisation(PSO)algorithm[21,22],a representative kind of EC algorithm with great optimisation ability,for solving the difficult and complex HAO problems effectively.
In general, the PSO algorithm involves a swarm of particles to solve an optimisation problem, where each particle represents a candidate solution to the optimisation problem.In every generation,the fitness evaluation method(EM)is used to evaluate the fitness values of the particles,that is,the quality of the corresponding solutions represented by particles, so as to help select better particles to approach the global optimum.When solving the HAO problem via PSO, each particle represents a candidate NN,and the EM needs to train and validate the candidate NN to get the corresponding fitness value.As mentioned before, training and validating NNs require expensive computational costs, the EM for calculating the fitness values of the NNs in PSO is thus very computationally expensive to perform.This leads to a huge challenge to the efficiency of the PSO algorithm for solving the HAO problem.Recently,the idea of scale-adaptive fitness evaluation(SAFE)is put forward by Wuet al.[23]that multiple EMs with different scales can work cooperatively for solving expensive optimisation problems (EOP), where EOP refers to the optimisation problem with the computationally expensive EM[24].Inspired by this, we design multiple EMs with different scales for the HAO problem and then propose a novel SAFE strategy together with a stagnation-based switch strategy to adaptively utilise the designed EMs for solving the HAO problem.
Based on the above, we develop a light-weight SAFEbased PSO (denoted as SAFE-PSO) algorithm by integrating the PSO with the SAFE strategy and the stagnation-based switch strategy, so as to solve the HAO problem effectively and efficiently.The main advantages and contributions of our work are summarised as follows.
(1) We consider that different NN architectures can obtain better performance with different specific NN hyperparameters, and based on this, we study how to optimise both the hyperparameters and architectures at the same time.Therefore, our algorithm can find the optimal combination of NN hyperparameters and NN architectures, avoiding finding the locally optimal NN architectures without considering various NN hyperparameters.
(2) The novel SAFE strategy for the HAO problem is proposed.This strategy uses a series of EMs with different accuracy scales to collaboratively accomplish the entire evolutionary process for HAO.Specifically, the lowaccurate EM requiring less computational cost can play a role in filtering poor solutions in the early stage of evolution, and the high-accurate EM requiring more computational cost is beneficial to finding more fine solutions in the later stage of evolution.Hence,our new SAFE strategy can enhance the search ability and reduce the computational cost in HAO by making full use of the characteristics of different EMs.
(3) The stagnation-based switch strategy is further proposed to assist the SAFE strategy.The stagnation-based switch strategy adaptively switches different scale EMs by judging the stagnation state of the SAFE-PSO algorithm so that appropriate EMs can be adaptively used in different evolutionary stages.
The rest of this paper is organised as follows.In Section 2,we briefly introduce the basic framework of PSO and related work.In Section 3, the SAFE-PSO algorithm is described in detail.In Section 4,we present the experiments and discuss the results.Finally, conclusions are given in Section 5.
2 | BACKGROUND
2.1 | Particle swarm optimisation

2.2 | Related work
This paper proposes the SAFE strategy and the stagnationbased switch strategy to reduce the required computational cost in searching for an optimal NN.Therefore,in this part,we briefly introduce some representative work on how to reduce the computational cost of evaluating candidate NNs during searching for an optimal NN.
Firstly,computational cost can be reduced by reducing the search space to reduce the number of NN candidates.Considering that manually designed NNs tend to be constructed by some similar modules(e.g.,blocks or cells),the search space can be reduced via simpler encoding of NNs based on modules.For example,Zophet al.[30]proposed a new NASNet search space that reduced the search space from the whole network to an architecture building block.The searched block would be stacked to form a complete NN in a predefined way.In this way,the search space is greatly reduced and the searched block can be transferred to a larger dataset.Moreover,Chenet al.[31]only considered the key rather than all hyperparameters and architectures during the optimisation to narrow the search space and reduce the required computational cost.
Secondly,some effective EMs were proposed to accelerate the evaluation process of the candidate NNs,such as parameters sharing [32, 33], surrogate model [34–38], low-fidelity strategy[39, 40], and distributed technology [41–44].Phamet al.[32]proposed parameters sharing to reduce the computational cost.That is,the search space is treated as a large convolutional graph and a new candidate NN can be viewed as a subgraph,so that parameters can be shared among candidate NNs.Although parameters sharing is 1000 times faster than normal EMs[33],it is hard to explain why the parameters sharing is feasible.Moreover, as training and validating each candidate NN to obtain the performance is the main reason for the computationally expensive cost, the surrogate model is proposed to replace expensive EMs.The surrogate model can predict the performance of candidate individuals, which is widely used in solving the EOP [37, 38].Therefore, utilising the surrogate model can avoid training and validating all candidate NNs,so as to reduce the computational cost of finding good NNs.For example, Liet al.[19] proposed a novel surrogate-assisted approach to solve the HAO problem, which has obtained promising results on not only both 10- and 100-category image classification problems,but also a healthcare application in real world.Different from the surrogate model that predicts the NN performance,the low-fidelity strategy[39,40]is to train candidate NNs for only a few epochs and then validate candidate NNs on a small dataset.Comparing the strategy that training candidate NNs to convergence on a large dataset, the low-fidelity strategy can greatly reduce the total epochs of training and therefore reduce the total computational cost.Finally,distributed technology is also effective to speed up the evaluation process [41, 42].Guoet al.[43] utilised distributed PSO and Liuet al.[44]utilised distributed differential evolution to evaluate multiple candidate NNs at the same time, which indeed can improve the evaluation speed.
In summary, the automatically searching for an optimal NN has become a popular research topic that has attracted increasing attention in the community of deep learning and artificial intelligence.Hence,how to design a new and efficient method to reduce computational time and computational resources is of great research significance for solving more complex HAO problems, which is conducive to further promoting the research of HAO.
3 | THE SAFE‐PSO ALGORITHM
The idea of the SAFE is to solve the EOP by adopting the low-accuracy scale EMs to quickly locate promising regions and utilising the high-accuracy scale EMs to refine the solution accuracy[23].As the HAO problem can also be regarded as an EOP with expensive EMs for evaluating the true performance of candidate NNs, this paper proposes the SAFE-PSO algorithm for solving the HAO problem.In the SAFE-PSO algorithm, we design a series of EMs with different accuracy scales and computational costs, so as to cooperatively accomplish the entire evolutionary process.In the following contents, we will introduce the solution encoding, the fitness evaluation,the SAFE strategy,and the stagnation-based switch strategy one by one in detail.Then, the complete SAFE-PSO algorithm framework is given at last.
3.1 | Solution encoding
HAO refers to finding the combination of NN hyperparameters and NN architectures with the best performance in a specific search space.Therefore, in HAO, each hyperparameter or architecture of the NN would be regarded as a variable to be optimised,and all these variables form the whole search space.Then,in PSO,the encoding space of particles is determined by the search space of HAO.That is,each dimension of a particle represents a variable of the HAO problem and each particle represents a combination of hyperparameters and architectures for a candidate NN.Moreover, as some hyperparameters are discretevariablesandPSOisforsolvingcontinuousoptimisation problems,the search space of the discrete variables is mapped to the continuous encoding space during the optimisation.That is,the PSO encodes the discrete variables in a continuous search space and updates these variables in the continuous search space.When the encoding of the particle is constructed as a new NN,thevalueofthediscretevariableswillbedecodedbyroundingthe continuous value to the nearest discrete value.
For example, suppose that we will optimise the initial learning rate (i.e., hyperparameters) and type of each hidden layer (i.e., architectures) for a NN.Then, the SAFE-PSO is encoded with 2 dimensions(i.e.,the first dimension represents the initial learning rate and the second dimension represents the type of each hidden layer).Since the value of the initial learning rate is continuous, the encoded range of first dimension is the same as the value range of the initial learning rate.Since the type of each hidden layer can be average pooling or max pooling, the variable of the second dimension is discrete and the corresponding search space is {average pooling, max pooling}.So, the encoded range of the second dimension would be [0,1].During decoding, the range [0, 0.5) is for‘a(chǎn)verage pooling’ and the range [0.5, 1] is for ‘max pooling’.
3.2 | Fitness evaluation
In this part, we describe how to evaluate the fitness values of particles.For particlei, since the positionXirepresents a combination of hyperparameters and architectures,we need to construct the corresponding candidate NN (i.e., a potential solution) based onXi.Then, we use the EM to train this constructed NN on
the training data, and the corresponding performance(e.g.,classification accuracy)is calculated on the validation data.Finally, the performance of the
constructed NN is adopted as the fitness value of particlei.The fitness evaluation process for a single candidate NN(i.e.,a potential solution)is shown in Algorithm 1,and a more detailed introduction to the EM will be given in the next part.

Algorithm 1 The fitness evaluation process Inpu t: Xi —the position of the particle i.Output: Fiti—the fitness value of the particle i.1: Begin 2: Use Xi to construct a corresponding new NN;3: Use the EM to train the constructed NN on the training data;4: Calculate the performance of the constructed NN on the validation data as the fitness value Fiti;5: Return Fiti.6: End
3.3 | The SAFE strategy with multi‐scale EMs
The SAFE strategy is the key to the SAFE-PSO algorithm.The core of the SAFE strategy is to use a series of multi-scale EMs to collaboratively accomplish the entire evolutionary process.Hence, we would design a series of EMs.Moreover,the low-fidelity strategy is widely used and its characteristic fits the SAFE strategy.That is, within a certain range, with the increase of training epochs, the accuracy and computational cost are both getting higher and higher.Therefore, we can design different EMs based on the low-fidelity strategy by adjusting the number of the training epochs to obtain various EMs with different accuracy scales and computational costs.Note that too few EMs are insufficient for adequate evaluation scales while too many EMs would be redundant.Therefore,in this paper, we design three EMs with different levels of accuracy scales and computational costs, where the EM with higher accuracy will need more computational cost.Herein,the differences in accuracy and computational cost are determined by the number of training epochs.Based on this consideration,in the early stage of evolution, we utilise the rough EM with few training epochs, which is with the lightest computational cost, to filter poor candidates and quickly locate promising regions.In the midterm, we use a more accurate but more expensive EM with a medium number of training epochs to explore the promising regions.Finally, we use the most accurate EM with more training epochs,which is with the heaviest computational cost,to refine the promising regions in the late stage.
Our SAFE strategy has two advantages when compared with the conventional strategy that only uses one EM with a fixed number of training epochs throughout the whole evolutionary process.Firstly,in the early evolutionary stage,the performance of early termination of training(e.g.,only training candidate NNs with few epochs) can guide the search and locate the promising regions fast,which helps to accelerate the search process.Secondly, the EM with more training epochs can get more refined accuracy, and hence can help to find a better solution in the later evolutionary stage.Therefore, our SAFE strategy can balance the solution accuracy and the computational cost.
3.4 | The stagnation‐based switch strategy
After designing a series of EMs, we further consider how to adaptively use the appropriate EM at different evolutionary stages.Hence,we further propose the stagnation-based switch strategy, which adaptively switches EMs based on the stagnation state information of the algorithm.Specifically, when the global optimal value of the algorithm (i.e., theGbest) is not updated for consecutive generations, the algorithm may fall into a local optimum,and it is difficult for the algorithm to find a better solution.Therefore, we record the consecutive stagnation generations as the stagnation state information of the algorithm and utilise the stagnation state information as the switching condition for EMs.That is, we take the consecutive stagnation generations as the switch condition, and once the consecutive stagnation generations reach a predefined maximal consecutive stagnation generation, the algorithm will automatically use the next EM to evaluate candidates.Therefore,the algorithm can achieve self-adaptation to the EMs with different scales.
The detailed switch process is shown in Figure 1 and described as follows,where the right arrows indicate the switch direction of EMs,and the loop arrows indicate that the switch condition is not reached and therefore retain the current EM unchanged.In the SAFE-PSO algorithm,all available EMs are EM1, EM2, and EM3with increasing accuracy and computational cost, and the initial EM is EM1.That is, EM1has the lowest accuracy and computational cost, while EM3has the highest accuracy and computational cost.Specifically, we set the maximal consecutive stagnation generations asSand the current consecutive stagnation generations in thegthgenerationsg,withs1=0 in the first generation.Then,updatesgand switch the EM according to the following two steps in thegthgeneration.
Step 1: Updatesg.Thesgis calculated as
whereGbestgandGbestg-1represent the global bestGbestin thegthgeneration and(g–1)thgeneration,respectively.sg-1represents the current consecutive stagnation generations in the (g– 1)thgeneration.
Step 2: Switch the EM.IfsgequalsS, the EM will be switched from the current EM to the next EM(e.g.,switch EM from EMkto EMk+1,k=1 or 2.),and thesgwould be reset to zero.When the current EM is EM3and the switch condition is met again, the SAFE-PSO algorithm ends.
A complete description of the stagnation-based switch strategy for assisting the SAFE strategy is shown in Algorithm 2.In every generation,we judge whether the global bestGbestis updated.If theGbestis updated, the number of current
consecutive stagnation generations will be set to 0.Otherwise, the value of the number of current consecutive stagnation generations will be added by 1.Then, we further judge whether the number of current consecutive stagnation generations has reached the maximal consecutive stagnation generations.If reached,the current EM will be switched to the next EM.

images/BZ_310_1357_2535_1451_2613.pngAlgorithm 3 The framework of the SAFE-PSO algorithm Input:A swarm with N particles,S.//S means the maximal consecutive stagnation generations.Output: The global best Gbest in the last generation.1.Begin 2.Randomly initialise velocity V and position X of N particles;3.EM = EM1;4.Evaluate the fitness value of each particle by Algorithm 1;5.While the end condition is not met 6.Randomly generate the inertia weight ω between 0.4 and 0.6;

F I G U R E 1 The switch process of EMs, where right arrows indicate the switch direction of EMs, and the loop arrows indicate retaining thecurrent EM unchanged if the switch condition is not reached

Algorithm 2 The SAFE strategy with the stagnationbased switch strategy Input:Gbestg-1—the global best Gbest in the(g - 1)th generation;Gbestg—the global best Gbest in the gth generation;EMcur—the current EM;EMnext—the next EM;S - the maximal consecutive stagnation generations;sg-1—the number of current consecutive stagnation generations in the (g - 1)th generation.Output: EM—the EM adopted to evaluate particles;sg—the number of consecutive stagnation generations in the gth generation.1.Begin 2.If Gbestg = = Gbestg-1 3.sg = sg-1 + 1;4.If sg ≥S 5.Switch EM from EMcur to EMnext, and reset sg = 0;6.End If 7.Else 8.sg = 0;9.End If 10.Return EM and sg.11.End
3.5 | The complete SAFE‐PSO algorithm
Three main parts of the SAFE-PSO algorithm to solve the HAO problem are shown in Figure 2, and the complete framework of the SAFE-PSO algorithm is shown in Algorithm 3.The SAFE-PSO has the following five steps.
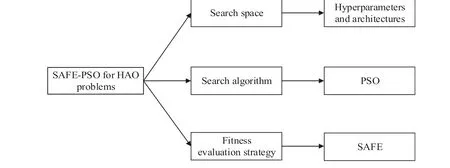
F I G U R E 2 The three main parts of scale-adaptive fitness evaluation-based particle swarm optimisation (SAFE-PSO) for the hyperparameter and architecture optimisation (HAO) problem, include the search space composed of hyperparameters and architectures, the search algorithm using PSO, and the fitness evaluation using the SAFE strategy

7.For particle i in the gth generation 8.Update Vi and Xi of particle i;9.Evaluate the fitness value of particle i via Algorithm 1;10.Update the personal best Pbesti of particle i and the global best Gbestg;11.End For 12.Update EM and sg by Algorithm 2;13.End While 14.Return Gbest.15.End?
Step1 The SAFE-PSO algorithm randomly initialises the velocity and position of each particle, sets the current EM as EM1, and sets the number of the maximal consecutive stagnation generationsS.
Step2 Evaluate each particle by the current EM (as shown in Algorithm 1),andGbestis obtained by comparing the fitness values of all particles.
Step3 Update the velocity and position of each particle with Equation (1) and (2), and evaluate the fitness value of each particle via Algorithm 1.
Step4 Update the value of current stagnation generations and EM by the stagnation-based switch strategy (as shown in Algorithm 2).
Step5 If the end condition is not met,the algorithm goes back to Step 2 and repeats Step 2 to Step 4.Otherwise,theGbestis output, and the algorithm finishes.
4 | EXPERIMENTAL STUDIES
4.1 | Test benchmarks and evaluation metrics
Image classification is one of the significant and popular tasks in deep learning,which refers to the use of the NN to determine which category a picture belongs to.In this paper, we use the SAFE-PSO algorithm to optimise hyperparameters and architectures of the NN and apply the optimised NN to the image classification task.The CIFAR10[45]and CIFAR100[45]are two image classification tasks that have been widely studied and used as experimental test benchmarks in literature.Therefore, it is appropriate to choose them as experimental test benchmarks in this paper.These two tasks are described as follows.
CIFAR10:The CIFAR10 consists of 60,000 32×32 images in 10 categories and is divided into two parts:a training set and a test set.The training set contains 50,000 images with 5000 images per category, and the test set contains 10,000 images with 1000 images per category.
CIFAR100:The CIFAR100 is like CIFAR10;it also consists of 60,000 32×32 images and is divided into a training set with 50,000 images and a test set with 10,000 images.However,CIFAR100 and CIFAR10 differ in the number of categories included.CIFAR100 has 100 categories, and each category includes 600 images.So, in the training set and test set, each category has 500 images and 100 images, respectively.Since CIFAR100 has more refined categories and contains fewer images per category,CIFAR100 is more difficult than CIFAR10.
Some samples of CIFAR10 and CIFAR100 are shown in Figure 3.Furthermore, according to the data preprocessing suggested in some literature [3], for both CIFAR10 and CIFAR100,we use the random horizontal flip with a probability of 0.5,the random crop 32×32 patches with 4 pixels padding on each border,and the normalisation over RGB channels.
In the experiments, the effectiveness and efficiency of the algorithm are both considered.For the effectiveness, classification accuracy in percentages and the number of parameters in millions of the optimal NN obtained by the algorithm are compared.As for the efficiency,the total number of days on a single GPU required by the algorithm in a single run(denoted as GPU days) and the specific GPU cards used by the algorithm(denoted as GPU type)are compared.Therefore,classification accuracy,the number of parameters,GPU days,and GPU type are used as evaluation metrics,and the experimental results are described from these four popular evaluation metrics.
4.2 | Search space

F I G U R E 3 Some samples from (a) CIFAR10; (b) CIFAR100.The left column represents the label of samples in each corresponding row
To solve the HAO problem for the image classification task,we need to design the search space with hyperparameters and architectures to be optimised.Considering that the image classification task generally uses convolutional neural networks(CNNs) and ResNeXt [46] is a representative CNN, we use ResNeXt as the basic CNN model to be optimised in this paper.
We choose ResNeXt with 28 convolutional layers as our basic model in the experiments and hope to find a promising result.We denote ResNeXt with 28 convolutional layers as ResNeXt-28, and the complete ResNeXt-28 is illustrated in Figure 4a, where the curve represents the residual connection.We can see that ResNeXt-28 is mainly constructed with residual connection and multibranch architecture, with the first convolutional layer, an activation function after the first convolutional layer, nine basic blocks, a pooling layer, and a fully connected layer in the last.Moreover,a block consists of three convolutional layers and two activation functions(as shown in Figure 4b and c).Herein, to maintain the modularity and simplicity of ResNeXt-28, we guarantee that all activation functions contained in an optimised block are of the same type and all branches in a block are the same.Hence, 23 variables need to be optimised, including the kernel size of 10 convolutional layers (the first convolutional layer and every convolutional layer between 1 × 1 convolutional layer in every block.Note that the 1 × 1 convolutional layer is used for increasing and decreasing dimensionality and therefore it does not have to be optimised), the type of 10 activation functions(the first activation function after the first convolutional layer and nine activation functions in nine blocks), the type of the pooling layer in the last,the based width of a branch in the first block,and the initial learning rate.The detailed searching range and encoding range of all variables to be optimised for SAFEPSO are shown in Table 1,where thex1tox21are architecture variables, whilex22andx23are hyperparameter variables.
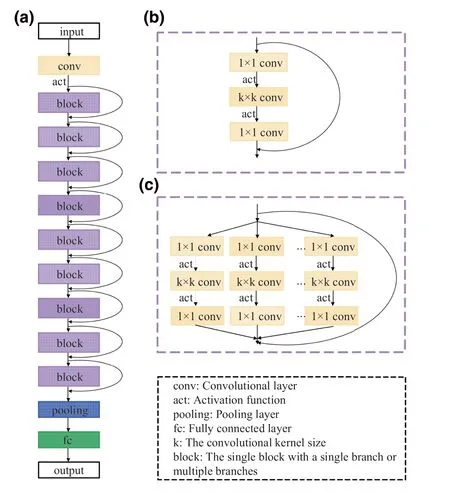
F I G U R E 4 The illustration of the neural network (NN) to be optimised.(a) The complete ResNeXt-28, (b) a single block with a single branch, and (c) a single block with multiple branches, where the curve represents the residual connection
4.3 | Experimental setting
The detailed settings of the SAFE-PSO algorithm and the CNN are as follows.
For the SAFE-PSO, we design EM1, EM2, and EM3with training 5, 15, and 25 epochs, respectively, to collaborate to accomplish the entire evolutionary process.We setS= 5 as switch conditions (i.e., maximal consecutive stagnation generations) between EMs.The population size is set to 15, acceleration factorsc1andc2are both set to 2.0,and inertia weightωis randomly generated within [0.4, 0.6] in every generation.We run the SAFE-PSO three times and the best result among the three runs is reported.
For the CNN, one of the characteristics of ResNeXt-28 is that each branch of the ResNeXt-28 is the same.Hence,during the search process of the SAFE-PSO algorithm, we set the number of the branch to 1 for ResNeXt-28.In addition, afterthe SAFE-PSO has found the best hyperparameters and architectures of the ResNeXt-28, we can use the training set to train its parameters and use the test set to obtain its true performance(e.g.,the classification accuracy).However,during the search process of SAFE-PSO,we cannot use the test set,so we need to conduct the training data and validation data to evaluate the performance of the candidate CNNs (i.e., the fitness value).Hence, we randomly select 2500 samples per category from the training set of CIFAR10 to conduct the dataset for evaluating the fitness values of SAFE-PSO.Specifically, 90% of samples in the dataset (i.e., 2250 samples per category) are used as training data and 10% of samples in the dataset (i.e., 250 samples per category) are used as the validation data.Moreover,the images of each category in the training data and validation data do not overlap.That is, every candidate CNN would be trained on the training data and validated on the validation data to obtain the corresponding performance (we use the classification accuracy as the performance of the candidate CNN, which is also the fitness value of the candidate CNN) during the search process.

T A B L E 1 The search space based on ResNeXt-28
As for the final new optimal CNN, we would add the number of the branches to 8 and the new optimal CNN with 8 branches is named SAFE-PSO-obtained CNN (SAFEPSOCNN).Note that the SAFEPSO-CNN is obtained on the subset(i.e., the training data and validation data) of CIFAR10,and we also test it on CIFAR100.That is,the SAFEPSO-CNN will be trained on the training sets of CIFAR10 and CIFAR100 with 300 epochs,and tested on their test sets to obtain the true performance for experimental comparisons,respectively.Since CIFAR10 and CIFAR100 have similar domains,it is reasonable to directly apply SAFEPSO-CNN to CIFAR100, and this can also show the transferability of our SAFEPSO-CNN.The transferability of our SAFEPSO-CNN is also an advantage and contribution of our work.
4.4 | Comparisons with state‐of‐the‐art networks
In this part,we compare our SAFEPSO-CNN with some stateof-the-art (SOTA)NNs proposed in recent years,to show the effectiveness and efficiency of our SAFE-PSO algorithm.The comparison results are shown in Table 2, where ResNet-110 means ResNet with 110 layers, ResNeXt-28 means ResNeXt with 28 layers and 8 branches,and‘-‘indicates that the network does not report its corresponding results.Furthermore,we use boldface and underline to indicate the best result and the second-best result in the comparisons, respectively.Due to resource constraints,the results of the compared networks are obtained according to the reported results in the literature.Moreover,as the ResNeXt-28 with 8 branches[46]is the basic model of our SAFEPSO-CNN and Ref.[46]did not report the detailed classification accuracy of ResNeXt-28 with 8 branches on the CIFAR10 and CIFAR100,we implement the ResNeXt-28 with 8 branches, where the hyperparameters and architectures of the implemented ResNeXt-28 are the same as those in Ref.[46].Except for the hyperparameters and architectures(i.e.,23 optimised hyperparameters and architectures shown in Table 1), other configurations of SAFEPSO-CNN and the implemented ResNeXt-28 are the same.Note that some CNNs with the same parameter scale and computational cost(i.e.,the GPU days and type)on CIFAR10 and CIFAR100 are presented in the same line.
As is shown in Table 2, we can see that our SAFE-PSO algorithm costs 1 Nvidia 3090 GPU card with 2.5 days to find the SAFEPSO-CNN.The SAFEPSO-CNN with 29 million parameters obtains 95.98% accuracy on CIFAR10 and 81.33%accuracy on CIFAR100.The effect of our SAFEPSOCNN is better than most of the compared NNs.Moreover,the computational cost required by the SAFE-PSO algorithm is much lower than most SOTA algorithms.Hence, our SAFEPSO is effective and can find a promising result in a relatively short time.
Firstly,our SAFEPSO-CNN obtains a higher classification accuracy than seven recent years' manually designed networks on CIFAR10 and CIFAR100.Specifically, when comparing with the basic model ResNeXt-28, our SAFEPSO-CNN is smaller than the ResNeXt-28 (i.e., 29 million VS 34 million)and higher than ResNeXt-28 with 0.62% on CIFAR100.Besides the ResNeXt-28, DenseNet-BC performs best among other six manually designed networks on both CIFAR10 and CIFAR100, but our SAFEPSO-CNN is also better than DenseNet-BC.To be specific,SAFEPSO-CNN is even higher than DenseNet-BC with 0.49% and 3.61% on CIFAR10 and CIFAR100, respectively.
Secondly, our SAFEPSO-CNN also obtains a promising result when compared with twelve automated designed NNs.Compared with nine automated designed networks obtained by non-PSO-based algorithms,our SAFEPSO-CNN shows pretty good performance on both two datasets.On CIFAR10,SHEDA-CNN performs best,and the accuracy of SAFEPSOCNN has only 0.38% lower than that of SHEDA-CNN.However, on CIFAR100, our SAFEPSO-CNN outperforms SHEDA-CNN, with the accuracy of SAFEPSO-CNN being higher at 2.49%than that of SHEDA-CNN,which suggests that SAFE-PSO can find a better NN for more complex classification tasks.Although SMASHv2, AE-CNN, and SAFEPSOCNN obtain similar performance on CIFAR10, the performance of SAFEPSO-CNN is much better than SMASHv2 and AE-CNN on CIFAR100.Furthermore,the computational time required for searching AE-CNN is much more expensive than that of SAFEPSO-CNN(i.e.,27 GPU days vs.2.5 GPU days).While compared with three automated designed NNs obtained by PSO-based algorithms,our SAFEPSO-CNN also performs better than those NNs obtained by other PSOs on both CIFAR10 and CIFAR100.Based on the above,the superiority of the SAFE-PSO has been validated.

T A B L E 2 Comparison with some state-of-the-art NNs on CIFAR10 and CIFAR100
4.5 | Effects of the SAFE strategy
In this part, we study the effectiveness of the SAFE strategy.We compare the effect of the SAFE-PSO algorithm with and without the SAFE strategy for solving the HAO problem.In detail, the SAFE strategy is compared with the other three EMs that only use EM1, EM2, or EM3separately during the entire evolutionary process.For a fair comparison, the algorithms with different EMs use the same computational time and computational resources (i.e., using the same computational time on the same GPU cards), which are the same as SAFE-PSO used.This way, the algorithms with different EMs run different numbers of generations.The settings of SAFE-PSO and CNN remain the same as described above.
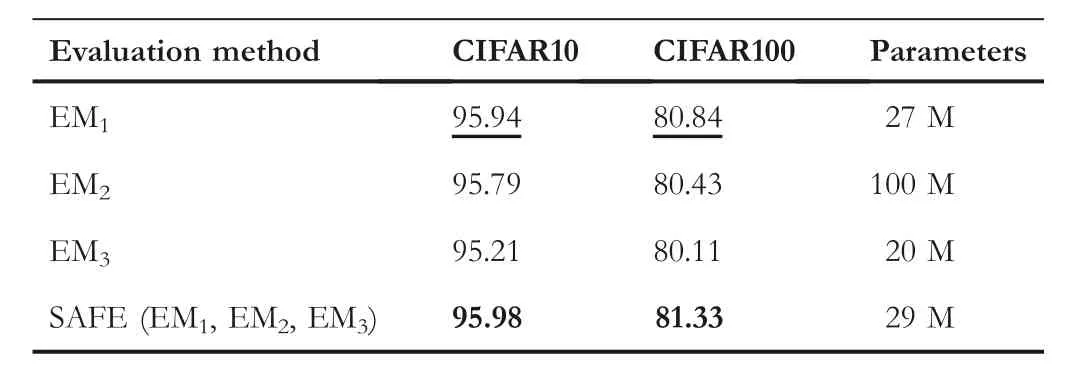
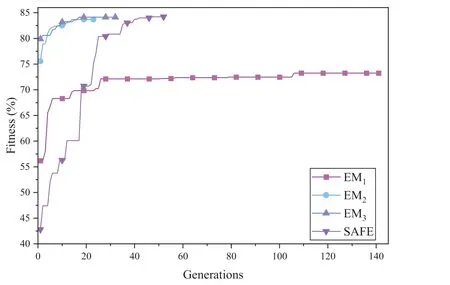
The experimental results are given in Table 3 and described as follows.The SAFE-PSO algorithm with the SAFE strategy performs better than the other three variants without the SAFE strategy on both two datasets.That is,SAFE-PSO with SAFE strategy can improve the accuracy of the algorithm's solution than that of SAFE-PSO without the SAFE strategy with the same computational cost.
We further draw the evolutionary curve of the SAFE-PSO algorithm with these four EMs, as is shown in Figure 5,where they-axis represents the fitness value of theGbestin every generation obtained via Algorithm 1.For EM1, it requires the least computational time to evaluate every candidate NN.Therefore, more candidate NNs can be searched within the same computational time (i.e., the algorithm can iterate more generations).However, the algorithm with EM1can only find a rough solution, and is easy to fall into a local optimal solution, hence the result of using EM1is not as good as that of using the SAFE strategy.Moreover, Table 3 shows that EM2and EM3perform worse on both CIFAR10 and CIFAR100 than EM1.This may be due to the that EM2and EM3need more computational time to evaluate every candidate NN, which means that fewer candidates can be found by EM2and EM3(i.e.,the algorithm with EM2or EM3will iterate fewer generations than the algorithm with EM1in one run with the same total computational time).Hence, the search ability of the algorithm using EM2or EM3is limited at the same computational time.As for the SAFE strategy,different EMs are reasonably used at different stages of the evolution.Therefore,the SAFE strategy can not only help the SAFE-PSO algorithm to find more candidates with the same computational cost but also help to improve the search ability of the SAFE-PSO algorithm, which shows that the SAFE strategy indeed can balance the computational cost and optimisation accuracy.
T A B L E 3 Performance Comparison of NNs found by the scaleadaptive fitness evaluation-based particle swarm optimisation(SAFE-PSO)algorithm with and without the SAFE strategy on CIFAR10 and CIFAR100
4.6 | Investigations of the EMs in the SAFE strategy
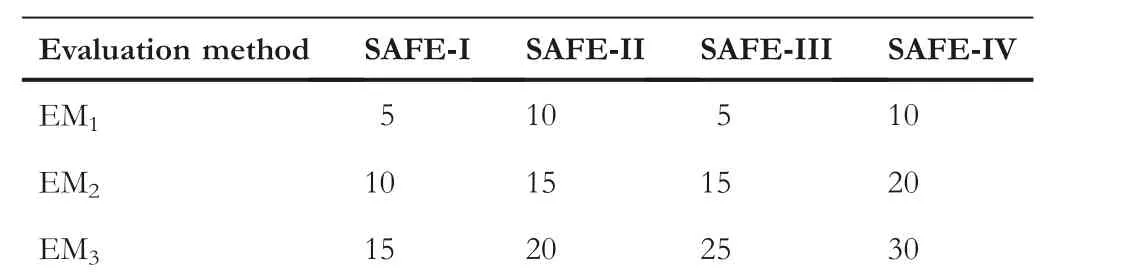
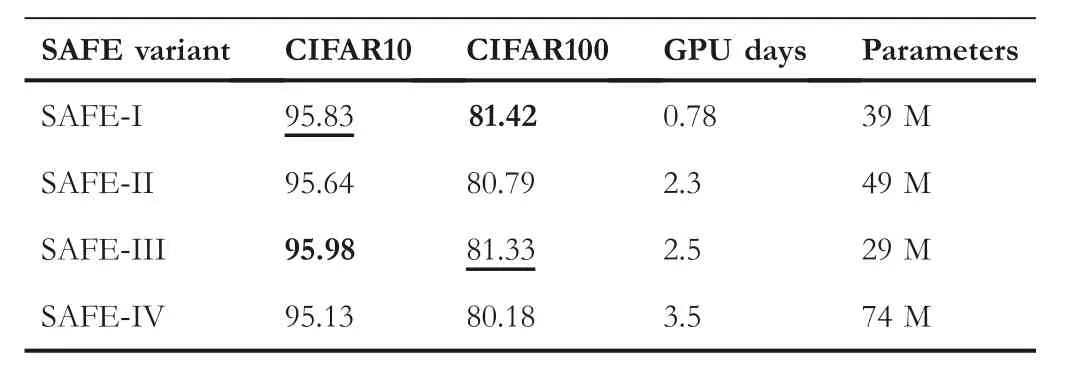
To reduce the computational cost,the SAFE strategy utilises a series of EMs with different accuracies and costs to collaboratively accomplish the entire evolutionary process.Hence, in this part,we study the influence of different series of EMs for SAFE-PSO.Four series of EMs are designed,which are shown in Table 4.In detail,the first series is to design EM1,EM2,and EM3with 5,10,and 15 epochs respectively,denoted as SAFEI.The second series is to design EM1,EM2,and EM3with 10,15,and 20 epochs respectively,denoted as SAFE-II.The third series is to design EM1, EM2, and EM3with 5, 15, and 25 epochs respectively, denoted as SAFE-III.While the fourth series is to design EM1, EM2, and EM3with 10, 20, and 30 epochs respectively, denoted as SAFE-IV.Moreover, each series is run three times on the single Nvidia 3090 GPU card and the best results are reported.Herein,the SAFE-III is actual the SAFE-PSO used in the above experiments, while other SAFE variants mean that we set the different number of epochs to other values.
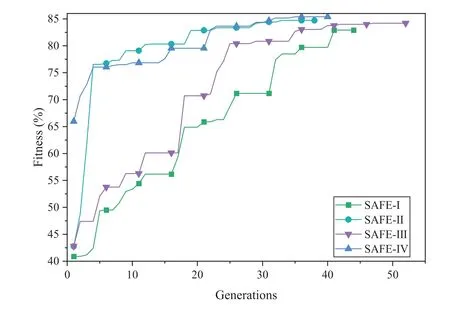
The comparison results of four series of EMs are shown in Table 5.SAFE-III obtains the highest accuracy among all runs of four series on CIFAR10.Although the accuracy obtained by SAFE-I is slightly higher than SAFE-III on CIFAR100, the number of parameters of the NN found by SAFE-III is smaller.Hence, we recommend using SAFE-III.However, iffewer computational cost is preferred, we recommend adopting the SAFE-I.Moreover,we draw the evolutionary curves in Figure 6, where they-axis represents the fitness value of theGbestin every generation obtained via Algorithm 1.The evolutionary curves show that the SAFE-I and SAFE-III both search for more candidate NNs and are not easy to stagnate,while SAFE-II and SAFE-IV are relatively easier to fall into a stagnant state, which shows that low-precision EMs have better exploration ability and high-precision EMs can further find the NN with better performance.
T A B L E 4 The training epochs setting of four different SAFE variants
F I G U R E 5 Evolutionary curves of the scale-adaptive fitness evaluation-based particle swarm optimisation (SAFE-PSO) algorithm with and without the SAFE strategy, where the y-axis represents the fitness value of the Gbest in every generation obtained via Algorithm 1
4.7 | Influence of the switch condition
In the stagnation-based switch strategy, maximal consecutive stagnation generationsSis the switch condition between EMs.Hence,Sdetermines whether the EM switch is carried out at the appropriate evolution stage.Therefore, we study the influence of differentSvalues on the performance of the SAFE-PSO algorithm.The SAFE-PSO usingS= 5 is compared with its variants usingS= 3,S= 7,S= 9, andS= 11.Same as the above experiment, each of them is run three times on a single Nvidia 3090 GPU card and the best results are reported.
The results are shown in Figure 7,where the bar represents the parameters and the line represents the classificationaccuracy of final NNs.We can see that the SAFE-PSO usingS= 5 and its variants usingS= 7 andS= 9 obtain similar performance on CIFAR10, which are better than the variants usingS=3 andS=11.That may be because neither too early nor too late to switch EMs with smallSor largeSin the evolution process is not suitable.Moreover, although the SAFE-PSO algorithm usingS= 3 orS= 7 performs much better than SAFE-PSO usingS=5 on CIFAR100,the number of parameters of the SAFEPSO-CNN obtained by SAFE-PSO usingS=5 is much less than those of the two variants.So,to sum up the above analysis, we recommend usingS= 5 as maximal consecutive stagnation generations.
T A B L E 5 The comparison of four different SAFE variants
5 | CONCLUSION
In this paper, we are committed to solving two major challenges of searching for the optimal NN automatically (i.e.,the difficulties of considering both hyperparameters and architectures, and the expensive computational cost in fitness evaluation), and propose the light-weight SAFE-PSO algorithm for optimising the HAO problem effectively and efficiently.Specifically, different from only optimising the architecture of NNs, we search for optimal hyperparameters and architectures jointly, which is more difficult with a more complex search space.Then, considering that the evaluation process of HAO requires expensive computational time and computational resources, we design the novel SAFE strategy and the stagnation-based switch strategy, which are integrated into PSO to form the complete SAFE-PSO.The experimental results show that the SAFE-PSO algorithm can obtain promising results, and the SAFE strategy can improve the search ability of the SAFE-PSO algorithm.Moreover, the obtained SAFEPSO-CNN based on the subset of CIFAR10 can directly apply to the CIFAR100 and performs quite well,which indicates that our SAFEPSO-CNN has a good transferability.
F I G U R E 6 Evolutionary curves of the algorithms with four different SAFE variants, where the y-axis represents the fitness value of the Gbest in every generation obtained via Algorithm 1

F I G U R E 7 Comparing the classification accuracy and number of parameters of the SAFEPSO-CNN obtained by the scale-adaptive fitness evaluationbased particle swarm optimisation(SAFE-PSO)algorithm with different maximal consecutive stagnation generations S on CIFAR10 and CIFAR100,where the bar represents the classification accuracy and the line represents the number of parameters
In fact, besides the serious issue of computational cost,HAO has many other challenges that need to be addressed in the future.For example, when considering both architectures and hyperparameters, how to design the encoding scheme to better represent the NN is still a challenge.Moreover, how to design a search space with more possible high-performance NNs is another challenge.In future work, with the help of the efficient SAFE strategy, we can address these challenges with light computational cost.In addition, techniques for solving EOP (e.g., distributed computational methods [61–64]and surrogate-assisted models [65, 66]) will be studied to further enhance the SAFE-PSO algorithm.
ACKNOWLEDGEMENTS
This work was supported in part by the National Key Research and Development Program of China under Grant 2019YFB2102102, in part by the National Natural Science Foundations of China under Grant 62176094 and Grant 61873097,in part by the Key-Area Research and Development of Guangdong Province under Grant 2020B010166002,in part by the Guangdong Natural Science Foundation Research Team under Grant 2018B030312003,and in part by the Guangdong-Hong Kong Joint Innovation Platform under Grant 2018B050502006.
CONFLICT OF INTEREST
No.
DATA AVAILABILITY STATEMENT
Data that support the findings of this study are available from the corresponding author upon reasonable request.
ORCID
Zhi-Hui Zhanhttps://orcid.org/0000-0003-0862-0514
 CAAI Transactions on Intelligence Technology2023年3期
CAAI Transactions on Intelligence Technology2023年3期
- CAAI Transactions on Intelligence Technology的其它文章
- Fault diagnosis of rolling bearings with noise signal based on modified kernel principal component analysis and DC-ResNet
- Anti‐noise diesel engine misfire diagnosis using a multi‐scale CNN‐LSTM neural network with denoising module
- Iteration dependent interval based open‐closed‐loop iterative learning control for time varying systems with vector relative degree
- Thermoelectric energy harvesting for internet of things devices using machine learning: A review
- An embedded vertical‐federated feature selection algorithm based on particle swarm optimisation
- An activated variable parameter gradient-based neural network for time-variant constrained quadratic programming and its applications
