Kernel extreme learning machine‐based general solution to forward kinematics of parallel robots
Jun Ma| Xuechao Duan | Dan Zhang
1Key Laboratory of Electronic Equipment Structure Design of Ministry of Education,Xidian University,Xi'an,Shaanxi, China
2Lassonde School of Engineering, York University,Toronto,Ontario, Canada
Abstract The forward kinematics of parallel robots is a challenging issue due to its highly coupled non-linear relation among branch chains.This paper presents a novel approach to forward kinematics of parallel robots based on kernel extreme learning machine (KELM).To tackle with the forward kinematics solution of fully parallel robots, the forward kinematics solution of parallel robots is equivalently transformed into a machine learning model first.On this basis, a computational model combining sparrow search algorithm and KELM is then established, which can serve as both regression and classification.Based on SSA-optimised KELM (SSA-KELM) established in this study, a binary discriminator for judging the existence of the forward kinematics solution and a multilabel regression model for predicting the forward kinematics solution are built to obtain the forward kinematics general solution of parallel robots with different structural configurations and parameters.To evaluate the proposed model,a numerical case on this dataset collected by the inverse kinematics model of a typical 6-DOF parallel robot is conducted, followed by the results manifesting that the binary discriminator with the discriminant accuracy of 88.50%is superior over ELM,KELM,support vector machine and logistic regression.The multi-label regression model, with the root mean squared error of 0.06 mm for the position and 0.15°for the orientation,outperforms the doublehidden-layer back propagation (2-BP), ELM, KELM and genetic algorithm-optimised KELM.Furthermore, numerical cases of parallel robots with different structural configurations and parameters are compared with state-of-the-art models.Moreover, these results of numerical simulation and experiment on the host computer demonstrate that the proposed model displays its high precision, high robustness and rapid convergence,which provides a candidate for the forward kinematics of parallel robots.
K E Y W O R D S artificial intelligence, classification, machine learning, regression analysis, robotics
1 | INTRODUCTION

F I G U R E 1 The application of the forward kinematics of parallel robots: (a) feedback control and (b) calibration.
Parallel robots, in comparison with their serial counterpart,offer intrinsic advantages of high precision, high stiffness and high loading capability [1], therefore, they have been extensively applied and brought breakthroughs in numerous fields such as the motion generator [2], parallel machine tools [3–5],antenna mount [6], sensors [7], manufacturing [8, 9] and rehabilitation exercises [10–12].The motion-planning and control problem play crucial roles in the field of robotics regardless of serial robots or parallel robots [13–15].With the further research of parallel robots, it is necessary to cope with the forward kinematics of parallel robots for their feedback control (as shown in Figure 1a) [16], workspace, calibration(Figure 1b) [17, 18] and many other potential applications.However,the forward kinematics solution of parallel robots is generally complicated since it results in an underdetermined solution because of its highly coupled non-linear equations which are difficult to obtain its analytic solution [19].According to the existing literature review, the approaches currently dealing with the aforementioned problem can be divided into four categories: analytical approaches [20] numerical methods [19, 21] extra-sensor approaches [22] and artificial intelligence methods [23, 24].For example, seven methods for solving the forward kinematics of redundant hybrid parallel robots based on the extra actuator encoders were proposed by Wen et al.[25].Ghaedrahmati et al.[26]studied the forward kinematic models of 2-degree-of-freedom(DOF) parallel wrist by adopting a geometrical approach.In addition, a mathematical toolkit of the absolute nodal coordinate was introduced to solve the positioning of the soft parallel robots [27].An analytical approach applying the Denavit–Hartenberg (D-H) notation to the forward kinematics of the 3–6 Stewart platform was proposed by Shim et al.[28], but it was not intended to improve the speed or precision of the endeffector.Nevertheless, it is of crucial significance to calculate the forward kinematics of parallel robots in real-time control.The computational cost of some algorithms for solving the forward kinematics of parallel robots is high, and a set of forward kinematics solution information can only be obtained within a period of 0.5 s [29].
In view of the current existing theoretical research results,artificial neural network (ANN), as an alternative approach to the forward kinematics solution of parallel robots, is superior to other methods in terms of computational efficiency and accuracy [30].For instance, the BP neural network model optimised by GA was used by Liu et al.[31] to address the forward kinematics problems of Delta parallel robot.Alternatively, Nguyen and Caverly [32] introduced two extended Kalman filtering algorithms integrating payload accelerometer and rate gyroscope data with the forward kinematics to estimate the pose of the cable-driven parallel robot.Meanwhile,Zhang et al.[33] reported the kinematic calibration method with an average position error of 0.4 mm for cable-driven parallel robots (CDPR) considering the pulley mechanisms kinematics.Besides, an adaptive neuro-fuzzy inference structure model was utilised by Azar et al.[34]to attain the forward kinematics solution of the 3-DOF planar parallel robot.A basic neural network model proposed by Prado et al.[30] was used to address the forward kinematics of a wearable 3-RRS(R, S, P, U corresponding to revolute joint, spherical joint,prismatic joint, universal joint, respectively) parallel robot.Similarly, Mohammad et al.[35] presented a neural network model with external forces to estimate the position of the cable-driven parallel robot, whose network error was acquired at approximately 0.38% for positions and 3.87% for angles.The ANN based on wavelet neural network(ANN-WNN)was developed by Rahmani and Ghanbari [36] to tackle with the forward kinematics of the dual-layer-6UPS (2-(6UPS)) parallel robot.Three BP neural network optimisation algorithms were adopted by Zhang et al.[37]to solve the forward kinematics of the 2RPU-2SPR parallel manipulator for the manufacture of large heterogeneous complex structural parts in the aerospace field.In addition, Noppeney et al.[38] proposed a method,with an average estimation error of<0.5 mm,combining dual quaternion algebra and a neural network for the forward kinematics of a Delta robot.The neural network Newton–Raphson iterative algorithm was utilised by Zhang et al.[39]to solve the forward kinematics of 2RPU-2SPR parallel robot.Likewise, López et al.[1] presented the neuro-genetic algorithm to estimate the problems of the maximum workspace and the forward kinematics concerning the Stewart platform.To get a suitable moving-platform posture for given lengths of the limbs, the neural network formulation led by an unsupervised iterative technique was designed by Mishra and Caro[40,41].The multilayer perceptron studied by Zare et al.[42] aims to solve the forward kinematics of the CDPR,which possesses a mean average error of about 2 mm for the position and 0.78°for the orientation in dimensions of 360×220×160 cm.The approach [43], with maximum errors of 10-4mm and 10-2degrees for the translational and rotational motions, respectively,used an integration of the error correcting output codes algorithm and the neural network, which was presented by Tavassolian to solve the forward kinematics of a 3-PRR planer parallel robot.A quantum genetic algorithm-based improved BP neural network was developed by Chen to solve the forward kinematics of the Stewart parallel platform[44].Similarly,a multi-layer feed-forward neural network was trained after using different metaheuristic optimisers to solve the forward kinematics of the Stewart platform [45].
To summarise, although ANN is a more suitable technology to address the forward kinematics problem of parallel robots, there still exists the following drawbacks: (1) Few scholars have yet presented a general framework of forward kinematics for parallel robots with different structural configurations and parameters.(2) The accuracy of the forward kinematics solution regarding parallel robots needs to be improved by advanced optimisation algorithms instead of sheer ANNs,which are rarely employed in previous researches.(3) An ANN model must have the output as long as there exists an input; however, there exists little practical physical significance for parallel robots because of the strong coupling among the branch chains.This paper mainly investigates the forward kinematics general solution of parallel robots and manages to make improvements for the above-mentioned shortcomings.
The remaining parts of this paper are organised as follows.Firstly, comparison of the inverse and forward kinematics models of parallel robots and dataset collection method are introduced in Section 2,followed by the proposed approaches are presented in Section 3.Then, the results of the implemented numerical cases are described and analysed in Section 4.Finally, these contributions of this paper are briefly concluded in Section 5.
2 | INVERSE AND FORWARD KINEMATICS MODELS
The inverse kinematics model of parallel robots is used to obtain the training and testing datasets of the neural network,and the comparison between the inverse and forward kinematics of parallel robots is then made.
The inverse kinematics of parallel mechanism is to solve the lengths or angles of each branch chain with the known position and orientation of the end-effector.On the contrary,the displacement forward kinematics of the parallel mechanism is to solve the position and orientation of the end-effector according to the known lengths or angles of each branch chain.A comparison relation of the inverse and forward kinematics of parallel robots is shown in Figure 2.
3 | MODEL CONSTRUCTION
In this section, the related work consisting of kernel extreme learning machine(KELM)and sparrow search algorithm(SSA)are described, followed by the procedures of the SSA-KELM model for the forward kinematics of parallel mechanisms are illustrated.In addition, the SSA-KELM-based binary discriminator and multi-label regression model are established.
3.1 | Kernel extreme learning machine
ELM was originally proposed by Huang et al.[46]in 2006 and has been successfully applied in many fields [47] owing to the advantages of better convergence and generalisation performance.In 2012,KELM[48]integrated with regularisation and kernel matrix to ELM for regression and multiclass classification was also designed by Huang.

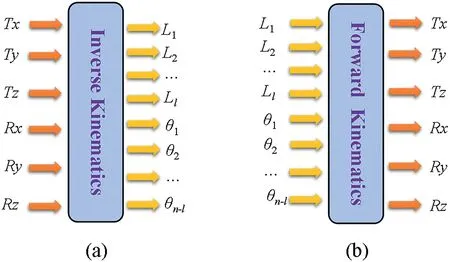
F I G U R E 2 Inverse and forward kinematics models: (a) inverse and(b) forward.The inputs include two forms of length and angle, hence suppose there are l lengths forms and n inputs.

3.2 | Sparrow search algorithm
SSA is a novel swarm intelligence optimisation approach proposed by Xue and Shen [49] in 2020, which is inspired by foraging and anti-predation behaviours of sparrows and being superior over grey wolf optimiser,particle swarm optimisation and gravitational search algorithm.The SSA is composed of three parts: discoverer, follower and investigator, whose updated rules are formulated as follows.
The location of the discoverer is altered by

where,Xbtis the current global best location value at iterationt,μis a random number obeying normal distribution,κ∈[-1,1]is a rand number andεis a number close to zero for avoiding zero division error.The current global maximum and minimum fitness values arefbandfw, respectively.
3.3 | Construction of overall framework
The forward kinematics solution of parallel robots is to obtain the position and orientation of the end-effector given the inputs (i.e.the length or angle of input joints) of each branch chain.Consequently, the forward kinematics solution problem of parallel robots can be regarded as a neural network architecture with multi-input and multi-label.Correspondingly, the SSA-KELM-based multi-label regression model for predicting the forward kinematics solution of parallel robots and the SSAKELM-based binary discriminator for judging the existence of the forward kinematics to avoid the defect that an ANN model must have the output as long as there is an input are established respectively, as shown in Figure 3.Moreover, the calculation procedures of the proposed model are shown in Figure 4.
The process flow of the proposed general framework described in Figures 3 and 4 can be summarised in the following major steps.
Step1 Collecting data from the inverse kinematics of the parallel robot.
Step2 Judging the existence of the forward kinematics solution by SSA-KELM-based binary discriminator.
Step3 Predicting that the forward kinematics solution are built to obtain the forward kinematics by SSA-KELM-based multilabel regressor.
3.3.1 | Binary discriminator
Specifically, the SSA-KELM-based binary discriminator, as a model for judging the existence of the forward kinematics solution, is initially set up, which can be regarded as an early alert mechanism if there does not exist the forward kinematics solution for the parallel robot.In this study,1 and -1 express the forward kinematics with and without solution,respectively.Currently, the relevant literature [50] only used the signum function for converting the regression return value to categories, that is, its segmentation threshold is zero, as shown in the following formulation where the classification performance is not the best because the selected segmentation threshold is not the optimal.
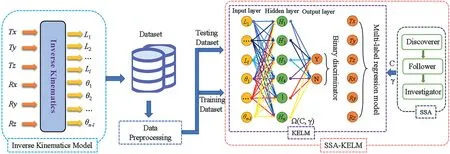
F I G U R E 3 schematic diagram of the proposed model.
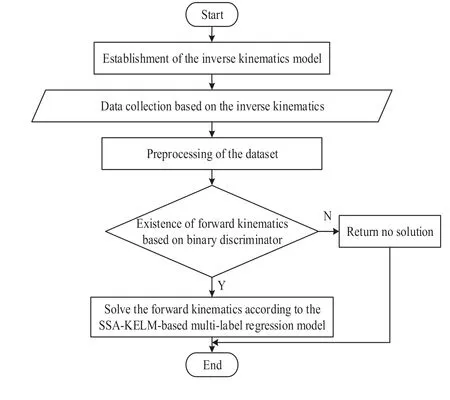
F I G U R E 4 Flowchart of the model.
where,Yρis the predicted regression value of the category.
In this study,the optimisation algorithm SSA mentioned in the previous section is used to select the best segmentation thresholdτ, and the threshold discriminant function is defined as
Simultaneously, to comprehensively evaluate the performance of the proposed SSA-KELM-based binary classification model, the following evaluation metrics are defined in Figure 5.
Theoretically speaking, higherRandPvalues represent better classification performance of the algorithm.However,in practice,bothRandPvalues are mutually exclusive.Therefore,in this sense, the values ofRandPneed to be controlled by certain constraint variables, such asF-Score obtained by weighted harmonic mean as shown below.
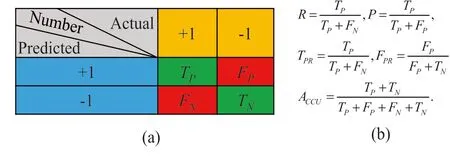
F I G U R E 5 Metrics of evaluation: (a) confusion matrix and(b)definitions of evaluation metrics.R,P,TPR,FPR and ACCU denote recall rate, precision rate, true positive rate (TPR), false positive rate (FPR) and accuracy rate (ACCU), respectively.
A higherF-score value indicates a better classification performance.Since bothRandPare equally important,letα=1.Thereby the objective function of theF-score can be set as
whereτ∈[-1,1] represents the segmentation threshold for regression values.
In addition, the receiver operating characteristic (ROC)curve and precision-recall (PR) curve can excellently present the classification performance for binary discriminant problems in the case of unbalanced numbers between positive and negative samples.
3.3.2 | Multi-label regression model
An unconstrained optimisation model for minimising root mean squared error (RMSE) by optimising the hyperparameters of KELM is then constructed.The units of position and orientation of the parallel robot are inconsistent, and the RMSE of the orientation is more sensitive than that of the position.Accordingly, the weighted sum optimisation model scalarising the RMSE of positionf1and orientationf2bi-objective into a single objectiveFby adding objective and pre-multiplied by a weight ofw1=0.4 andw2=0.6,respectively is defined as
Afterwards, RMSE for the translational and rotational motions of the end-effector can be formulated as
where,ψo(hù)andψpdenote the observed and predicted value,respectively, and ? is the number of samples.
Based on SSA and KELM, the proposed multi-label regression model for the forward kinematics solution of parallel robots is summarised in detail as the pseudo code shown in Algorithm 1.

Al gorithm 1 The framework of the SSA-KELM Input: M, SN, LB, UB, F.M: the maximum iterations of SSA.PN: the number of discoverers.SN: the number of search agents of SSA.DN: the number of investigators.LB: the lower bound of the regularisation factor and kernel parameter.UB: the upper bound of the regularisation factor and kernel parameter.Output: Xb, fb.In the discriminator,Xb contains C,γ and τ;In the regressor, Xb contains C and γ.1: F is obtained by the function of KELM in Equation (12).2: while (it < M)3: R2 = r and (1)4: for k ←1 to PN do 5: Update the location of the discoverer with Equation (5).6: end for 7: for k ←(PN + 1) to SN do 8: Update the location of the follower with Equation (6).9: end for 10: for k2 ←1 to DN do 11: Update the location of the investigator with Equation (7).12: end for 13: it ←it + 1 14: end while 15: return Xb, fb.
4 | SIMULATED RESULTS AND ANALYSIS
4.1 | Data collection
In this section,the Stewart platform,as the most representative parallel robot,is chosen as a study case.As shown in Figure 6,the Stewart platform consists of six identical electric-cylinder actuators and basic and top platforms.Each electric-cylinder actuator contains two parts connected with a prismatic joint and interconnects the basic platform to the top platform by spherical joints atBiandTi,i= 1, 2, …, 6.
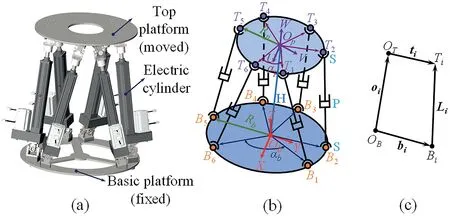
F I G U R E 6 Kinematic analysis of the Stewart platform: (a) Threedimensional model, (b) mechanism diagram and (c) closed-loop vector illustration of single branch chain.
In Figure 6b,each branch of the Stewart platform and the centre of the basic and top platforms form a closed-loop like in Figure 6c.RbandRprepresent the radius of the basic and top platforms, respectively.αbandαpmean large adjacent angle between spherical joints and small adjacent angle between spherical joints, respectively.For ease of calculation,ObXYZandOpUVWare established as the global coordinate system and the local coordinate system, respectively.The centreline betweenB1ObandB6Obon the basic platform is taken as theX-axis, and the vertically upward direction of the basic platform is set as theZ-axis in the global coordinate system ofObXYZ, similarlyOpUWV.Consequently, the coordinates of six points in the basic platform can be obtained according to the transformation of the coordinates, which is similar to the coordinates of each point in the top platform.
Next, it is assumed that the coordinate systemOpUWVrotates around theX,YandZaxes in the global coordinate system ofObXYZby anglesγ,βandα,successively.Thus,the overall pose transformation matrix of the coordinate systemObXYZis obtained by
wherecandsexpress trigonometric functions cosine and sine,respectively.
In practice, the order of rotation around a fixed angle is different,and different combinations can be obtained from the above formula to collect the dataset.In addition, after fixed angle rotation, Euler angles rotation can be performed if necessary.Suppose it rotates aboutZ′,Y′andX′axes with anglesα′,β′andγ′, successively, hence the rotation matrix of the end-effector can be calculated as
LetLBiTi=Li,i=1,2,…,6 and then it can obtain the branch chain vectorLifrom the closed-loop vector relation in Figure 6c as follows.

The dataset for model training and testing can be obtained by setting the position and orientation to determine the length of each branch.Besides, the forward kinematics model of parallel robots can also be obtained for the height difference among the pointsBiandTi, which reflects the robustness of the method proposed in this study.
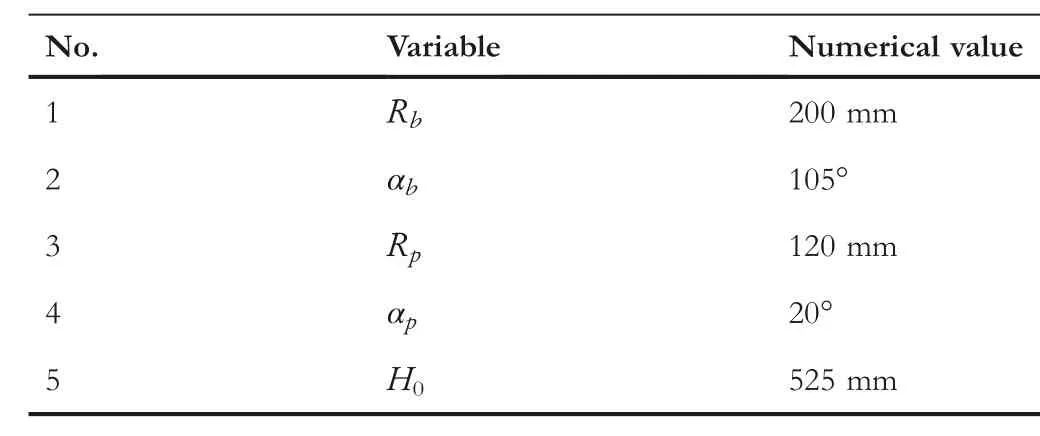
Then, the structural parameters referred to Figure 6 are listed in Table 1.According to the inverse kinematics model of the Stewart platform, the length of each branch chain for the given structural parameters is calculated.In the process of data collection,the parallel computation pool with 12 cores is used to speed up the execution of the programme.
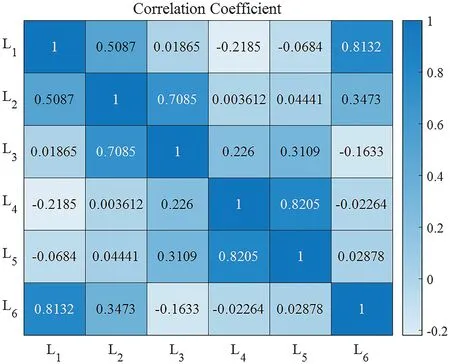
Moreover, Pearson correlation coefficients are shown in Figure 7.From Figure 7, it can be concluded that there is a strong correlation betweenL1andL6,L2andL3,L4andL5,which is the same as the structural characteristic.Moreover,dimensionality reduction processing is unnecessary since the correlation coefficients are not very large.
Based on the collected dataset, the dataset with respect to the binary discriminator is extracted by adding random generation errors to branch lengths for generating negative labels.
4.2 | Data preprocessing
The data preprocessing is mainly divided into order shuffling and normalisation to improve the approximation and generalisation ability of the model of which specific procedures are listed as follows.
Step1 A new dataset is generated by selecting random number sequences.Step2 The dimensionless processing of the dataset is required since the units of branch length and position are millimetres and the unit of the end-effector orientation is the degree.The normalisation model processes matrices by normalising the minimum and maximum values of each sample to [-1, 1],which is calculated as
T A B L E 1 Structural parameters of the Stewart platform
wheredis the sample vector of the collected data,anddminanddmaxare the minimum and maximum feature values of the sample vector in the attributes, respectively.
4.3 | Binary discriminator
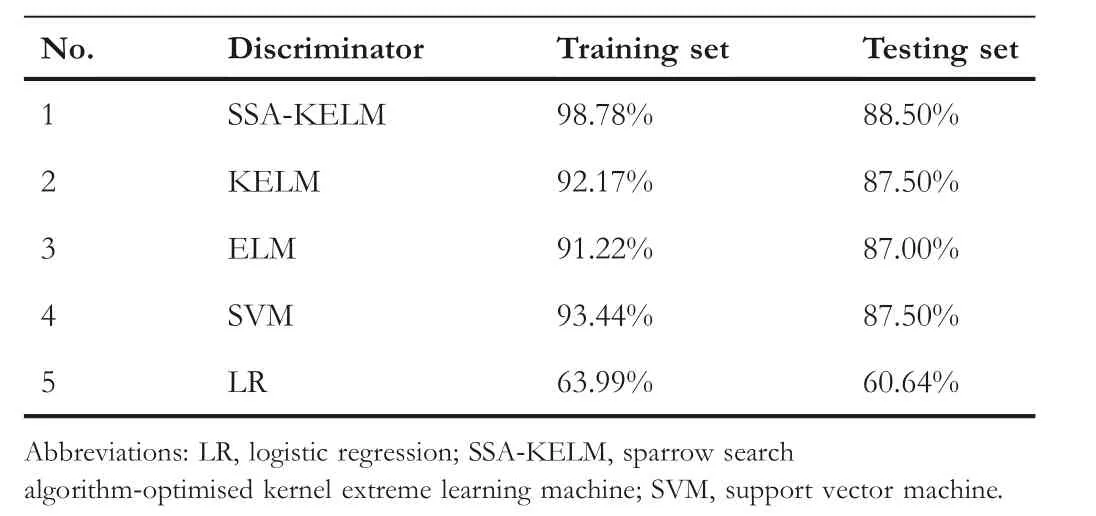
The collected dataset is tested on the SSA-KELM-based binary discriminator.The discriminant accuracy results of the proposed SSA-KELM-based binary discriminator and other binary classifiers are listed in Table 2,among which the proposed binary discriminator is proved to be the optimal with the accuracy of 98.78% for the training set and 88.50% for the testing set.
F I G U R E 7 Pearson correlation coefficient table.
T A B L E 2 Comparison of several discriminators in classification accuracy
To further explore the superiority of the above-mentioned SSA-KELM-based binary discriminator, ROC curves and PR curves are drawn in Figures 8 and 9, respectively.Some parameter values in Algorithm 1 are initialised:M= 100,SN= 20,LB= [30, 0.1, -1] andUB= [1000, 1, 1].In ROC curves,AUC refers to the area enclosed by the coordinate axes under the ROC curve,and the closer AUC is to 1.0,the higher the authenticity of the detection method.In ROC curves and PR curves,the best goal is to be in the upper left-hand corner and upper right-hand corner,which means that the smaller the false positive rate and the larger the true positive rate,and the larger theRand the larger theP,the better the performance of the algorithm.Accordingly, the discriminative ability and effectiveness of the proposed SSA-KELM-based binary discriminator are stronger than those of other classifiers.
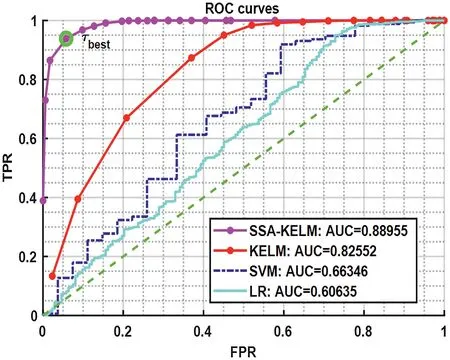
F I G U R E 8 Comparison of different model in ROC space.ROC,receiver operating characteristic.
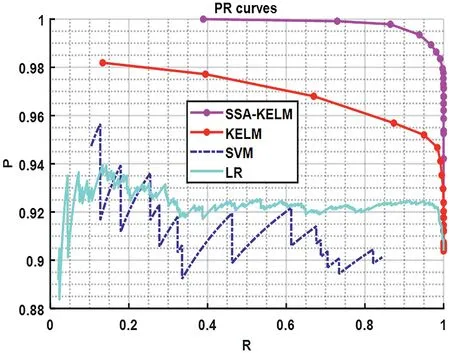
F I G U R E 9 Comparison of different model in PR space.PR,precision-recall.
4.4 | Multi‐label regression model
The dataset collected by the inverse kinematics model of the Stewart platform is implemented on the established SSAKELM-based multi-label regression model.Firstly, the parameters of Algorithm 1 are set as:M= 100,SN= 20,LB= [30, 0.1] andUB= [1000, 1].The iterative evolution curves of SSA-KELM and genetic algorithm-optimised KELM(GA-KELM) are shown in Figure 10.It can be concluded from Figure 10 that the optimal RMSE value of SSA-KELM is smaller than that of GA-KELM.
In the following, cumulative distribution function graphs of KELM and SSA-KELM are given in Figures 11 and 12,respectively, to describe the probability distribution of the absolute errors about the objective function, which indicate that the RMSE of SSA-KELM-based multi-label regression model are comparatively smaller than that of KELM.Additionally, in Figure 12, the absolute errors of the objective function regarding the SSA-KELM multi-label model are distributed between zero and 0.9 with 0.2 at 90%, which illustrates the effectiveness and predictability of the proposed SSA-KELM prediction model.Relatively,the RMSE ofRxandRzare larger in comparison to those ofTx,Ty,TzandRz,which implies the characteristics concerning parallel mechanisms that rotational motions exceptRzare more sensitive than translational motions.The reason for this is that rotational motions except forRzresult in both an increase and decrease in the lengths of branch chains, while translational motions lead to only an increase or decrease in the lengths of branch chains.
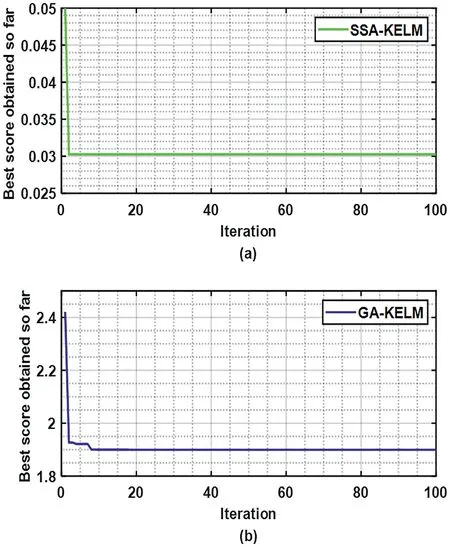
F I G U R E 1 0 Objective space of SSA-KELM and GA-KELM.(a) SSA-KELM; (b) GA-KELM.GA-KELM, genetic algorithm-optimised kernel extreme learning machine; SSA-KELM, sparrow search algorithmoptimised kernel extreme learning machine.
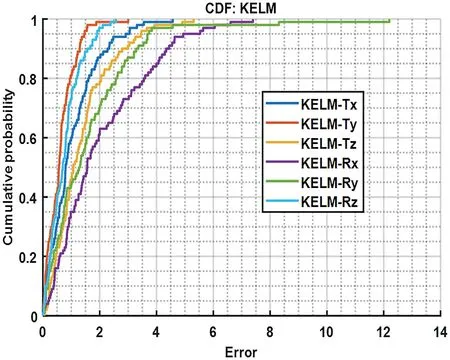
F I G U R E 1 1 CDF distribution of KELM.CDF, cumulative distribution function; KELM, kernel extreme learning machine.
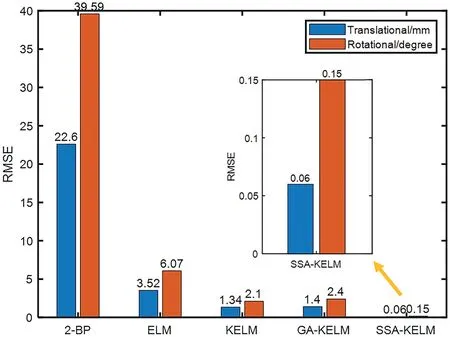
F I G U R E 1 3 Error comparison of five methods in accuracy.
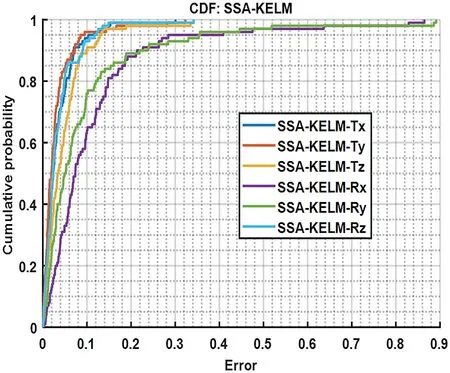
F I G U R E 1 2 CDF distribution of SSA-KELM.CDF, cumulative distribution function; SSA-KELM, sparrow search algorithm-optimised kernel extreme learning machine.
The RMSE of position and orientation on the training set are 0.0211 mm and 0.0363°, respectively, and the RMSE of position and orientation on the testing set are 0.0623 mm and 0.1509°, respectively.As depicted in Figure 13, a comparison of the SSA-KELM model with other prediction methods,including 2-BP, ELM, KELM and GA-KELM, is made in the optimal value of the objective function,which explains that the proposed SSA-KELM multi-label model outperforms other prediction algorithms.
4.5 | Comparing with state‐of‐the‐art models
In order to more deeply demonstrate the strong generalisation ability and effectiveness of SSA-KELM method proposed in this study, a comparison of the established SSAKELM-based multi-label regression model with several prior state-of-art models in the same structural configurations and parameters are tabulated in Table 3.According to the previous rigorous numerical comparison in Table 3, it can be concluded that the proposed SSA-KELM method possesses higher accuracy compared thanthe current state-of-the-art models.
4.6 | Experiment
In order to evaluate the real-time response performance of the method proposed in this paper, experiments on the host computer with Visual C-integrated developing environment are carried out.The experimental system mainly includes the Stewart platform, servo drivers,controller and host computer,as shown in Figure 14.
The C programing language is developed on the host computer with Intel Core i5-5200U CPU, whose average consumed time of each set is 6 ms (The specific programme running time is shown in Table 4.), indicating that the proposed algorithm has a high response in solving the forward kinematics solution of parallel robots.
5 | CONCLUSIONS
This research aims to construct a multi-label regression model and binary classification model for the forward kinematics general solution of parallel robots with different structural configurations and parameters in high precision.The main contributions of this article can be summarised as follows:
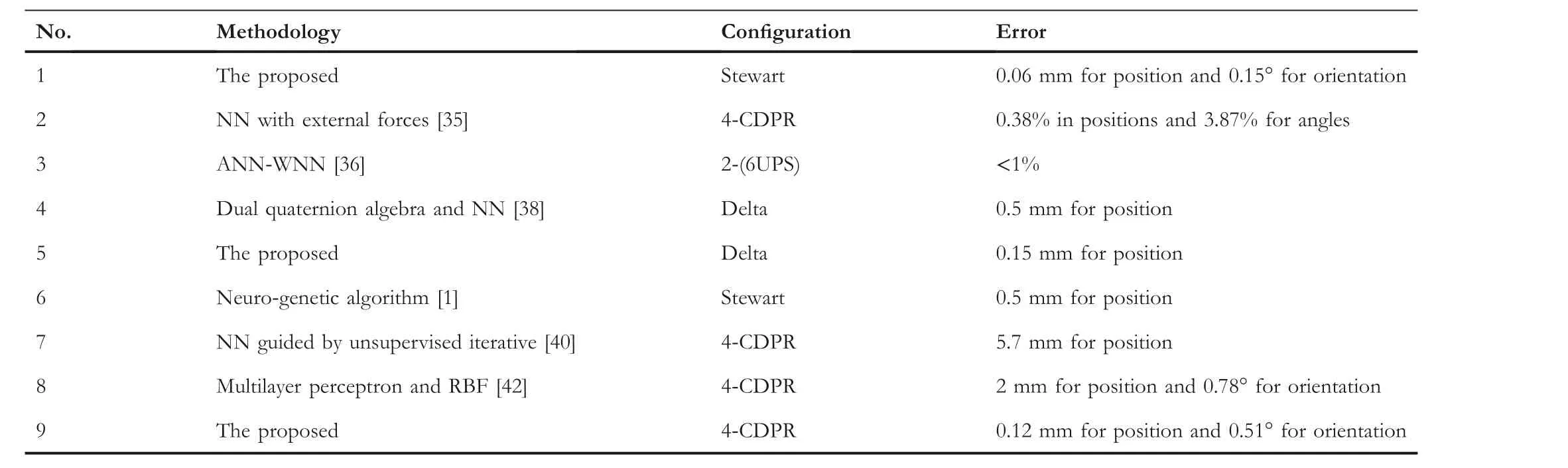
T A B L E 3 Comparison with state-of-the-art models
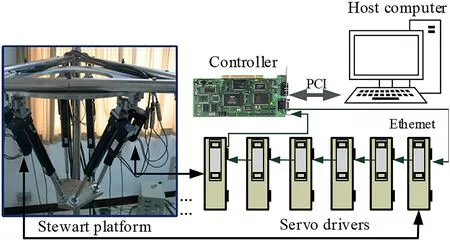
F I G U R E 1 4 The block diagram of the experimental system.
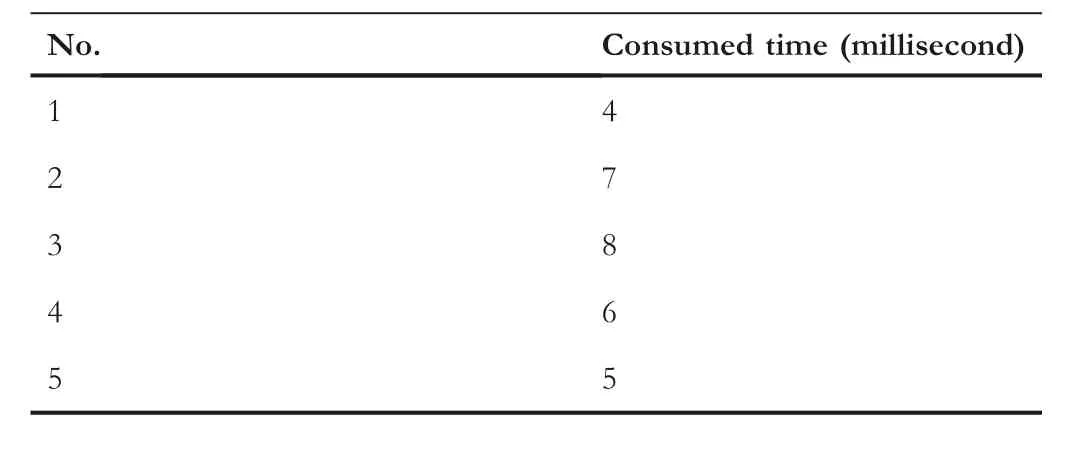
T A B L E 4 Five groups of programs running time
(1) A general framework for the forward kinematics solution of parallel robots is first proposed based on KELM optimised by SSA.The proposed SSA-KELM algorithm can be implemented both for regression and classification by switching the segmentation function.In addition, SSA is applied to serve as the optimisation of the hyperparameters in which KELM and segmentation are threshold discriminant functions.
(2) The SSA-KELM-based binary discriminator and multilabel regression model are comprehensively developed to accurately distinguish the existence of the forward kinematics solution and solve the forward kinematics of parallel robots, respectively, which can be extensively applied to parallel robots with different structural configurations and parameters.
(3) The generalisation performance and effectiveness of the established SSA-KELM are verified by the numerical simulations on the different parallel robots and are compared with other algorithms.The results show that the RMSE of position and orientation on the testing set are 0.06 mm and 0.15°,respectively,which outperforms other algorithms and makes a case for precise forward kinematics of parallel robots.The feasibility and validity of the proposed general framework which can be applicable to any structure of parallel robots are demonstrated from the analytical results.Consequently, extensive simulations indicated that the framework proposed in this paper has high generality and generalisation in solving the forward kinematics of parallel robots.Correspondingly, the proposed general framework provides strong support conditions for real-time control, calibration and output error analysis of parallel robots.In the future work,the proposed model will be conducted on a parallel physical experiment platform with higher precision to output the position and orientation of the end-effector in real-time by inputting the known lengths or angles of each branch chain, and its generalisation performance needs to be improved.
ACKNOWLEDGEMENTS
This work is supported by National Natural Science Foundation of China under Grant No.52175246, ‘111 project’ under Grant No.B14042 and Natural Science Basic Research Plan in Shaanxi Province of China under Grant 2021JM-122.Another,thanks to Jiaming Xiao and Huansi Sun for their help with the experiment.
CONFLICT OF INTEREST
The authors declared no potential conflicts of interest with respect to the research, authorship, and publication of this article.
DATA AVAILABILITY STATEMENT
Research data are not shared.
ORCID
Jun Mahttps://orcid.org/0000-0002-1814-6484
 CAAI Transactions on Intelligence Technology2023年3期
CAAI Transactions on Intelligence Technology2023年3期
- CAAI Transactions on Intelligence Technology的其它文章
- Fault diagnosis of rolling bearings with noise signal based on modified kernel principal component analysis and DC-ResNet
- Leveraging hierarchical semantic‐emotional memory in emotional conversation generation
- Forecasting patient demand at urgent care clinics using explainable machine learning
- A federated learning scheme meets dynamic differential privacy
- SRAFE: Siamese Regression Aesthetic Fusion Evaluation for Chinese Calligraphic Copy
- Wafer map defect patterns classification based on a lightweight network and data augmentation
