Recursive recurrent neural network: A novel model for manipulator control with different levels of physical constraints
Zhan Li| Shuai Li
1Department of Computer Science, Swansea University,Swansea,UK
2College of Engineering,Swansea University,Swansea,UK
Abstract Manipulators actuate joints to let end effectors to perform precise path tracking tasks.Recurrent neural network which is described by dynamic models with parallel processing capability, is a powerful tool for kinematic control of manipulators.Due to physical limitations and actuation saturation of manipulator joints, the involvement of joint constraints for kinematic control of manipulators is essential and critical.However,current existing manipulator control methods based on recurrent neural networks mainly handle with limited levels of joint angular constraints,and to the best of our knowledge,methods for kinematic control of manipulators with higher order joint constraints based on recurrent neural networks are not yet reported.In this study,for the first time,a novel recursive recurrent network model is proposed to solve the kinematic control issue for manipulators with different levels of physical constraints, and the proposed recursive recurrent neural network can be formulated as a new manifold system to ensure control solution within all of the joint constraints in different orders.The theoretical analysis shows the stability and the purposed recursive recurrent neural network and its convergence to solution.Simulation results further demonstrate the effectiveness of the proposed method in end-effector path tracking control under different levels of joint constraints based on the Kuka manipulator system.Comparisons with other methods such as the pseudoinverse-based method and conventional recurrent neural network method substantiate the superiority of the proposed method.
K E Y W O R D S dynamic neural networks, recursive computation, robotic manipulator
1 | INTRODUCTION
Manipulators, which can greatly reduce the heavy burden on labour forces of workers, nowadays have been widely applied in many industrial fields such as welding, painting, and assembling areas.By using extra degrees of freedom (DOFs),manipulators are able to make use of inherent redundancy to perform flexible operations and fulfil complicated tasks [1, 2].Kinematic control of manipulators by taking advantage of such inherent redundancy in various circumstances have drawn intensive interests and concerns in recent years [3].
Generally, kinematic control of manipulators is to seek a suitable control action in the joint space that produces a desired motion for the end effector in the workspace.However, strong coupled non-linearity exists in the mapping between a joint space and a Cartesian workspace of a redundant manipulator when it executes manipulation tasks.It is difficult to tackle this problem for analytical solutions in the joint space level through directly solving the coupled non-linear equations that are used to describe the kinematic characteristics of manipulators.Therefore, the kinematic control problem in the joint space is converted into a problem depicted by the velocity kinematic equations.Some early research studies found the control solutions directly by solving the pseudoinverse of the Jacobian matrix of a manipulator [4, 5], and such a way of processing may increase local instability and even need more computational costs which were not expected.
To overcome the shortcomings of pseudoinverse-based approaches, optimisation-based (e.g.quadratic programming)methods have been proposed to find the optimal control solutions [6, 7].Such optimisation-based methods can involve physical constraints into the optimisation formulation [8] and solutions to such constrained optimisation problems cannot be obtained in an analytical manner as well.Thus, numerical methods in a way of serial processing were applied,but they are still resulting in low computational efficiency.In order to remedy this weakness, recurrent neural networks with parallel processing ability have been proposed for manipulator control[9–18].Many researchers have developed kinematics control paradigms with the involvement of one or two of the three levels of constraints: joint angle and joint velocity, and joint acceleration constraints.In ref.[19], joint limits and joint velocity limits are taken into account for the kinematic resolution based on a dual neural network.In ref.[20],automatic handling of kinematic constraints is proposed in a real-time operational space motion planner.In ref.[21],repetitive motion planning is performed with acceleration-level constraints.In ref.[22], kinematic control of manipulators with obstacle avoidance in the joint-acceleration level is proposed with a minimum acceleration norm as the optimisation objective.In ref.[23], kinematic control of the manipulators with joint velocity constraints is solved by a passivity-based approach from an energy perspective.In ref.[24], the velocity-level and acceleration-level redundancy resolution are combined to form a unified quadratic programming for joint torque optimisation.In ref.[25], visual serving control of manipulators with joint physical limits to ensure safety.In ref.[26], both velocity-level and acceleration-level constraints are integrated into the kinematic control of manipulators.However, for joint constraints in a higher level such as more than the fourth-order joint constraints, kinematic control methods based on recurrent neural networks have not yet been proposed and reported.
Motivated by the aforementioned points, as current kinematic control methods based on recurrent neural networks can only deal with joint angular velocity and joint acceleration constraints, in this study, we are making breakthroughs to propose a novel recursive recurrent neural network for kinematic control of manipulators with different levels of physical constraints, with high-order joint constraints considered.The contributions of this study are summarised as follows:
(1) To the best of our knowledge, this article is the first work to propose the kinematics control method for manipulators with different levels of physical constraints simultaneously.
(2) The proposed method is described by a novel recursive recurrent neural network model,and the theoretical results on the purposed recursive recurrent neural network show the stability in a manifold system perspective and its convergence to kinematic control solutions with aforementioned physical constraints.
(3) Simulation results with comparisons to the pseudoinversebased method and conventional recurrent neural network method on the Kuka manipulator system demonstrate the efficiency and superiority of the proposed method in kinematic control with different levels of physical constraints.
2 | PROBLEM FORMULATION
Let us consider the following velocity kinematics equation for manipulator control
whereJ∈Rm×ndenotes the Jacobian matrix of the manipulator,r∈Rmdenotes trajectory in the Cartesian space of the end effector, andθ∈Rndenotes the joint space variable.The end effector has to follow the desired pathrdto make the tracking errore=r-rdas small as possible with suitable control actions from the joint space of the manipulator.Due to the physical restrictions of joint actuation of the manipulator, generally, the joint variable usually has to follow the limits in the joint angle level, joint velocity level, joint acceleration level, and higher order levels as follows

2.1 | Convectional kinematic control of manipulator with joint constraints of lower levels
Note that, current existing works mainly focus on solving the kinematic control issue with the first two low levels of constraints for joint variables as follows:
The kinematic control solution for the manipulator with the joint angle and joint velocity constraints is depicted by the following constrained optimization problem

For solving the optimization problem above, according to the Karush-Kuhn-Tucker condition [27], one can construct a recurrent neural network solver as follows:
wherew∈Rndenotes the state variable of the recurrent neural network,?> 0 denotes the convergence parameter,andPΩ0(?) denotes the piecewise linear projection function array.
2.2 | Kinematic control of manipulator with joint constraints of higher levels
However, as we may know, the following kinematic control issue with additional higher levels of joint variable constraints is still not considered and investigated

This situation can be frequently encountered.For instance, in jerk operations, the manipulator needs to compute the time derivatives of the joint acceleration, which leads to the third-order term for the joint angular variable.To avoid unnecessary dynamic vibrating that is affected by large variations from joint acceleration, it would be very useful to limit the range of the fourth-order term for the joint angular variable.
Therefore the aforementioned original solver for the kinematic control of manipulator with lower order joint constraints
is not able to handle with additional higher order constraints and simultaneously fulfil the tracking control task for the end effector, because the higher order constraint information cannot be involved in current recurrent neural network model.
As the lower order time derivative of joint variables can be obtained through the integration of the higher order time derivative of joint variables, in this paper, we try to solve the kinematic control issue by letting the higher order joint target firstly tracked and then lower order joint target tracked by the recurrent neural network solver.Under these considerations,we let the higher order time derivative of the state variablewfollow
and we getw(n-1)→θ(n).And this procedure repeats for the next lower order situation, that is,and we get ¨w→¨wd.Thus the equilibrium point for the tracking task of the end effector is
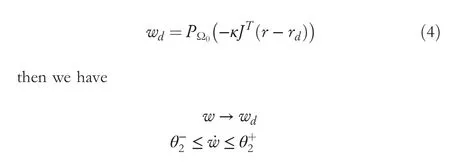

and we get ˙w= ˙wdfinally by the recursive updating of the corresponding recurrent neural network solver.
3 | CASCADED RECURSIVE RECURRENT NEURAL NETWORK
In order to achieve kinematic control of the manipulator with all levels of joint constraints, based on the aforementioned discussions,we have the equilibrium points in a different order as follows:
wherePΩ1(?),PΩ2(?),PΩ3(?), …,PΩi(?), …,PΩn-1(?),PΩn(?)denote the piecewise linear projection function arrays for the solution sets Ω1, Ω2, Ω3, …, Ωi, …, Ωn-1, Ωnin different levels of time derivatives for joint variables, andk1,k2,k3, …,ki, …,kn-1,kndenote the convergence scaling parameters for desired equilibrium points in different levels of time derivatives for joint variables, which are all positive scalars.
In order to track the aforementioned equilibrium points in different levels, we first define the following state variables for constructing a state-space dynamic model which can describe the time derivatives of different orders for the state variables of the recurrent neural network solver
The state-space dynamic model is constructed as follows:
Therefore, the equilibrium points can be described by the state variables as follows:
Next, we define the congregation state variable vector as the following form
Thus,we can get the following state-space dynamic equations
wheref(?)denotes the mapping function arraywhich is composed of the linear projection function arraysPΩ1(?),PΩ2(),…,PΩn-1(?).The first equation is a fast-manifold relative to the second equation whenkn?1.Applying a singular perturbation analysis[28],we conclude the following slow manifold ˙xn-2with the faster manifold ˙xn-1as follows:where 0 <1/kn≤1.We expect the manifold system, which is also a recursive recurrent neural network solver, can converge to the equilibrium points when dealing with the kinematic control of the manipulator system with high-level joint constraints involved as shown in Figure 1.In the recurrent neural networks with different solution sets, the higher order desired target variables are gradually generated as the inputs until the highest desired one is satisfied, and then the resolved joint angular variables in descending orders are generated until the resolved joint velocity variable is obtained.In this manner,lower order desired end-effector variable is acting as the input to the recurrent neural network model with a corresponding solution set to generate the output as the higher order desired end-effector variable, and higher order desired joint angular variable is acting as the input to the recurrent neural network model with the corresponding solution set to generate the output as the lower order joint angular variable.The overall computational complexity depends on the calling times of the primal-dual neural networks,but the dimension of the network variables is not increased which does not increase the complexity of each single constrained optimization.In the ensuing sections,we present the stability analysis and show the convergence properties.
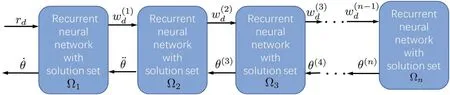
F I G U R E 1 Flow chart of the proposed recursive recurrent neural network model for kinematic control with different level of physical constraints satisfied
4 | THEORETICAL ANALYSIS
In this section,we present a theoretical analysis on the solution of the control actions by the aforementioned recursive neural network based on the manifold system with stability and convergence results provided.
4.1 | Constraint compliance analysis
For the manifold system equations
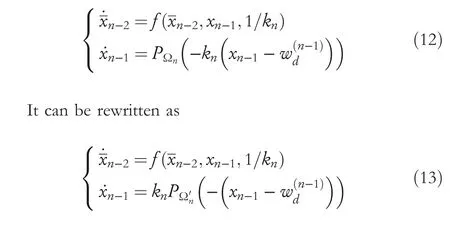
where solution set cone Ω′nis scaled by the parameterknfrom the original solution set cone Ωn.
Therefore, the equations above can be equivalently

4.2 | Stability and convergence analysis of intermediate variables for high‐order joint constraints
Review the second equation of the manifold system
According to the definition of the piecewise linear projection functionPΩn(?), we have



Generally,based on the aforementioned derivations,we can summarise that for the manifold system equation
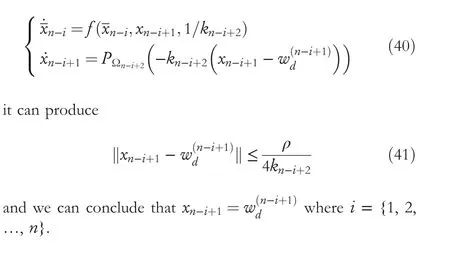
4.3 | Stability and convergence analysis for the end effector in tracking path
After showing the stability and convergence of the state-space dynamic systems with intermediate variables for high-order constraints, we still need to analyse the stability and convergence properties for the end effector of the manipulator system to track the desired path.According to the velocity kinematics equation and the proposed recursive recurrent neural network solver, we define the terme=r-rdas the tracking error of the end effector of the manipulator, and we have

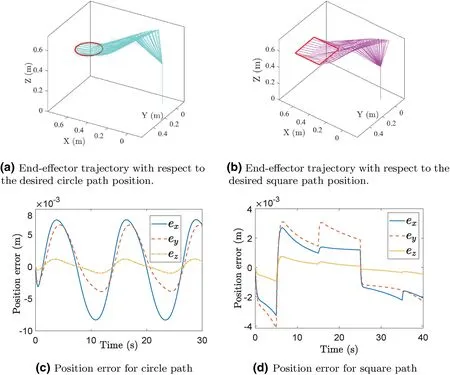
F I G U R E 2 Tracking performance of circle and square paths by the proposed method.

we can get
The equation above can be equivalent to
Therefore, we have the following inequality
That is
There exists a valueρ> 0 such that
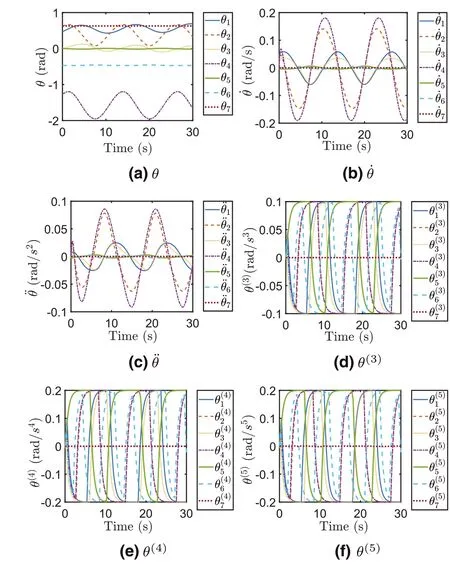
F I G U R E 3 Joint variables of different orders in motion planning of the manipulator for circle path tracking by the proposed method.

If the Jacobian matrix is full rank, which means the manipulator will not fall into the singularity situation during motion control process, then we have
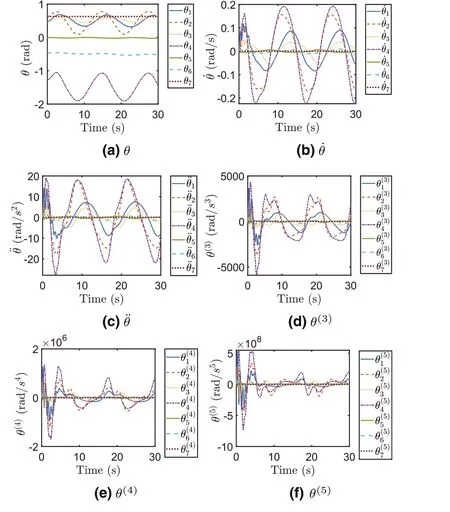
F I G U R E 4 Joint variables of different orders in motion planning of the manipulator for circle path tracking by the pseudoinverse method.
which indicates that the tracking error of the end effector of the manipulator can converge to zero.
5 | RESULTS

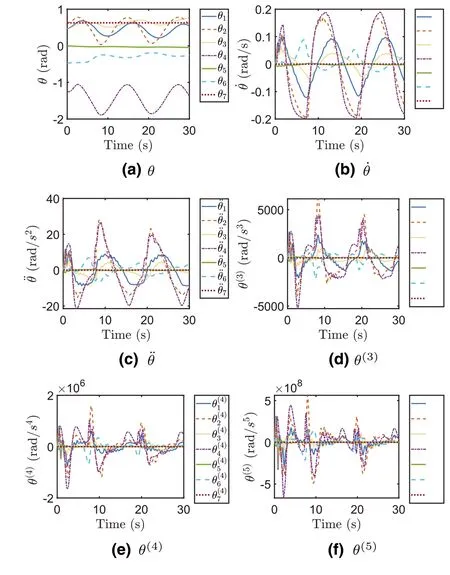
F I G U R E 5 Joint variables of different orders in motion planning of the manipulator for circle path tracking by the conventional recurrent neuralnetwork method.
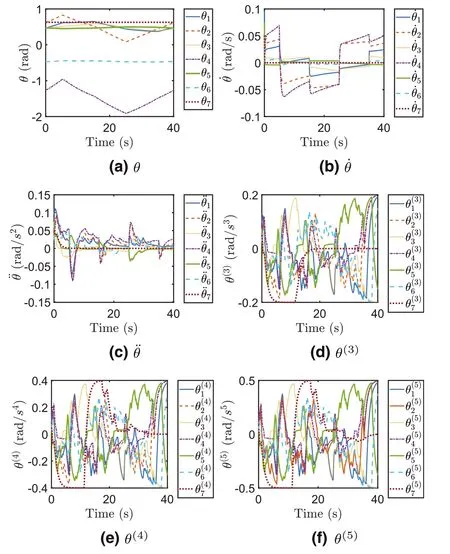
F I G U R E 6 Joint variables of different orders in motion planning of the manipulator for square path tracking by the proposed method.
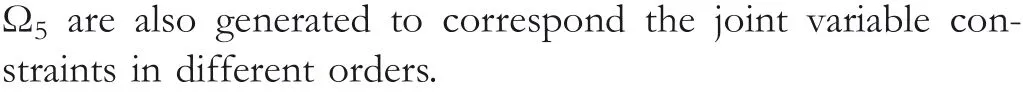
5.1 | Simulation setup and parameter configuration
In the simulation, we evaluate the performance for the Kuka manipulator by the proposed method.The forward kinematics modelling of the manipulator is established based on the D-H table in ref.[2].


5.2 | Tracking performance
F I G U R E 7 Joint variables of different orders in motion planning of the manipulator for square path tracking by the pseudoinverse method.
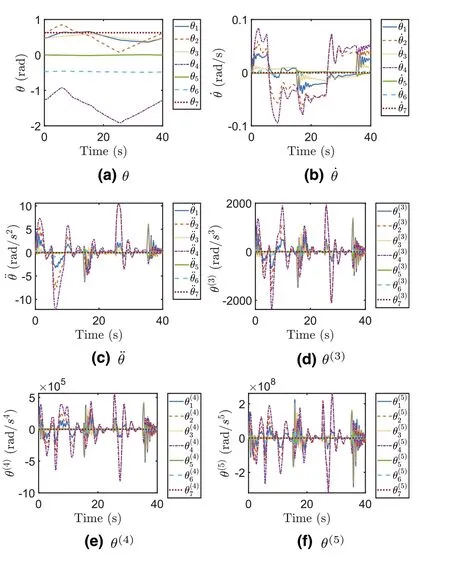
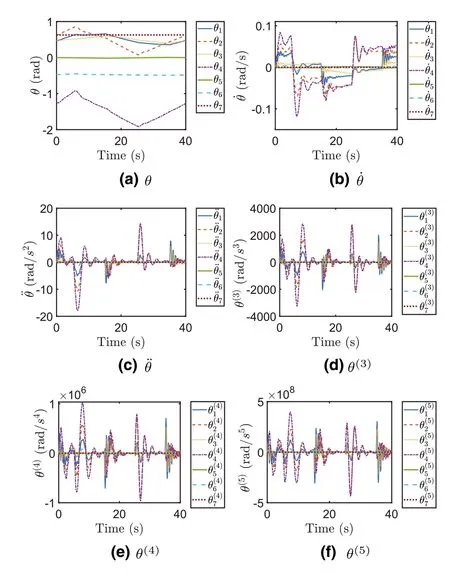
F I G U R E 8 Joint variables of different orders in motion planning of the manipulator for square path tracking by the conventional recurrent neural network method.
Figure 2 shows the tracking performance of the manipulator for circle and square paths by the recursive recurrent neural network solver (62) with the aforementioned parameters configured.From Figure 2a and 2b,we could observe that,the manipulator can fulfil the path tracking tasks well with its end effector promisingly following the positions of the paths.As seen from Figure 2c and 2d, the position errorse=[ex,ey,ez]between the end effector and the desired paths can be rather small,with the range being from less than 10×10-3m for the circle path and less than 8×10-3m for the square path.These results demonstrate the efficiency of the proposed recurrent neural network solver based on the manifold system for kinematic control of the manipulator in the aspect of tracking accuracy.
5.3 | Joint constraints
In additional to fulfiling path tracking control,the manipulator system has to simultaneously follow the joint constraints in different orders.Figures 3 and 6 show the joint variables of different orders for circle and square path tracking tasks by the proposed method, that is, joint angles, joint angular velocity,joint angular acceleration, joint variable of third order, joint variable of fourth order, and joint variable of fifth order.
For the circle path tracking task, Figure 3a shows the revolved joint angle,and Figure 3b-f show other joint variables of different orders which have to be within the aforementioned constraints.Clearly seen from Figure 3, the joint angular velocity ˙θsuccessfully falls into[-0.2 0.2]rad/s,the joint angular acceleration ¨θfalls into [-0.1 0.1] rad/s2, the joint variable of the third orderθ(3)falls into[-0.1 0.1]rad/s3,the joint variable of the fourth orderθ(4)falls into[-0.2 0.2]rad/s4,and the joint variable of the fifth orderθ(5)falls into [-0.2 0.2] rad/s5.Together with the tracking results of the end effector in Section V-B for circle path tracking, the proposed method is demonstrated as an efficient way to deal with joint constraints in high order when fulfiling kinematic control.For comparisons, Figures 4 and 5 show the joint variables of different orders based on the pseudoinverse method and the conventional recurrent neural network method in the circle path tracking tasks, and it can be observed that, when encountering the higher order (>= 2) joint constraints (shown in Figures 4c-f and 5c-f, these two methods cannot work well as the higher order joint variables obviously exceed the corresponding joint limits.
For the square path tracking task, Figure 6a shows the revolved joint angle,and Figure 6b-f show other joint variables of different orders which have to be within the aforementioned constraints.Clearly seen from Figure 6, the joint angular velocity ˙θsuccessfully falls into [- 0.1 0.1] rad/s, the joint angular acceleration ¨θfalls into [- 0.15 0.15] rad/s2, the joint variable of the third orderθ(3)falls into[-0.2 0.2]rad/s3,the joint variable of the fourth orderθ(4)falls into[-0.4 0.4]rad/s4,and the joint variable of the fifth orderθ(5)falls into[-0.5 0.5] rad/s5.Together with the tracking results of the end effector in Section V-B for square path tracking, the proposed method is demonstrated as an efficient way to deal with the joint constraints in high order when fulfiling kinematic control.Furthermore, Figures 7 and 8 show the joint variables of different orders based on the pseudoinverse method and the conventional recurrent neural network method in the square path tracking tasks, respectively and it can be observed that,when encountering the higher order (>= 2) joint constraints(shown in Figure 7c-f and Figure 8c-f), these two methods cannot work well as the higher order joint variables evidently exceed the corresponding joint limits.
To summarise,from all these results including comparisons,we can conclude that the proposed recursive neural network method is efficient and superior for the manipulator control with high-order joint constraints.
6 | CONCLUSION
Due to physical limitations and actuation saturation of manipulator joints, the involvement of joint constraints for kinematic control of manipulators is essential and critical.In this work,for the first time,a novel recursive recurrent network model is proposed to solve the kinematic control issue for manipulators with different levels of physical constraints, and the proposed recursive recurrent neural network model can be formulated as a new manifold system to ensure a control solution within all of the joint constraints in different orders.Theoretical analysis shows the stability and convergence of the purposed recursive recurrent neural network and its convergence of solution.Simulation results further demonstrate the effectiveness and superiority of the proposed method in endeffector path tracking control under different levels of joint constraints based on the Kuka manipulator system.
ACKNOWLEDGMENT
This work is partially supported by the IMPACT Fund of Swansea University.
CONFLICT OF INTEREST
The authors declare that there is no conflict of interest.
DATA AVAILABILITY STATEMENT
The running data/code that support the findings of this study are available from the corresponding author upon reasonable request.
ORCID
Zhan Lihttps://orcid.org/0000-0002-3928-1642
 CAAI Transactions on Intelligence Technology2023年3期
CAAI Transactions on Intelligence Technology2023年3期
- CAAI Transactions on Intelligence Technology的其它文章
- Fault diagnosis of rolling bearings with noise signal based on modified kernel principal component analysis and DC-ResNet
- Leveraging hierarchical semantic‐emotional memory in emotional conversation generation
- Forecasting patient demand at urgent care clinics using explainable machine learning
- A federated learning scheme meets dynamic differential privacy
- SRAFE: Siamese Regression Aesthetic Fusion Evaluation for Chinese Calligraphic Copy
- Wafer map defect patterns classification based on a lightweight network and data augmentation
