Lie Liu(劉列), Ying Han(韓穎), Jiayu Huo(霍佳雨),?,Honglin Wen(文紅琳), Ge Wu(吳戈), and Bo Gao(高博)

1College of Communication Engineering,Jilin University,Changchun 130012,China 2College of Electronic Science and Engineering,Jilin University,Changchun 130012,China

Keywords: pure-quartic soliton,pulsating soliton,erupting soliton,passively mode-locked fiber lasers

1.Introduction

High-energy soliton fiber lasers have been a research hotspot due to their wide range of applications.[1–7]For solitons which are produced by the balance between second-order dispersion (β2) and the self-phase modulation (SPM) effect,energy is proportional to the first power of the inverse pulse duration (τ):E=2|β2|/(γτ),[8]which limits the increase in energy.Third-order dispersion (β3) will cause solitons to be unstable; however, the existence of negative fourth-order dispersion (β4) will make solitons stable.In 1994, researchers found quartic soliton solutions with oscillating tails and a flatspectrum center of nonlinear Schr¨odinger equations(NLSEs),which consider both negativeβ2andβ4,[9–12]Quartic solitons originate from the balance between the negativeβ2and the SPM effect but are modified byβ4.After more than 20 years of stagnation in the research of quartic solitons, in 2016, Blanco Redondoet al.found pure-quartic solitons(PQSs) that originate from the balance between the negativeβ4and SPM effect in photonic crystal waveguides.[13,14]The energy of PQSs is proportional to the third power of inverseτ:EPQS= 2.87|β4|/(γτ3),[15]which means the narrowerτleads to higher energy.The conditions required to obtain PQSs require platforms to have a large negativeβ4, wide bandwidth, and sufficient nonlinearity.In addition,β3at the central wavelength must be close to zero.[16]Photonic crystal waveguides,[13,14,16]silicon-based waveguides,[17]and optical Kerr microcavities[18–20]can meet the above conditions to achieve PQS output.

The research on PQSs in fiber and fiber lasers began in 2018; Blanco Redondoet al.designed the microstructured fiber supporting the generation of PQSs, laying a foundation for PQS fiber lasers.[21]Subsequently,they proved that the coexistence ofβ2andβ4can improve the performance of NLSEbased fiber lasers.[22,23]The above numerical results provide theoretical support to the building of PQS fiber lasers.[24–26]Later, they achieved PQS output from dispersion-managed fiber lasers[27,28]and numerically analyzed their oscillation characteristics.[29]Luoet al.employed the same theoretical model to investigate pulsating PQSs.[30]Other researchers have used NLSE-based fiber lasers dominated byβ4to theoretically study vector quartic-solitons.[31]Research on the performance and dynamic characteristics of PQS fiber lasers needs to be carried out.

In this work,we numerically investigate the pulsating and erupting dynamics in PQS fiber lasers.We study the effects of the saturation power,small-signal gain,and output coupler on PQS dynamics under different gain bandwidths(?g).The results show that PQSs experience several stages,including stationary PQSs, pulsating PQSs, and creeping PQS molecules with modulated parameters under?g= 50 nm conditions.Meanwhile,when we consider the influence of high-order dispersion and the spectral filtering effect on eruption characteristics,PQSs experience stationary PQSs,pulsating PQSs,erupting PQSs, periodically erupting PQSs, and PQS molecules with modulated parameters when?gis 10 nm.PQSs exhibit similar dynamic characteristics under three modulated parameters,in which the small-signal gain corresponds to the pump power in experiments and is a more extensive research object.This paper therefore uses the influence of small-signal gain as an example to analyze PQS dynamic characteristics.These results will provide a physical mechanism for PQS dynamics.

2.Numerical method

Figure 1(a) presents the scheme of a PQS fiber laser,which contains a pump source, a wavelength division multiplexer, Er-doped fiber, a fiber polarizer, a polarization controller, an isolator, a saturable absorber (SA), a pulse shaper,single-mode fiber,and an output coupler(OC).Pulse transmission in the fiber is simulated by NLSE

whereAis the pulse slowly varying complex envelope.Here,γ,β2,β3, andβ4represent the nonlinear coefficient, and the second-order, third-order, and fourth-order dispersion coefficient of the fiber, respectively, andTis the time coordinate.Meanwhile,gis the gain of the Er-doped fiber,written as

whereg0,?g, andEsatrepresent the small-signal gain, gain bandwidth,and saturation energy,respectively.Here,

is the pulse energy,whereTRis the roundtrip(RT)time.The SA is modeled by

whereq0,Psat,and|A(z,T)|2are the modulation depth,saturation power,and instantaneous pulse power,respectively.

The fixed parameter values in this simulation are given in Table 1, and the other parameters are variables.The pulse shaper,which can compensate for intra-cavityβ2andβ3while providing a large negativeβ4, is modeled by multiplying the electric field by the phase in the frequency domain in simulation.[15]This meansβ2,β3,andβ4of the pulse shaper in Table 1 can fully compensate for intra-cavityβ2,β3to nearly zero and provide sufficientβ4to obtain PQSs.The time resolution is 50 fs and the center wavelength is set near 1550 nm.

Table 1.Parameter values used in the simulation.

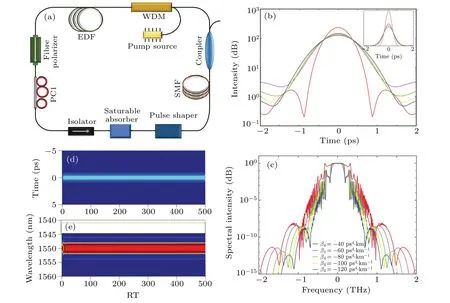
Fig.1.(a)A scheme of the PQS fiber laser.(b)Logarithmic scale time profiles(inset: time profiles)and(c)the spectrum of stationary PQSs obtained with different β4.Evolution of(d)the time profiles and(e)spectrums when β4 of the pulse shaper is set to-80.0022 ps4/km(inset in(e): energy).

TheEsat,Psat,g0, and output ratio of the OC (Rout) are set as 300 pJ,200 W,3.45 m-1,and 50%,respectively,to obtain stationary PQSs.The PQS logarithmic scale time profiles shown in Fig.1(b) present oscillating tails.Figure 1(c)exhibits that the change in the spectrum intensity is less pronounced but becomes flatter.Figures 1(d) and 1(e) present the time profile evolution and spectrum evolution of PQSs to demonstrate their stability.Typically, traditional solitons exhibit pulsating dynamics or erupting dynamics with modulated system parameters;[32–36]it is therefore interesting to examine whether PQSs have similar dynamics with altered system parameters.Therefore, we comprehensively study the effects ofPsat,g0, andRouton PQS dynamics.It was found that there are pulsating single PQSs to creeping PQS molecules with the changes inPsat,g, orRoutunder different gain bandwidths (50 nm, 40 nm, 30 nm, 20 nm).However, pulsating PQSs, erupting PQSs, periodically erupting PQSs, and PQS molecules appear when?g=10 nm.The above results are analyzed in detail below.It should be noted that the PQS dynamics with modulatedPsat,g0,andRoutare qualitatively consistent when?g=50 nm,40 nm,30 nm,and 20 nm;we have therefore taken?g=50 nm and 10 nm as the examples in this paper.Meanwhile,due to the importance of small-signal gain,it is taken as an example for analysis in this paper.

3.Influence of system parameters on purequartic soliton dynamics

3.1.Influence of small-signal gain under 50 nm

Modulated pump power in experiments corresponds to a changegin simulation, which will cause different soliton dynamics.In the simulation of this section,?g,Esat,Psat, andRoutare 50 nm, 300 pJ, 200 W, and 50%, respectively.The influence ofgon soliton characteristics is investigated by linearly increasinggfrom 0.1 m-1with a step of 0.1 m-1.The fiber laser outputs stationary PQSs whengis less than 28.1 m-1, but splitting occurs whengis increased to～1 m-1without the intra-cavity pulse shaper.[25]PQSs can endure large nonlinear phase shifts without splitting and have large pulse energy.[29]Pulsating PQSs appear whengis in the range of 84.2 m-1–136.9 m-1.Figure 2 reveals the time profile evolution, spectrum evolution, energy variation, and single-shot spectrum of pulsating PQSs whengis 90 m-1.Figures 2(a)and 2(b)show that the time profile evolution of PQSs exhibits oscillation,while the spectrum evolution exhibits breathing, and its energy also changes periodically.Intensity exchange between sidebands and the center of the soliton spectrums makes breathing appear during PQS spectrum evolution,which is also the cause of pulsating traditional solitons:[25]specifically, pulsating PQSs occur.Figure 2(c)reveals the spectrum evolution of 10 RTs,and Figs.2(d)–2(g)show single-shot spectrums during one pulsating period to further analyze the causes of the pulsation.The pulsating period is about 5 RTs in Fig.2(c),which means that the intensity exchange of the spectrum center with sidebands is within 5 RTs and is restored to the original state after 5 RTs.Single-shot spectrums of PQSs have high-intensity Kelly sidebands, similar to traditional solitons, while PQS spectrums have multilow-intensity sidebands under the influence ofβ4.[13,15]This makes it easier to produce energy exchange between sidebands and the spectrum center, which makes it easier to obtain pulsating PQSs.Specifically,the intra-cavity largeβ4is the cause of pulsating PQSs.

Fig.2.Evolution of(a)the time profiles and(b)spectrums when g0=90 m-1 (inset in(b): energy).(c)The extracted spectrum evolution of(b).(d)–(g)Single-shot spectrums at different RTs in one pulsating period.

The PQSs split into PQS molecules wheng0is further increased to 137 m-1, creeping PQS molecules occur wheng0= 370.5 m-1, and the output of the fiber laser becomes chaotic wheng0reaches 475.7 m-1.When we compare Fig.3 with the results in Refs.[37–39], it can be proved that the double solitons we observed also exhibit similar snaking behavior in the time domain,which is generally called creeping solitons and belongs to a type of pulsating solitons.Specifically,PQS molecules creeping in the time domain(Figs.3(a)–3(f))and breathing during spectrum evolution(Figs.3(g)–3(l))are induced by periodic attraction and repulsion between two PQSs, which also induces the periodic variation of the pulse energy.The creeping distance(period)of the PQS molecules first decreases then increases, and the interval between them also shows the same trend with the continuous increase ing0.The interval between two creeping PQSs attains the maximum wheng0reaches a certain level, but its creeping distance is minimum (Fig.3(f)), which may be due to the fact that the large pulse energy of the PQSs makes the energy exchange and interaction between two PQSs easier at this time.It is also easier to reach different equilibrium states(creeping).The larger creeping distance makes spectrum breathing more obvious, i.e., it exhibits more obvious pulsation behavior.Theβ4leads to PQS spectrums with multi-sidebands,[13,15]making it easier to produce energy exchange between the sidebands and the spectrum center.Specifically, the appearance of creeping PQS molecules is related to the intra-cavity largeβ4.

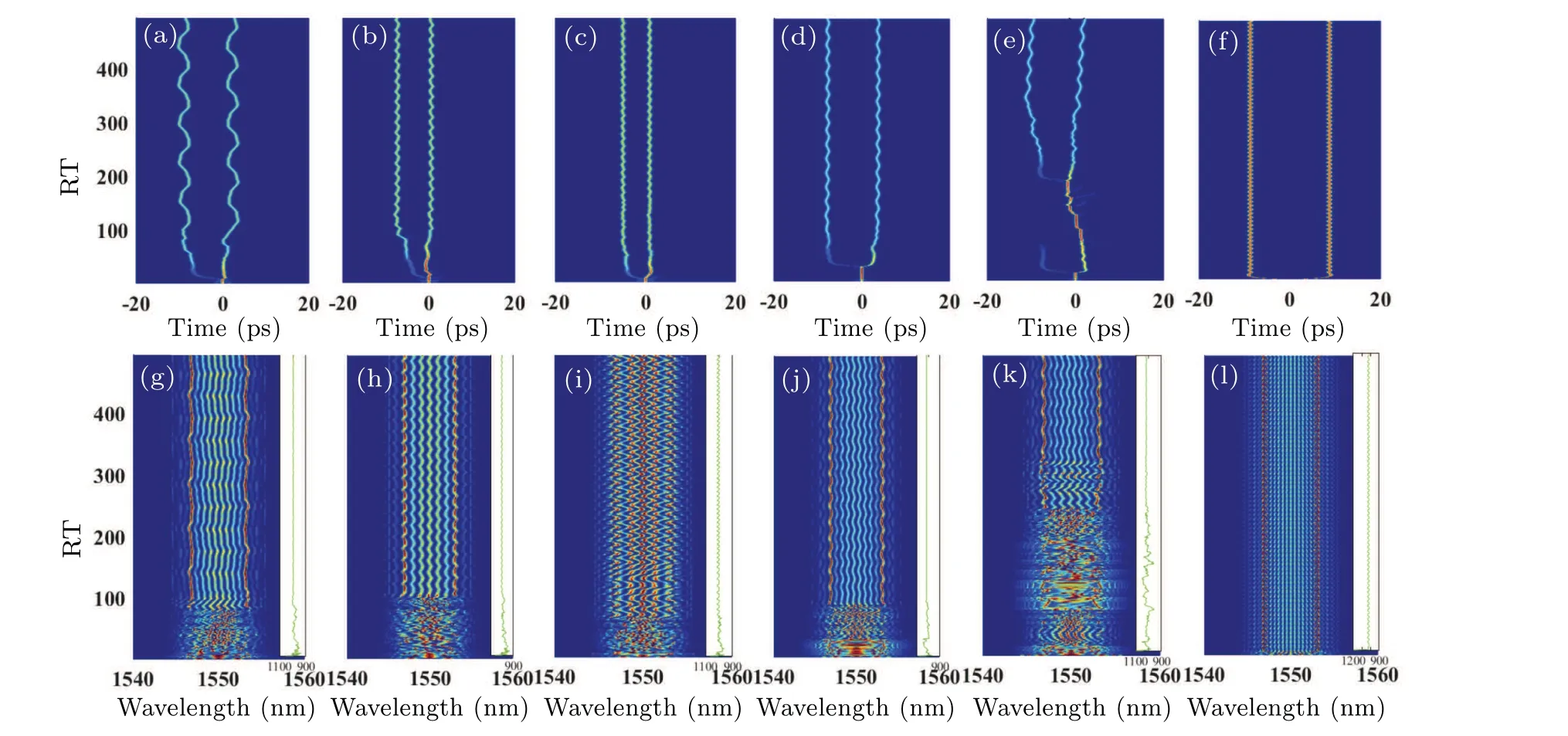
Fig.3.Evolution of (a)–(f) time profiles and (g)–(l) spectrums when g0 =370.5 m-1, 380.8 m-1, 394.6 m-1, 431.1 m-1, 444.7 m-1, and 475.7 m-1 (inset in(g)–(l): energy).

3.2.Influence of small-signal gain under 10 nm

Limited by the size of the fiber core, soliton transmission is affected by many factors in passively mode-locked fiber lasers; these are not only the pumping capacity but also the nonlinear effect, group velocity dispersion effect, and?gcaused by doped ions.The gain spectrum is related to the doping concentration,fiber length,and pump power in actual production.It is necessary to explore the effect of?gon soliton dynamics.The influence ofPsat,g,andRouton PQS dynamics(?g= 10 nm) is investigated.It is found that the parameter value required for splitting is low, which may be related to the narrow?g.Fiber lasers have a significant impact on amplification when the spectrum width of the soliton is close to?g.Solitons with a narrower pulse width(wider spectrum width)have higher energy according to the energy-width scaling law of PQSs:namely,?g=10 nm limits the amplification ability of fiber lasers in this simulation.At the same time,the change in spectrums upon amplification makes it act as a spectral filter, resulting in erupting PQSs, similar to the results in Ref.[40].PQSs, pulsating PQSs, erupting PQSs, and PQS molecules appear successively as altered system parameters.

The?g,Esat,Psat, andRoutare 10 nm, 120 pJ, 50 W,and 50%, respectively, in this section.Thegis linearly increased from 0.1 m-1in a step of 0.1 m-1to study the effect of pump power on PQS dynamics.The fiber laser outputs stationary PQSs whengis less than 3.5 m-1;pulsating PQSs and the phenomenon similar to that presented in Subsection 3.1 appear with the continuous increase ing.Figures 4(a)–4(d)display the time profile evolution,spectrum evolution,and energy change of the process from pulsating PQSs to erupting PQSs and then to PQS molecules.It can also be seen as the build-up of PQS molecules,which is different from the experimental results observed in mode-locked lasers with onlyβ2.The build-up of dissipative soliton molecules always involves complex interactions among solitons,[29,41]while the build-up of traditional solitons has a big corner.[42]The field autocorrelation trace of PQS molecules in Figs.4(i)and 4(j)shows that there is no complex interaction before the formation of stable PQS molecules, but eruption exists, which may be related to the intra-cavity large negativeβ4.

Figures 4(e)–4(h) present the single-shot spectrums, and the single-shot time profiles of pulsating PQSs are presented in Figs.4(a)–4(d).The time-domain oscillating tail and breathing spectrum at?g=10 nm are more obvious compared with pulsation at?g=50 nm.Due to the fact that they are characterized by successive or periodic time shifts,spectrum fragmentation, and energy improvement, some researchers classify erupting traditional solitons as pulsating,[34–36,41,43–46]but more researchers classify this as explosion.[47–51]Also, the time profile evolution of erupting PQSs in Figs.5(a)and 5(b)reveals the quartic time shifts of PQSs, i.e., one typical eruption characteristic.It can be seen that although the pulsating characteristics of the PQSs are similar under two values,their eruption processes are significantly different.Also, the second PQSs appear at different time delay positions, i.e., the erupting direction of the PQSs is not fixed, but it will cause an increase in pulse intensity and energy, laying a foundation for subsequent splitting.The nonlinear phase shift that is accumulated(related to intensity)after the solitons run one RT will affect the shape of the soliton spectrums or time profiles,and even cause solitons to split.[52]The single-shot time profiles of the erupting PQSs in Figs.5(a) and 5(b) indicate that during successive eruption,the intensity may be continuously increased(Fig.5(a)),or there may be a tiny weakening(Fig.5(b)), resulting in the accumulation of different nonlinear phase shifts,so that the second PQS after splitting appears at different time delay positions.The fragmented single-shot spectrum in Figs.5(c)and 5(d)further proves the existence of erupting PQSs after pulsating and different erupting intensities caused different degrees of fragmentation.High-order dispersion and high-order nonlinearity have important influences on erupting traditional solitons,[48]and proper pairwise conjugation of these high-order effects can eliminate eruption.[47,49]Therefore,erupting PQSs can be attributed to the intra-cavity large negativeβ4in this simulation.

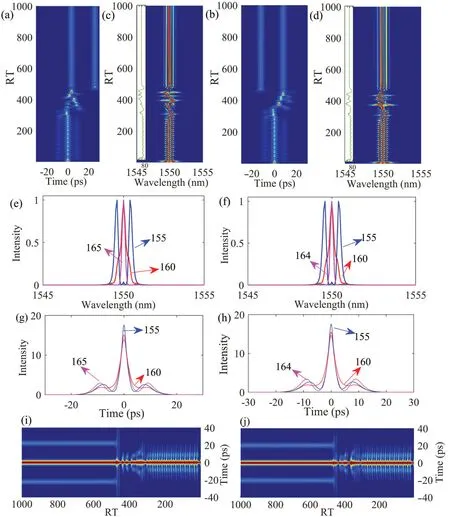
Fig.4.Evolution of(a),(b)the time profiles,(c),(d)spectrums,and(i),(j)field autocorrelations when g=9.1 m-1,9.2 m-1 (inset in(c),(d):energy).Single-shot(e),(f)spectrums and(g),(h)time profiles at different RTs in one pulsating period.

For erupting traditional solitons,periodic eruption will appear when one adds high-order nonlinearity and high-order dispersion to equations to model soliton transmission.[47–49]The time profile evolution will show periodic time shifts.An intra-cavity large negativeβ4makes the PQSs exhibit similar periodic eruption in this simulation.An example is shown in Figs.6(a)–6(c),where PQSs first pulsate and then erupt periodically.The 3D time profile evolution of erupting PQSs shown in Fig.6(d)shows that PQSs erupt periodically with two peaks as one period,making the spectrum evolution exhibit periodic changes(Fig.6(e)).Single-shot spectrums of the erupting PQSs will also be“broken”(Figs.6(f)–6(i)),but they will return to the original spectrum shape at the beginning of a new eruption period(Fig.6(j)).The center of the time profiles moves slightly and the intensity of the oscillating tails changes slightly during eruption(Fig.6(k)),which is also important for periodically erupting PQSs.

4.Conclusion

In conclusion, we numerically found that the gain bandwidth, saturation power, small-signal gain, and splitting ratio of the output coupler in passively mode-locked fiber lasers will all affect PQS dynamics.Stationary PQSs, pulsating PQSs,and creeping PQS molecules appear one after another with modulated parameters when?g= 50 nm.The analysis of single-shot spectrums and single-shot time profiles in one pulsating period proved that pulsating PQSs can be attributed not only to its oscillating tail but also to an intra-cavity large negativeβ4.The?gis also a limiting factor for soliton transmission in passively mode-locked fiber lasers.PQSs appear as pulsating,erupting,periodically erupting,and splitting in turn with modulated parameters when?g=10 nm,which is quite different from the pulsating dynamics at 50 nm.This may be due to the change in the soliton spectrum caused by the narrow gain bandwidth during amplification, which makes it act as a spectral filter.At the same time, the influence of highorder dispersion and high-order nonlinearity on erupting traditional solitons,erupting PQSs,and periodically erupting PQSs in this simulation can also be attributed to the intra-cavity largeβ4.These results deepen our understanding of PQS dynamics,such as high-energy erupting PQSs.

Acknowledgement

We acknowledge the financial support from Science and Technology Project of the Jilin Provincial Department of Education(Grant No.JJKH20231171KJ).