Zhenpeng Wang(王振鵬), Maomao Gong(宮毛毛),,?, Xingyu Li(李星宇),Songbin Zhang(張松斌), and Xiangjun Chen(陳向軍),2,?

1Hefei National Research Center for Physical Sciences at Microscale and Department of Modern Physics,University of Science and Technology of China,Hefei 230026,China

2Hefei National Laboratory,University of Science and Technology of China,Hefei 230088,China

3School of Physics and Information Technology,Shaanxi Normal University,Xi’an 710119,China

Keywords: (e,2e),multi-center distorted-wave method(MCDW),vibrational effect

1.Introduction

The electron-impact ionization is a fundamental process in atomic and molecular physics.[1]It plays an essential role in plasma physics, astrophysics, as well as in biological radiation physics.The accurate and reliable data of the ionization cross sections are of great importance both experimentally and theoretically.The complete information of the ionization dynamics can be obtained by the kinematically complete (e,2e)experiment, where the energies and momenta of the incoming and two outgoing electrons are determined.The quantity measured in such experiment is the so-called triple-differential cross sections (TDCSs).The experiments were usually performed at low(<100 eV)[2,3]or medium(～250 eV)[4–7]incident energy employing traditional(e,2e)setup[8]or reaction microscope,[9]to test theoretical models concerning few-body dynamics in quantum mechanics.

For simple atoms and molecules,[10–13]the measured TDCSs can be reproduced by the nonperturbative theories such as the exterior complex scaling(ECS),[14]the converged close-coupling (CCC),[15]the time-dependent close-coupling(TDCC),[16]as well as the B-splineR-matrix[17]approaches.For more complex molecules, on the other hand, due to the multi-center character and the complex electronic structures,it is still challenging to precisely describe the electron-impact ionization cross sections.Perturbative methods are more practical.Madisonet al.developed a molecular three-body distorted wave(M3DW)method[18–24]to calculate the TDCSs of molecules.In their approach, the continuum wave functions of the incident, scattered and ejected electrons are solved in a spherically averaged distorting potential.Due to the large computational quantities, the orientation-averaged molecular orbital(OAMO)approximation is usually adopted,which neglects the anisotropic property of the molecule.A proper average(PA)over orientation-dependent cross sections is also employed by the same authors[25–31]and the agreement between theory and experiment is generally improved.A multi-center distorted-wave (MCDW) method was reported by Zhanget al.[32]to describe the single-ionization dynamics for asymmetric kinematic conditions, and has been employed to calculate TDCSs for a series of molecules.[32–37]In the MCDW method, the incident and scattered electrons are described by plane waves, and the continuum wavefunction of the ejected electron is solved under the multi-center molecular ion potential.This method was recently extended to more general situations by including the distorted waves of the projectiles,[38,39]called multi-center three-distorted-wave (MCTDW) method.Mouawadet al.[40–43]investigated the TDCSs for molecules in the coplanar asymmetric geometry using a Coulomb wave and a simplified distorted wave methods within the first Born approximation.

Despite the great efforts of the theorists, discrepancies between experiments and theoretical calculations still remain.It is worth to note that, in all the theoretical methods concerning (e,2e) dynamics for molecular targets, the TDCSs were calculated at the equilibrium molecular geometry.However, according to some recent studies on electron momentum spectroscopy(EMS),[44–49]whose theoretical framework is the simple plane wave impulse approximation,molecular vibrational motions may have significant effect on the electron momentum distributions for molecular orbitals.Such effect has also been demonstrated in the temperature dependence of electronic transition probabilities,[50,51]electric dipole moment[52–54]and generalized oscillator strengths(GOSs)[55–60]of molecules.Therefore, it is highly necessary to develop a theoretical approach including vibrational motions for calculating(e,2e)TDCSs of molecules.

In the present work, the multi-center distorted-wave method[33]has been modified by including molecular vibrations.This vibrational multi-center distorted-wave method(v-MCDW) is then employed to calculate the (e,2e) TDCSs for the 1b3gorbital of ethylene molecule.Typical kinematic arrangements in coplanar asymmetric geometry are chosen: 1)incident electron energyEi=250 eV with ejected electron energiesEe=8 eV,12 eV,20 eV,37 eV,74 eV and scattering anglesθs=-6?,-10?;2)incident electron energyEi=100 eV with ejected electron energiesEe=5 eV, 10 eV, 15 eV and scattering anglesθs=-6?,-10?.A harmonic analytical quantum mechanical approach(HAQM)[44]is employed to include the vibrational motions of ethylene molecule in the calculations.The TDCSs calculated at equilibrium molecular geometry and including molecular vibrations are compared.The results show that the vibrational motions significantly influence the angular distributions of the TDCSs,especially in the binary region along momentum transfer near the Bethe ridge.

This paper is organized as follows: The theory of the v-MCDW[33]method is presented in Section 2.The calculated TDCSs including molecular vibrations and a comparison with the results calculated at equilibrium geometry are given in Section 3, followed by a summary in Section 4.Atomic units(a.u.) are used throughout the paper unless explicitly stated.

2.Theoretical method

2.1.Scattering theory of molecule under the Born–Oppenheimer approximation

According to the scattering theory, the electron impact single ionization process can be described by a transition matrixTfibetween the initial and final states of the scattering system through the interaction potential.Within the Born–Oppenheimer approximation and assuming that the rotational–vibrational coupling is small, the wave functions for the molecular target and ion can be written as a product of rotational,vibrational and electronic wave functions.Using the sum rule for the initial rotational states and closure relation for the final rotational states, the scattering amplitude can be written as

whereΦiandΦfare the initial and final electronic wavefunctions of the scattering system, respectively, depending on the nuclear coordinatesQ.??is the rotation operator in the laboratory framework.?=(α,β,γ) is the Euler angle which defines the molecular orientation.χivandχfv′are the vibrational wave functions of the initial and final states.Summing over the final vibrational states,the magnitude squared of the transition matrixTfiis

2.2.Multi-center distorted wave method

In the present coplanar asymmetric kinematic arrangements, the incident and scattered electrons are moving fast,and can be approximately described by the plane waves.In the MCDW method,the electronic scattering amplitudetfi(?)can be expressed as[33]

whereriandrjare the position vectors for the incoming electron and thejth bound electron of the target,respectively.Under the sudden approximation,tfican be simplified as

where the Bethe integral technique is used.K=ki-ksdenotes the momentum transfer.φαis the wave function of the ionized bound orbital.?(-)is the continuum wave function of the ejected electron,which is solved under the multi-center molecular ion potential:

whereVm=Vst+Vcpis the model potential.[61]VstandVcpare the static and correlation-polarization potentials, respectively.The single-center expansion is used to solve the equation, in which the wave function and potential are expanded by the symmetry-adapted angular functions.[61–63]Substituting Eq.(10)into Eq.(5),σeis then obtained by averaging over all possible molecular orientations.

2.3.Harmonic analytical quantum mechanical approach

In order to take into account the molecular vibrations,HAQM approach[44]is adopted.In this approach, the vibrational wave functionχivis approximated by the product of the harmonic oscillator functionsξvL.Then Eq.(6)can be written as

In the practical calculation,we assume that the vibrational contributions of each vibrational mode can be approximately written as quadratic polynomials of the normal coordinates.Assuming a Boltzmann distribution for the initial vibrational states,the vibrationally averaged TDCS can finally be written as

wherePnL(T)represents the probability in the vibrational levelvand vibrational modeLat temperatureT,nLandωLare the vibrational quantum number and angular frequency of theLth normal mode, respectively.cL,2andcL,4represent the quadratic polynomials fitting coefficients.In order to obtaincL,2andcL,4,a set ofσeare calculated at equilibrium and distorted geometries,which satisfy

Equilibrium geometry (Q0) is optimized at MP2[64–68]/aug-cc-pVTZ[69]level using Gaussian 09.[70]The vibrational normal coordinates and vibrational frequency for the electronic ground state are calculated at MP2/aug-cc-pVTZ level and the wave functions of bound orbitals are obtained with B3LYP[71,72]/aug-cc-pVTZ using Gaussian 09 program.The frequencies of all the vibrational modes are listed in Table 1,in good agreement with the experimental data.[73]In the calculation of TDCSs,the upper limits of partial wave expansions for the bound and the continuum wave functions arelbmax=16 andlcmax=28, respectively.The Euler angle meshes for the orientation spherical average areNα=20,Nβ=16,Nγ=20,whereNα,NβandNγare the point numbers of numerical integrals for Euler angleα,βandγ.In the single-center expansion,rjranges from 0 to 8.47 a.u.with increasing step size from 0.001 a.u.to 0.128 a.u.

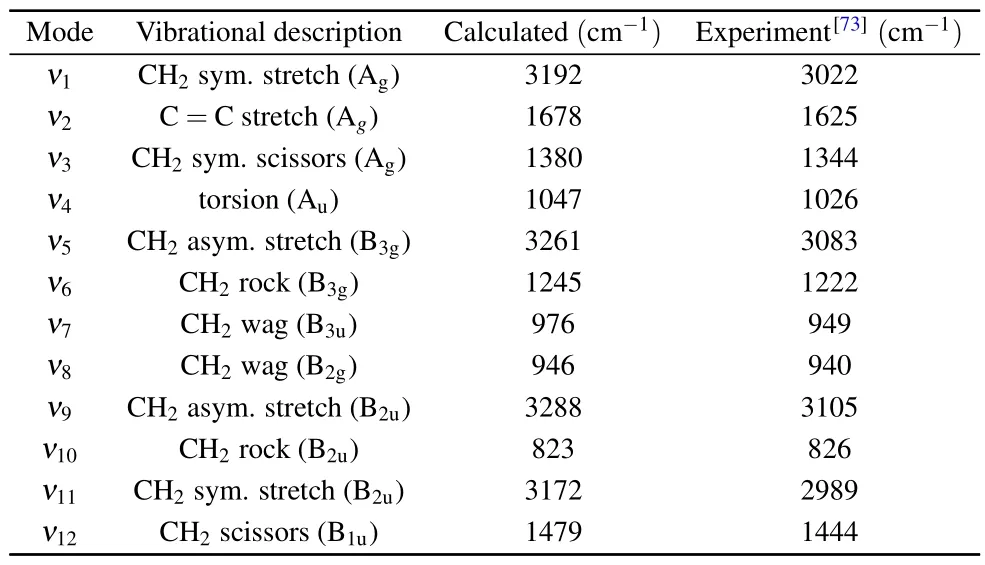
Table 1.Vibrational frequency of ethylene.

3.Results and discussion

At equilibrium geometry, ethylene molecule belongs toD2hpoint group and its ground-state electronic configuration[74]is (core)4(2ag)2(2b1u)2(1b2u)2(3ag)2(1b3g)2(1b3u)2.In the present work, the (e,2e) TDCSs of 1b3gorbital of ethylene are calculated by the MCDW method.Figure 1 shows the calculated three-dimensional(3D) angular distributions of the TDCSs for 1b3gorbital as a function of outgoing direction of the ejected electron atEi=250 eV,Ee=8 eV andθs=-10?.Figure 1(a) is the result calculated by the normal MCDW method at equilibrium geometry, and Fig.1(b) is that calculated by the v-MCDW method.In these 3D images, the magnitude of the TDCS for a given direction of ejected electron is expressed by the distance from the origin to the point on the surface.The incident electron (ki) moves along thezaxis and is scattered with a momentumksand a scattering angleθs.ki,ksas well as the momentum transfer vectorKlie in thexzplane, i.e.,the scattering plane.The binary peak along the direction of momentum transfer results from the binary collision between the incident and orbital electrons,while the recoil peak in opposite direction is regarded as the backward reflection from the residual ion of the ejected electron.Under this kinematic condition,|K|=0.754 a.u.and|ke|=0.767 a.u., which is near the Bethe ridge,the incident electron transfers almost all the changed momentum to the active bound electron.At this near the Bethe ridge kinematics,the shape of the binary peak reflects the electron momentum profile of the ionized molecular orbital.In Fig.1(a),there is an obvious dip in the direction of the momentum transfer,indicating a p-type character of the 1b3gorbital, while the intensity of the TDCS has obviously been enhanced along the momentum transfer after considering the vibrational effect,indicating that the molecular nuclear motions significantly affect the(e,2e)TDCSs.

Fig.1.Three-dimensional angular distributions of TDCSs for 1b3g orbital of ethylene molecule at Ei =250 eV, Ee =8 eV and θs =-10?calculated by (a) MCDW method at equilibrium geometry, (b) vibrational MCDW method.

Fig.2.The TDCSs for electron impact (250 eV) single ionization of 1b3g orbital of ethylene molecule in the coplanar asymmetric geometry.The ejected electron energy is displayed in each figure.Left column:θs=-6?;right column: θs=-10?.

In order to explore in detail the vibrational effect on TDCS,two typical kinematic arrangements in coplanar asymmetric geometry are investigated: 1)incident electron energyEi=250 eV with ejected electron energiesEe=8 eV,12 eV,20 eV,37 eV,74 eV and scattering anglesθs=-6?,-10?;2)incident electron energyEi=100 eV with ejected electron energiesEe=5 eV,10 eV,15 eV and scattering anglesθs=-6?,-10?.The results are plotted in Figs.2 and 3, respectively.The left column of Fig.2 shows the TDCSs in the scattering plane for(a)Ee=8 eV, (b)Ee=12 eV, (c)Ee=20 eV, (d)Ee=37 eV and(e)Ee=74 eV with scattering angle fixed atθs=-6?.The dashed blue lines represent the TDCSs calculated by the normal MCDW at equilibrium geometry, while the solid red lines represent the results calculated by the v-MCDW including molecular vibrations.The dot dashed black lines are their difference that can be regarded as the total contributions from all the vibrational modes.In Figs.2(a)–2(c),the molecular vibrations enhance the binary peaks relative to the equilibrium geometry,while for higher ejected electron energies in Figs.2(d)and 2(e),a weak negative influence can be observed.The similar behavior is also observed for scattering angleθs=-10?as shown in the right column of Fig.2.For low ejected electron energies (Ee=8 eV, 12 eV), the binary peak exhibits a double-peak structure with a dip near the direction of momentum transfer.This double-peak structure tends to merge into a single peak as the ejected electron energy increases.The binary region is strongly influenced by molecular vibrations both in shape and intensity for lower ejected electron energy and this double-peak structure becomes flattened when including vibrational motions.The recoil peaks in Fig.2,on the other hand,are not sensitive to the molecular vibrations.

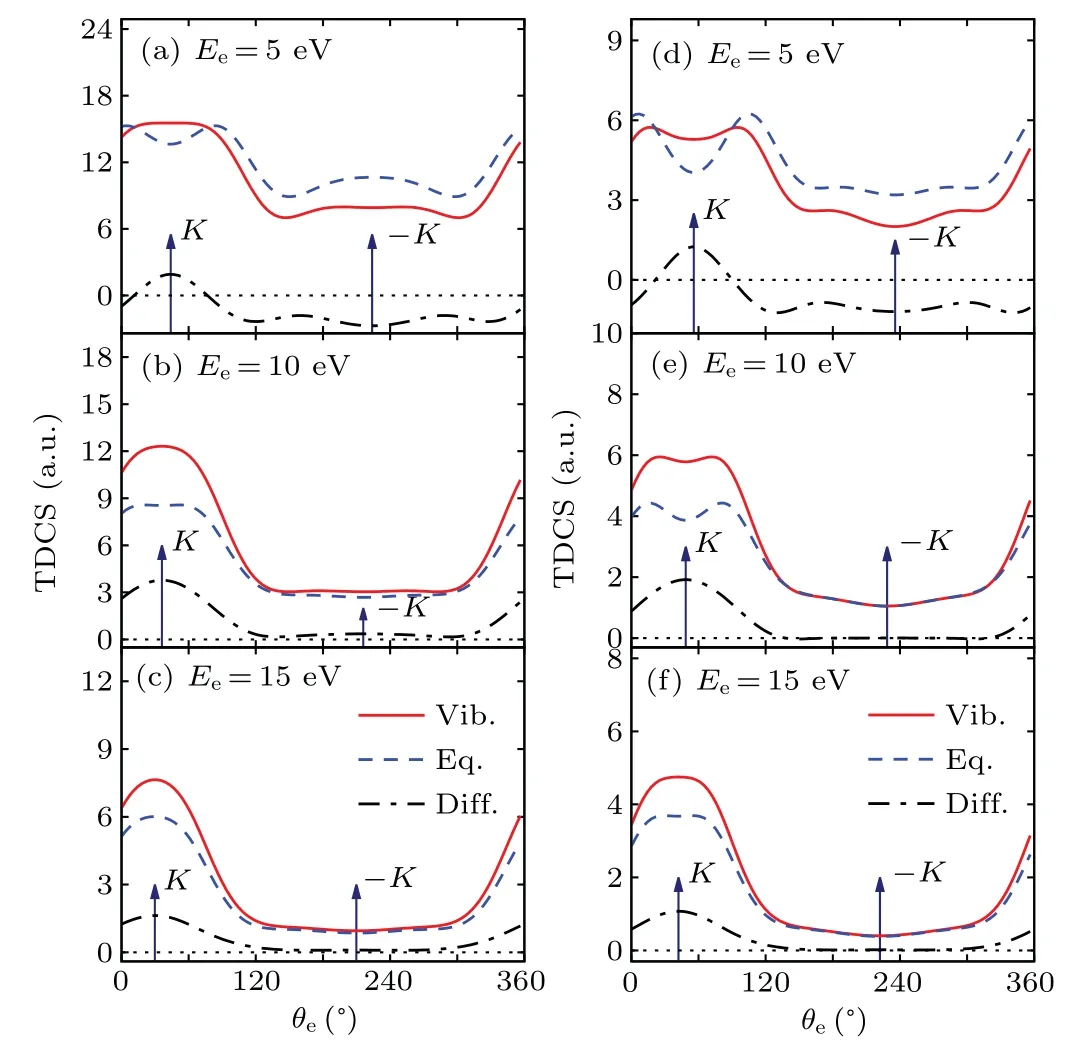
Fig.3.The TDCSs for electron impact (100 eV) single ionization of 1b3g orbital of ethylene molecule in the coplanar asymmetric geometry.The ejected electron energy is displayed in each figure.Left column:θs=-6?;right column: θs=-10?.

As we have mentioned, forEi=250 eV,Ee=8 eV andθs=-10?, which is near the Bethe ridge, the incident electron transfers almost all the changed momentum to the target electron to ensure a clean knock out.The shape of the binary peak reflects the electron momentum profile of 1b3gorbital of ethylene molecule as shown in Fig.2(f), through the relation between the ejection angleθeand the magnitude of orbital electron momentump, which can be easily obtained through the energy and momentum conservations in the ionization process.The relationship betweenpandθecan be expressed as

At Bethe ridge condition,pwill approach to 0 if the ionized electron is ejected along the direction of momentum transfer vectorK, corresponding to the center of the binary peak.In other words, the TDCS distribution near the direction ofKcharacterizes the low momentum area in the electron momentum profile of molecular orbital.From the EMS study of Watanabeet al.,[44]the 1b3gorbital of ethylene has a ptype momentum profile, having zero intensity at zero momentum (regardless of experimental momentum resolution).This leads to the deep dip in the middle of the binary peak in Figs.2(a),2(f)and 2(g).With the increase of the ejected electron energy, the kinematic condition gradually deviates from the Bethe ridge andpwill also deviate from zero at the direction ofK, therefore the double binary peak merges into a single one from Fig.2(a)to Fig.2(e)and Fig.2(f)to Fig.(j).

Figure 4 shows the contributions of individual vibrational modes on TDCS atEi=250 eV,Ee=8 eV andθs=-10?with the pictorial representations of each vibrational modes shown in the lower panel.All the twelve vibrational modes of ethylene are included in the calculations.They belong to four types of point group symmetries:D2h(ν1,ν2andν3),D2(ν4),C2h(ν5,ν6andν8), andC2v(ν7,ν9,ν10,ν11andν12).It is shown in the figure that the CH2asymmetric stretch(ν5),CH2rock(ν6),and CH2wag(ν8),which belong toC2hpoint group,have the most significant influence on the TDCS.All the vibrational modes lead to the enhanced intensity atK,resulting in the flattening of the double-peak structure for the binary peak.

Figure 3 shows the TDCSs at incident electron energyEi=100 eV withEe=5 eV, 10 eV and 15 eV and scattered angleθs=-6?,-10?.The similar behavior is observed in the binary region as in the case ofEi=250 eV.For lowest ejected electron energies(Ee=5 eV),the binary peak exhibits a double-peak structure with a dip near the momentum transfer direction.This double-peak structure tends to merge into a single peak as the ejected electron energy increases.The binary peaks are also significantly influenced by the molecular vibrations both in shape and intensity, not only enhanced but also flattened at higher ejected electron energies.As for the recoil region,the TDCSs are significantly reduced atEe=5 eV when considering vibrational motions, while the vibrational effect can be neglected for higher ejected electron energies.

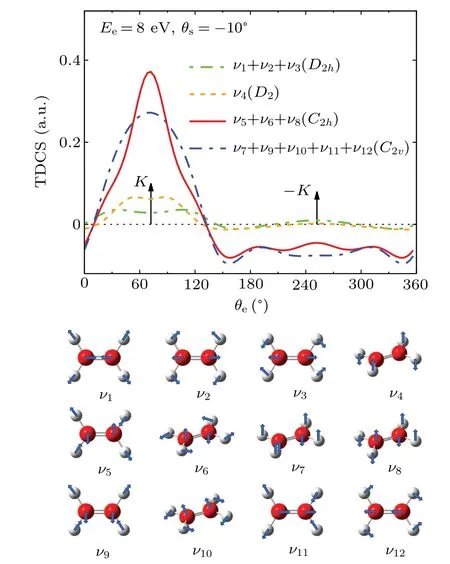
Fig.4. Contributions of all vibrational modes, which are divided by symmetry, on the TDCSs distributions of 1b3g orbital of ethylene molecule at Ee =8 eV and θs =-10?.The lower panel shows the pictorial representations of vibrational modes.

4.Summary

In summary,we have calculated the TDCSs for electronimpact single ionization from the 1b3gorbital of ethylene molecule in the coplanar asymmetric geometry at the incident electron energies of 250 eV and 100 eV using the MCDW method modified by including molecular vibrations.The results show that molecular vibrations have significant influence on the angular distributions of the TDCSs both in shape and in intensity,especially in the binary region near the Bethe ridge.The binary peak exhibits a double-peak structure with a dip along the direction of momentum transfer, which is directly related to the p-type electron momentum profile of 1b3gorbital.This double-peak structure becomes flattened when including vibrational motions in the calculation.The analysis of the contributions of individual vibrational modes shows that the CH2asymmetric stretch(ν5),CH2rock(ν6),and CH2wag(ν8), which belong toC2hpoint group, have the most significant influence on the TDCSs.The present study indicates that molecular vibration needs to be considered when we want to precisely describe the electron-impact ionization dynamics of molecules.It also suggests that molecular vibration may affect a wide range of molecular processes induced by ion collisions and photo-absorption,not only influence cross sections but may also change the dipole-forbidden transitions.

Acknowledgements

Project supported by the National Natural Science Foundation of China(Grant Nos.12004370 and 12127804)and the Strategic Priority Research Program of the Chinese Academy of Sciences(Grant No.XDB34020000).